充分利用和挖掘教材功能,指向学生的核心素养
2022-10-17常云
常 云
(江苏省南通市如皋市第二中学,江苏南通,226500)
教材是实现数学课程目标、发展学生数学学科核心素养的重要资源;教材是命题的依据,很多题目的解题的切入点都是教材上的基础知识.落实核心素养就要充分依托和发掘教材,选择合适的问题情境作为载体,突出考查核心概念、主要结论、通性通法,这对于如何进行高考备考复习,提升数学素养起很好地导向和促进作用.
1 试题源于教材,夯实基础
源题1斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
分析及解答详见人教A版普通高中教科书数学选择性必修第一册第135页例4.答案:|AB|=8,过程此处略.
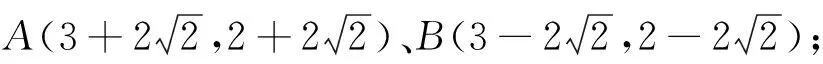
评析:本题研究直线与抛物线的位置关系考查了通性通法的使用,体现了方程思想,重视学生的分析问题和解决问题的能力,以及“数学运算”“逻辑推理”核心素养.
分析二:设A(x1,y1),B(x2,y2).由抛物线定义知,|AF|=x1+1,|BF|=x2+1,由此得|AB|=x1+x2+2,只要求出点A,B的横坐标之和x1+x2,就可以求出|AB|.
评析:本题题设中直线过焦点,有相应的结论,利用数形结合的方法求抛物线焦点弦的长|AB|=x1+x2+p.体现出(1) 转化的思想,即把求斜线段的长转化为求与坐标轴平行的线段长,转化的基础是抛物线的定义;(2) “设而不求”方法,即不需要单独求出直线与抛物线交点的横坐标x1,x2,只要整体求出x1+x2即可.
源题2过点M(2,0)作斜率为1的直线l,交抛物线y2=4x于A,B两点,求|AB|.
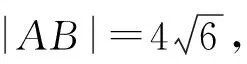

逆向思考,条件和结论互换,编拟题目
命题1已知抛物线C:y2=4x的焦点为F,斜率为1的直线l与抛物线C的交点为A,B,且|AF|+|BF|=10,求直线l的方程.
分析:设直线l:y=x+t,则与抛物线C方程联立得x2+2(t-2)x+t2=0,用母题分析二的结论|AF|+|BF|=x1+x2+2及已知建立关于t方程求解即可.
命题“源于教材,高于教材”. “高”在逆向思考,直线l并不过抛物线的焦点,以直线的纵截距为参数,渗透方程思想.尽管如此,求解方法、思想根植于教材.
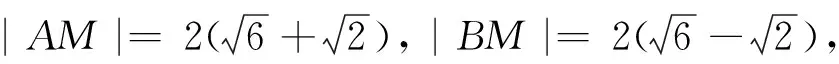
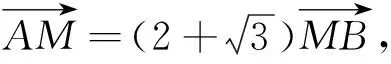


命题专家在A,M,B三点共线上精心设计,不落俗套,又把根与系数的关系内隐于题设的条件之中,“于无声处听惊雷”,两者巧妙地结合起来建立关于y2的方程是破题的关键,使理性思维、逻辑推理和数学运算充分结合起来,达到预期的目的.
高考命题“题在书外,但根在书里”,为了突出综合性,将几个母题经过加工改造,编拟为一个题,使得特殊性在外而普遍性在内.一旦问题的特殊性被发现,命题突破口就找到了,平和中适度彰显创新性、综合性与实践性,以体现高考的选拔功能与导向作用.
2 试题展示

(1) 若|AF|+|BF|=4,求l的方程;
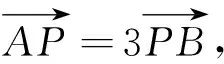
3 多视角探究,落实素养






点评:直线与抛物线的位置关系,一般要用到根与系数的关系,消元,“设而不求”“整体代入”.有关弦长问题,要注意是否过抛物线的焦点.若过抛物线的焦点,则可直接使用公式|AB|=x1+x2+p,若不过焦点,则必须用一般弦长公式.
4 变式探究,提升应变能力
变式:已知抛物线C:y2=2px(p>0)的焦点为F,A(x1,y1),B(x2,y2)是该抛物线上位于x轴两侧的点,且|AF|+|BF|=4.
(1) 求该抛物线的方程;
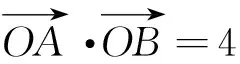



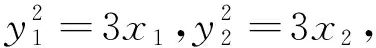

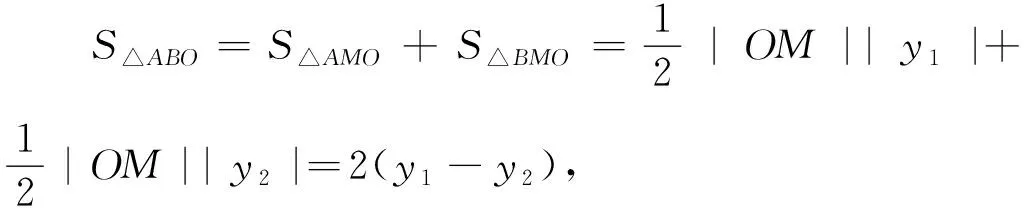

评注:本题第(1)小题如果不过焦点,则纵坐标关系更简单,故考虑横截式方程.充分利用抛物线弦长公式和方程思想,采用“设而不求”的方法即可;第(2)小题以平面向量数量积为抓手,转化为以y1y2为变元的方程,再用根与系数关系得到直线与x轴的交点,最后把△ABO与△AFO面积之和表示为关于y1的函数,用基本不等式求解即可,试题一经这样的变式同样考查了“四基”和“四能”.
变式教学着眼于学生的基础,在学生的 “最近发展区”逐步拓展,最终达到《考试大纲》《考试说明》所要求的高度,与高考试题充分的对接,这也是避免“教材题简单不足以应对高考”的最好例证,也是避免学生在“题海”中增加负担的最有效方式.基于教材,能在教材中找到影子,真正发挥教材的示范引领与育人功能.
5 反思总结
高考数学复习,应该立足教材.教师需要读懂教材,根植教材,选择典型例习题进行加工改造,把基础题编拟成具有多向考点的中档综合题;还要充实教材,进行一题多变,多题一法的变式教学,用教材最少的资源获取最大的功利,而不是在题海中增加学生的负担.因此,教学中教师要做到狠下功夫,钻研教材,精心设计,回归课堂,用好教材,通过设计变式题,注重“在知识网络交汇处命题”来培养学生的思维能力与创新意识,提高学生知识迁移能力、综合分析能力,发展学生的核心素养.
解析法是用代数方法研究几何问题的方法,其操作步骤是程序化的,关键在于几何条件代数化(坐标化),其关系式的简洁程度和处理的容易程度就是解析几何的精妙所在.
直线与抛物线的位置关系,属于每年必考的内容之一.重视学科的主干知识,围绕主干内容加强学生对基本概念、基本思想方法的理解和关键能力的培养仍然是教学的着力点和目标.立德树人不仅仅在书面上、口头上,而且要落实在实际行动上,用自己的行为去感化学生、激励学生去学会数学、研究数学,更好地形成终身学习的能力和意识.
