脉冲参数对CFST拱桥地震反应的影响

李子奇，李亮亮，王 力，王宇翰

(兰州交通大学 土木工程学院,甘肃 兰州 730070)

0 引言

近年来，大跨度CFST拱桥因跨越能力大、节省材料和较短的建设周期等优点在我国铁路桥梁工程得到了快速的发展和应用。但由于近断层脉冲型地震记录较少，脉冲参数对CFST拱桥的地震反应的研究还不够深入。发生过的汶川地震、熊本地震、花莲地震、青海玛多地震等地震记录都表现出了明显的近断层脉冲型地震动特性，因此，大量的学者开始关注脉冲型地震动对中长周期结构的反应。对于大跨CFST拱桥此类中长周期结构，拱肋和桥墩作为其的主要抗力构件，研究脉冲参数对CFST拱桥地震反应的影响是目前很少关注的1个问题。

目前，脉冲型地震动和CFST拱桥地震反应的研究方面国内外学者已经取得一些有益的成果。关于近断层地震特性研究领域，贾俊峰等[1]总结了前方向性效应、滑冲效应、上盘效应和竖向地面运动等近断层地震动特点，概括了近断裂带水平和竖向地震作用下结构地震响应的研究进展。Zamora等[2]基于弹性和非弹性反应谱，发现近断层脉冲样、近断层非脉冲样和远场地震动对结构响应有明显差异。近断层地震识别与分类方面，Zhai等[3]提出1种基于能量的方法识别速度脉冲地震动。赵天次等[4]提出利用连续小波变换识别3个正交分量地震记录中能量最大的速度脉冲方向。Hayden等[5]从太平洋地震中心提取大量地震波分类为不同脉冲周期的近断层脉冲运动，并进一步细分了由前方向效应引起的脉冲运动。关于近断层地震动信号模拟方面，Whitney[6]基于莫尔斯小波建立了1个合成脉冲的模型，合成脉冲模型可以用于补充并模拟可用的地面运动数据库。Wu等[7]提出了1种将修正的统计格林函数和理论格林函数相结合的方法对近断层时程进行数值模拟，可考虑地震时地面永久位移。田玉基等[8]采用1种连续三角函数方法可模拟不同地震动参数的脉冲成分。

大跨度CFST拱桥地震响应方面，Chen等[9]对CFST拱桥进行随机地震分析结果表明，较软的场地条件可以放大结构响应，应考虑地震动输入维数和垂直地震动的影响。邢帆等[10]等研究了近断层地震对飞鸟式CFST拱桥响应，认为地震动的卓越频率接近于基本周期不一定会造成中长周期的大跨结构的破坏。徐略勤等[11]以近断层地震动作为激励，开展了全桥地震响应分析，研究结果表明近断层地震动对拱肋和风撑地震内力的不利影响最大。李晰等[12]等的研究结论表明有无脉冲、脉冲周期、地震动输入维数以及桥梁修建处场地都对CFST拱桥地震响应有较大影响。邹建豪等[13]对CFST拱桥进行地震分析发现纵、竖向位移主要由纵向激励引起，横向位移则主要由横向激励引起。Xin等[14]考虑滑冲效应对1座中承式大跨度CFST拱桥进行分析，研究结果表明滑冲运动由静态和动态脉冲组成，两者对结构地震反应和性能状态均具有重要影响。Xing等[15]以1座大跨度CFST拱桥为背景,发现滑冲效应对长周期拱桥的损伤大于方向性效应。段昕智等[16]的研究结果表明滑冲效应在长周期CFST拱桥产生较大位移及内力响应，加速度脉冲对桥梁内力影响较大。

已有研究主要存在2个问题：1)以往研究多集中在天然地震动对结构地震反应方面，而天然地震记录样本不足，缺乏不同脉冲参数的地震记录；2)在强震作用下不同脉冲参数对大跨度CFST拱肋及边墩地震反应方面研究较少。

基于此，本文以一大跨度CFST拱桥为背景，人工构造同一PGA下，不同脉冲幅值、脉冲周期、脉冲个数的人工近断层地震记录，对其进行非线性时程分析。探究同一PGA下不同脉冲参数对拱肋及桥墩地震反应影响规律。研究结果可为CFST拱桥近断裂带抗震设计提供参考依据。

1 工程实例

该桥采用一跨过江方案，主跨为430 m中承式CFST拱桥，全桥主梁为5跨一联的预应力混凝土连续梁，孔跨布置为39.6 m+32 m+384 m+28 m+34.6 m连续梁，桥梁结构体系采用半漂浮体系，如图1所示。

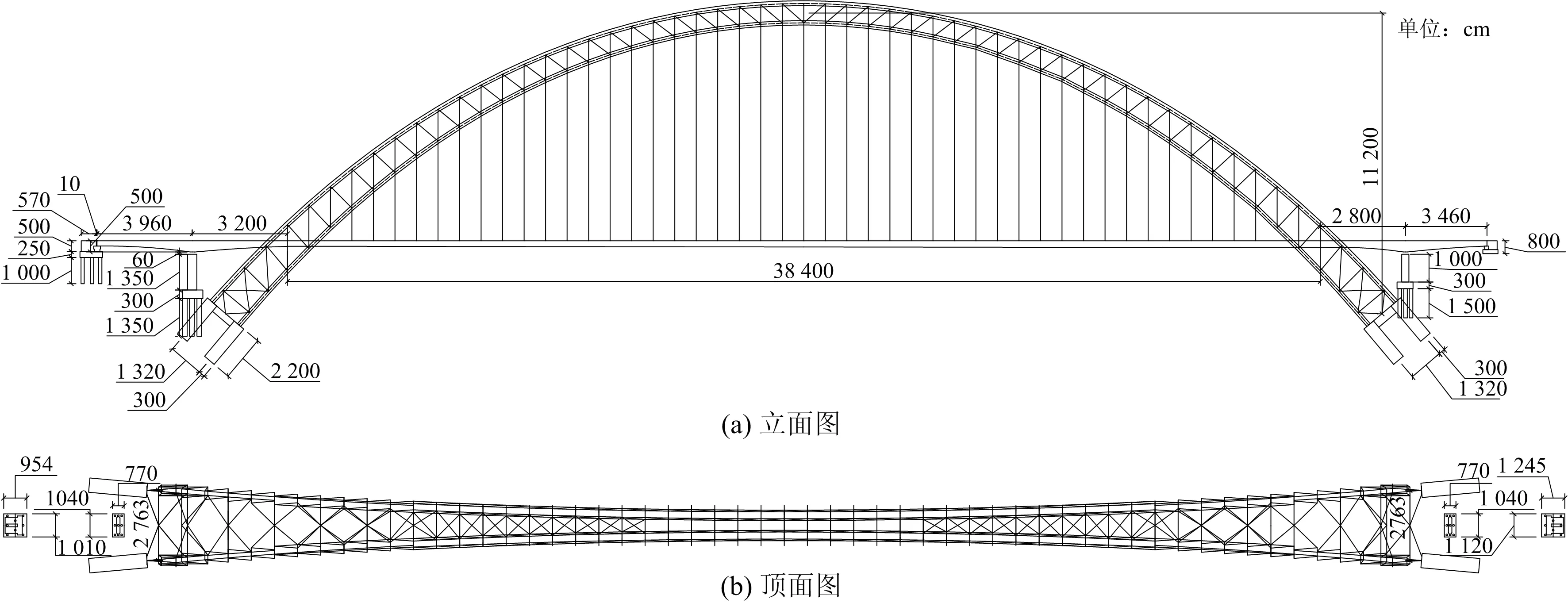
图1 藏木特大桥总体布置Fig.1 General layout of Zangmu Bridge

2 有限元模型及结构动力特性分析

通过有限元软件CSI Bridge建立该桥的三维非线性模型如图2所示，主梁采用C55混凝土弹性梁柱单元建立，吊杆采用桁架单元建立。钢管混凝土拱肋采用钢-混凝土组合截面纤维截面单元模拟如图3所示，能较好地考虑动轴力对拱肋的非线性行为的影响。以同样的方式，边墩也通过非线性纤维截面单元建立，模拟桥墩的非线性行为。假设桥梁位于在刚性基础上，拱脚底部和桥墩底部均采用固定端约束，桥台也采用理想固定端约束。桥梁结构建模过程中考虑结构的自重、二期荷载、吊杆初拉力作用。由于《铁路工程抗震设计规范》(GB 50111—2006)[17]对时程分析时结构阻尼比无说明，依据《公路桥梁抗震设计规范》(JTG/T 2231-01—2022)[18]6.2.2规定：组合结构阻尼比可取5%，故CFST拱桥时程分析时采用阻尼比为5%的瑞利阻尼。

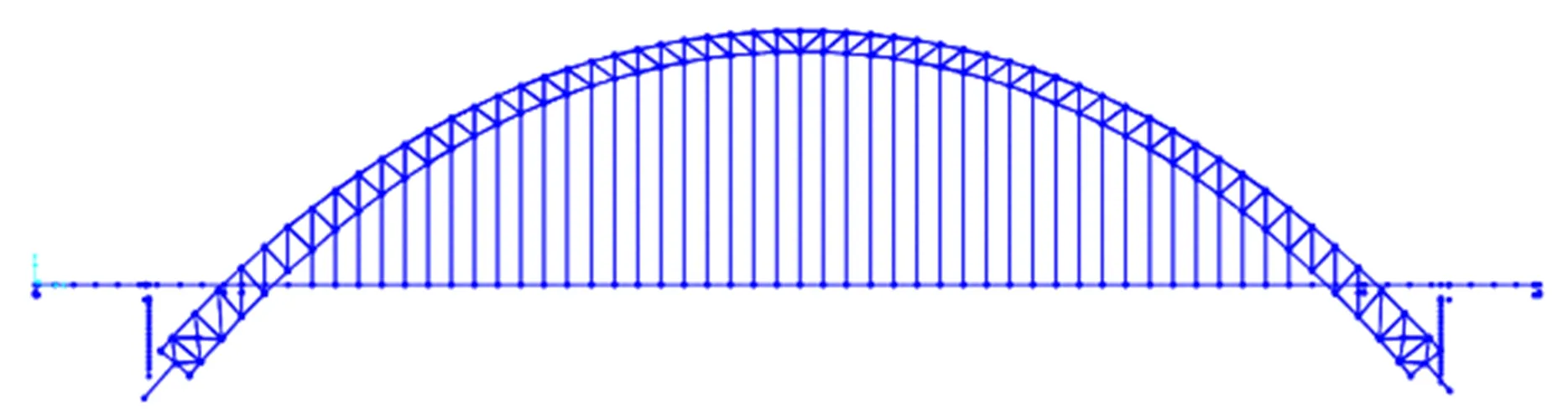
图2 全桥有限元模型示意Fig.2 Schematic diagram for finite element model of whole bridge

图3 拱肋及墩底纤维截面划分Fig.3 Division of arch ribs and pier bottom fiber sections

对CFST拱桥进行结构动力特性分析，CFST拱桥的自振周期和振型形状由表1所示。

表1 结构动力特性计算结果Table 1 Calculation results of structural dynamic characteristics

由表1计算结果可知：1)大跨度CFST拱桥属于中长周期结构，该结构柔度较大；2)该结构低阶振型为横向振型，一阶振型为主梁横向振动，二阶振型为拱肋横向振动，拱肋刚度大于主梁刚度；3)该结构振型形状在顺桥向及竖向振动受高阶振型影响显著，横桥向振动时受低阶振型影响显著，该结构面外刚度小于面内刚度。

3 人工近断层地震记录的构造

本文采用田玉基模型，采用文献[19]方法合成人工地震记录，高频成分由调幅后的天然地震动模拟，低频成分由人工构造不同幅值、脉冲周期、脉冲个数主脉冲模拟，然后合成罕遇地震水准0.408 g的人工近断层地震记录。

人工近断层地震高频成分由天然地震动模拟，选取PGV/PGA<0.2，断层距>70 km的远场无脉冲型地震记录。从太平洋地震数据库中选择Trinidad地震事件，台站和分量为TRINIDAD.B_B～RDW～000的天然地震记录。该地震记录PGA=151 cm/s2、PGV=8.9 cm/s、PGV/PGA=0.06。

人工近断层地震低频成分由等效脉冲模型模拟，田玉基速度脉冲模型如式(1)所示：

V(t)=Vp·ω(t)·cos[2πfp(t-t1)] 0≤t≤T

(1)

式中：Vp是速度脉冲峰值，cm/s；fp是速度脉冲的频率，Hz；t1是速度脉冲相位角相关参数，s；T是速度时程的持续时间，s。

速度时程的包络函数如式(2)所示：

(2)

式中：γ是脉冲形状参数；t0是包络函数峰值发生时刻，s。

以脉冲幅值、脉冲周期，脉冲个数作为单参数变量，利用EQ Signal程序[20-21]生成不同脉冲参数的人工脉冲地震记录如图4～6所示，脉冲参数取值见表2。对于大跨度复杂的拱式结构，需考虑竖向地震动，地震动输入方式为三向输入，桥梁纵向、横向及竖向按1∶0.85∶0.65输入。

图4 不同脉冲幅值速度时程Fig.4 Velocity time history for different pulse amplitude

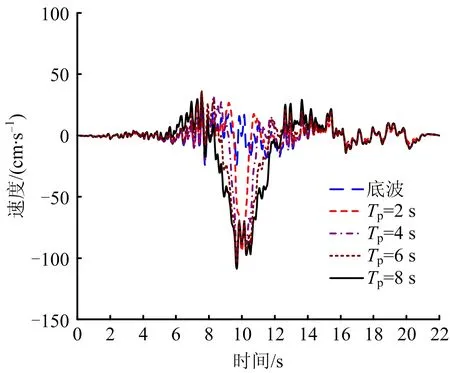
图5 不同脉冲周期速度时程Fig.5 Velocity time history for different pulse period

图6 不同脉冲个数速度时程Fig.6 Velocity time history with different number of pulse

表2 脉冲参数取值Table 2 Values of pulse parameters

4 脉冲参数对拱桥地震反应的影响

对于不同地震动特性的地震记录作用下，拱脚处及梁拱交界处地震反应差异较为显著且拱肋下弦杆内力较大。因此，选取拱顶、小里程侧拱脚下弦杆、小里程侧梁拱交界处下弦杆及小里程侧墩底截面分析拱桥地震反应。因为该结构横向地震作用较为显著，限于篇幅只分析拱肋横向地震反应，桥墩纵向地震反应。

脉冲参数对拱肋横向地震反应的影响如图7～9所示。

图7 脉冲幅值对拱肋地震反应Fig.7 Seismic response of pulse amplitude to arch ribs

图8 脉冲周期对拱肋地震反应Fig.8 Influence of pulse period on seismic response of arch rib

图9 脉冲个数对拱肋地震反应Fig.9 Influence of the number of pulses on the seismic response of arch rib

由图7可知：同一PGA下，速度脉冲幅值越大，拱肋内力及位移反应越大，二者近似呈线性关系。脉冲幅值50 cm/s时，低频脉冲成分对拱顶位移贡献率为76%(脉冲成分对地震反应贡献率计算方法为：脉冲成分反应=合成的有脉冲波反应-底波反应，可近似表征脉冲成分对结构响应的影响)，对拱脚轴力贡献率为17%；脉冲幅值200 cm/s时，脉冲成分对拱顶位移贡献率为92%，对拱脚轴力贡献率为40%。由此可见，拱顶位移主要由脉冲成分控制，随着脉冲幅值增高，脉冲成分对拱肋内力及位移影响愈加显著。出现这种现象的原因可能是脉冲幅值越大，其反应谱中长周期谱值较大，激起更大的拱肋横向振动，使拱肋产生较大内力及位移。

如图8所示，同一PGA下，在脉冲周期0～8 s内，拱顶位移、拱脚轴力，梁拱交界处弯矩呈现先增大后减小的规律，在脉冲周期2～6 s范围内，地震反应较大。拱脚弯矩随脉冲周期变化而增大。脉冲周期为4 s时，拱顶位移达90 cm，9倍于无脉冲地震动产生的位移，下弦杆拱脚轴力达202 500 kN，比无脉冲地震动产生拱脚轴力增大33%。出现这种现象可能是地震波速度脉冲周期2～6 s范围内，接近结构的一阶周期(5.2 s)及二阶周期(3.12 s)，易激发结构低阶振型，加剧拱肋的地震反应。

如图9所示，同一PGA下，速度脉冲个数越多，拱肋横向内力及位移反应越大。单脉冲成分对拱顶位移贡献率为88%，双向脉冲成分对拱顶位移贡献率为92%，多脉冲成分对拱顶位移贡献率为93%；单脉冲成分对拱脚轴力贡献率为29%，双向脉冲成分对拱脚轴力贡献率为35%，多脉冲成分对拱脚轴力贡献率为29%。出现这种规律可能是因为脉冲个数越多，其反应谱中长周期谱值越大，且中长周期谱值峰值对应的周期也越大，蕴含更多的低频成分能量，对于较柔的结构体系，能激起更大的拱肋横向振动，使拱肋产生较大内力位移反应。

脉冲参数对桥墩纵向地震反应的影响如图10～13所示。

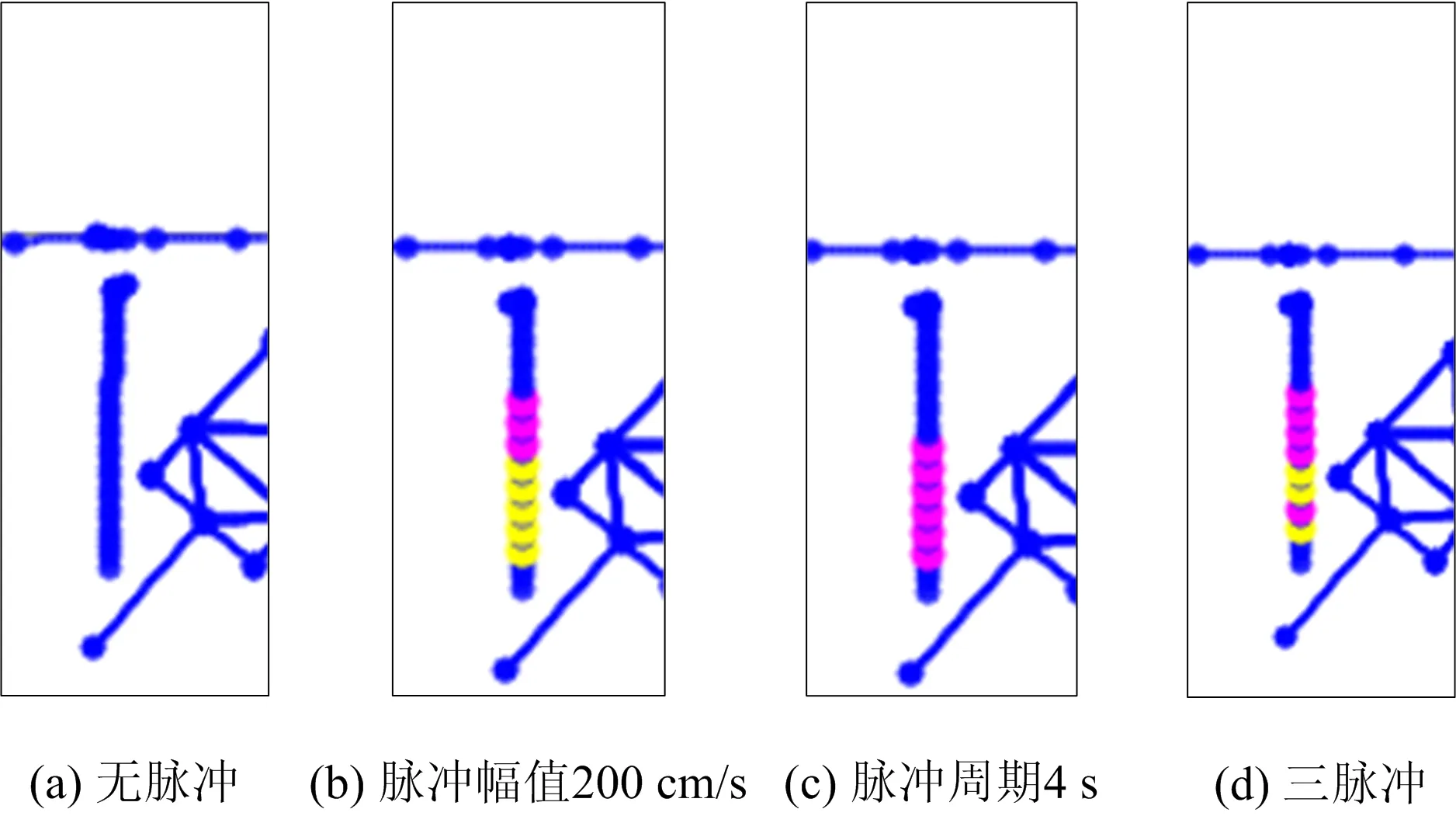
注：CSI Bridge中粉色铰代表屈服，黄色铰代表达到极限承载能力图10 桥墩屈服状态Fig.10 Yield state of pier

图11 脉冲幅值纵向弯矩-转角曲线Fig.11 Influence of pulse amplitude on longitudinal bending moment-rotation angle

图12 脉冲周期纵向弯矩-转角曲线Fig.12 Influence of pulse period on longitudinal bending moment-rotation angle

图13 脉冲个数纵向弯矩-转角曲线Fig.13 Effect of pulse number on longitudinal bending moment-rotation angle

CFST拱桥桥墩纵向地震响应较为显著，地震激励时纵向墩底塑性转角远远大于横向，因此，选择纵向地震响应来分析桥墩反应。

在三向罕遇水准地震作用下，CFST拱桥拱肋均处于弹性状态，未发生屈服现象，拱肋抗震性能优良，桥墩发生了不同状态的屈服破坏现象，如图10所示：无脉冲时桥墩处于弹性状态；脉冲幅值为200 cm/s时，墩底至1/2墩高处发生屈服，墩底部分单元达到极限承载力；脉冲周期为4 s时，墩底至1/2墩高处发生屈服；三脉冲时，墩底至1/2墩高处发生屈服，墩底部分单元达到极限承载力。

不同脉冲参数地震动作用时，墩底纵向弯矩-转角曲线如图11～图13所示。

如图11所示，随着脉冲幅值增大，墩底纵向塑性转角不断增大，无脉冲时墩底处于弹性状态，脉冲幅值高于50 cm/s墩底进入塑性状态。随着脉冲幅值的增大，墩底塑性变形不断增大，桥墩损伤程度也不断增加。

如图12所示，随着脉冲周期的变化，墩底纵向塑性转角在脉冲周期为2～4 s时最大，达0.000 3 rad。脉冲周期在2～4 s时，桥墩损伤程度最为严重。

如图13所示，双向脉冲和三脉冲地震记录作用下桥墩纵向产生较大塑性转角，随脉冲个数的增多，桥墩损伤程度也不断增加。

由图10～13可知，对于近断层脉冲型地震动，即使PGA相同，不同脉冲参数的地震动对CFST拱桥桥墩的损伤状态差异较大。近断裂带附近大跨度桥梁选用PGA作为强度指标进行地震验算有较大局限性，应综合考虑地震动脉冲参数进行地震验算。

5 结论

1)同等PGA时，脉冲幅值越大,脉冲成分对拱肋内力及位移反应贡献越大，二者近似呈线性关系。

2)同等PGA时，在脉冲周期0～8 s内，拱顶位移、拱脚轴力，梁拱交界处弯矩呈现先增大后减小的规律，脉冲周期约4 s时拱肋地震反应达到峰值。在脉冲周期2～6 s范围内，易激起结构低阶振型，使拱桥产生较大地震反应。

3)同等PGA时，速度脉冲个数越多，蕴含更多低频成分地震能量，脉冲成分对拱肋内力及位移反应贡献越大。

4)对于大跨度CFST拱桥，三向罕遇地震作用下，拱肋处于弹性状态，桥墩可能屈服。随着脉冲幅值的增大，脉冲个数的增多，墩底塑性转角不断增大。脉冲周期在2～4 s时，桥墩损伤程度最为严重。

5)近断裂带附近大跨度桥梁选用PGA作为强度指标进行地震验算有较大局限性，应综合考虑近断层地震动脉冲参数进行地震验算。