基于PCA-BBO-SVM的尾矿坝变形预测模型与性能验证研究*

华国威，娄彦彬，王世杰，胡少华,3

(1.武汉理工大学 安全科学与应急管理学院，湖北 武汉 430070；2.河南省电力勘测设计院,河南 郑州 450007;3.国家大坝安全工程技术研究中心，湖北 武汉 430010)

0 引言

尾矿坝每时每刻都处于变形状态，一定程度的变形属于正常现象，超过阈值会导致溃坝。因此，利用已有尾矿坝历史监测数据，寻找有效的数学模型对尾矿坝变形进行预测预报，对尾矿坝的安全稳定运行具有重要意义[1]。

目前，常见预测模型有统计模型、BP神经网络、支持向量机(SVM)等，传统统计模型无法准确描述尾矿坝复杂的非线性变形规律；BP神经网络的预测精度受初值影响，收敛速度慢且易陷入局部最优解[2]。而SVM模型具有强大的非线性数据处理能力，泛化能力强，预测精度高[3]，可用于尾矿坝的变形预测。

在实际工程应用中，参数的选择直接影响SVM模型的预测性能，目前对SVM参数寻优的方法主要有网格搜索法(GS)、遗传算法(GA)、粒子群算法(PSO)等[4]，但GS寻优效率低，GA和PSO易陷入局部最优解。生物地理学优化算法(BBO)具有参数简单、寻优范围大、收敛速度快、不易陷入局部最优的特性，可用来对SVM参数进行寻优，提高模型性能。

在选取尾矿坝变形影响因子时，由于各因子间存在一定相关性，将所有因子输入会造成信息冗余，影响模型预测结果。为此，本文利用PCA优选出尾矿坝变形的主要影响因子作为输入量，引入BBO算法对SVM参数进行寻优，从而提升模型的预测性能，并结合工程实例与BP、GS-SVM、GA-SVM、PSO-SVM模型进行对比，验证模型性能。

1 尾矿坝变形预测模型构建

1.1 尾矿坝变形影响因素分析

尾矿坝变形由复杂反应综合导致，具有非线性特性。一方面由于坝体自身状态(筑坝方式、时间引起的徐变等)使坝体表现出宏观变形趋势;另一方面受环境因素(库水位、温度、浸润线、干滩、降雨量等)影响，使其变形数据表现出周期性和随机波动性[5-8]。一般尾矿坝变形主要影响因子包括：库水位(H，H2，H3)；温度因子(sin(T)，cos(T))，其中T=sin(2πt/365)；时效因子(θ，lnθ)，其中θ=t/100，t为尾矿坝建立到监测日的累积时长；浸润线长度、干滩长度以及降雨量。

由于各影响因子间存在一定相关性，直接输入会使预测模型产生过拟合现象，因此，需要对监测数据进行优选，选出最具代表性的输入量。

1.2 基于PCA的尾矿坝变形影响因子优选

PCA是多元统计学中用于检验变量内部相关性的方法[9]，本文利用PCA优选尾矿坝变形影响因子作为预测模型的输入数据。PCA优选包括以下6个步骤：

1)输入尾矿坝变形量和影响因子的监测数据，形成原始数据矩阵X，如式(1)所示：

X=[Xij]n×p

(1)

式中：n代表样本总数；前p-1列代表尾矿坝变形影响因子；第p列代表尾矿坝变形量。

2)利用Z-Score法对变形影响因子进行归一化处理，得到新的数据矩阵S。

3)计算矩阵S的协方差矩阵C,并求C的特征值λ及特征向量u，如式(2)～(3)所示：

C=cov(S)

(2)

Cu=λu

(3)

4)将原始影响因子数据投影到特征向量u上，得到主成分y如式(4)所示：

y=uTXT

(4)

5)计算前k个主成分的累积贡献率α，如式(5)所示：

(5)

6)选取累积贡献率大于85%的前k个主成分,将与各主成分相关性高的尾矿坝变形影响因子作为预测模型输入量。

1.3 BBO优化SVM的尾矿坝变形预测模型

SVM在多维数、非线性问题的处理上具有独特优势[10]，可用来描述尾矿坝变形数据与变形影响因子之间的复杂映射关系。核函数是SVM处理非线性函数的核心，本文核函数选取径向基函数(RBF)如式(6)所示：

(6)

式中：k(x,xi)为核函数；g为核函数参数；x,xi均为输入量。

在实际运行过程中SVM模型预测精度由惩罚因子C和核函数参数g共同决定[11]，因此选择合适的参数寻优算法可直接影响模型性能和稳定性。

本文选择BBO算法对SVM参数进行寻优，BBO算法通过模拟大自然间物种迁移变异规律，具有参数简单、收敛速度快、不易陷入局部最优的特点[12-13]，迁移和变异是BBO算法的核心操作。

1)迁移操作。本文选用余弦迁移模型，如图1所示。其中，λ为迁入率，μ为迁出率，I为最大迁入率，E为最大迁出率，Smax为最大物种数量。

图1 物种迁移模型Fig.1 Species migration model

2)变异操作。物种变异计算如式(7)所示：

(7)

式中：gs指物种变异概率；gmax为最大变异率；ps表示生物数量为s时的概率；pmax为ps的最大值。

本文将平均均方根误差R作为BBO算法的优化目标，如式(8)所示：

(8)

图2为PCA-BBO-SVM预测模型流程。

图2 PCA-BBO-SVM预测模型流程Fig.2 Flow chart of PCA-BBO-SVM prediction model

2 工程实例

2.1 工程概况

以杨家湾尾矿坝变形量为预测对象，建立变形预测模型。该尾矿坝采用上游式筑坝方式，初期坝为透水堆石坝，坝高17.4 m，坝长146.45 m，坝顶宽5 m。选择同一横线上4个测点GA-2，GB-3，GD-4，GF-3的历史监测数据进行预测，浸润线数据选用A-3，B-3，C-4，G-3，浸润线A、B、C、G间距为15.68，29.60，74.36 m，各测点与浸润线距离如图3所示。

图3 位移测点与浸润线平面示意Fig.3 Plan view of displacement measuring points and saturation lines

2.2 数据预处理

尾矿坝监测数据中存在大量噪声，因此利用小波对尾矿坝变形数据进行去噪，再利用PCA对影响因子进行优选。各主成分贡献率及累积贡献率如图4所示。由图4可知，前4个主成分可以用来描述原始数据信息，各点前4个主成分原始数据特征向量见表1。绝对值越大代表该因子与主成分相关性越大[14]，由表1可知，各主成分主要特征向量绝对值均大于0.4。本文优选出的输入量为库水位(H，H2，H3)、温度因子(sin(T)，cos(T))、时效因子(θ，lnθ)、浸润线长度以及干滩长度。

表1 前4个主成分的特征向量Table 1 Feature vectors of first four principal components

图4 贡献率与累积贡献率Fig.4 Contribution rate and cumulative contribution rate

2.3 模型预测及性能验证

BBO算法寻优前需要设置参数，参考文献[15-16]并经过多次模拟实验调整得到具体参数：Smax=50,I=1，E=1，qmax=0.05，栖息地保持率L=0.2，迭代次数D=100，BBO算法的寻优范围为[0.001,1000]。本文选择均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)对模型性能进行评价，如式(9)～(11)所示：

(9)

(10)

(11)

引入BP、GS-SVM、PSO-SVM、GA-SVM模型与PCA-BBO-SVM模型进行对比，验证可得PCA-BBO-SVM模型性能更优。以上模型各测点的预测对比如图5所示。由图5可知，由于预测时间不同，导致尾矿坝变形趋势不同。BP模型预测性能最差，波动预测能力和预测精度均无法达到预计效果，仅能预测变形总趋势，与监测值偏差和GS-SVM模型相似；GS-SVM模型预测的走向基本与实测值相吻合，但该模型并不能精确预测局部细节波动，得出的模型不够稳定，GS-SVM模型与实测值之间的偏差仍然过大；GA-SVM和PSO-SVM模型整体预测效果优于GS-SVM模型，可以预测部分波动点，预测精度得到进一步提升，但仍有部分波峰波谷无法精确预测；PCA-BBO-SVM模型性能在所有模型中最优，能够更准确地预测变形监测数据中的波峰波谷，同时其预测数据更贴近实际监测数据，误差值小。

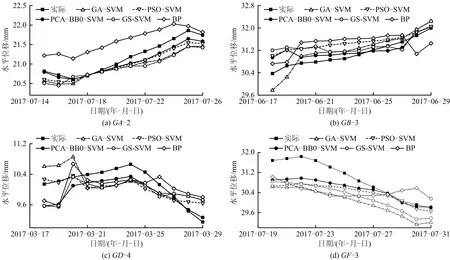
图5 不同模型在不同测点变形预测性能对比Fig.5 Comparison on deformation prediction performance of different models at different measuring points

各模型性能指标如表2所示。由表2可知，4个测点PCA-BBO-SVM模型的RMSE指标分别为0.139 6，0.274 2，0.317 0，0.530 6，MAE指标分别为0.112 5，0.213 5，0.269 0，0.412 9，优于其他模型；GA-SVM、PSO-SVM、GS-SVM模型指标大小相似，其中PSO-SVM模型略优，BP模型相对最大。说明PCA-BBO-SVM模型的实际误差相对最小，模型更加稳定，通过GS、GA以及PSO寻优的SVM模型次之，BP模型误差最大。4个测点中PCA-BBO-SVM模型的MAPE分别为0.525 0%，0.692 3%，2.621 2%，1.311 2%，可以看出PCA-BBO-SVM模型预测数据贴近实测数据，精度足够高，可用于尾矿坝变形预测。

由图5和表2可知，BP模型预测精度与GS-SVM模型相似，但对变形趋势的预测能力弱于GS-SVM模型；GS-SVM模型能够大致预测变形的整体趋势，但模型精度以及对波峰波谷预测能力不足；由于GA和PSO算法的寻优范围及速度均大于GS算法，参数选择更优，因此GA-SVM和PSO-SVM模型大部分测点预测精度及波峰波谷的预测性能优于GS-SVM模型，但由于GA与PSO算法易于陷入局部最优解，仍有个别测点预测性能弱于GS-SVM模型；PCA-BBO-SVM模型由于BBO算法不易陷入最优解，可以设置更大的寻优范围，能获得更为准确的参数C和g，使其对局部细节趋势的预测能力比GS-SVM模型、GA-SVM模型和PSO-SVM模型更完美，能够更为完美地预测数据的波峰波谷，且该模型的预测数据足够贴近真实数据，因此PCA-BBO-SVM模型适用于尾矿坝的变形预测。

表2 不同测点各模型变形预测精度统计Table 2 Statistics on deformation prediction accuracy of each model at different measuring points

3 结论

1)将PCA优选出的尾矿坝变形影响因子作为预测输入量，并利用BBO算法参数简单、不易陷入局部最优解的优点，对SVM参数进行寻优，建立基于PCA-BBO-SVM的尾矿坝变形预测模型。

2)通过利用PCA-BBO-SVM模型对尾矿坝4个监测点变形数据进行预测，均方根误差分别为0.139 6，0.274 2，0.317 0，0.530 6，平均绝对误差分别为0.112 5，0.213 5，0.269 0，0.412 9,平均绝对百分比误差为0.525 0%，0.692 3%，2.621 2%，1.311 2%。

3)提出的PCA-BBO-SVM尾矿坝变形预测模型的预测精度、整体趋势预测能力及细节波动预测性能优于BP、GS-SVM、GA-SVM、PSO-SVM模型，且预测数据足够贴近实测数据，研究结果可为尾矿安全监测提供参考，具有工程实用性。