改进差分进化算法及啤酒灌装机液位控制PID参数整定
2022-10-17王超锋司呈勇沈建强
王超锋,司呈勇,,沈建强
改进差分进化算法及啤酒灌装机液位控制PID参数整定
王超锋a,司呈勇a,b,沈建强b
(上海理工大学 a.光电信息与计算机工程学院 b.中德国际学院,上海 200093)
针对啤酒液位控制系统存在PID参数整定难、非线性、滞后性问题,提出一种改进基于邻域的改进差分进化算法,应用于PID参数优化整定中,从而提高灌装机的工作效率和啤酒的质量。文中对差分进化算法进行改进,设计一种新型的变异策略,在变异环节引入邻域搜索操作;根据当前种群的分布情况,实时对邻域的个数进行自适应分配,以提升算法全局和局部搜索能力;与2种基本差分进化算法和4种改进差分进化算法对比,用18个测试函数验证文中所提出算法的性能。仿真结果表明,相较于基本差分进化算法,使用改进的差分进化算法整定的PID参数,调节时间减少0.22 s,上升时间减少0.04 s,超调量降低7.63%。通过改进的差分进化算法对啤酒灌装机液位PID参数的优化整定,可以显著改善控制系统的超调量、上升时间和稳态误差等性能,实现了液位的稳定控制。
差分进化算法;啤酒液位控制系统;参数自适应控制;邻域搜索;PID参数整定
在整条啤酒包装生产线中,啤酒罐装机扮演着至关重要的角色。灌装机内部的贮液缸液位控制则是一项核心技术。贮液缸液位的精准控制会减少灌装过程中的冒酒、灌不满、液位偏高或低、增氧量和瓶颈空气超出标准等现象发生的概率,从而降低企业包装成本,提高生产效率,因此,贮液缸控制液位的研究显得尤为重要。目前,啤酒生产中液位控制通常采用PID控制器进行反馈控制,PID控制器结构简单、鲁棒性和适应性强,但由于实际对象通常具有非线性、时变不确定性、强干扰等特性,利用常规PID控制器难以达到理想的控制效果。PID控制参数主要有比例、积分和微分系数,如何选取PID参数直接影响液位控制效果的好坏。随着经济社会的高质量发展,企业对灌装技术的要求也越来越高,引入进化算法是提高控制精度的一个有效途径。
工程实践中和科学研究中存在很多非线性、非凸、不可微分、多模态、高维等复杂的优化问题,传统数学分析方法如:梯度下降法(Gradient Descent, GD)、共轭方向法(Conjugate Direction Method,GDM)以及拉格朗日乘子法(Lagrange Multiplier Method,LMM)在解决这类问题时效果不佳。进化算法(EA)从自然界中生物进化的得到学习和启发,不需要借助待优化问题的数学特征,并且使用方便、易于理解,鲁棒性较强,已经成为工程技术和研究人员解决优化问题的首选。近些年来,灰狼优化算[1]、布谷鸟算法[2]、萤火虫算[3]等进化算法相继被学者提出。
其中差分进化算法(Differential Evolution, DE)因其具有易于实现、供选择的变体多、收敛速度快、解精度高等优点得到了进化计算领域学者的关注,已经被成功应用到模式识别[4-5]、工业生产设计[6-7]、图像检测[8]、通信系统设计[9]等领域。差分进化算法是一种基于种群的启发式搜索算法,具有对最佳历史位置的记忆功能,可以应用于各种优化场景,包括约束、大规模、多目标、多模态和动态的优化。在IEEE Congress on Evolutionary Computation (CEC)2021单目标优化竞赛中,性能最好的前10名中有6名是在差分进化算法的基础上进行改进,由此可见差分进化算法现在仍然受到学者的青睐,因此,文中采用改进差分进化算法对贮液缸液位PID控制参数进行整定,进而提高灌装过程中液位控制的精确度和稳定性。
1 经典DE
为了寻找非线性、非凸、不可微分、多模态优化问题的全局最优解,Storn和Price于1995年提出差分进化算法[10]。差分进化算法是一种基于种群的启发式搜索算法,与其他算法类似,DE主要由4个步骤组成——初始化种群(Initialization)、变异操作(Mutation)、交叉操作(Crossover)以及选择操作(Selection),算法通过不断迭代变异、交叉和选择操作向全局最优解逼近。
1.1 初始化种群
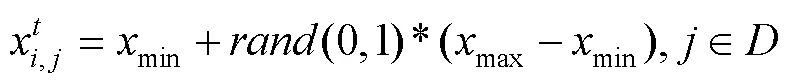

1.2 变异操作
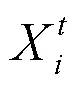
常用5种的变异策略如下
1)DE/rand/1:
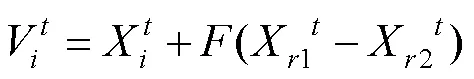
2)DE/best/1:
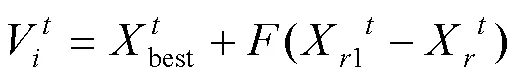
3)DE/current-to-best:
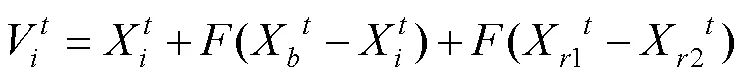
4)DE/best/2:
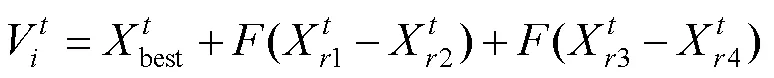
5)DE/rand/2:
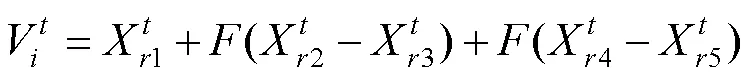
式中:是从种群中随机选择的个体,索引,并且与不同,代表种群中适应度值最好的个体,称为差分矢量,代表缩放因子,较小的F值有利于种群进行细粒化搜索。DE/rand/2变异策略在二维平面的简单展示见图1。
1.3 交叉操作
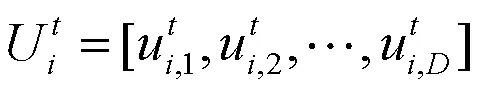
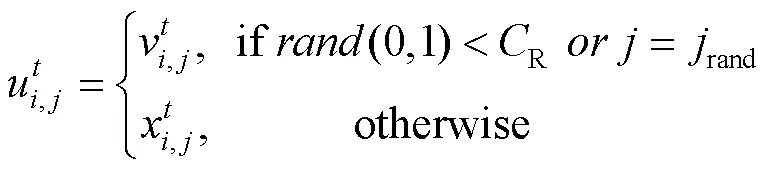
式中:R为交叉概率,通常在[0,1]之间取值;rand为[1,]之间的一个整数以确保试验向量不同于目标向量,较大的R值有利于算法的勘探能力,较小的R值有利于算法开发能力。
1.4 选择操作

2 相关工作

为了提高DE算法搜索效率,提出了一种新的变异策略,试图平衡全局搜索和局部搜索。引入个体之间分布信息判断个体收敛性来动态调节算法中的参数,并且对缩放因子和交叉概率采用自适应的策略。
3 改进的差分进化算法
3.1 建立新的变异策略
DE的性能在很大程度上依赖于变异,差分进化算法的搜索过程从基向量开始,然后将不同的向量作为干扰加入其中,沿着差分向量的方向进行搜索,逐渐向全局最优解收敛。在众多变异策略之中,DE/rand/1偏向于随机搜索具有很强的多样性,但没有加入种群中最佳解信息,导致后期收敛性能不足;DE/best/1引入了种群中最佳解信息,但可能会出现陷入局部最优的情况。受Zhang等[20]所提出的变异策略DE/current-to-pbest/1和Wang等[21]提出的基于邻域的粒子群算法(DNSPSO)的启发,文中提出一种新的变异策略,加入邻域的信息,见式(10)。
DE/current-to-pbest/1变异公式见式(9)。
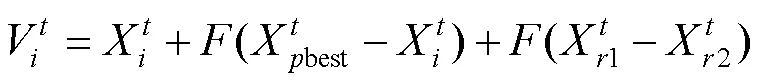
DE/best-to-neighbors/1:
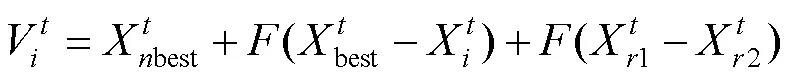
式中:为个体N个邻域中适应度值最好的个体;为整个种群中适应度值最好的个体,该变异策略结合了局部最优和全局最优解的信息,可以帮助算法跳出局部最优解,表现出较好的收敛性能。N为6时的邻域搜索示意图见图2。
3.2 动态调整邻域因子
其中邻域的大小对算法的开发和探索能力有很大的影响,的值较大使算法倾向于DE/best/1策略,的值较小使算法倾向于DE/rand/1策略,因此固定的值不适合于所有函数。由于种群是随机初始化生成,在算法执行的早期阶段种群较为分散,通过变异、选择等操作种群逐渐向全局最优收敛。我们引入个体之间的欧式距离,通过判断种群的分布情况,动态分配的选择邻域个数。在算法整个周期内对于适应度较差个体分配更多的邻居个数,适应度值好的个体则分配更少的邻域个数。

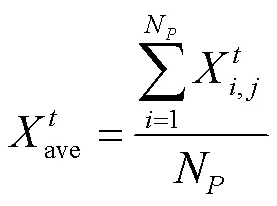

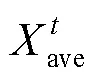
3.3 F和的CR自适应调整
控制参数和R的值对同样DE性能有着很大的影响,在2个参数交叉概率R和缩放因子之间,R对问题的性质如多模态更为敏感,而对收敛速度更为敏感。根据“天下没有免费的午餐”定理[22],一个算法在某组优化问题上的性能优于另一个算法,那么在其他优化问题上情况必然相反。如果采用一组固定的参数,算法可能只对某个优化问题有较好的性能,文中采用文献Jde[23]中所提出自适应改变控制参数的方法,为每一代中的每个个体生成控制参数。
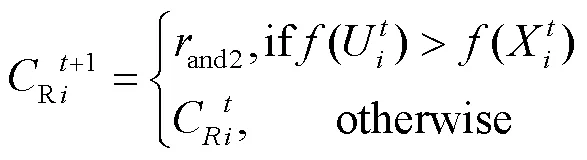
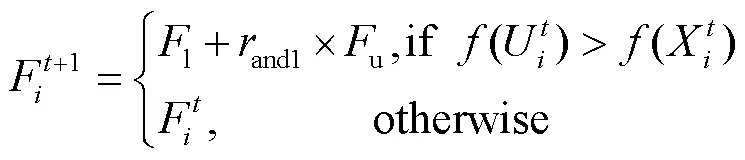

3.4 算法伪代码
与原始DE相比,文中主要从两方面改进:创建一种新的变异方式,融合了邻域和全局最优解的信息,能有效增强种群的多样性;对于邻域个数、缩放因子和交叉概率设置了自适应策略更新参数。
算法1:NSaDE伪代码如下:
1.Input:
p: population size
D: Problem dimension
maxMaximum number of function evaluations
2.Randomly initializepindividuals
3. Generate control parameterandRfor each individual
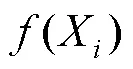
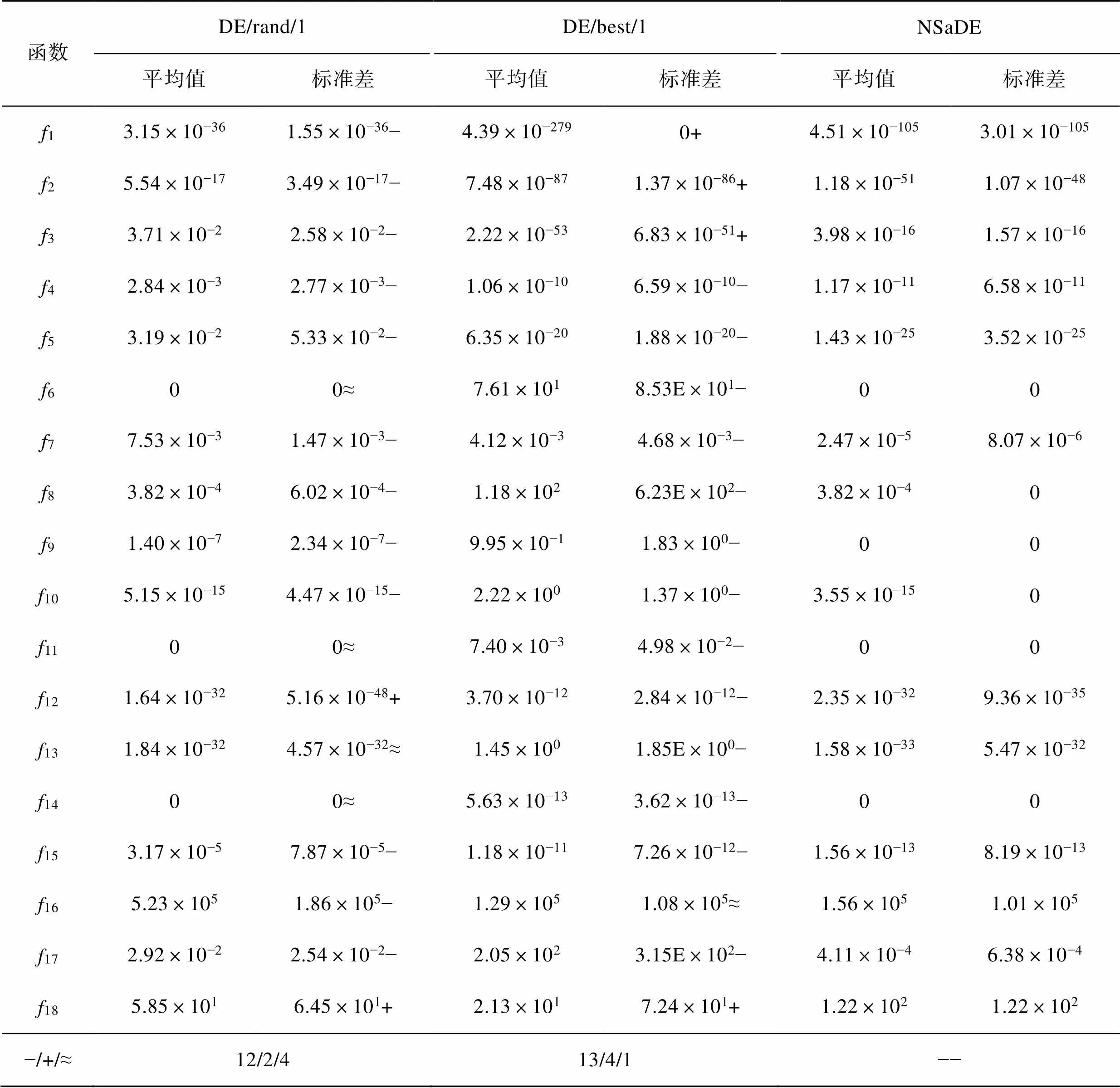
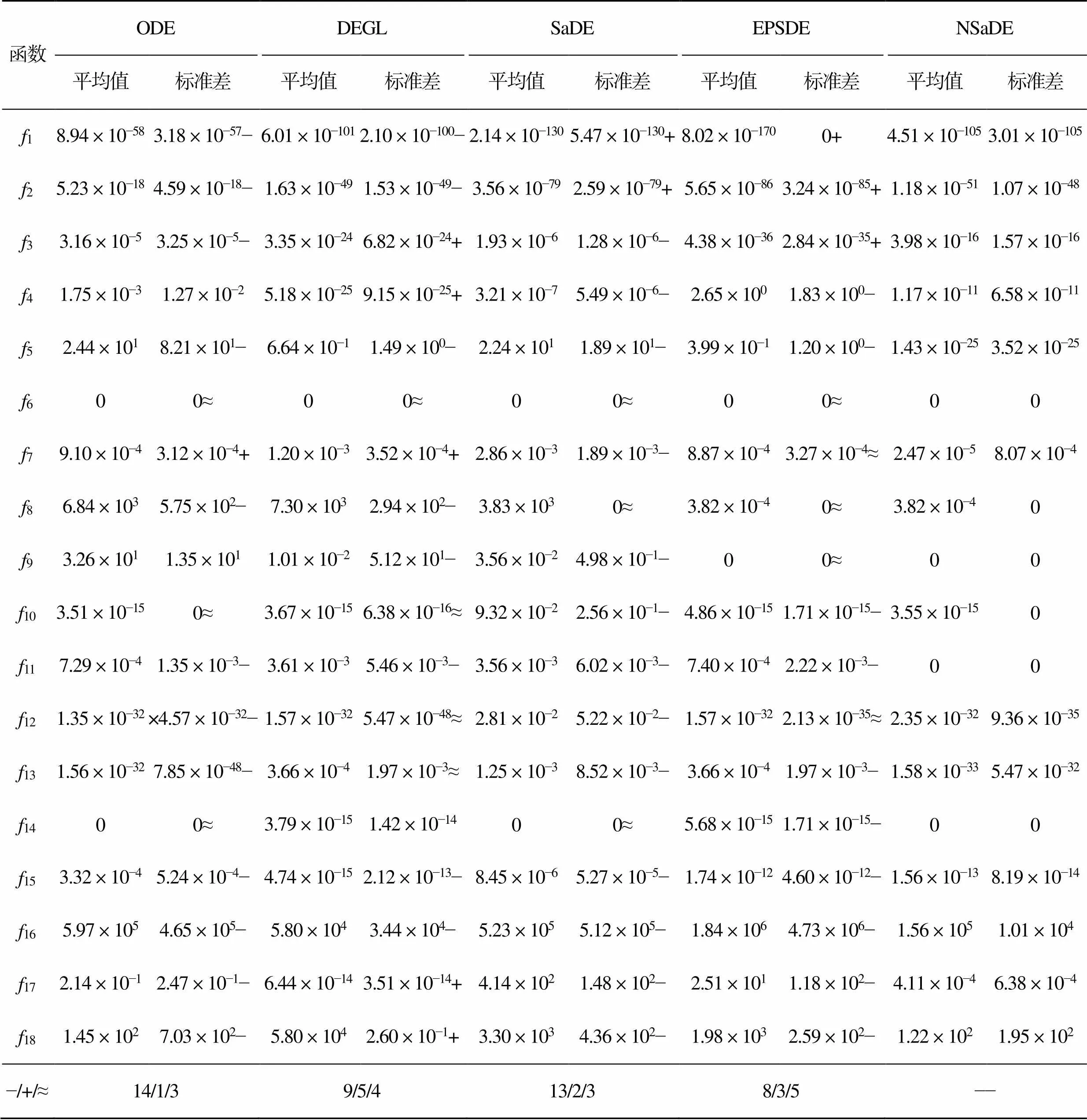
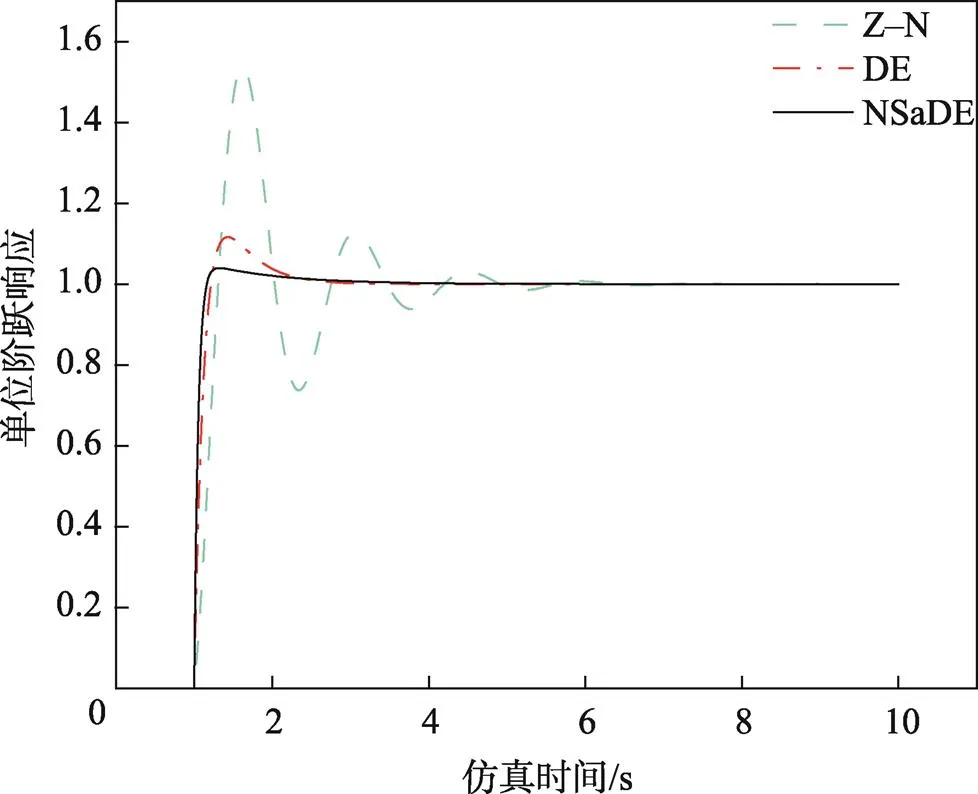
5. while FEs 7. for i = 1:pdo 12. FEs = FEs + 1 15. else 16. updateRandaccording to Eq.(14) and Eq.(15) 17. end if 18. end for 19. end while 仿真实验的运行环境为:AMD Ryzen 7 4800H CPU,主频2.90 GHz,内存16 GB, Windows 10,64位操作系统,实验仿真软件采用Matlab R2021a。 文中采用的18个测试函数来验证所提出算法的有效性,其中17为单峰测试函数,可以检验算法收敛速度和精度;813为多模态函数,具有多个局部最优解,可以检测算法跳出局部最优的能力;1418为CEC2005单目标优化竞赛中提出的测试函数,这些函数为带移位的组合函数,其地形较为复杂具有一定的欺骗性,因此有很大的难度。测试函数的函数名、搜索范围以及全局最优值见表1。 表1 18个测试函数 Tab.1 18 test functions 表2 NSaDE与基本DE对比实验结果 Tab.2 Experimental results of comparison between NSADE and basic DE algorithm 从表2中可以看出,与DE/rand/1相比,NSaDE在18个测试函数上有12个取得了更好的结果,4个测试函数上性能接近,仅有2个结果比NSaDE更优。与DE/best/1相比,NSaDE在13个测试函数上取得了更好的结果,而 DE/best/1在仅4个测试函数上表现的比NSaDE更优,1、2和3是单峰问题,18是移位单峰函数,原因是DE/best/1作为一种贪婪策略对这些简单的单峰和多峰问题具有更好的勘探能力,但是在处理具有多个局部最优问题时,可能使算法陷入停滞状态。在表3中与4种改进算法对比结果看出,对于绝大多数测试函数NSaDE取得的结果具有明显的优势。综上所述,文中所提出NSADE算法有较强的全局搜索能力和较好的稳定性。 为了验证文中提出的改进差分进化算法在啤酒液位灌装机贮液缸控制系统上的有效性和可靠性,在Matlab/Simulink中进行仿真实验。传统的PID控制原理见图3,采用比例、积分、微分调节,其中比例系数(p)、积分系数(i)、和微分系数(d)对系统的性能有很大的影响,只有3个参数合理配置时,系统才能处于最佳的状态。 表3 NSaDE与4种改进算法对比实验结果 Tab.3 Experimental results of comparison between NSADE and 4 improved algorithm 采用传统的Ziegler–Nichols(Z–N)法、基本DE算法和文中改进的NSaDE算法优化的PID控制对啤酒灌装机贮液缸液位进行仿真对比试验。实验中,选择绝对误差积分(ITAE)准则作为改进差分进化算法的适应度函数,见式(18),其值越小越好。通过实数编码将p、i、d3个参数作为一个个体,以ITAE作为算法评估函数,通过不断迭代搜索一组最佳的PID控制参数。 图4 基于改进差分进化算法的PID优化结构 仿真参数设置:以单位阶跃信号作为系统输入,p、i、d上下界设置为[0.001,100],仿真时间为10 s,采样频率为100 Hz;基本DE算法种群规模P=50,和R分别设置为0.7和0.9;NSaDE种群规模P=50,最大迭代次数(max)为1 500次。 从表4的结果来看,经NSaDE法整定的系统超调量较小,响应速度更快,调节时间相比于Z–N和DE法分别缩短了59.71%和10.04%,上升时间相比于Z–N和DE法缩短了12.5和3.44%。从图5中可以看出,NSaDE方法可以获得更好的整定结果。传统的Z–N法获得的系统响应曲线振荡次数较多并且始终存在稳态误差,而DE和NSaDE实现了零误差,具有更高的控制精度。综上所述,采用NSaDE方法整定的PID参数对啤酒灌装机贮液缸液位能进行稳定的控制,在目标值追踪效果上好于Z–N法和基本DE方法,其控制器性能能够实现啤酒灌装机的生产要求。 表4 3种方法主要性能指标对比 Tab.4 Comparison of main performance indexes of 3 methods 图5 Z–N法、DE法和NSaDE法整定后的单位响应曲线 为了克服差分进化算法搜索性能、容易陷入局部最优解的不足,文中提出了一种基于邻域的自适应差分进化算法——NSaDE算法。算法设计了一种新的变异方式,引入种群信息对邻域的个数进行自适应更新来提升算法局部和全局搜索的性能。在18个测试函数上进行仿真,与DE/rand/1、DE/best/1、SaDE、EPSDE、DEGL、ODE算法进行对比,在收敛速度、寻优精度都取得了较好的结果。将改进算法用于解决啤酒灌装机PID参数的优化问题,取代了烦琐的反复实验,节约了时间成本。仿真结果表明使用改进算法得到PID参数的系统有着更小的超调量、更快的响应速度,能够实现对液位的精准控制,保证啤酒罐装过程中实现稳定运行和啤酒生产的质量和产量。 [1] SEYEDALI M, SEYED MOHAMMAD, ANDREW LEWSIA. Grey Wolf Optimizer[J]. Advances in Engineering Software, 2014: 46-61. [2] GANDOMI A H, YANG Xin-she, ALAVI A H. Erratum To: Cuckoo Search Algorithm: A Metaheuristic Approach to Solve Structural Optimization Problems[J]. Engineering With Computers, 2013, 29(2): 245. [3] YANG Xin she. Firefly Algorithm, Stochastic Test Functions and Design Optimization[J]. International Journal of Bio-Inspired Computation, 2010, 2(2): 78-84. [4] WANG Li-zhou, HONG Guang-hao. A Singular Critical Point for some Variational Free Boundary Problem in Five Dimensions[J]. Journal of Mathematical Analysis and Applications, 2015, 426(2): 855-863. [5] 何庆飞, 陈小虎, 姚春江, 等. 基于最小二乘支持向量分类机的齿轮泵故障诊断研究[J]. 流体机械, 2019(8): 32-36. HE Qing-fei, CHEN Xiao-hu, YAO Chun-jiang, et al. Gear Pump Fault Diagnosis Research Based on Least Squares Support Vector Classification Machine[J]. Fluid Machinery, 2019(8): 32-36. [6] SEGUNDO E, AMOROSO A L, MARIANI V C, et al. Economic Optimization Design for Shell-and-Tube Heat Exchangers by a Tsallis Differential Evolution[J]. Applied Thermal Engineering, 2017, 111: 143-151. [7] AYALA H, VICENTE H, MORAIS, et al. Design of Heat Exchangers Using a Novel Multi-Objective Free Search Differential Evolution Paradigm[J]. Applied THERMAL ENGINEERING: Design, Processes, Equipment, Economics, 2016, 94: 170-177. [8] ZHOU Zhi-li, YANG C N, CHEN Bei-jing, et al. Effective and Efficient Image Copy Detection with Resistance to Arbitrary Rotation[J]. IEICE Transactions on Information and Systems, 2016, 99(6): 1531-1540. [9] ZHANG, WU Z. Spectrum Allocation by Wave Based Adaptive Differential Evolution Algorithm[J]. Ad hoc networks, 2019, 94: 1-8. [10] STORN R, PRICE K. Differential Evolution-A Simple and Efficient Heuristic for global Optimization over Continuous Spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. [11] 荆涛, 田锡天. 基于蒙特卡洛-自适应差分进化算法的飞机容差分配多目标优化方法[J]. 航空学报, 2022, 35(3): 569-580. JING Tao, TIAN Xi-tian. Multi-Objective Optimization Method for Aircraft Tolerance Allocation Based on Monte Carlo-Adaptive Differential Evolution Algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2022, 35(3): 569-580. [12] 李钊, 袁文浩, 任崇广. 基于搜索空间划分与Canopy K-means聚类的种群初始化方法[J]. 控制与决策, 2020, 35(11): 2767-2772. LI Zhao, YUAN Wen-hao, REN Chong-guang. Population Initialization Based on Search Space Partition and Canopy Kmeans Clustering[J]. Control and Decision, 2020, 35(11): 2767-2772. [13] ZHANG Jing-hua, HAN Pu. Multi-Algorithm and Multi-Population Co-Optimization Differential Evolution Algorithm[J]. Journal of System Simulation, 2018, 30(5): 1690-1699. [14] SUN Can, ZHOU Xin-yu, Wang Ming-wen. A Multi-Strategy Differential Evolution Algorithm Combined with Neighborhood Search[J]. Journal of System Simulation, 2020, 32(6): 1071-1084. [15] YI Wen-chao, GAO Liang, LI Xin-yu, et al. A New Differential Evolution Algorithm with a Hybrid Mutation Operator and Self-Adapting Control Parameters for Global Optimization Problems[J]. Applied Intelligence, 2015, 42(4): 642-660. [16] 徐英杰, 阎晓琳, 邓武. 基于小波基函数的差分进化算法缩放因子改进方法及应用[J]. 云南民族大学学报(自然科学版), 2020, 119(1): 33-38. XU Ying-jie, YAN Xiao-lin, DENG Wu. Scaling Factor Improvement Method of Differential Evolution Based on Wavelet Basis Function and Its Application[J]. Journal of Yunnan Minzu University (Natural Sciences Edition), 2020, 119(1): 33-38. [17] STANOVOV V, AKHMEDOVA S, SEMEKIN E. NL-SHADE-RSP Algorithm with Adaptive Archive and Selective Pressure for CEC 2021 Numerical Optimization[C]// 2021 IEEE Congress on Evolutionary Computation (CEC), IEEE, Kraków Poland, 2021: 17-24. [18] TANABE R, FUKUNAGA A. Success-History Based Parameter Adaptation for Differential Evolution[C]// 2013 IEEE Congress on Evolutionary Computation, 2013: 71-78. [19] 杨紫晴, 姚加林, 伍国华, 等. 集成协方差矩阵自适应进化策略与差分进化的优化算法[J]. 控制理论与应用, 2021, 36(10): 1493-1502. YANG Zi-qing, YAO Jia-lin, WU Guo-hua, et al. Ensemble Optimization Algorithm from Covariance Matrix Adaptive Evolution Strategy and Differential Evolution[J]. Control Theory & Applications, 2021, 36(10): 1493-1502. [20] ZHANG Jing-qiao, SANDERSON A C. JADE: Adaptive Differential Evolution with Optional External Archive[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958. [21] WANG Hui, SUN Hui, LI Chang-he, et al. Diversity Enhanced Particle Swarm Optimization with Neighborhood Search[J]. Information Sciences, 2013, 223: 119-135. [22] DAVID H WOLPERT, WILLIAM G. MACREADY No Free Lunch Theorems for Optimization[J]. IEEE Transactions on Evolutionary Computation (S1089-778X), 1997, 1(1): 67-82. [23] BREST J, GREINER S, BOSKOVIC B, et al. Self- Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems[J]. IEEE Trans Evolutionary Computation, 2006, 10(6): 646-657. [24] QIN A K, HUANG V L, SUGANTHAN P N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417. [25] MALLIPEDDI R, SUGANTHAN P, PAN Q, et al. Differential Evolution Algorithm with Ensemble of Parameters and Mutation Strategies[J]. Applied Soft Computing Journal, 2010, 11(2): 1679-1696. [26] DAS S, ABRAHAM A. Differential Evolution Using a Neighborhood-Based Mutation Operator[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(3): 526-553. [27] RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition-Based Differential Evolution[J]. IEEE Transactions on Evolutionary Computation, 2014, 12(1): 64-79. [28] DERRAC J, GARCÍA S, MOLINA D, et al. A Practical Tutorial on the Use of Nonparametric Statistical Tests as a Methodology for Comparing Evolutionary and Swarm Intelligence Algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(1): 3-18. [29] 黄卓超, 张伟, 王亚刚. 改进粒子群算法的啤酒灌装机液位控制PID参数整定[J]. 包装工程, 2020, 41(19): 159-165. HUANG Zhuo-chao, ZHANG Wei, WANG Ya-gang. PID Parameter Setting of Liquid Level Control for Beer Filling Machine Based on Improved Particle Swarm Algorithm[J]. Packaging Engineering, 2020, 41(19): 159-165. PID Parameter Setting of Liquid Level Control for Beer Filling Machine Based on Improved Differential Evolution Algorithm WANG Chao-fenga, SI Cheng-yonga,b, SHEN Jian-qiangb (a. School of Optical-Electrical and Computer Engineering b. Sino-German College, University of Shanghai for Science and Technology, Shanghai 200093, China) The work aims to propose an improved neighborhood based differential evolution algorithm and apply it to PID parameter optimization setting to solve the problems of difficulty, nonlinearity and hysteresis in beer liquid level control system, thus improving the work efficiency of filling machine and the beer quality. The differential evolution algorithm was improved to design a new mutation strategy and introduce the neighborhood search operation in the mutation link. According to the current population distribution, real-time adaptive allocation of the number of neighborhoods was carried out to enhance the global and local search ability of the algorithm. The proposed algorithm was compared with 2 basic differential evolution algorithms and 4 improved differential evolution algorithms and its performance was verified by 18 test functions. From the simulation results, compared with the basic differential evolution algorithm, the PID parameter setting by the improved differential evolution algorithm could reduce the adjustment time by 0.22 s, the rise time by 0.04 s, and the overshoot by 7.63%. Through the improved differential evolution algorithm, the PID parameter setting of the beer filling machine’s liquid level is optimized, which significantly improves the overshoot, rise time and steady-state error of the control system and realizes the stable control of the liquid level. differential evolution algorithm; beer level control system; parameter adaptive control; neighborhood search; PID parameter setting TP273+.2 A 1001-3563(2022)19-0310-10 10.19554/j.cnki.1001-3563.2022.19.038 2020–10–13 上海市青年科技英才扬帆计划(18YF1417400) 王超锋(1997—),男,硕士生,主攻智能优化算法。 司呈勇(1986 —),男,博士,副教授,主要研究方向为进化计算、约束优化、多目标优化算法等相关人工智能理论及应用。 责任编辑:曾钰婵
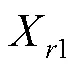
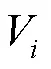

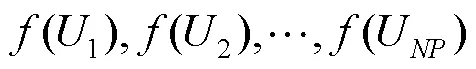
3.5 数值仿真


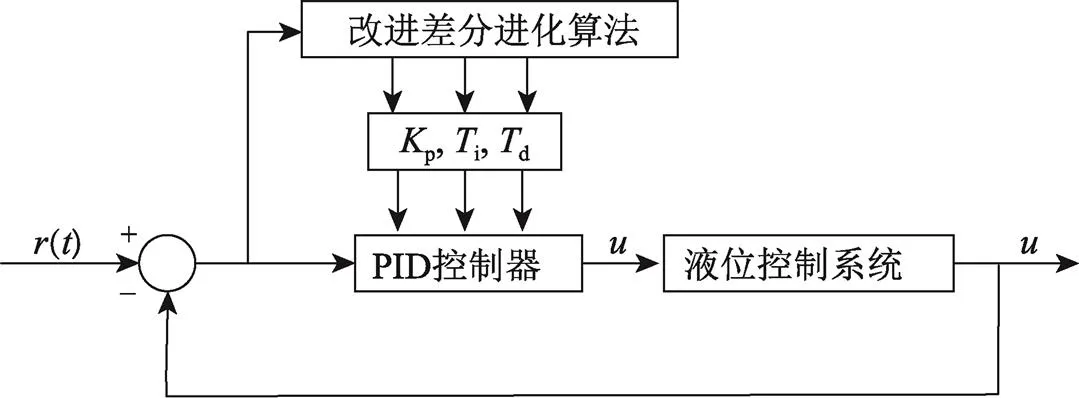
4 啤酒灌装机贮液缸液位PID优化控制
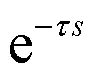
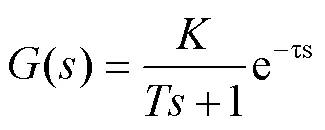

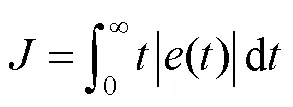

5 结语
