一种新型六自由度SCARA机器人设计与运动学分析

张良安，王祥，谢胜龙

一种新型六自由度SCARA机器人设计与运动学分析

张良安1，王祥1，谢胜龙2

（1.安徽工业大学 机械工程学院，安徽 马鞍山 243000；2.中国计量大学 机电工程学院，杭州 310018）

针对传统四自由度SCARA机器人末端灵活性不足的问题，设计一种新型的六自由度SCARA机器人。首先在传统四自由度SCARA机器人结构特点分析的基础上，通过改进其末端结构以增加机器人的自由度，从而提高其末端的灵活性。然后分别采用D–H参数法与代数法建立该机器人的运动学正解模型与逆解模型。在此基础上，采用对比法在Matlab的Robotics Toolbox工具箱中对该机器人开展仿真分析，验证机器人运动学模型的正确性。最后，基于五次多项式插值算法对机器人开展轨迹规划研究。实验结果显示该机器人的运动轨迹、速度与加速度曲线光滑连续，没有任何断点与突变点。表明该机器人运动平稳，具有良好的运动学性能，从而为后续该机器人的运动控制奠定了良好的基础。

SCARA机器人；D–H参数法；机器人运动学；五次多项式插值；轨迹规划

机器人技术已经在3C行业、食品包装、汽车制造、喷砂打磨以及金属加工等行业中广泛运用[1]。采用工业机器人代替人工进行繁重的工作，不仅可以提高生产效率，节省人力资源，还可以满足可靠性的要求，进而保证了质量。SCARA（Selective Compliance Assembly Robot Arm）机器人不仅有较好的灵活性和很高的刚性[2]，还具有速度快、定位精度高、柔性好等特点，适用于自动化装配、码垛搬运等，适合工厂自动化生产，因此市场对其需求量越来越大[3]。

为了进一步提高生产效率，学术界对SCARA机器人开展了大量的研究，希望能提升其性能。王鹏等[4]为了避免在SCARA机器人工作过程中出现的运动耦合现象，改进了传统SCARA机器人的腕部结构，并且降低了运动控制的难度。林恒等[5]将SCARA的关键部件高度集成，简化整体机构，使整体重心降低，进而改善小臂受力状况。汤智先等[6]对SCARA机械臂的结构进行分析，通过改变底座几何结构减小振动的产生。裴永超等[7]设计了一种直驱式SCARA机器人，采用力矩电机直接驱动各个关节，使得结构更加紧凑。王海峰等[8]对SCARA机器人进行传动方案优化及机械结构设计。Bruzzone等[9]利用旋转关节驱动平行四边形机构的方式代替了移动关节，从而通过简单的平行四边形机构取代了丝杠轴与花键轴等零件的使用。杨梅等[10]为了完成焊接过程中的灵活操作，提出了一种新型SCARA机器人，该机器人通过增加摆动机构，扩大了SCARA的适用范围。曹峰等[11]提出了一种五自由度的SCARA机器人，在SCARA机器人基础上引入第四、第五双自由功能端，使得机器人具备了多样化功能，获得了更高的整体兼容性。Urrea等[12]将SCARA机器人增加了旋转和夹持的2个自由度夹爪以提高生产效率。刘凯等[13]提出一种新型工业机器人结构，增加了机器人的运动空间。

在一些复杂的工况环境中，上述研究都存在一定的弊端，如自由度不足、控制难度大、制造难度大、成本较高等。例如传统SCARA机器人只适用于平面定位和垂直方向的装配工作，在一些涂胶喷漆等高难度复杂工况的行业因其自由度的局限而受到约束，必须选择成本更高的六轴机器人。文中针对上述的问题与不足，解决传统SCARA机器人的不足和六自由度串联机器人的局限问题，在传统四自由度SCARA机器人结构的基础上，增加2个自由度以提高机构的灵活性和工作空间，使机器人可以更好地完成一些复杂的任务，以满足多领域的使用需求。

1 六自由度SCARA机器人机构设计

目前常见的SCARA机器人主要为四自由度或者末端加装一些可运动的夹爪来提高其灵活性。文中提出一种简易的模块化结构增加机器人本体的2个自由度，进而提高机器人的灵活性。

1.1 机器人方案概述

在对传统四自由度SCARA机器人的结构进行总结分析的基础上，为了达到增加机器人的灵巧性与结构紧凑的目的，确定新型六自由度SCARA机器人的设计原则如下。

1）在第1关节处，底座选用中空结构，伺服电机通过电机连接板与谐波减速器进行连接，然后减速器与安装法兰连接，最后安装法兰固定于底座上，实现电机安装在底座内部。这种结构有利于底座的平衡，使得大臂结构更加简洁，并在底座与大臂上安装限位装置，进行机械限位。

2）第2关节处，伺服电机安装在小臂上，其传动机构与第1关节处相似，虽然相对于电机安装在大臂上会增加转动惯量，但这种设计会使得整体结构变得简单，安装方便。从而提升了小臂的移动速度与灵敏度，降低了小臂对电机的驱动要求。

3）第3、4关节处，伺服电机同样安装在小臂上，通过同步带轮分别驱动丝杠轴与花键轴的运动，相较于将伺服电机安装在丝杠轴与花键轴机构末端，降低了机器人的重心。丝杠轴通过连接桥与花键轴连接，完成腕部的移动与转动。因花键轴末端增加了机构，为保证垂直方向的刚性，需加装2个丝杠导向轴。

4）第5关节处为腕部的摆动。此处相对于传统SCARA机器人，为增加灵活度而新增的机构。将伺服电机水平放置，其电机输出轴与花键轴垂直，通过安装座将电机固定于花键轴末端，通过同步带轮带动第6关节处电机安装板进行摆动，实现末端工具的上下摆动，使得SCARA机器人可以完成不仅限于平面的工作任务，其结构见图1。

5）第6关节的运动为末端工具的转动，与第4、5关节配合可以进行末端工具的姿态调整。电机安装在第5关节带动转动的电机安装板内，使得结构紧凑且安装与加工较为容易。而且运动与控制较为简单，有效确保运动平衡，降低负载，其结构见图2。

6）底座、大臂和小臂均采用Q235材料，使整个机器人的质量往底座方向后移，保证机器人的刚性与稳定性。五轴和六轴电机的安装座和安装板采用6061–T6材料进行加工，可以减轻末端质量和电机负载。

1.2 机器人虚拟样机设计

结合上述设计原则，基于SolidWorks软件对六自由度SCARA机器人进行三维建模，其总体结构见图3。所设计的六自由度SCARA机器人主要参数见表1。

图1 第5关节处机构

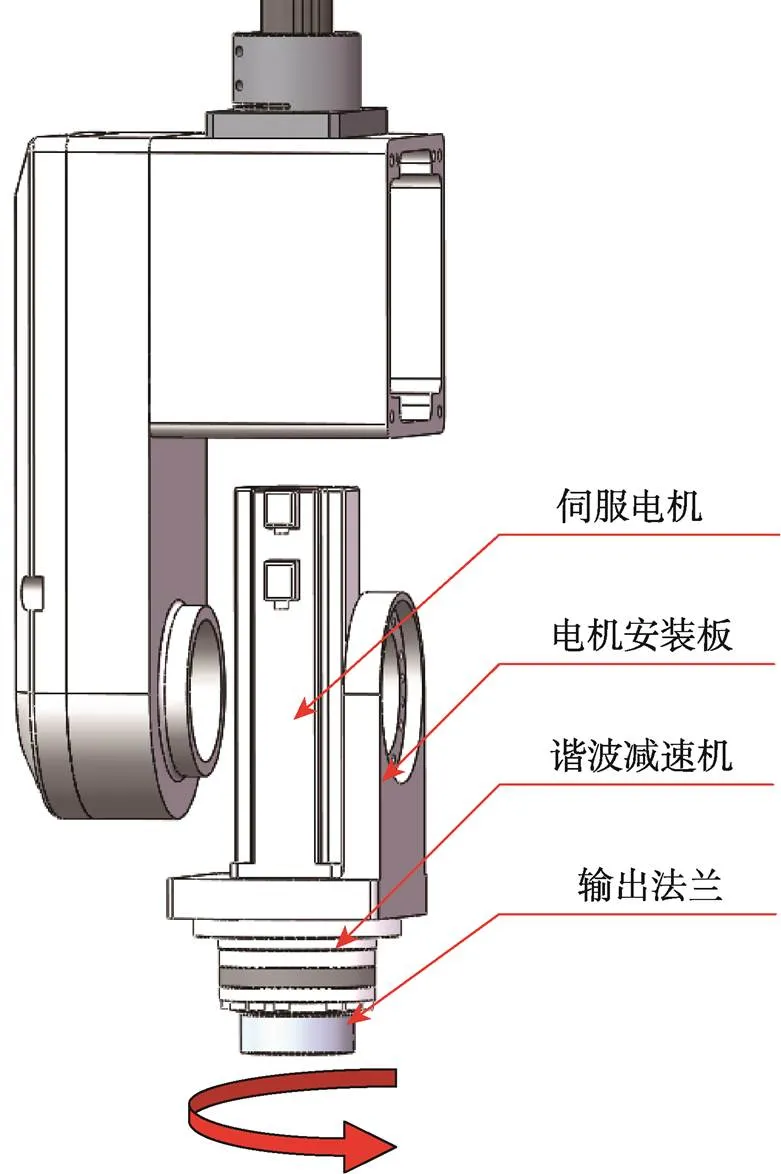
图2 第6关节处机构

该新型六自由度SCARA机器人工作空间的俯视图见图4。图4展示了该机器人的大臂转动与小臂转动所形成的工作空间的平面图。由于在该俯视图中新增的机构被遮挡无法展示，故在图5中展示新增机构的工作空间。

在图5中，当前三轴都固定不动时，传统四轴SCARA机器人末端只能实现相对于平面的旋转，即以4为圆心的灰色平面区域的圆。文中提出的六自由度SCARA机器人，在此基础上还有腕部的摆动，即图5中以5为圆心相交最大圆的椭圆区域（4与5重合），其运动范围为两处6所构成的弧段。此外，图5中2个最小椭圆代表第6关节即末端的转动，其转动角度范围为最小椭圆其内部区域。

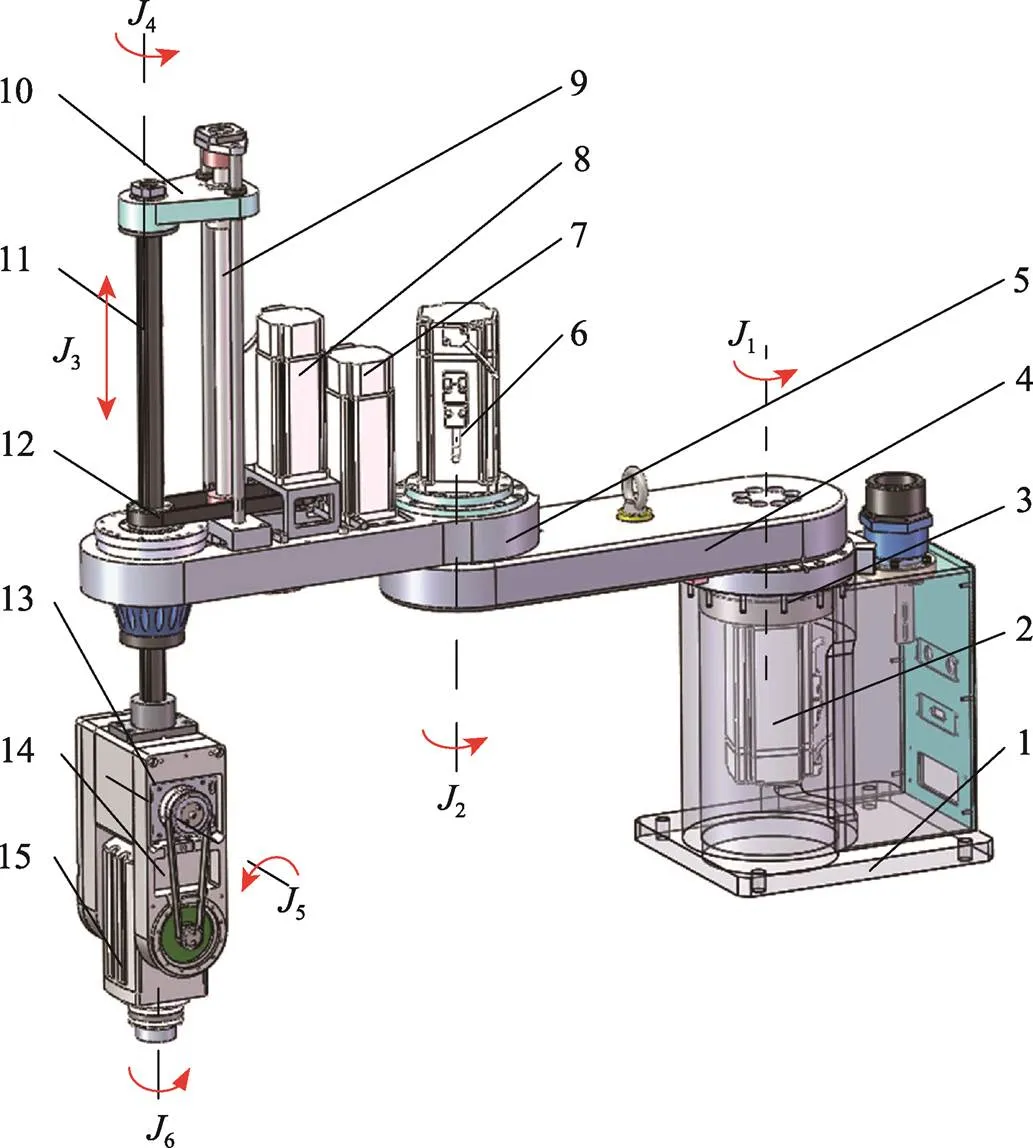
1.机箱底座；2.伺服电机；3.谐波减速器；4.大臂；5.小臂；6.伺服电机；7.伺服电机；8.伺服电机；9.丝杠主轴；10.连接桥；11.花键；12.同步带轮；13.伺服电机；14.同步带轮；15.伺服电机。

表1 六自由度SCARA机器人主要参数

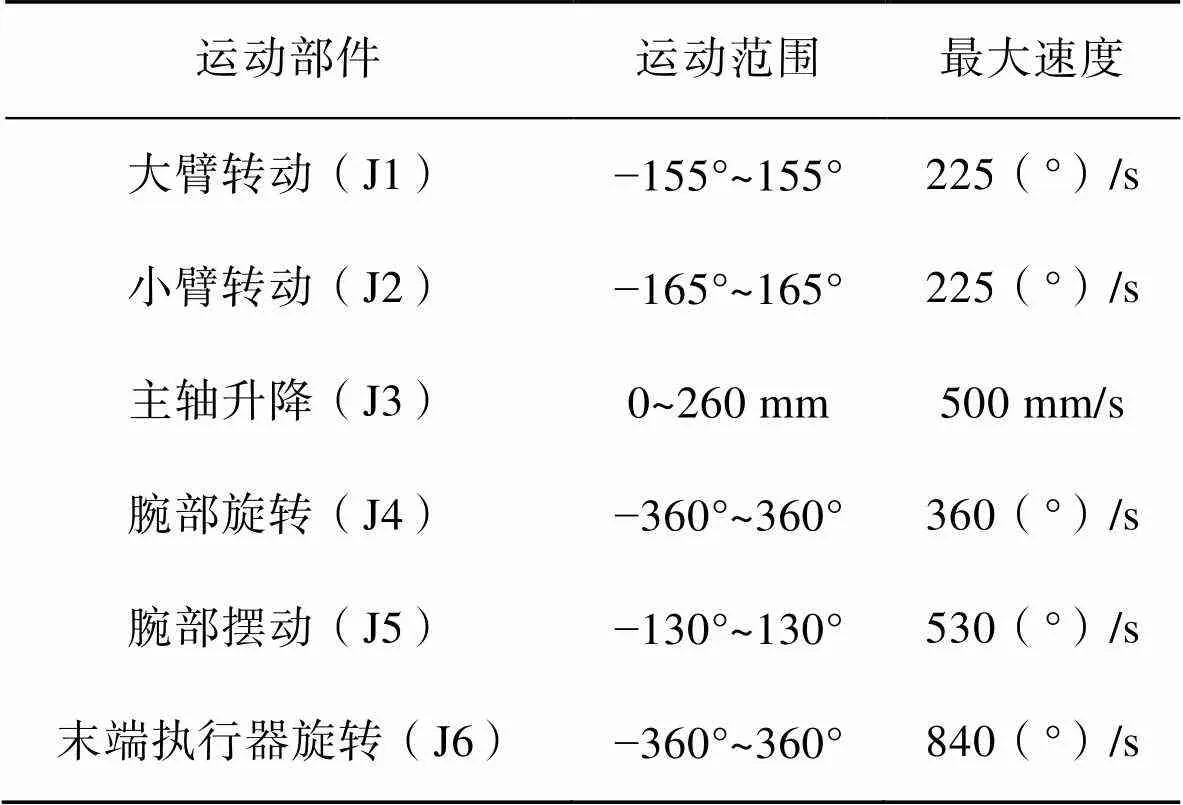
Tab.1 Main parameters of 6-DOF SCARA robot

由于该新型机器人在传统的四自由度SCARA机器人的末端增加了2个自由度，因此不仅增加了机器人的运动空间，末端还可以通过加装工具来提升机器人的灵巧性与适应性。此外，由于该新增的机构中大多数零件均采用标准件，只有少数固定安装板需要设计，因此具有制造简单、通用性强、成本低廉等优点。

2 六自由度SCARA机器人运动学研究

2.1 机器人正运动学模型

机器人的正运动学是为了解决机器人的末端位置求解问题[14]。建立如图6所示的D–H坐标[15]，机器人的机构运动简图见图7。

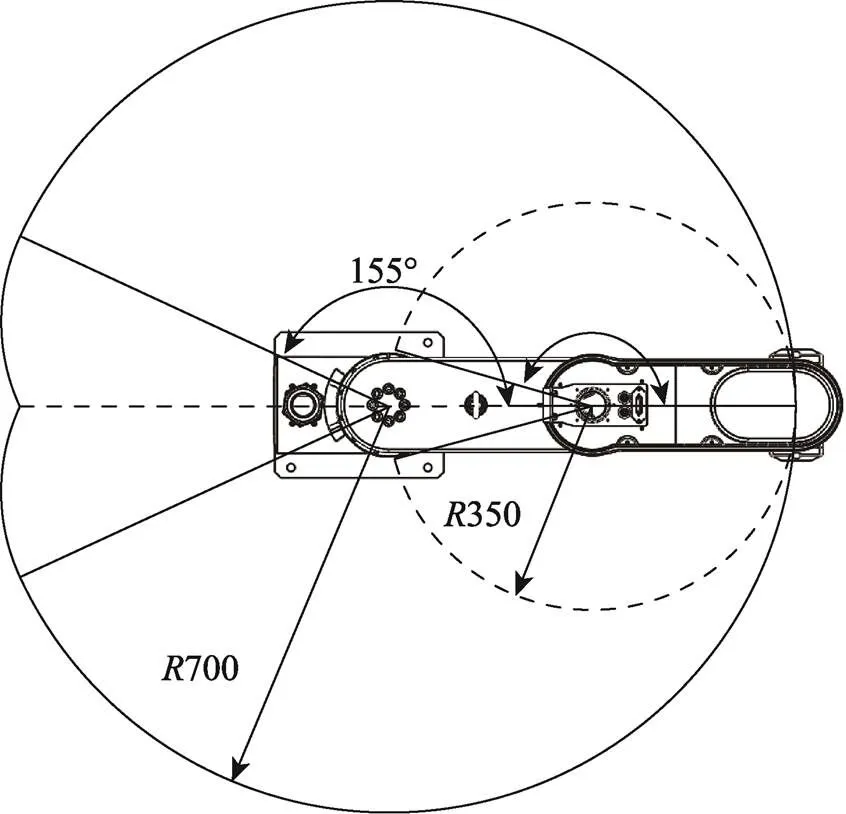
图4 六自由度SCARA机器人工作空间

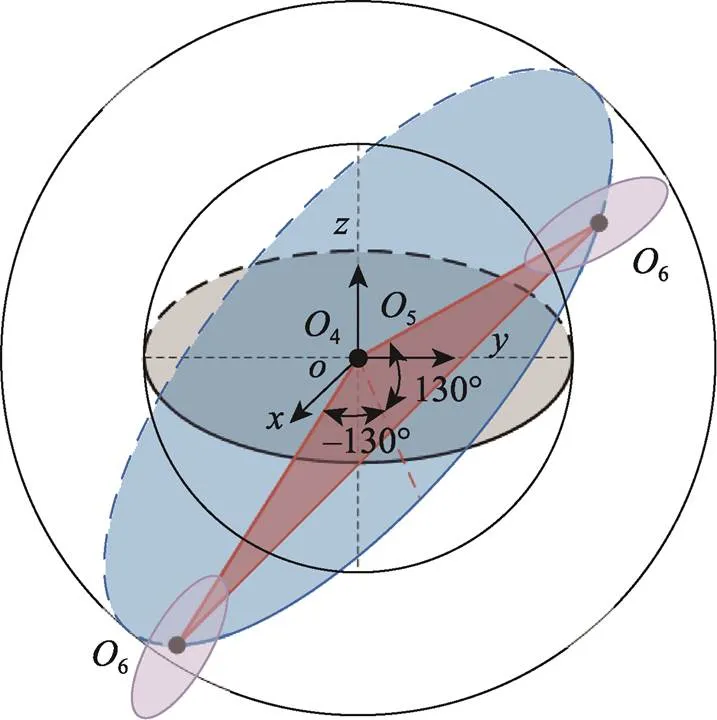
图5 六自由度SCARA机器人末端空间

列出该机器人的D–H参数见表2。

表2 D–H参数

Tab.2 DH parameters

已知关节轴的转角，通过运动学正解，即可求解末端姿态和位置，根据D–H坐标系与D–H参数表求得各连杆变换矩阵为：

(1)

式中：表示sin；表示cos。

运动学正解为：

(2)

式中：s表示sin；c表示cos。

提前计算年终奖个税，合理避税。各公司在发放年终奖时，建议合理安排好金额，适当注意避开个税税率中的几个“盲区”，计算税后收入，避免出现“企业多给，员工少拿”的尴尬。

图6 D–H坐标系建立示意图

Fig.6 Diagram for construction of coordinate system

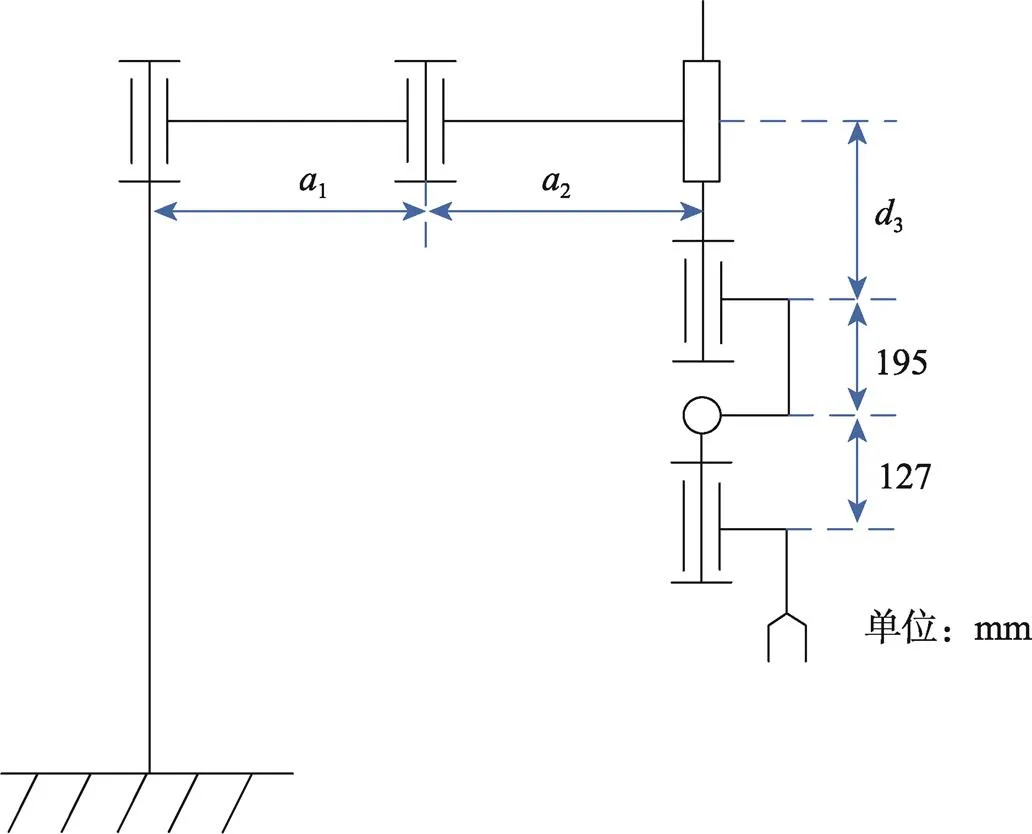
图7 机构运动简图

2.2 机器人逆运动学模型

利用代数法对六自由度SCARA机器人进行求解运动学逆解，可得到：

(3)

(4)

(5)

(6)

(7)

(8)

式中：表示sin；表示cos。

2.3 机器人运动学的验证

机器人运动学模型的验证包括正运动学模型的验证与逆运动学模型的验证，可以采用对比法进行比较验证。采用对比法对六自由度SCARA机器人正运动学模型的正确性进行验证时，给定各关节轴转动的角度值和移动的距离值分别为1=π/2、2=−π/3、3=0.15、4=π/3，5=π/6、6=−π/4，代入六自由度SCARA机器人末端执行器的位置和方程矩阵，再将同样的值代入Matlab的Robotic Toolbox中，并利用fkine函数进行求解。2次计算的结果一致，其结果为：

(9)

对比了2种方法计算出来的结果是一致的，因此可以验证其正运动学模型的正确。

采用对比法对六自由度SCARA机器人逆运动学模型的正确性进行验证时，将式（9）代入六自由度SCARA机器人逆运动学模型中，求解出其各个关节转动值和移动的距离值，然后将式（9）代入Matlab的Robotic Toolbox中，并利用ikine函数进行求解。2种方法解得的计算结果对比见表3。

表3 计算结果与仿真结果对比

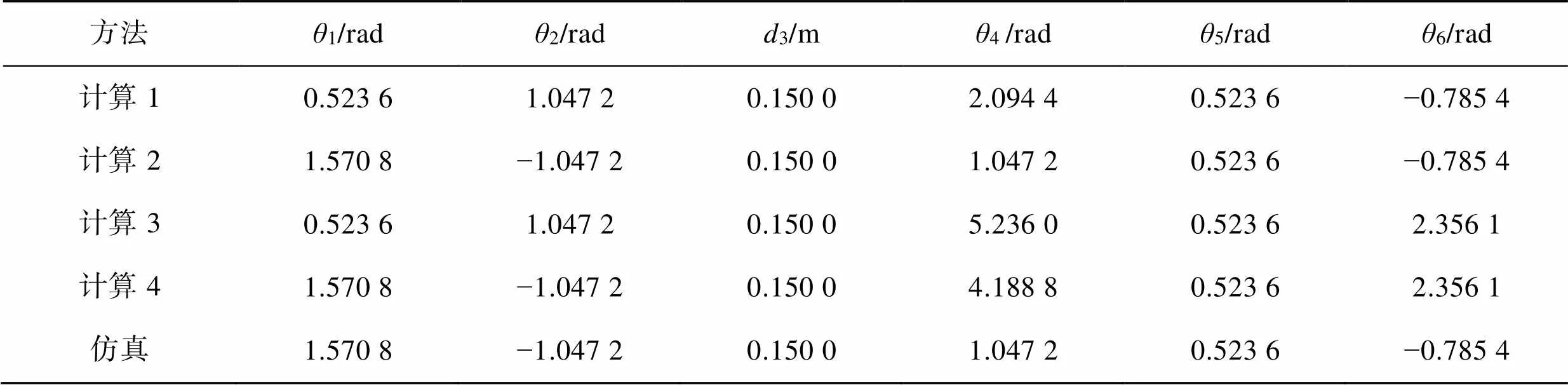
Tab.3 Results of calculation and simulation

在表3中，仿真结果一栏为利用ikine函数进行求解得到的结果，因逆运动学方程存在多解的问题，所以计算1—4分别对应上述逆运动学方程计算出来的结果。对比得出，在计算1—4的多组解中有1组解，即计算4的解与仿真所得的逆运动学解一致，证明了文中所计算的六自由度SCARA机器人的逆运动学方程的正确性。

3 机器人关节空间的轨迹规划

3.1 五次多项式插值算法的轨迹规划

在进行机器人的轨迹规划时，除了给定该段轨迹的开始点位置与速度，结束点位置与速度这4个约束条件外，若再给定该段轨迹开始点与结束点的加速度，则约束条件会从4个增加到6个。此时三次多项式将无法满足插值的精度需求，为了完成机器人这种复杂轨迹规划的插值任务，需要采用式（10）的五次多项式来进行轨迹规划。

(10)

式中：0、1、2、3、4、5为系数；为时间；为各关节的位移。

由边界约束条件解得系数为：

(11)

式中：0为起始位移；f为终止位移；为起始速度；为终止速度；为起始加速度；为终止加速度；f为终止时间。

3.2 实验仿真与分析

在机器人各个关节活动范围内，设定各关节运动的起始点与终止点的角度取值见表4，其中设定运动时间。

表4 关节角度的起始点与终止点

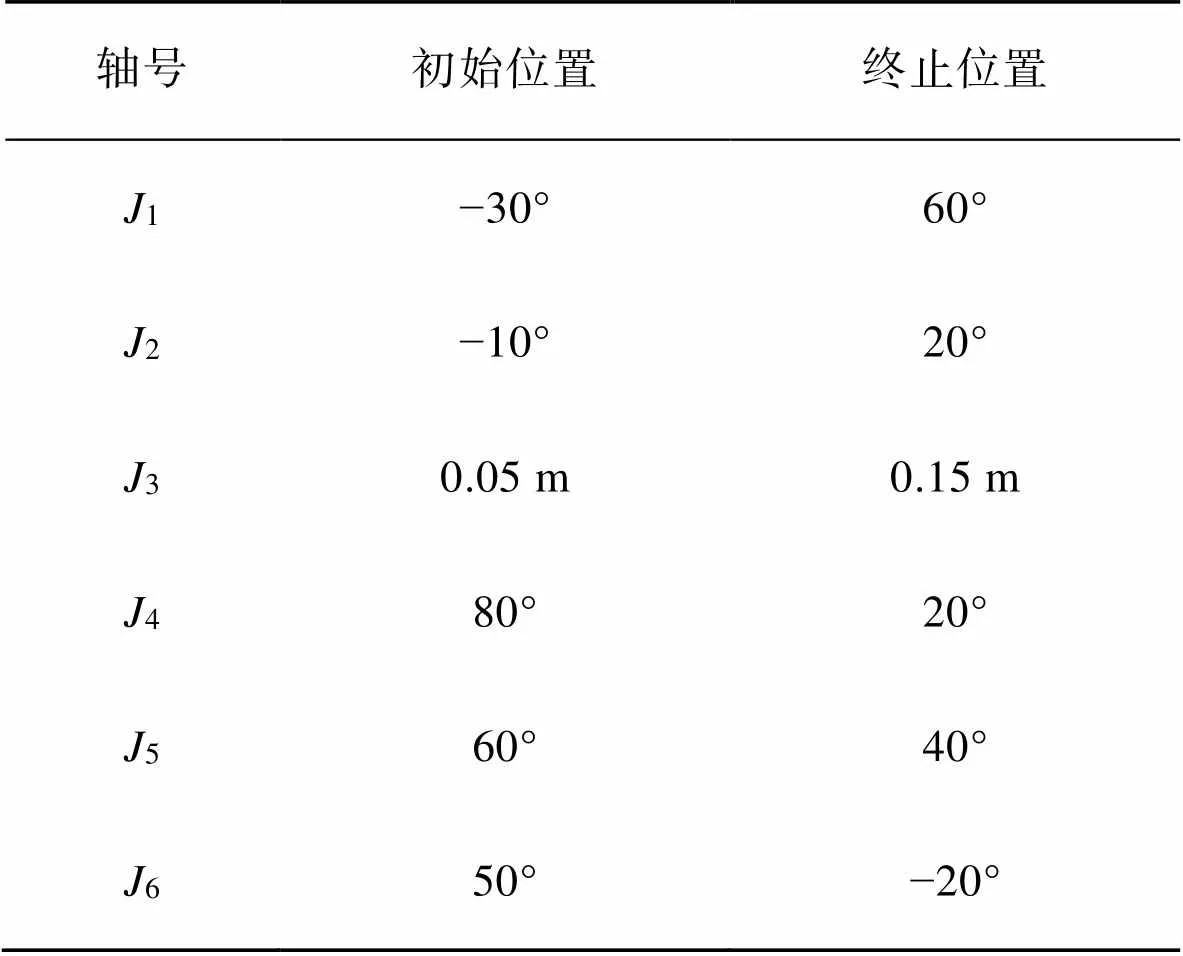
Tab.4 Starting and ending points of joint angles

计算得到各关节五次多项式插值算法的轨迹规划方程的系数见表5。

设定运动轨迹的起始与结束的速度均为0，在采用关节空间下的五次多项式进行轨迹规划时，各个关节运动的路径、速度以及加速度情况见图8。

图8的结果表明，所设计的六轴SCARA机器人各关节的位移、速度和加速度曲线都较为平滑且连续，未出现突变的情况，因此运动时电机不会出现抖动的情况，从而保证了该机器人运动的平稳性。

表5 五次多项式各系数

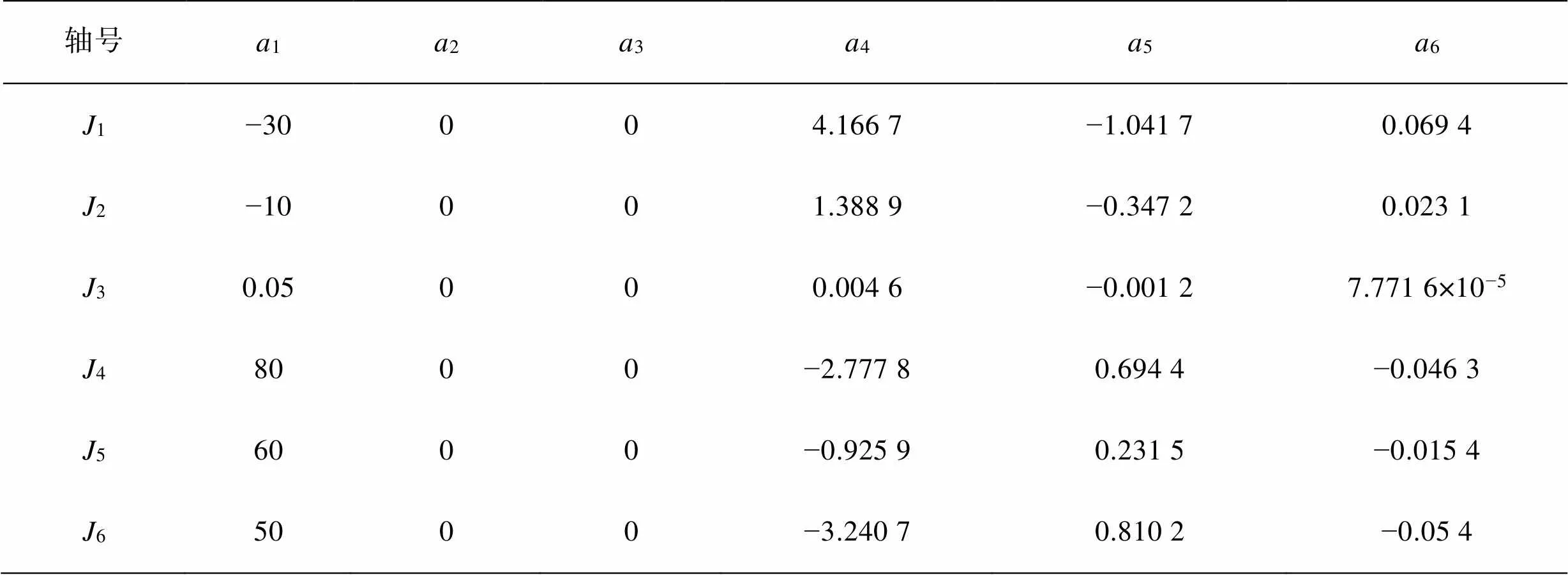
Tab.5 Coefficient of quintic polynomials

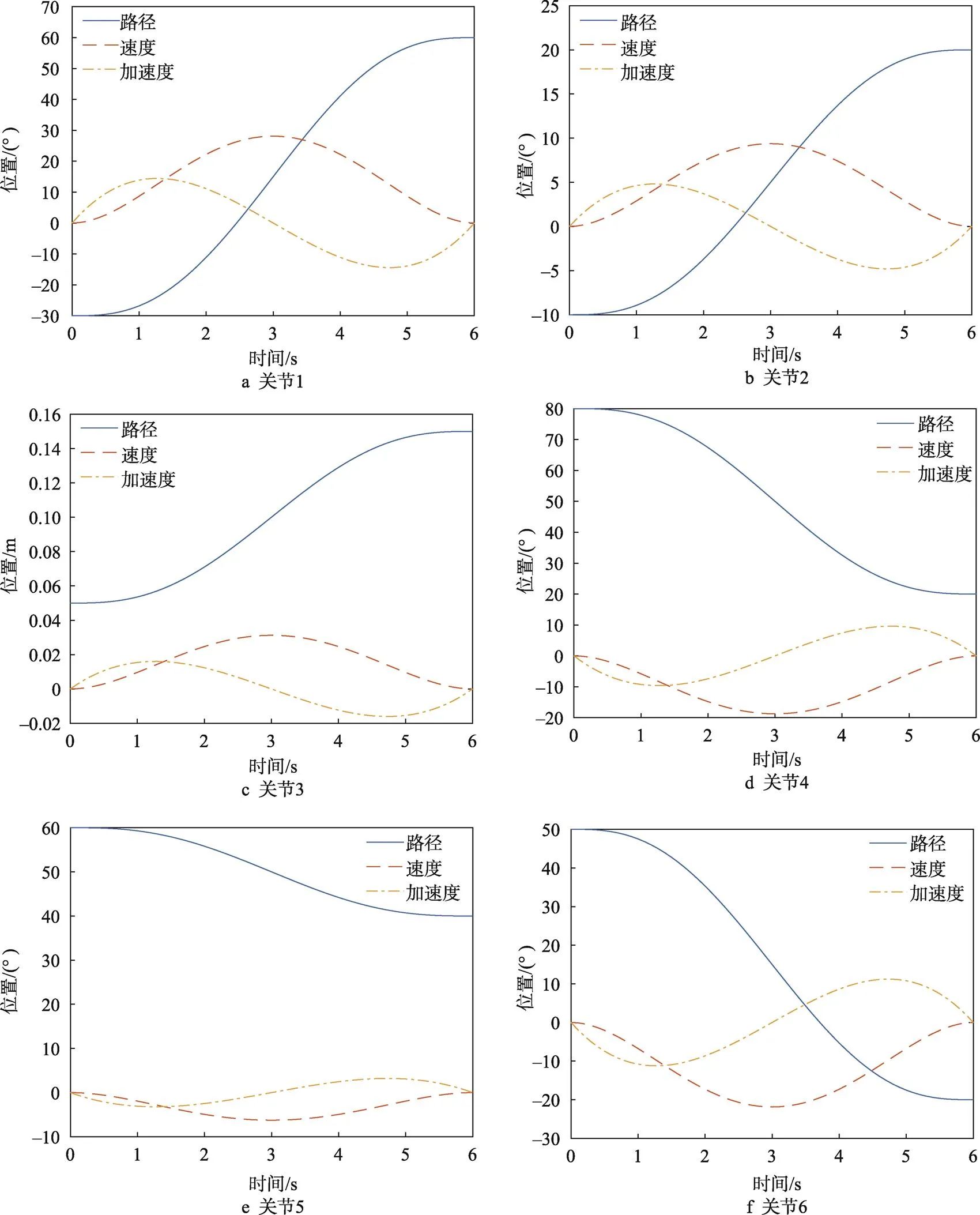
图8 五次插值各关节运动轨迹

4 结语

针对传统四自由度SCARA机器人末端灵活性不足的问题，改进其末端结构提高了机器人末端的灵活性。基于D–H参数法与代数法建立了该机器人的运动学模型并进行了仿真验证。通过开展轨迹规划研究，验证了机器人运动的平稳性，为样机的制造与控制奠定了良好的基础。

[1] 陈春春. 工业机器人产业: 现状、产业链及发展模式分析[J]. 互联网经济, 2019(1): 32-37.

CHEN Chun-chun. Robot Industry: Analysis of Present Situation, Industrial Chain and Development Model[J]. The Internet Economy, 2019(1): 32-37.

[2] 刘炀, 杨乐. SCARA机器人运动学和动力学仿真[J]. 现代机械, 2020(5): 15-19.

LIU Yang, YANG Le. Kinematic and Dynamic Simulation of SCARA Robot[J]. Modern Machinery, 2020(5): 15-19.

[3] 杨明, 张如昊, 张军, 等. SCARA四轴机器人控制系统综述[J]. 电气传动, 2020, 50(1): 14-23.

YANG Ming, ZHANG Ru-hao, ZHANG Jun, et al. Review of SCARA Four Axis Robot Control System[J]. Electric Drive, 2020, 50(1): 14-23.

[4] 王鹏, 张良安, 单家正. SCARA机器人结构改进与仿真分析[J]. 现代制造工程, 2015(12): 23-27.

WANG Peng, ZHANG Liang-an, SHAN Jia-zheng. Mechanical Structure Improvement and Simulation Analysis of SCARA Robot[J]. Modern Manufacturing Engineering, 2015(12): 23-27.

[5] 林恒, 谈士力, 陈凯, 等. 基于模块化的SCARA机器人结构设计与优化[J]. 工业控制计算机, 2015, 28(3): 47-48.

LIN Heng, TAN Shi-li, CHEN Kai, et al. Structure Design and Optimization of SCARA Robot Based on Modularization[J]. Industrial Control Computer, 2015, 28(3): 47-48.

[6] 汤智先, 潘颖. SCARA机械臂的仿真振动分析及振动测试[J]. 制造业自动化, 2020, 42(6): 21-26.

TANG Zhi-xian, PAN Ying. Simulation Vibration Analysis and Vibration Test of SCARA Manipulator[J]. Manufacturing Automation, 2020, 42(6): 21-26.

[7] 裴永超, 刘吉柱, 杨智涵, 等. 直驱式SCARA的结构设计和优化[J]. 煤矿机械, 2017, 38(10): 113-115.

PEI Yong-chao, LIU Ji-zhu, YANG Zhi-han, et al. Structure Design and Optimization of Direct Drive SCARA[J]. Coal Mine Machinery, 2017, 38(10): 113-115.

[8] 王海峰, 尹彬, 罗锐捷, 等. 四自由度SCARA机器人系统机构设计及运动学分析[J]. 机电工程, 2019, 36(12): 1320-1324.

WANG Hai-feng, YIN Bin, LUO Rui-jie, et al. Mechanism Design and Kinematics Analysis of 4-Dof SCARA Robot System[J]. Journal of Mechanical & Electrical Engineering, 2019, 36(12): 1320-1324.

[9] BRUZZONE L, BOZZINI G. A Statically Balanced SCARA-Like Industrial Manipulator with High Energetic Efficiency[J]. Meccanica, 2011, 46(4): 771-784.

[10] 杨梅, 赵冠群. 一种新型SCARA焊接机器人: 中国, 205798767U[P]. 2016-12-14.

YANG Mei, ZHAO Guan-qun. Novel SCARA Welding Robot: China, 205798767U[P]. 2016-12-14.

[11] 曹峰, 刘积昊, 周宸, 等. 基于SCARA的五自由度焊接机器人的研究[J]. 机电一体化, 2015, 21(3): 9-12.

CAO Feng, LIU Ji-hao, ZHOU Chen, et al. Research on 5-DOF Welding Robot Based on SCARA[J]. Mechatronics, 2015, 21(3): 9-124.

[12] CLAUDIO U, JUAN C. Design, Construction and Control of a SCARA Manipulator with 6 Degrees of Freedom[J]. Journal of Applied Research and Technology, 2019, 17(2): 396-404.

[13] 刘凯, 开亚骏, 章林. 一种新型工业机器人设计及运动仿真分析[J]. 现代制造技术与装备, 2019(3): 56-57.

LIU Kai, KAI Ya-jun, ZHANG Lin. A New Industrial Robot Design and Motion Simulation Analysis[J]. Modern Manufacturing Technology and Equipment, 2019(3): 56-57.

[14] 董海涛, 武文革. 新型四轴码垛机器人机构设计与动力学仿真分析[J]. 包装工程, 2020, 41(3): 176-181.

DONG Hai-tao, WU Wen-ge. Mechanism Design and Dynamics Simulation of a New Four-Axis Palletizing Robot[J]. Packaging Engineering, 2020, 41(3): 176-181.

[15] 马春生, 张俊辕, 尹晓秦, 等. 新型串并联机构的运动学分析[J]. 包装工程, 2021, 42(13): 241-245.

MA Chun-sheng, ZHANG Jun-yuan, YIN Xiao-qin, et al. Kinematic Analysis of New Series-Parallel Mechanism[J]. Packaging Engineering, 2021, 42(13): 241-245.

Design and Kinematics Analysis of a New 6-DOF SCARA Robot

ZHANG Liang-an1, WANG Xiang1, XIE Sheng-long2

(1. School of Mechanical Engineering, Anhui University of Technology, Anhui Maanshan 243002, China; 2. School of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China)

The work aims to design a new SCARA robot with six degree of freedom to solve the inflexibility for the end of the traditional SCARA robot with four degree of freedom. Firstly, based on the analysis of the structural characteristics of the traditional four degree of freedom SCARA robot, the end structure was improved to increase the degree of freedom of the robot, so as to improve the flexibility of the end. Then, the forward and inverse kinematics models of this robot were established by D-H parameter method and algebraic method respectively. On this basis, the simulation analysis of this robot was carried out in the robotics toolbox of Matlab with the comparison method, and the correctness of the kinematics model was verified. Finally, the trajectory planning of this robot was studied based on the quintic polynomial interpolation algorithm. The experimental results showed that the trajectory, velocity and acceleration curves of this robot were smooth and continuous without any breakpoints and abrupt points. It indicates that the robot moves smoothly and has good kinematic performance. It lays a good foundation for the subsequent motion control of this robot.

SCARA robot; D-H parameter method; robot kinematics; quintic polynomial interpolation; trajectory planning

TB486；TP241.2

A

1001-3563(2022)19-0235-08

10.19554/j.cnki.1001-3563.2022.19.027

2021–09–26

政府间国际科技创新合作重点专项（2017YFE0113200）；国家自然科学基金（52205037）；浙江省基本科研业务费资助项目（2022YW43）

张良安（1981—），男，博士，教授，主要研究方向为机械设计、控制系统、自动化生产线、工业机器人。

谢胜龙（1988—），男，博士，讲师，主要研究方向为机器人原理与应用、数字孪生技术。

责任编辑：曾钰婵