简单复合体多重运动规律初探

董俊道

（哈尔滨理工大学理学院，黑龙江 哈尔滨 150080）

0 引言

探究短跑解析方法时，从相关的平动转动二维运动导出二维动能定理。关注测试图线、相关数据、生物特性，受能量按自由度均分原理启发，提出三四维动能定理。平动、转动反映了复合体刚体成分机械运动特点。耗散运动汇总了运动中非刚性成分导致的损耗。源动力运动涵盖转化为系统动能的各种因素，归纳总结出复合体及其多重运动模型。从而用多重运动替代初探短跑时提出的多维运动。依据跟拍测试原理和同步测试方法，归纳总结出多重运动专属的同步跟拍增量测试法。施于复合体总外力有综合作用，称此种合外力为体力。新模型、方法、认知，应用于力学领域简单复合体多重运动的测试、绘图、分析，初步实现了多重运动规律微元关系式的构建。

1 多重运动、简单复合体及同步跟拍增量测试法

（1）目前，多重运动涉及平动、转动、耗散运动、源动力运动四个机械运动重度。耗散运动为摩擦、粘滞、形变、潮汐等将动能转化为内能的运动形式；动力运动为电能、内能、生化能等转化为系统动能的运动形式。耗散运动形式、源动力运动形式不能视为运动维度，从而提出运动重度概念。这是引入机械运动重度的根本原因。

（2）简单复合体与体力。运动中复合体总质量不变，刚好具有平动、转动、耗散运动、源动力运动中二至四个运动重度的复合体为简单复合体。简单复合体易确定其质心，确定质心才能进行测试绘图分析。目前，多重运动理论研究对象是刚体为主的刚体、非刚体、动力机构等构成的简单复合体。简单复合体整体受的总外力有改变复合体整体运动状态的作用，称其为体力。本文探究这种体力与复合体质心运动的相关性。

（3）复合体机械运动中，其质心做多重机械运动，其中各重机械运动无优劣，无短板。

（4）同步跟拍增量测试法。“测量”指对象质心与摄像机主光轴相对位置的测量、对象质心与地或皮带（跑台测试）相对位置的测量（另一光电频闪拍测装置同步测量）及受力测量。“同步”即各量同时取值（电气联动）。“增量”指时间取增量，测试对象的位移等取增量。跟拍就是跟进拍摄。“拍”的意思是用频闪装置采集数据。调频电路调至某频率谐振，以此谐振频率拍摄测量。如拍摄频率为10 000 Hz时，时间增量误差小于万分之一秒。现代技术每秒可拍百万帧图像。可保证“增量”数据有足够有效数字。复合体多重运动用“同步跟拍增量测绘法”采集数据绘制图线。采集数据有四个要求：跟拍速度要测控的准；同步测力装置要测控的准（如用装有测力元件的垫、板等贴近同步测量）；频闪时间要测控准；各有效数据位数应匹配。同步测得量是密切相关量，能赖以精确运算、绘制精准描述各相关量关系的测试图线，以定量认知多重运动、构建复合体质心的多重运动规律。

2 简单力学复合体多重运动规律的测试与构建

2.1 一例二重运动复合体质心的位移时间增量图线

一长方厚木板质量为m，推动装置使木板以水平初速度v沿水平滑道运动，请说明撤掉推力木板如何运动。目前这类问题通用解法，是在手册上查到相关摩擦系数，然后解析。这种方法只是粗略估算，目前尚不能即时准确解析。厚木板以惯性滑行时，做耗散运动、平动二重运动。运用下述装置可即时测量、绘制图线、分析。（a）置于滑道上表面的测力装置测量木板滑动时的水平摩擦力f（取值频率受摄像机控制。测力装置输出有高频成分，须加滤波器），绘出图1所示ot轴线下部的图线。（b）水平滑道旁平行轨道上，有可调速跟拍高速摄像机（跟拍摄像拍摄频率倒数为△t），撤掉推力瞬间以速度v跟拍。跟拍木板质心相对摄像机主光轴的位移增量。（c）木板质心正上方装竖直向上发光激光管及可调频闪光电拍测装置（其频闪情况受摄像机控制）。通过其上部有机玻璃尺（架于地上）观测木板对地水平位移增量。（d）各测量装置在高速摄像机控制下联动同步测量，每间隔△t同步记录一次，使每个△t对应一段位移增量。测量记录的量还有：开始的第一个△t秒末记为t，下个△t秒末记为t……见图1。（e）高速摄像机以速度v跟拍时，主光轴运动图线是xk。如果跟拍中木板与滑道无摩擦，木板质心的位移图线也是xk。（f）图中（x，t）为绘制木板损耗位移增量图线起点。跟拍中随时间推移木板质心相对前一位置损耗的位移增量顺次等于△x=xs、△x耗=Cs、……，依此系列增量数据给出的位置，绘制出木板损耗位移增量时间图线xA。（g）激光拍测的参考点为（0，t）（对地）。平动增量△x=ts-tx=xs、△x=ts-ts=Cs……系列（负）增量顺次等于激光拍测装置在t时段、t时段……的系列平动位移增量，于是绘出木板水平平动位移增量时间图线xA（与前者重合）。（h）图1向下各矢量的参照物是主光轴，向上各矢量的参照物是固定于地上的标尺。图线xA与xk之间（xA上部）为耗散区域，xA与下部0t之间为平动区域。从上部看曲线xA是耗散位移增量时间图线，从下部看曲线xA是平动位移增量时间图线。曲线xA的两面性，保证了同一时段不同运动重度对应的位移增量等值。（i）不论摩擦偶如何变化、xA斜率如何，上一条的表述不变。

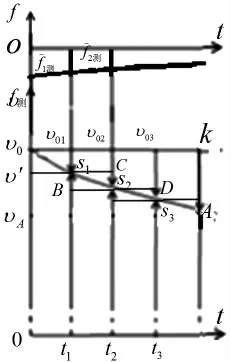
图1 二重位移增量图线

为了使潜水艇、鱼雷、潜航器等更好在水中水平滑行，笔者探究它们外形与所受摩擦粘滞阻力对速度影响的水平测试是二重运动测试（潜入测试可保证测试对象与水接触面积不变）。驱动一飞轮匀速转动，脱离驱动装置瞬间开始正式同步增量测试：依飞轮边缘标志点推算损失的线位移绘制图线。依轴承处测力装置给出阻力矩时间图线，飞轮依惯性做的减速转动是转动与耗散运动二重运动，亦可绘制二重运动图线。

2.2 二重动量定理与二重动能定理的微分表达式的构建

图2 二重速度增量图线

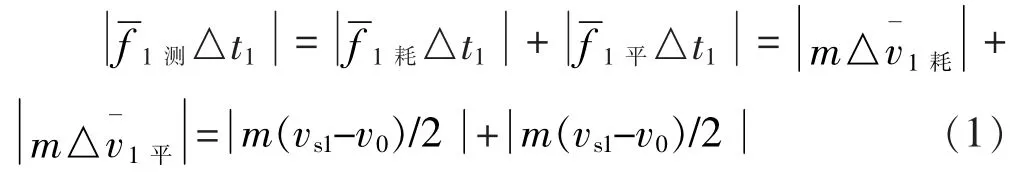
其中，（v-v）可表述为（v-v）（h）同理对第二小段冲量动量的增量为：

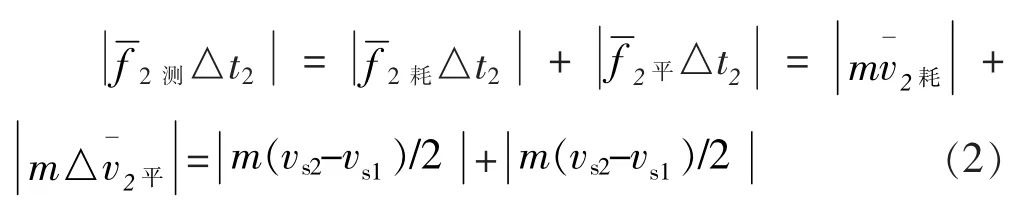
（v-v）可表述为（v-v）……（i）于是任意时段木板二重运动动量定理微分表达式为：

（j）二重运动动能定理微分表达式的推演。式（3）可简化为：

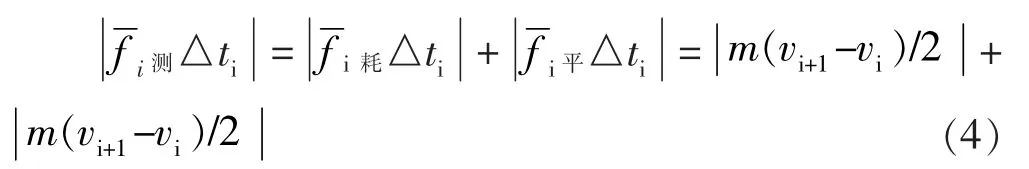
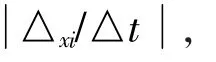
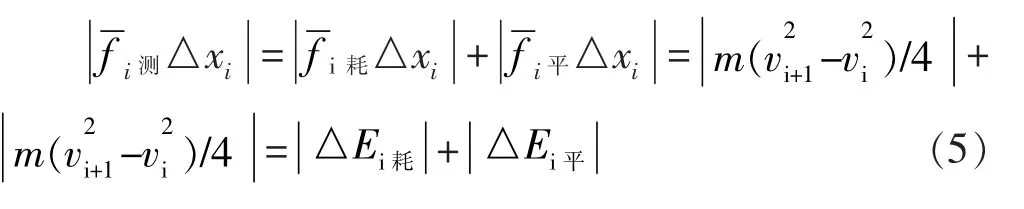
2.3 老年车滑行测试与质心三重位移增量图线

四轮老年车相当于在座椅上装车轮，系简单复合体。质量为m的老年车以初速度v沿平直路面进行滑行测试。滑行时车辆复合体质心做耗散运动、平动、转动三重运动。测试方法与木板滑行测绘原理步骤相同。在车上装一竖直细管，其中线过车辆质心。细管下面装激光频闪光电拍测装置，车下路面有刻度尺，拍测车辆对地平动位移增量。频闪间隔为△t。车辆速度为v时，有v=0x/△t=5.00 m/s，0x=△t×5.00 m/s。安装在地面上的测力装置同步观测车辆受的总水平阻力（水平体力），绘制如图3所示的上部ot轴下面的阻力时间曲线。阻力时间图线下面的运动图象有三个象限：xxk、xA和x0A。0A代表对地速度为0的水平线。老年车做无滑动无动力滑行时，相对老年车前进方向，轮下缘对质心（与轴心同速）的线位移为负值，线位移增量时间图线xA与平动位移增量时间图线xA以0A为对称轴呈镜像关系。线位移增量时间图线在0A下方。见图3x0A。如车辆无位移损耗，频闪光电拍测装置拍测的质心位移图线为xk。以速度v同步跟拍测量，t、t等时刻主光轴在xk上的位置顺次对应为x、x……有损耗时，老年车损耗位移增量顺次为△x=xs、△x=Cs、……可绘制类似图1上部损耗位移的增量时间图线，见图3xA。从0A下侧向上看图线xA是平动位移增量时间图线。t、t……各时刻，老年车对地平动位移增量、损耗位移增量、线位移增量间的数值关系顺次为△x=ts-0x=xx′=xs-0=△x=ts′-0x=Ex=△x……

△x=ts-ts=Bs=Cs=△x=ts′-ts′=Gs′=△x……电动车复合体依惯性前进（滑行）时，其质心做耗散运动、平动、转动三重运动。位移增量图线xA的两面性及xA与xA的镜像关系，保证了同一时段三重位移增量等值。第三重运动图线xA不具两面性（耗散区域没有镜像）。故不涉及xA下边区域。一般车辆依惯性滑行时位移图线与图3类似。如车轮变小或有人乘车时，阻力变大，xA与xA的斜率同步变大。

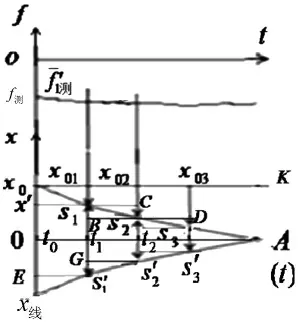
图3 老年车位移增量图线

2.4 老年车三重运动规律微分表达式的构建

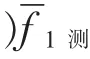
图4 老年车速度增量图线

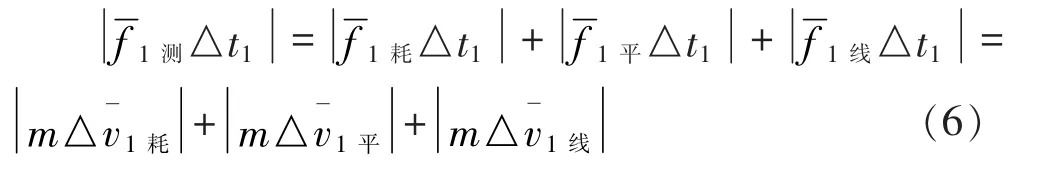
任意时段的老年车三重运动动量定理微分表达式为：

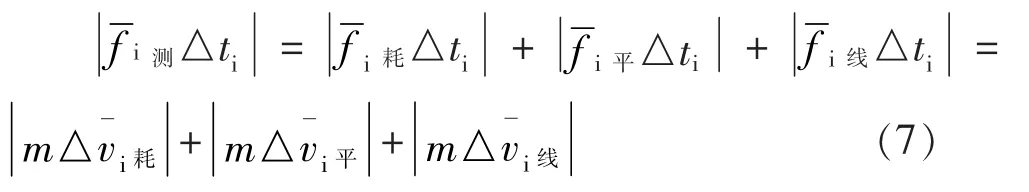
（i）三重动能定理微分表达式的推演。式（7）可转化为：

（j）依式（5）的推导，易推得任意时段老年车水平向三重动能定理的微分表达式为：

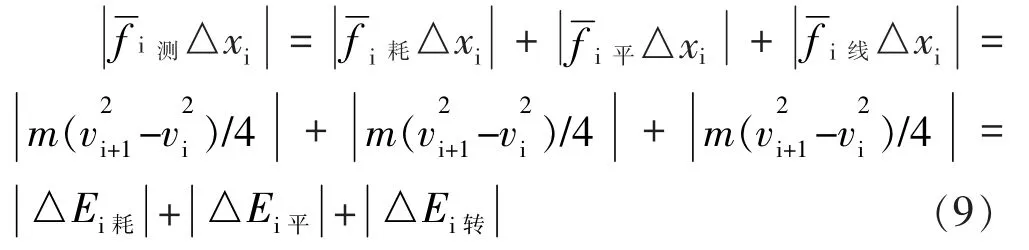
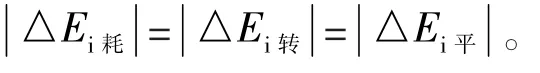
2.5 滚摆运动分析

学过普通物理的都见过滚摆运动，但都未解过相关习题，因为尚不知其运动规律。

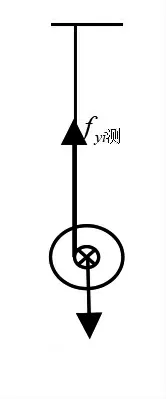
图5 滚摆

2.6 一例源动力参与的多重运动

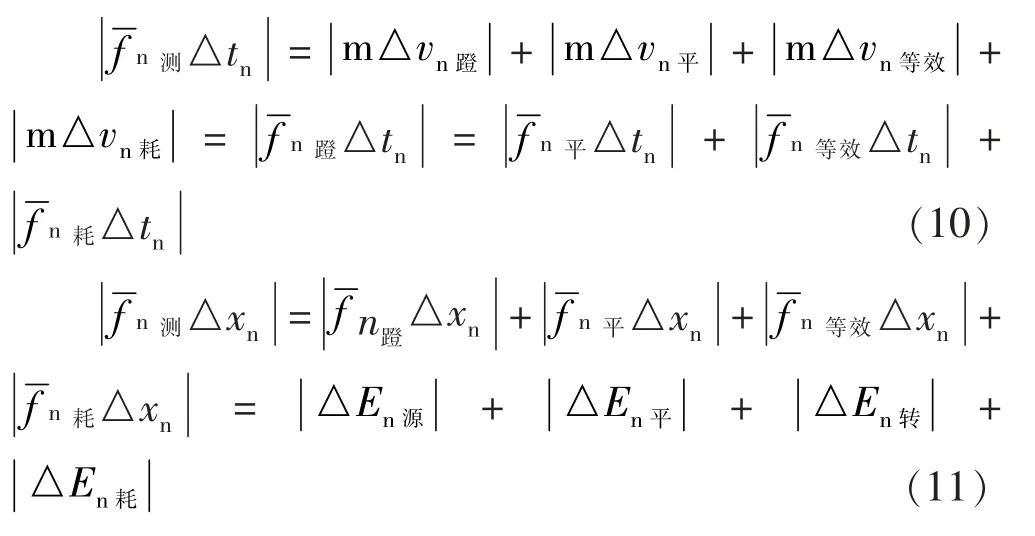
（d）本小段叙述涉及的运动重度排序，与图6标注的1、2、3、4顺序同。（e）短跑的tts时段的运动称为过渡阶段。图6首次揭示短跑过渡阶段是运动员转动贡献位移。（e）运动员质心的推算。目前，依运动生物力学教材提供的环节参数、回归方程，可结合伐里农定理求解人体质心。但只适用于直立、两臂下垂竖直站立、端坐或某些特殊姿态的人体。因为一般情况下运动员各环节决定的线段不共面，目前尚无推算运动中运动员质心位置的一般方法。这是当前急需解决的问题。

图6 复合速度图线与关联分析

2.7 简单复合体多重运动的几点说明

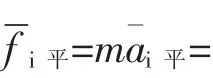
3 初步结论

（1）对组合体整体运动构建复合体模型、多重运动模型及体力概念，这是探索复合体运动规律第一步。

（2）归纳提炼出的同步跟拍增量测试法是探究复合体整体多重运动的专属测试方法。

（3）同步跟拍增量测绘法、复合图像表述法是揭示复合体整体运动规律的可行方法。

（4）用同步跟拍增量测试法测试，绘制复合体质心位移增量时间图线、速度增量时间图线，可构建复合体多重运动规律。和无须构建新维度。运动维度与运动重度是含义不同的概念。

（5）多重运动规律是在其相互作用系统中用同步跟拍增量测试分析法构建的运动规律。

（6）牛顿第二定律表明，某时段质点（或刚体质心）受合力△F¯作用时有△F¯=m△a。复合体受的合外力称为体力。体力作用下复合体做二三四……重运动，遵循多重运动规律。复合体可视为质点时，多重运动规律化为△F¯=m△a。

（7）文中探讨的多重运动是近地多重运动，是探究狭义多重运动的初期阶段。

几十年前就有力学工作者对短跑运动进行整体观测，首次得到短跑测试图线，已具备全面解析途中跑运动的条件，但未能解析。因为未构建复合体及多重运动模型。长期探索这一实验成果，用多重运动规律能成功分析短跑水平运动，已系拓展经典力学的尝试。用于分析力学复合体运动问题，进一步拓展经典力学研究范围，有必要检验深究。检验深究之前，探讨频闪拍摄记录法的配合技巧、误差分析很关键。因为只有精准地测量结果才有说服力。