GeoGebra软件在高中数学课堂中的应用——以“圆锥曲线”教学为例

李琨

广东省中山市小榄中学 528415

随着时代的进步，信息技术逐渐走进了高中数学课堂，信息技术与数学的融合有效地打破了机械化、程序化、单一化的教学模式，为数学课堂注入了新的活力.GeoGebra（以下简称GGB）软件可以生动化、过程化、形象化地呈现知识的形成过程，有助于调动学生学习的积极性，让学生在一个更为广阔的空间里去发现、去总结，进而拓展学生的知识面，拓宽学生的视野，提高教学效率.

为了突破圆锥曲线这一教学难点，教师不断地做了各种尝试，如结合实物模型让学生观察，通过动手实验让学生体验运动过程，然因高中生的空间思维能力较弱，所以大多数学生并未形成这种空间意识.随着多媒体技术的发展，几何画板走进了数学课堂，虽然应用几何画板可以动态地呈现圆锥曲线形成的过程，但是它不能让学生更加直观地感受图像随着曲线方程变化而变化的过程.另外，几何画板制作教学课件的过程较为烦琐，而高三数学教学的时间紧、任务重，教师的时间和精力有限；同时，因其操作复杂，对于一些年纪大的教师来讲也是一种压力.可见，其并不是一种高质、高效的手段.而GGB软件的操作简单，它的出现为数学教学带来了巨大便利［1］.基于此，笔者分析了圆锥曲线的地位、价值及教学现状，并浅谈如何借助GGB软件高效完成圆锥曲线教学目标，以期共鉴！

圆锥曲线的地位及价值

圆锥曲线是高考中的核心考点，每年都有20分左右的题目与其直接相关，可见其在高考中的重要地位.圆锥曲线中的三种曲线形成了一个完整的知识体系，从定义、方程、性质及应用中都蕴含着丰富的数学思想，尤其数形结合思想在整个体系教学中有着重要的应用，方便学生将函数、向量等知识联系在一起，进而帮助学生完成知识的内化及知识体系的建构，方便学生更加全面、更加系统地掌握数学的基本内容.同时，因三种曲线紧密相连，可引导学生利用椭圆的学习经验自主完成其他两种曲线（双曲线和抛物线）的学习，通过对比、交流、探究，深入理解和掌握三者的区别和联系，进而培养学生自主学习能力.

由此可见，学好圆锥曲线不仅有利于高考数学成绩的提升，而且有助于数学思想和数学素养的提升，因此教学中必须采用更加高效和高质的教学手段帮助学生克服圆锥曲线学习过程中遇到的困难，以此提升学生的学习能力.

圆锥曲线教学现状分析

高中教师知晓本章内容在整个高中数学教学中的地位，也非常重视本章内容的教学，然其教学方法依旧延续着传统的“灌输”教学模式，教师讲解时并未结合学情进行教材和教法的钻研，而是终而复始地重复着原有的教学方法，这样的课堂是枯燥和乏味的，难以激发学生的学习热情，自然不利于学生思维能力的培养.同时，部分教师在教学中习惯照本宣科，不重视教学过程，未能将信息技术与数学课堂完美地融合起来，没有激发学生学习的积极性，学生自然对知识的理解也无法深入.另外，按照大纲要求，本章内容规定的课时较少，部分教师认为若教学中过多地进行过程演示可能会浪费宝贵的课堂时间，也会占用练习的时间，若没有足够的练习学生更难以理解.可见，“题海”思想在教学领域中还占有统治地位.然若没有过程的讲解，学生对知识的理解将过于概念化，缺乏应变能力，这样面对难度较大、计算较复杂的题目时容易产生心理负担，影响学生学习的信心.

可见，圆锥曲线教学中存在着一些不足，教学中必须顺应时代的发展，发挥好信息技术的巨大优势，让学生在知识的动态生成中去感悟和探究，从而提高学生的学习兴趣.

GGB软件引入的价值

基于圆锥曲线在高中数学中的地位及教学中存在的不足，教学中应作出一些改变.经教学实践发现，借助GGB软件来制作圆锥曲线教学案例可以实现化抽象为具体的效果，不仅可以节省时间，而且通过动静结合可以打破学生对定义、性质的理解只能靠死记硬背来完成的尴尬局面，学生可以借助动画去观察、分析、总结，让学生在动态变化中寻找规律，找到解决问题的方法，这样对学生理解和应用相关知识具有不可估量的作用［2］.同时，GGB软件的操作简单，只要拖动构图的元素，图像就会随着元素位置的变化而发生形变，有助于学生通过直观观察来体会从特殊到一般的过程.借助GGB软件引导学生通过观察、对比、分析、总结几何图形的性质，不仅能加深学生对相关知识的理解，而且使学习变得更有画面感，更能激发学生的学习兴趣，有助于师生突破圆锥曲线这一教学难关.

GGB在圆锥曲线教学中的应用

限于篇幅，笔者以椭圆教学为例，展示了GGB软件的应用价值，以期改变教学现状，让学生学得更加轻松和愉悦.

1.教学目标

（1）知识与技能：①椭圆定义；②推导椭圆的标准方程.

（2）过程与方法：①借助GGB软件展示模型，让学生自己完成定义的总结和归纳；②利用GGB的运算功能，让学生借助数形结合推导出椭圆的标准方程.

（3）情感与价值观：①通过直观观察和数学语言抽象，培养学生的直观思维和数学语言应用能力；②在过程中渗透数形结合思想和坐标法，以培养学生的数学素养，提升学习能力.

2.教学重难点

教学重点：椭圆的定义及标准方程.

教学难点：推导椭圆的标准方程.

3.教学过程

师：在生活中经常会看到如图1所示的椭圆形建筑，请大家想一想，在生活中你还看到了哪些椭圆呢？（教师用PPT展示图1）

图1

通过PPT的展示和生活中实物的联想创建一个和谐的教学环境，为接下来的探究做好铺垫.

师：请观察图2，你发现了什么？（教师运用GGB软件进行圆锥曲线形成展示，引导学生通过观察发现规律）

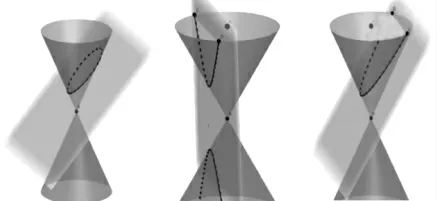
图2

生1：若用一个平面来切割圆锥，平面的角度不同，切割出的曲线也不同.

师：很好！这三种曲线就是本章学习重点.（教师借助GGB软件的直观性，让学生对圆锥曲线章节内容有一个整体认识，从而培养学生的整体意识，为后期的对比研究做好铺垫）

师：在圆锥中放2个球（如图3所示），一平面与两球相切，猜想一下平面截圆锥面所得曲线会是什么图形呢.

图3

教师利用GGB软件将双球模型重新展现，学生仔细观察图形并结合图2容易得出该截曲线为椭圆.通过动态观察，激发学生的好奇心，高效引导学生进入椭圆定义的探究.

为了进一步探究椭圆的定义，在截曲线上任取一点P，过点P作圆锥的母线交小球于点A，连接PA，引导学生猜测PF1与PA的长度关系.学生大胆地猜测两者的长度相等，教师并未急于给出答案，继续利用GGB软件让学生过球外一点G作球的切线.如图4所示，任取四条切线，切点分别为C，D，E，F，根据与圆的切线相类比，利用GGB软件的测量功能容易得出GC=GE=GD=GF，于是学生顺利地得出PF1=PA.同理，学生过点P作圆锥的母线，其与大球相交于点B，可得PB=PF2.当引导学生探究的和为定值时，教师又利用GGB软件引导学生观察动点P的运动过程，随着动点P的变化，PF1，PF2的长度也随之发生了变化，然的值却未改变，进而借助GGB软件动态呈现了椭圆的定义生成过程.

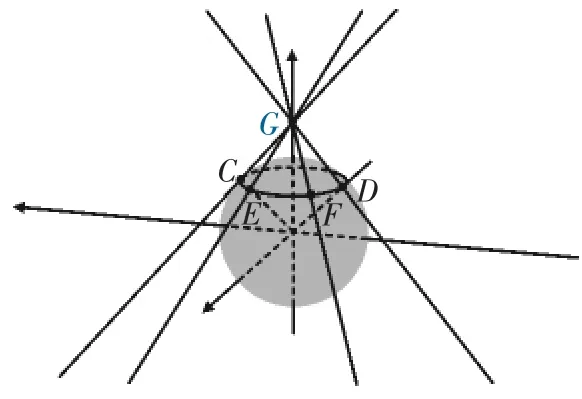
图4

学生掌握了椭圆的几何定义，教师可以引导学生从“数”的角度继续探究，进而得出椭圆的标准方程.以F1F2所在的直线为x轴，以F1F2的中垂线为y轴，建立直角坐标系，设点P（x，y），F1（－c，0），F2（c，0），利用两点的距离公式可得=2a.显然，若对该方程进行化简需要较长的时间，虽然教学中鼓励学生多观察、多动手，然其并不违背直接应用前人的已有经验，因此化简时可以利用GGB的运算功能来完成，这样求解过程清晰可见，有利于课堂效率提升［3］.

这样，在教学中应用GGB软件不仅可以让学生在动态变化中理解概念定义的生成过程，而且可以借助其运算功能使学生从复杂的运算中脱离出来，避免学生仅重视标准方程的推导而忽视对椭圆定义的理解.可见，利用GGB软件能有效化解教学的重难点，能减轻学生的运算负担，提高课堂效率.