非厄米系统中单粒子波包的动力学行为

姜雅金，姜润泽，张禧征

（天津师范大学物理与材料科学学院，天津 300387）

近年来，随着量子力学应用研究的迅速发展，人们已经能够通过量子模拟手段，即利用人工可调控的量子系统，去模拟待研究的量子系统，探究当前实验条件下难以观测和解释的物理现象.例如用光晶格与耦合腔阵列[1]等系统来模拟传统凝聚态物理中的强关联系统，最终在这些可控系统中达到制备、传输和控制量子态的目的.在制备、传输和控制量子态的过程中，人们已经完成了对厄米体系中粒子在化学势作用下动力学行为的基本运算和分析.

当Bender[2]提出狄拉克厄米性并非实数能谱和幺正的时间演化的必要条件时，研究者们发现系统哈密顿量中的相互作用势还可以由实数域延扩到复数域，且不改变其能谱的实数性.因此，非厄米系统引起了人们的广泛关注.非厄米系统是用来描述万物间相互联系、相互作用的真实物理系统，将等效的非厄米哈密顿量引入后，能够更加简单直接地描述出外部环境对研究者所关心系统的影响，但非厄米系统中的单粒子波包在紧束缚模型上发生散射时存在共振穿透现象.所以，研究人员对“是否可以将这种共振穿透现象作为理论基础，对非厄米系统中的紧束缚模型进行特殊的结构设计来实现单通性系统的制备”这一问题进行了深入思考.

本研究主要以无限长的单链为基础，通过调控非对称耦合腔内虚数势[3]及腔内格点间不等幅跳跃，观察并分析单粒子波包入射至非厄米散射中心后在特定参数下实现的信息单向输运[4]，旨在为量子信息的输运提供理论基础.

1 方法

1.1 计算方法

量子力学以波函数公设、微观粒子动力学公设和算符公设等几个基本假设为起点.由于厄米算符的本征值为实数时即为可观测量，因此，算符公设必须用厄米算符来表示量子力学中的力学量.描述真实物理系统时，由于厄米哈密顿量用于表示系统的能量，其本征值为实数，因此必须满足厄米性.从物理角度分析，满足厄米性的哈密顿量描述的是封闭的物理系统，但无论生活中还是研究中，完全封闭的物理系统趋于理想化.因此，本研究仅对非厄米系统中的一维紧束缚模型展开分析.此外，经电子源产生单电子脉冲，带电粒子入射到一维紧束缚链上，将在每个格点能量最低的能带上发生跃迁.根据紧束缚近似原理，总有单电子在近似情况下可通过能带间的带隙发生隧穿效应.同时，由于带隙足够大，处于低能级的带电粒子很难跃迁至上一能级，因此可近似认为此过程中没有能量损耗.本研究将在该理论基础上对单粒子波包进行探究.

首先，假设一条长度为无穷大的一维紧束缚链，晶格均匀排列分布于该链上，在N=0的位置上存在虚数势

对于非厄米系统，虚数势是一种由于系统与外界环境耦合而产生的在位势，一般用iγ来表示，同时格点间跳跃常数为-J，如图1所示.

图1 存在虚数势的一维紧束缚链Fig.1 One-dimensional tight binding chain with imaginary potential

图1为具有缺陷的一维紧束缚链，可采用Bethe Ansatz方法求解，得到系统的哈密顿量

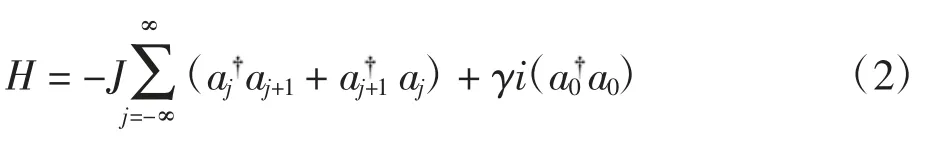
设公式（2）中哈密顿量满足本征值方程

公式（3）中：Ψ为哈密顿量H的本征态，满足

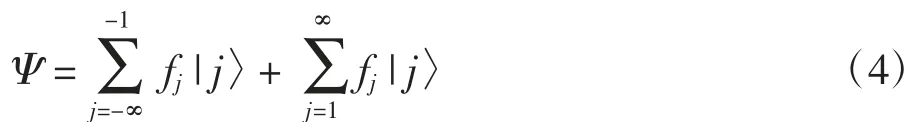
由于势的影响，位于N=0处的尝试波函数可由相邻格点间的公式给出.

将公式（4）代入公式（3）可得

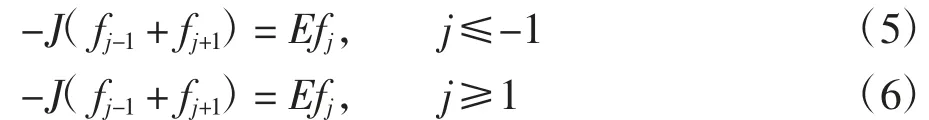
令尝试波函数

满足公式（2）哈密顿量的非厄米系统中，相邻格点间存在相互作用，且在虚数势的影响下，得到波包由左向右入射后（规定向右为正方向），行进过程中遇到N=0处的非厄米散射中心时，会发生奇特的散射现象，因此将尝试波函数fj代入公式（9）—（11），得到左入射时单粒子波包在虚数势影响下的透射系数tL和反射系数rL分别为

则透射几率T和反射几率R可以表示为

最后，在公式（2）哈密顿量的作用下，单粒子波包的能级光谱可以表示为

1.2 图像分析

由公式（12）和公式（13）可知，反射系数与透射系数只依赖于波矢k、跳跃常数J与虚数势实部γ，与系统的长度N以及势所处的位置Nc无关.为了能够观察单粒子波包的反射几率和透射几率受γ影响的变化规律，作数值解，如图2所示，其中波矢k=π/2，跳跃常数J=1.由图2可知，对于满足公式（2）中哈密顿量的非厄米系统而言，系统中的散射中心带给波包的影响非常显著.传播过程中，单粒子波包遇到虚数势时会发生一定几率的透射和反射，并且随着γ的增大，反射几率R与透射几率T也增大，递增程度如图2所示.这说明满足公式（1）的非厄米散射中心带给系统的影响可以类比于从外界接入一个通道并注入能量，使散射中心处粒子的透射行为和反射行为增强（γ＞0），本研究将这样的系统认为是增益的.

图2 γ＞0时反射几率和透射几率受γ影响的变化规律Fig.2 Changing law of reflection probability and transmission probability affected by imaginary potential γ when γ＞0

取系统长度N=100，虚数势位于系统中央，即Nc=50处，利用数值法模拟宽度ω=1/3的单粒子波包在空间内的演化规律，结果如图3所示.从图3可以看出，初始位置N0=10处的单粒子波包在Nc处受虚数势的影响分裂为反射波与透射波，其中，波矢k=π/2，跳跃常数J=1，γ=0.8.

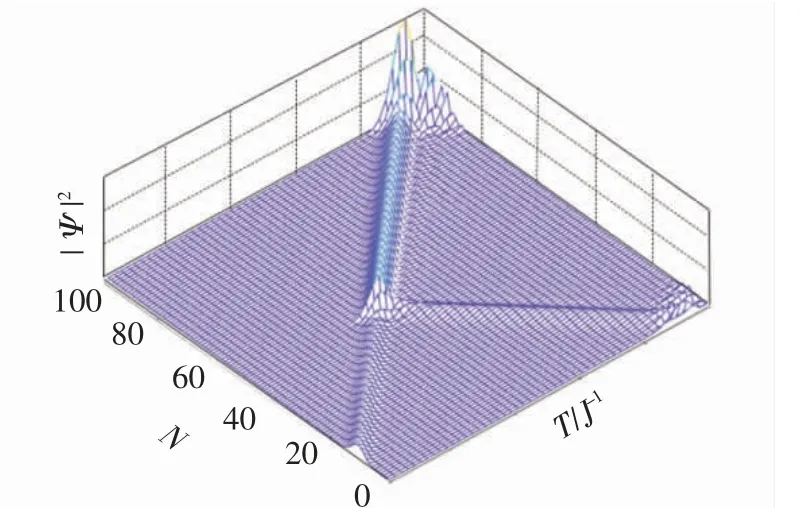
图3 单粒子波包的演化示意图（Nc=50，N0=10）Fig.3 Evolutionary schematic of the single-particle wave packet（Nc=50，N0=10）

此外，单粒子波包之所以能够不散传播，主要是因为运动的高斯波包[5]在任意大小的φ值条件下，都能够保形并且匀速地进行传输，其中φ决定了群速的大小即波包演化速率正比于sin φ.然而φ值大小不同的高斯波包对波包的半宽也有不同的要求.从高效、局域传输的角度考虑，取φ=π/2最为理想[6].

同理，利用Bethe Ansatz方法精确求解哈密顿量本征值及粒子的散射，可以得到单粒子波包在γ＜0时的透射系数tL和反射系数rL

由此可得反射几率R和透射几率T受γ影响的变化规律，结果如图4所示，其中，波矢k=π/2，跳跃常数J=1.

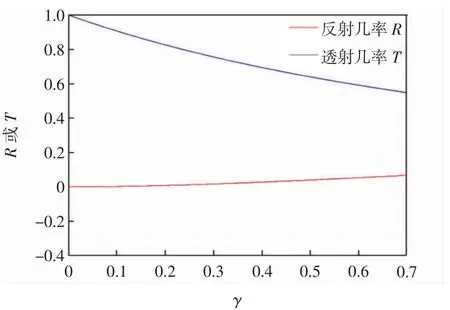
图4 γ＜0时反射几率和透射几率受γ影响的变化规律Fig.4 Changing law of reflection probability and transmission probability affected by imaginary potential γ when γ＜0

满足公式（1）的非厄米散射中心带给系统的影响可以类比于系统向外界搭建一个通道输出能量，即向外界耗散掉一部分系统能量[7]，使得散射中心处粒子的透射行为和反射行为被削弱（γ＜0）.然而由图4可以看出，随着γ的递增，虽然透射几率呈衰减状态，但反射几率却不减反增，这是因为波包在传输过程中产生了干涉效应[8]，导致系统的反射几率由于干涉相长而呈微弱的递增现象，但整个系统还是可以看成是一个耗散系统.

综上所述，量子散射过程是测量仪器与被测系统形成理想纠缠的过程[9]，被测系统所处的状态直接影响紧束缚模型中电子空间波函数的反射和透射.当系统中接入一个γ＞0的通道使其转化为增益系统时[10]，其反射几率R和透射几率T均随γ的增大而增大，散射行为增强，可将其视为一个“源”[11]；同理，当接入一个γ＜0的通道使其转化为耗散系统时，散射行为被削弱，可将其视为一个“漏”[12].然而，当离散量子系统中同时引入两个正负相反的虚数势，且格点之间被调制为不等幅跳跃结构时，单粒子波包就产生了奇特的散射现象.

2 单通性系统

2.1 非对称耦合散射中心

在研究单通性系统的构建前，首先要对散射中心内引入虚数势和不等幅跳跃的一维紧束缚链进行讨论.假设一条长度为无穷大的单链，晶格均匀排列分布于链上，N=0和N=1位置上的虚数势分别为iγ和-iγ（γ＞0），且双虚数势所在的格点间存在不等幅跳跃-α和-β，由此可视为将孤立的紧束缚系统引入了含有虚数势的非对称耦合散射中心，如图5所示.

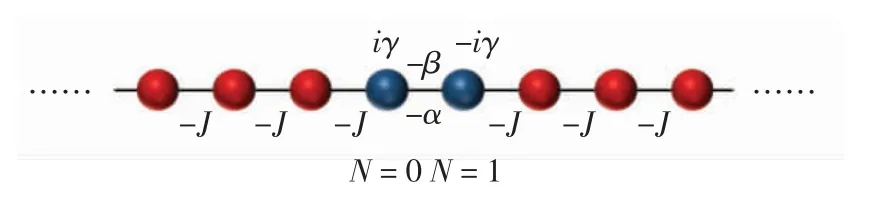
图5 存在虚数势和不等幅跳跃的一维紧束缚链Fig.5 One-dimensional tight binding chain with imaginary potential and unequal amplitude jumping

图5中，系统的哈密顿量为

由于双虚数势的引入以及非对称耦合结构对系统的影响，同样利用Bethe Ansatz方法可以在非对称耦合散射中心处得到与公式（9）—（11）略有差别的下列公式

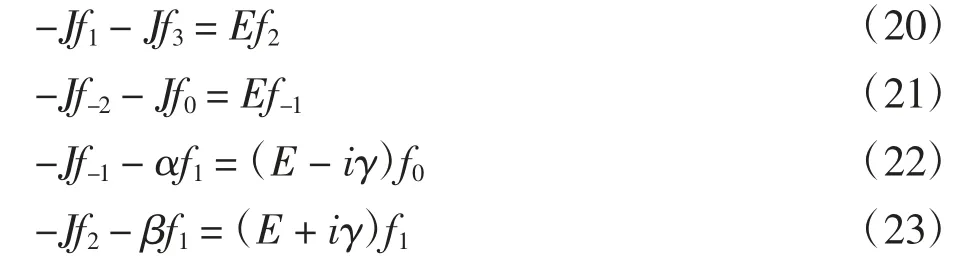
在满足公式（19）哈密顿量的非厄米系统中，单粒子波包由左向右入射后（规定向右为正方向），遇到含有双虚数势的非对称耦合散射中心时，波包会发生散射，将尝试波函数fj代入公式（20）—（23），最终可以得到透射系数tL和反射系数rL

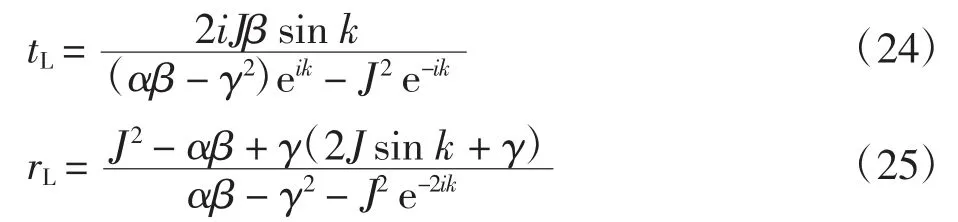
经计算可知，反射系数与透射系数不仅依赖于波矢k、跳跃常数J与虚数势实部γ三者间的比值，还与系统中非对称耦合散射中心处不等幅跳跃α和β的大小密切相关.图6为反射几率R与透射几率T受参数α、β和γ影响后的变化规律.

由图6（a）可知，随着虚数势中γ的增大，系统的透射几率T逐渐增大，反射几率R逐渐减小，透射行为更加明显.说明单粒子波包从左向右入射至紧束缚链上，由于不等幅跳跃α=2和β=3，即α＜β，粒子透射的能力强于反射能力，所以表现为透射几率随着势的增大而增大，反射几率随之减小.因此，在双虚数势±iγ作用下，系统中粒子的透射现象更明显.

由图6（b）可知，随着不等幅跳跃α的增大，系统的透射几率T逐渐减小，反射几率R逐渐增大.对于从左入射的单粒子波包而言，系统中不等幅跳跃α表示着波包经过散射中心后反射回到原路径的困难程度，α的数值越大，单粒子波包反射的能力越强，粒子的反射现象更为明显.

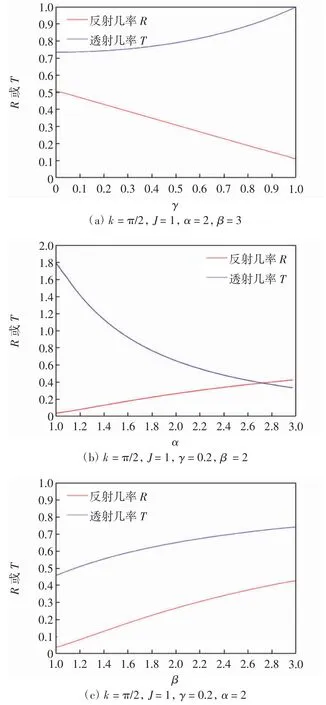
图6 单粒子波包由左入射时，反射几率和透射几率在不同参数作用下的变化规律Fig.6 Changing law of reflection probability and transmission probability under the action of different parameters when the single-partical wave packet incident from left

对于从左入射的单粒子波包而言，系统中不等幅跳跃β表示波包经过散射中心后按原路径透射的困难程度，β的数值越大，单粒子波包透射的能力越强，透射几率越大，反射几率越小.然而由图6（c）可以看出，随着不等幅跳跃β的增大，透射几率逐渐增大，反射几率非但没有随之减小，反呈递增的状态，这是由于干涉效应，即相位的干涉相长导致了反射振幅的异常变化，表现为反射行为和透射行为均增强.

取系统长度N=100，且假设虚数势位于系统中Nc=50和Nc=51处，利用数值方法模拟宽度为ω=1/2的单粒子高斯波包在空间内的演化规律，其中，波矢k=π/2，γ=0.2，跳跃常数J=1，不等幅跳跃分别为α=2和β=3，结果如图7所示.

图7 单粒子波包的演化示意图（Nc=50、51，N0=10）Fig.7 Evolutionary schematic of the single-particle wave packet（Nc=50、51，N0=10）

由图7可知，随着时间推移，波包从格点为N0=10的初始位置开始行进，行进过程中在Nc=50和Nc=51处遇到散射中心±iγ.此后，波包分裂为反射波和透射波，一部分按原定方向继续前进，另一部分按与入射方向相反的路径返回.

当单粒子波包从链端的反方向入射，即由右向左入射时，利用Bethe Ansatz方法继续精确求解公式（19）哈密顿量的本征值及粒子散射.

首先，设尝试波函数为

将尝试波函数fj分别代入公式（20）—（23），最终得到单粒子波包右入射时在该非对称耦合散射中心影响下的透射系数tR和反射系数rR

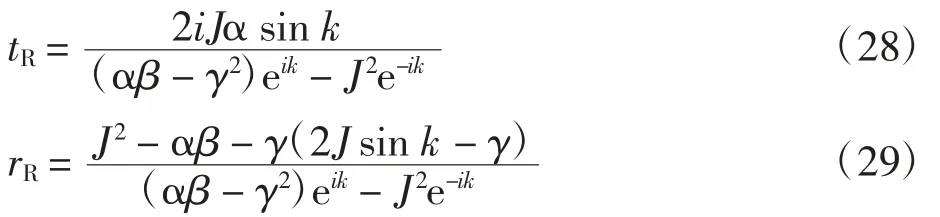
其反射几率R和透射几率T受不同参数α、β和γ影响的变化规律如图8所示.

由图8（a）可知，随着虚数势中γ的增大，系统的透射几率T和反射几率R均逐渐增大，且反射行为更明显.说明单粒子波包从右向左入射至紧束缚链上，由于不等幅跳跃α=2和β=3，即α＜β，粒子的反射能力强于透射能力，表现为反射几率处处大于透射几率.因此，在双虚数势±iγ作用下的系统中，粒子反射现象更为明显.

由图8（b）可知，随着不等幅跳跃α的增大，系统的透射几率T和反射几率R均逐渐增大，且透射行为更明显.对于右入射的单粒子波包，系统中不等幅跳跃α表示波包经过散射中心后按原路径透射的困难程度，α的数值越大，单粒子波包透射的能力越强，透射几率越大.然而图8（b）中粒子的反射几率非但没有减小，反而越来越大，这是由于干涉效应，即相位的干涉相长导致了反射振幅的异常变化，表现为反射和透射行为均增强.

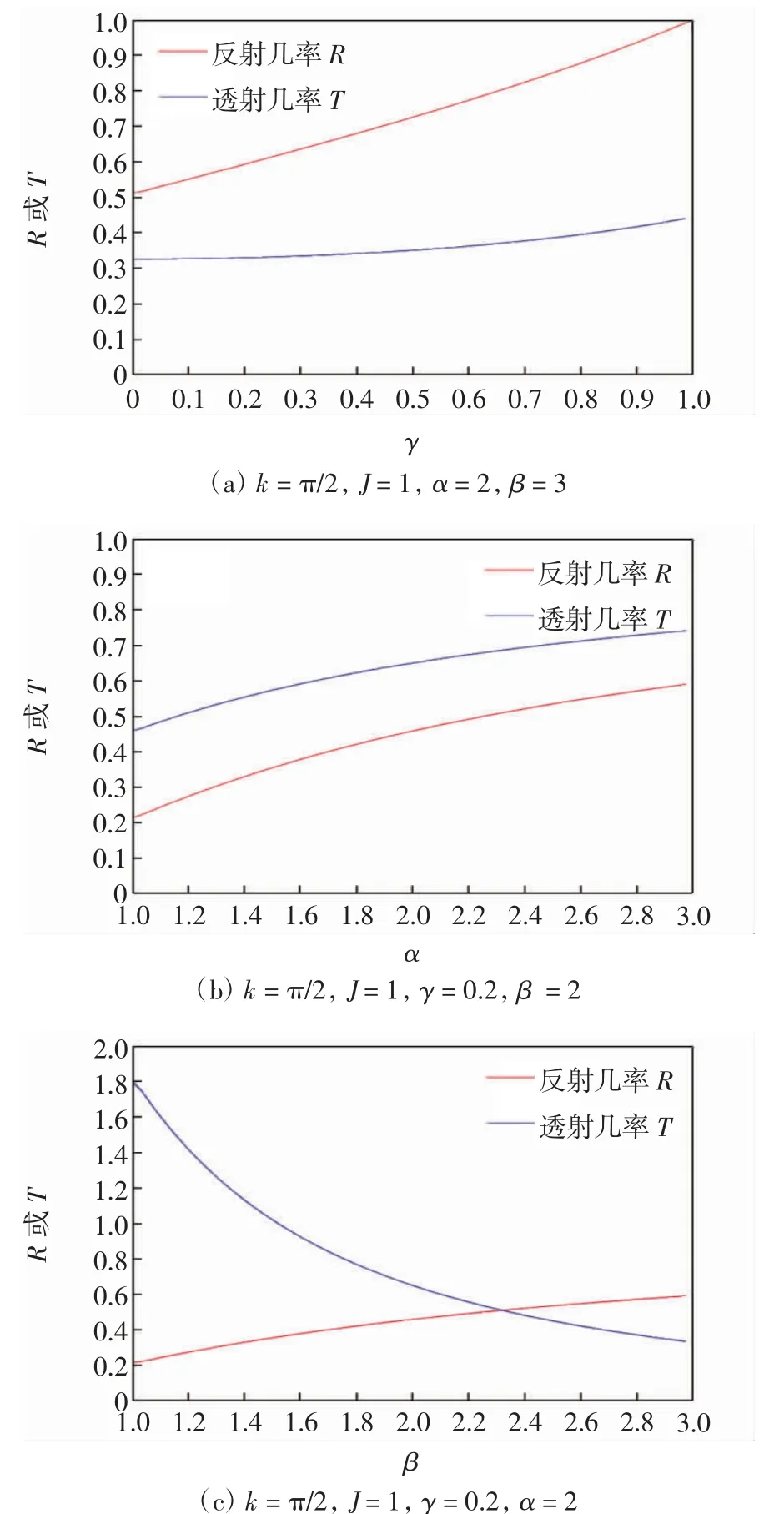
图8 单粒子波包由右入射时，反射几率和透射几率在不同参数作用下的变化规律Fig.8 Changing law of reflection probability and transmission probability under the action of different parameters when the single-partical wave packet incident from right

由图8（c）可知，随着不等幅跳跃β的增大，透射几率T减小，反射几率R增大，反射行为更明显.说明对于从右向左入射的单粒子波包，系统中不等幅跳跃β表示波包经过散射中心后反射回到原路径的困难程度，β的数值越大，单粒子波包反射的能力越强，反射几率越大.

取系统长度N=100，假设虚数势位于系统中Nc=50和Nc=51处，利用数值方法模拟宽度为ω=1/2的单粒子波包在空间内的演化规律，其中波矢k=π/2一定，γ=0.2，跳跃常数J=1，不等幅跳跃分别为α=2和β=3，如图9所示.

图9 单粒子波包的演化示意图（Nc=50、51，N0=90）Fig.9 Evolutionary schematic of the single-particle wave packet（Nc=50、51，N0=90）

图9展示了波包随着时间的演化过程，从格点为N0=90的初始位置开始行进，行进过程中在Nc=50和Nc=51处遇到了散射中心±iγ.此后，波包分裂为反射波和透射波，一部分按原定方向继续前进，另一部分按与入射方向相反的路径返回.值得注意的是，对于一个相反方向入射的单粒子波包，其随时间演化的行进轨迹应该与原定入射方向的波包行进轨迹基本完全相反.

结合上述两个相反方向入射的粒子波包在该系统下的散射行为，提出假设：对于一个反向入射粒子波包散射行为几乎与原入射方向完全相反的系统，存在一种情况使其某一方向的反射几率与相反方向的透射几率均等于0，即rL=tR=0，rR=tL=0.两组关系式中任意一种能够得以验证，均可为实验中制备具有单向输运性即单通性的量子开关元件[13]提供理论基础.为验证这种类似二极管性质的系统是否成立，理论上可以通过调制系统参数加以计算.

2.2 单通性系统的构建

为了找到某一临界点使系统具备单向输运性，将分两种情况进行讨论：

（1）考虑满足公式（19）哈密顿量的非厄米系统.单粒子波包由任意方向入射至一维无限长的紧束缚链上，令系统内α=0，β≠0，rL=tR=0，可得虚数势γ与波矢k的关系为γ=ieik.接下来令波矢k=π/6，根据关系式γ=ieik得到利用数值模拟求得单粒子波包在特定参数下的演化规律，规定系统长度为N=200，跳跃常数J=1，波包宽度ω=1/20，单粒子波包双向入射时的初始位置分别为N0=10和N0=190，演化结果如图10所示.

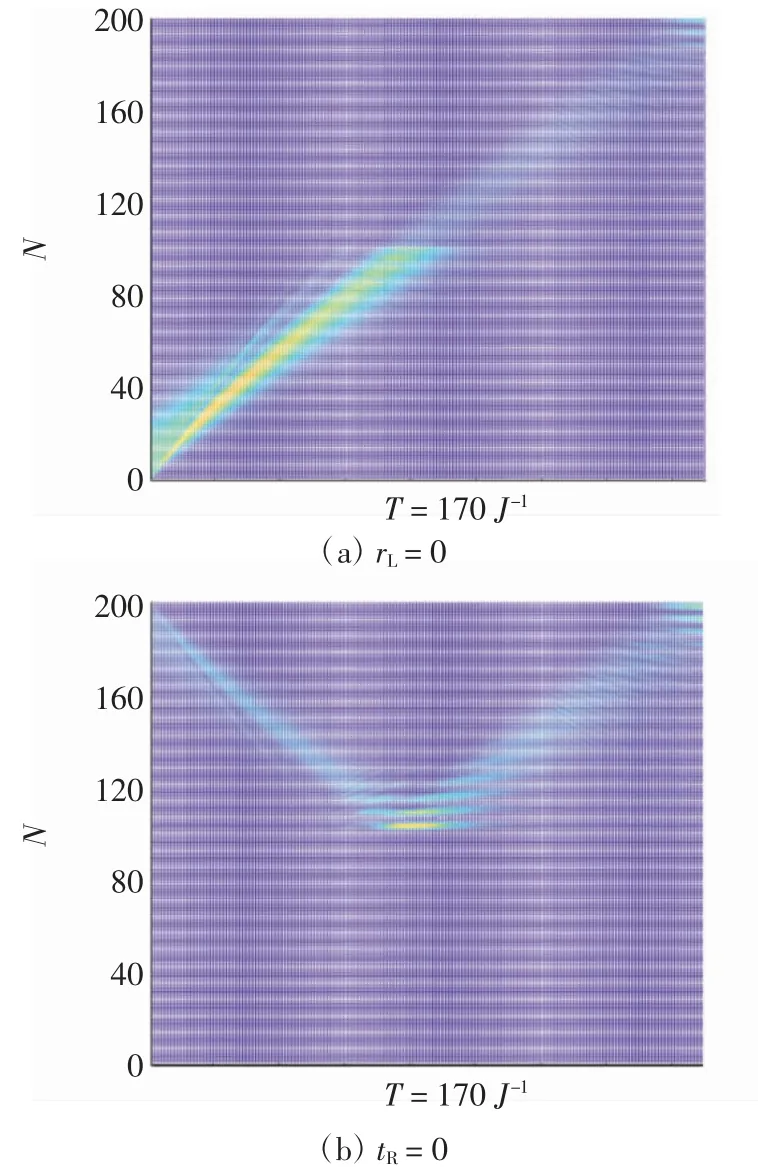
图10 单粒子波包在特定参数下演化的平面示意图（ω=1/20）Fig.10 Plane schematic diagram of the evolution of a singleparticle wave packet under specific parameters（ω=1/20）

（2）继续观察满足公式（19）哈密顿量的非厄米系统.与第一种情况不同的是，单粒子波包由任意方向入射至一维无限长的紧束缚链上，此时令α≠0，β=0，rR=tL=0，可得γ与波矢k的关系为γ=ieik.接下来令波矢k=π/3，根据关系式γ=-ieik得到γ=-i/2+利用数值模拟求得高斯波包在特定参数下的演化规律，规定调整波包宽度为ω=1/5，其余条件不变，演化结果如图11所示.

对比图10和图11可知，两种不同情况下分别设置不等幅跳跃中的某一参数为0，均可以很好地找到满足单向输运性的参数值及关系式.此外，由于非对称耦合散射中心的诱导，单粒子波包发生共振穿透等行为说明了其单向输运性特点的存在.解析与数值模拟的吻合验证了前文提出关于单通性系统存在的假设，说明理论上确实存在这样两个临界点，它们可以有效保证单粒子波包的单向输运性，实验中可以通过调节参数的大小来实现这种装置的制备.

图11 单粒子波包在特定参数下演化的平面示意图（ω=1/5）Fig.11 Plane schematic diagram of the evolution of a singleparticle wave packet under specific parameters（ω=1/5）

对比现有成熟的理论基础，研究人员已经完成了对厄米体系中粒子在化学势作用下动力学行为的基本运算和分析，且可以通过操纵光晶格等系统来完成对量子态的调制.但在非厄米体系中，仅仅研究在位势影响下非厄米哈密顿量作用在一维紧束缚链上所得波包的动力学行为还远远不够.

3 结论

本文主要研究了在非对称耦合散射中心作用下，单粒子波包在一维紧束缚链上的动力学行为，得到以下结论：

（1）对于给定的左向散射增益系统（代表外界一直在输入，如+iγ视为一个增益，-iγ视为一个耗散），可以通过满足公式（2）哈密顿量来计算模拟并观察该系统内单粒子波包的动力学行为.

（2）利用解析及数值模拟的方法，得到一维紧束缚链模型上单粒子波包在非对称耦合散射中心的作用下随时间演化的规律.由模拟结果可知，在虚数势和不等幅跳跃的双作用下，可以找到符合条件的临界参数来制备具有单向输运性即单通性的半导体.

（3）非厄米系统中非对称耦合结构的散射中心可以诱导波包发生共振穿透等行为，使得信息的单向性输运在系统中成为可能，这在量子通信[14]领域有很好的应用价值，如制备具有单通性的半导体装置.

单粒子波包作为量子通信中的信号单元，在传播过程中受到非对称耦合散射中心的影响会发生不同的动力学行为变化，利用人工调制系统参数操纵粒子传播的不同效果可以为人们研究量子固体器件提供理论基础，并为今后信号传输的多样性研究提供便利.