沥青船主尺度要素统计分析
2022-10-15张秋萍金庭宇黄光兵
张秋萍,金庭宇,姚 文,黄光兵
(1.中船澄西船舶修造有限公司,江苏 江阴 214433;2.大连理工大学 船舶工程学院,辽宁 大连 116024)
沥青船是一种特殊运输船,国际海事组织将其定义为2类化学品船。由于运输的沥青温度大多在140 ℃~ 200 ℃之间,最大加热温度为250 ℃,故沥青船是一种高要求、高技术的船舶。
目前对沥青船的总体设计研究,已有吴晓莲和王国强分别分析总结了12 800 t和37 000 t沥青船的总体设计思路和要点[1-2];许军对7 800 t沥青船进行了型线设计等研究[3]。纵观文献,还未见对沥青船主尺度要素统计和回归分析的研究。管官论证了大数据技术在早期船舶设计中对主尺度确定等方面的作用[4],本文据此对搜集的沥青船船型数据进行主尺度特点研究,借助常规回归模型和BP神经网络探究沥青船主尺度要素和其载质量之间的数学关系,并筛选出拟合优度较高的沥青船主尺度估算模型。
1 沥青船设计特点
沥青船作为运输高温液态沥青的特殊危险化学品船,对开发、设计和建造的要求明显区别于传统化学品船和油船,尤其是液态沥青的加热和保温系统要求严苛。虽然沥青航运市场存在独立式和整体式2类液货舱型,但根据停靠港口、航线距离、载货量和建造成本等多方面综合评比,绝大部分沥青船都采用独立液货舱型式设计建造。在设计前期,要综合考虑液货舱结构型式、支撑装置、定位兼防滑移装置、防浮和防翻转装置,而沥青船的完整稳性和破舱稳性也不容忽视。
沥青船型属于载重的容积型船,增加型深(D)或型深吃水比(D/d,d为结构吃水),是提高积载因数或舱容最常用的有效措施。不过,如果浮力偏小且稳性不足,快速性也达不到要求时,就要在考虑容量大小的同时,权衡各方因素,全面合理地调整主尺度,而不是局限于改变型深。载质量对沥青船营运经济性有重要影响,比如同样登记吨位的沥青船,载货量大者经济性要好些。
2 沥青船主尺度回归分析
从国际船级社协会(IACS)官网搜集到168艘沥青船样本,其中5 000 DWT以下的沥青船多集中在2000年以前,2006年以后,沥青船吨位逐渐扩大,5年内建成交付的吨位多在5 000 DWT到7 000 DWT之间,2010年开始出现万吨以上的沥青船。所以考虑到时效性和实际参考价值,本文进行数据分析的样本基本选取2000年以后建成服役的沥青船138艘,然后从中减去主尺度信息不全的和同一系列沥青船中信息完全相同的数据,这样得到具有代表性的沥青船72艘。并以此72艘沥青船的统计数据进行沥青船主尺度要素分析。
样本沥青船的船长(L) 分布在65.0~176.9 m之间;型宽(B) 大致位于10.8~32.2 m范围内;D介于4.5~18.1 m;d基本在4.013~12.617 m;载质量(m)分布在1 043~46 178 t。
2.1 沥青船主尺度比范围
分析沥青船统计数据,可知其船长吃水比(L/d)和长深比(L/D)相对比较大,表1为样本沥青船主尺度比范围。如果已知沥青船某主尺度,可据表1对其他相关主尺度进行粗略估算。

表1 样本沥青船尺度比范围
2.2 正态性分析
回归之前,首先验证搜集的数据是否符合正态分布。沥青船样本的偏度及峰度见表2,其根据统计学理论计算沥青船L、B、D、d和m的偏度、峰度及标准误。可见这些值都在可接受的范围,从而认为沥青船样本数据近似服从正态分布,可进一步研究。
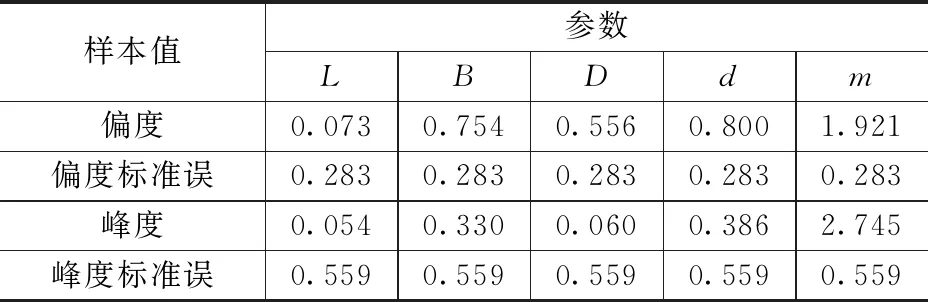
表2 沥青船样本的偏度及峰度
2.3 敏感性分析
为探究沥青船主尺度对载质量的相对重要性,采用相对敏感性分析法[5],定义敏感系数SA来衡量各主尺度变化对载质量变化的影响程度。
选取船体尺度适中、设计建造时间较近、数据来源较权威、可靠性有保证的17 000 DWT沥青船作为参考船型。该船长155 m,型宽23.5 m,型深13.2 m,吃水8.5 m,载质量为17 705.3 t。计算并绘制沥青船主尺度对载质量的敏感性分析如图1所示。图1中,横坐标Δm/m0表示不同沥青船载质量m与参考沥青船载质量m0的差值Δm与m0的比值。以图1(a)为例,纵坐标ΔL/L0代表样本沥青船长L与参考沥青船船长L0的差值ΔL与L0的比值,这样得到的直线斜率就表示L对m的敏感度系数。以此类推,不同沥青船的B、D、d和参考沥青船相应参数的差值分别为ΔB、ΔD、Δd,并依次算得B、D、d对m的敏感性系数,分别见图1 (b)、(c)、(d)。最后得到沥青船各主尺度对载质量的敏感度相对大小,如图1 (e)所示。
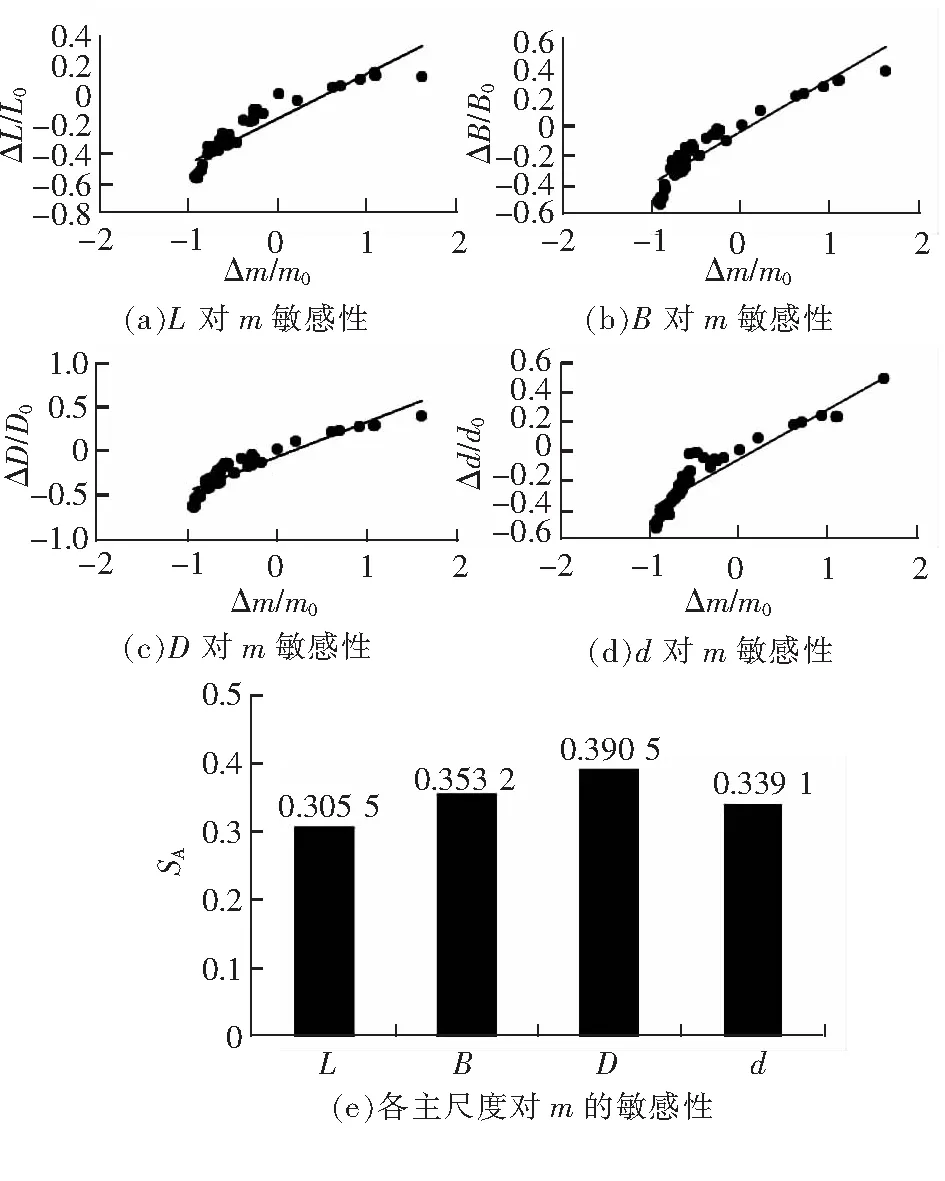
图1 沥青船各主尺度对载质量的敏感性分析
2.4 单变量回归分析
由上述敏感性分析可知,沥青船4个主尺度对其载质量都有一定程度的影响,下面以沥青船m为自变量,以4个主尺度为单变量分别进行数据回归,拟合沥青船主尺度与载质量间的数学表达式。
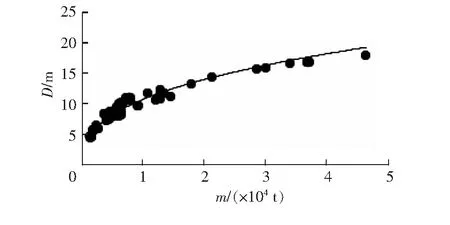
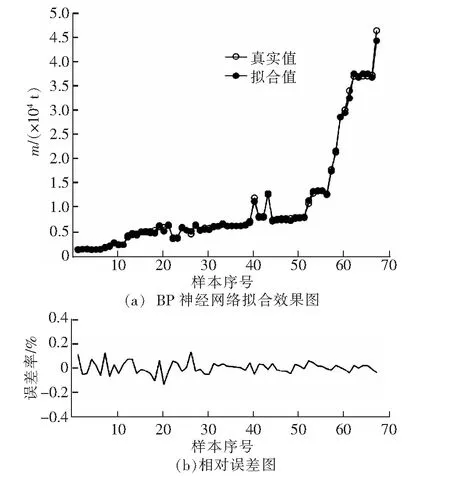
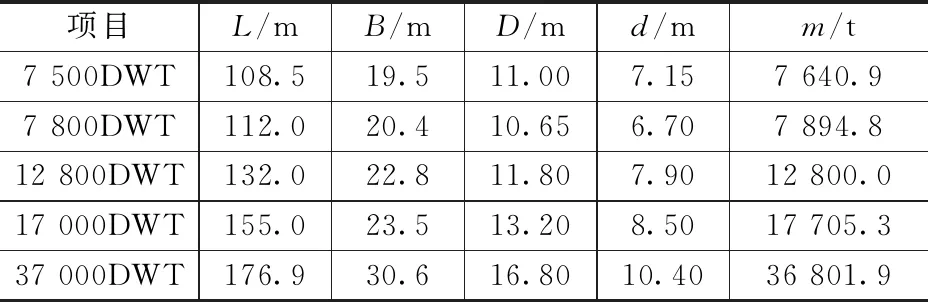
为了保证回归模型有足够的可靠性预测数据,需要依据统计学原理对所得回归表达式进行显著性检验。这里采用无量纲系数R2(R为相关系数)检验显著性。R2的数值越靠近1,拟合度越好;而R2的数值离1越远,表明拟合水平越差。普遍认为,R2>0.9时,拟合度好;0.8 由于需要从72艘沥青船中预留出5艘用于最后回归结果检验,下面以67艘沥青船样本数据来回归分析L、B、D、d和m的关系。 (1)L与m的统计关系。 L-m的散点分布图如图2所示,其回归式见式(1)、式(2): L=8.069 6m0.291 9。 (1) 此时,R2=0.971 2。 L=4.659 3[ln(m)]2-50.155ln(m)+185.9。 (2) 此时,R2=0.972 4。 图2 L - m的散点分布图 (2)B与m的统计关系。 B-m的散点分布如图3所示,其回归式见式(3)、式(4): B=1.382 6m0.294 1。 (3) 此时,R2=0.968 5。 B=0.761 3[ln(m)]2-7.827 7ln(m)+28.388。 (4) 此时,R2=0.974 2。 图3 B-m的散点分布图 (3)D与m的统计关系。 D-m的散点分布如图4所示,其回归式见式(5)、式(6): D=0.342m0.376。 (5) 此时,R2=0.946 7。 D=0.339 1[ln(m)]2-2.400 4ln(m)+ 4.506 6。 (6) 此时,R2=0.961 9。 图4 D-m的散点分布图 (4)d与m的统计关系。 d-m的散点分布如图5所示,其回归式见式(7)、式(8): d=0.547 5m0.282 9。 (7) 此时,R2=0.958 1。 d=0.280 3[ln(m)]2-2.998 4ln(m)+ 11.285。 (8) 此时,R2=0.988 5。 图5 d-m的散点分布图 沥青船方案设计早期,以载质量为自变量的单变量回归模型用于沥青船主尺度初步估算简单有效。随着设计深入,要考虑的因素变多,沥青船载质量与各个主尺度和船型系数之间相互制约,必须综合考虑多个维度的影响,就需要以沥青船多个主尺度为自变量,以载质量作为因变量,进行多元数学模型的构建和拟合,才能得到更加符合实际的结果。 多元线性回归式的一般表示为: y=β0+β1x1+β2x2+…+βnxn+ε, (9) 式中,y为因变量;x1,x2,…,xn为自变量;β0为常数;β1,β2,…,βn为回归系数;ε为随机误差。 由于沥青船船长、型宽、型深和吃水对其载质量的敏感度系数不同,而型深相比于吃水对沥青船载质量的敏感性更大一些。故下面以船长、型宽和型深3个主尺度为自变量对沥青船载质量进行多变量回归。 沥青船载质量的多元回归分别用线性,二次、三次、乘幂和混合模型(指数,对数、开方、-1次幂)进行拟合,按照相关系数高低和回归式简便程度整理,得到了2个变量和3个变量的载质量回归式,如式(10)、式(11)和式(12)所示: m=14 546.466+97.208B2-2 748.188B+ 90.366L。 (10) 此时,R2=0.941。 ln(m)=5.867+0.013L+0.003B+0.141D。 (11) 此时,R2=0.956。 m=0.042 8L1.763B0.826D0.599。 (12) 此时,R2=0.968。 随着人工智能的发展,BP神经网络对各种输入变量和输出变量间的非线性多元模型拟合具有更好的可靠性和更强的适应性。这里采用BP神经网络探究沥青船主尺度与载质量之间的映射关系,将沥青船的船长、型宽和型深3个维度的主尺度作为输入层变量,将载质量的自然对数作为输出层变量,采用3层网络结构[6]对沥青船的统计样本训练和预测,根据神经元经验公式,隐藏层结构的神经元个数在整个训练过程中的取值范围是[3,12]。 在BP神经网络工具箱里对67艘沥青船样本的主尺度与载质量之间的关系进行学习,学习过程中调节各层连接权值,沥青船学习后的拟合效果和相对误差如图6所示。 图6 沥青船学习后的拟合效果和相对误差 从图6 (a)拟合值和真实值之间的纵向距离可知,BP神经网络对67艘沥青船的载质量预测值和实际值接近度较高;从图6 (b)的相对误差图可知,BP神经网络工具箱的拟合模型效果较好,可以利用该BP神经网络模型通过输入主尺度对沥青船的载质量进行评估。 用预留的5艘沥青船验证回归模型的拟合度和准确性,对单变量回归、多元回归和BP神经网络拟合模型分别进行有效性验证。沥青船主尺度见表3。 表3沥青船主尺度 表4为沥青船主尺度要素模型验证结果,由表4可见,沥青船的统计数据回归误差大都在±10%以内,拟合模型整体得到了比较合理的验证。其中,BP神经网络比常规多元拟合的预测误差较小,精度较高。 在沥青船早期船型方案设计时,统计资料法和母型船资料法可以相互补充。本文在大数据下对沥青船主尺度和载质量的回归分析和数学模型拟合并验证,在资料和数据信息有限的情况下,对估算沥青船船型要素提供了一定的参考依据。 表4 沥青船主尺度要素模型验证结果 %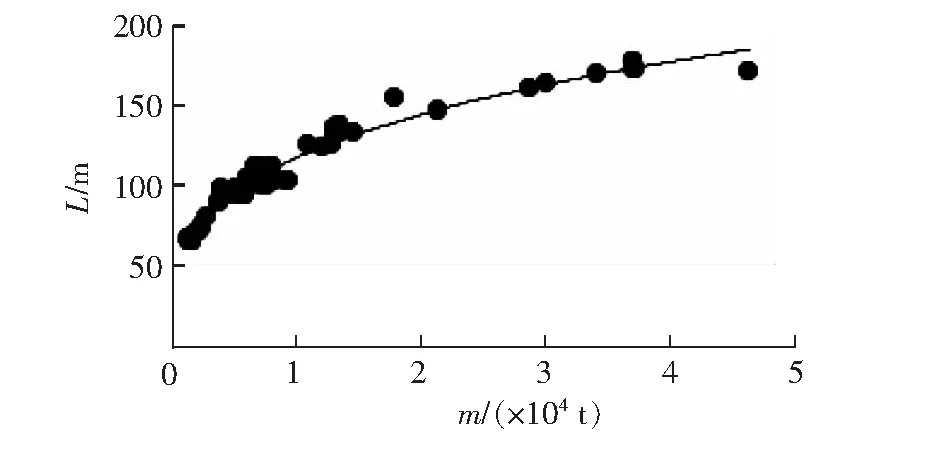


2.5 多元回归分析
2.6 BP 神经网络模型
3 回归模型验证
4 结束语

