基于T-S模糊故障树的船舶轴系故障排除方法研究

张荣国，刘金林，房诗雨，古 铮

(海军工程大学 动力工程学院，湖北 武汉 430033)

轴系是船舶动力装置的重要组成部分之一，其主要任务是连接主机(机组)与推进器，将主机发出的功率传递给推进器，同时又将推进器所产生的推力传给船体，以推动船舶运动[1]。因此轴系的故障排查关系到船舶在海上的航行安全和可靠性。对于轴系的故障诊断，陈小卫等提出利用粗糙集进行主机的故障诊断[2]；汪明等提出基于小波包Shannon 熵与 GA-SVM 的船舶轴系故障诊断方法[3]，周叶等提出基于向量机的轴系故障诊断[4]。上述方法虽然有着较强的理论指导性，但在实施过程中，对人员素质要求过高，故障检测所需设备过多，与故障诊断实践有着较大差距。为有效提高轴系故障诊断效率，降低装置故障检测时间，本文主要立足于船舶轴系故障特点，通过故障机理的分析，构建故障树模型，形成一种简单有效的故障诊断方法，辅助人员进行故障原因排查。

1 T-S模糊故障树理论

1.1 模糊数

T-S模糊故障树在描述基本事件时采用[0，1]区间内模糊数表征其故障程度或故障概率。解决了基本事件故障概率难以获得的问题，并与船员的经验和装置故障实际相结合。本文基本事件的模糊概率μf选择梯形模糊数F表示。梯形隶属度函数示意图见图1。

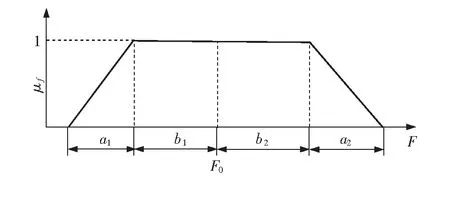
图1 梯形隶属函数示意图

uf=

式中，F0为支撑集中心；a1为左模糊区；b1为左支撑半径；a2为右模糊区；b2为右支撑半径。

1.2 T-S门算法

T-S门是一个万能逼近器[5]，其由一系列if-then规则构成，主要用于描述复杂系统的多态问题[6]。设模糊数(x11,x12,…，x1u1),(x21,x22,…，x2u2)…(xn1,xn2,…，xnun)和(y1,y2,…，yk)分别表示基本事件X=(X1,X2,…，Xn)和上级事件的故障程度，则所对应规则数量m为：

(2)

式中，ui为Xi的故障程度模糊数个数总和。

(3)

可求得其上级事件的模糊概率为：

(4)

(5)

(6)

1.3 T-S模糊故障树重要度分析

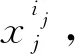
(7)

(8)

式中，t为第j个事件模糊概率不为0的个数。

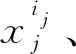
(9)

式中，P(T=Tf)为顶事件在Tf时的模糊概率。

(10)

2 中间轴承T-S模糊故障树建立

中间轴承主要由壳体(轴承盖、轴承座)、甩油盘、注油斗、轴瓦(上轴瓦、下轴瓦)、挡油圈、油封、冷却盘管组件、轴瓦测温用电阻式传感器、油温测量压力式温度计、液位测量用油标尺及与外部接管的配对接头等零部件组成。

2.1 中间轴承T-S故障树构建

将中间轴承的轴瓦高温报警作为顶事件。总结轴瓦故障原因并建立T-S模糊故障树，中间轴承轴瓦高温故障T-S模糊故障树如图2所示。各个事件的编号所对应名称如表1所示。

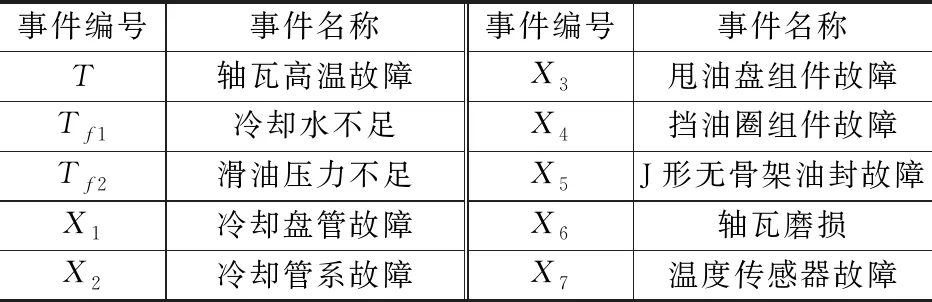
表1 各个事件的编号所对应名称

2.2 T-S模糊故障树门规则构建

根据轴系运行历史故障数据情况以及专家的工作经验，将中间轴承的故障情况分为3种状态，即(0，0.5，1)，分别表示未发生故障状态、中等程度故障状态和严重故障状态，并以此得到各个T-S模糊故障树门的规则如表2、表3、表4所示。

表2 T-S模糊故障树门1规则表

表3 T-S模糊故障树门2规则表

隶属函数的选择，a1=a2=0.1，b1=b2=0.3。以表2中的规则2为例，其含义是：当事件X1及X2的故障程度分别为(0，0.5)时，导致事件Tf1故障程度为(0，0.5，1)的可能性为(0.2，0.5，0.3)。

表4 T-S模糊故障树门3规则表

3 T-S模糊故障树分析

3.1 模糊概率性分析

本文采用专家调查法获取基本事件的模糊概率并采取层次分析法对专家权重进行衡量。层次分析法是一种定量与定性分析相结合的方法，主要适用于评判因素比较少的情况。把复杂问题分解成若干个有联系的有序层次，以直观的形式得出多参数之间的相对权重。根据装备构造熟悉程度、装备运行了解程度及维修熟悉度等几个方面综合考量专家的可信度。根据判别尺度[7]，将专家可信度进行两两相比较，得到相关比较值。由此可得到不同专家在评估过程中所占比重k。专家(r)根据经验以及对中间轴承的运行状态评估基本事件Xj的概率区间[Lrj,Rrj]，得到区间中值为Srj=(Lrj+Rrj)/2，并结合其评估权重kr，则可得到该专家对于此基本事件Xj的模糊概率Prj：

Prj=kr[Lrj,Srj,Rrj]。

(11)

综上所述，求得基本事件Xj的模糊概率Pj为：

(12)

由此可得，基本事件在故障状态为1时的模糊概率如表5所示，并假设每个基本事件在故障状态为1和0.5的模糊概率相等。

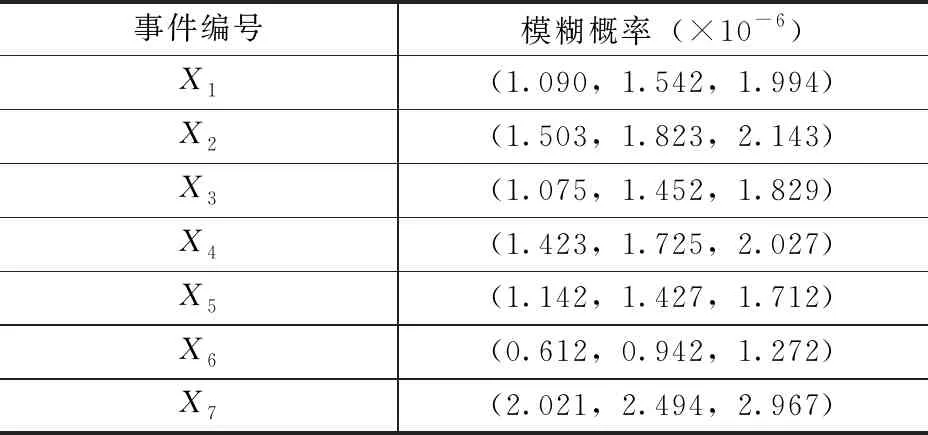
表5 基本事件在故障状态为1时的模糊概率表

通过各个T-S模糊故障树门规则由下到上计算各级中间事件以及顶事件的模糊概率。以表2中T-S模糊故障树门规则为例，由X1和X2的模糊概率联立公式(3)和(4)，可得Tf1在不同故障程度下的模糊概率：

同理可求得Tf2中间事件的模糊概率为：

最后求得顶事件的模糊概率：

由上可知，中间轴承异常过热故障的概率与基本事件的概率仍处于同一数量级，不同之处在于发生严重故障概率高于基本事件，与实际情况比较相符合，验证了该算法的可行性。

3.2 模糊可能性分析

假设在中间轴承异常发热时，各基本事件的故障状态分别是:x1=0.2、x2=0.1、x3=0.2、x4=0.1、x5=0.2、x6=0.2、x7=0.2。以表2中T-S模糊故障树门规则为例，联立式(5)，可求得事件X1和X2的隶属度，T-S模糊故障树门1对应的隶属度如表6所示，μ为某一事件的隶属度。

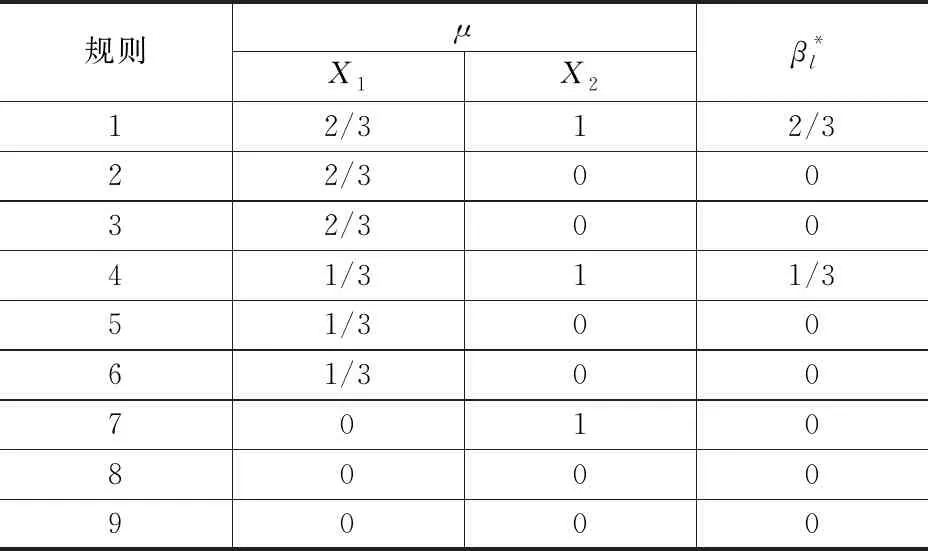
表6 T-S模糊故障树门1对应的隶属度

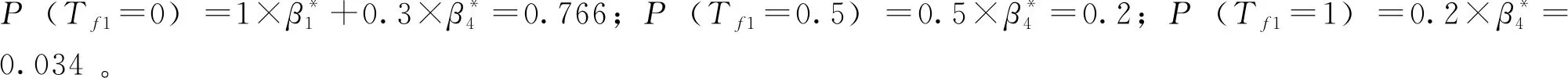
类似推导可求得其余中间事件在不同故障状态下的模糊可能性，并将各中间事件的隶属度用模糊可能性代替，最终可得到顶事件的模糊可能性：

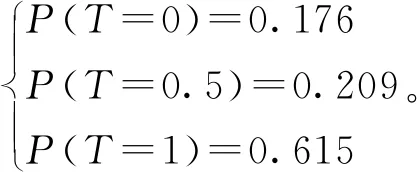
由计算结果可得，当单个基本事件发生细小故障时，对顶事件的故障影响较小，当多个基本事件累加之后，对于顶事件的影响较大。表明计算结果与实际情况相符合，由此应用该方法可以求得顶事件的故障模糊可能性。

3.3 模糊故障树重要度分析

表7 基本事件在不同故障程度下的模糊概率重要度

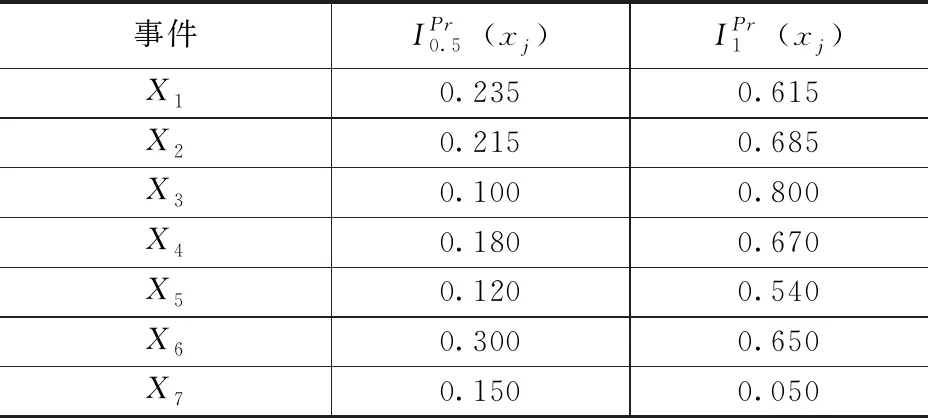
表8 基本事件的模糊概率重要度

由此可计算基本事件的关键重要度。在进行关键重要度计算时，采用基本事件及顶事件的模糊概率中值作为其精确值。以X1为例，计算其在故障状态为0.5时对顶事件的关键重要度，联立公式(9)可得：

同理可得其余基本事件在0.5和1故障状态时，对顶事件的模糊关键重要度。在不同故障程度下，基本事件对顶事件的模糊关键重要度见表9，基本事件的模糊关键重要度见表10。

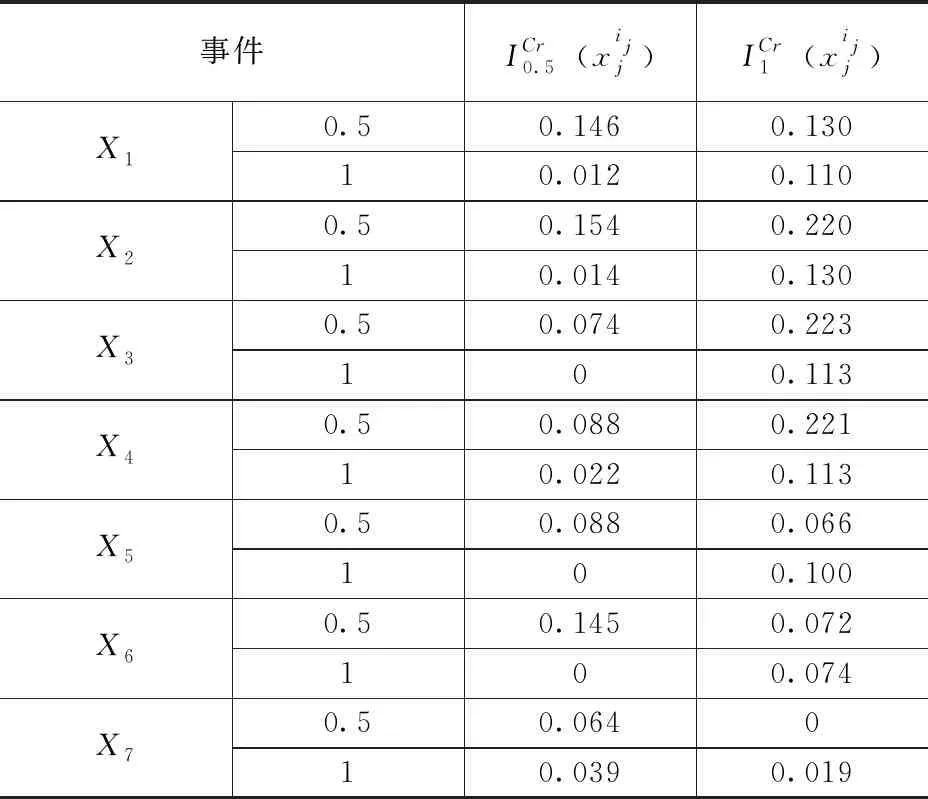
表9 在不同故障程度下，基本事件对顶事件的模糊关键重要度

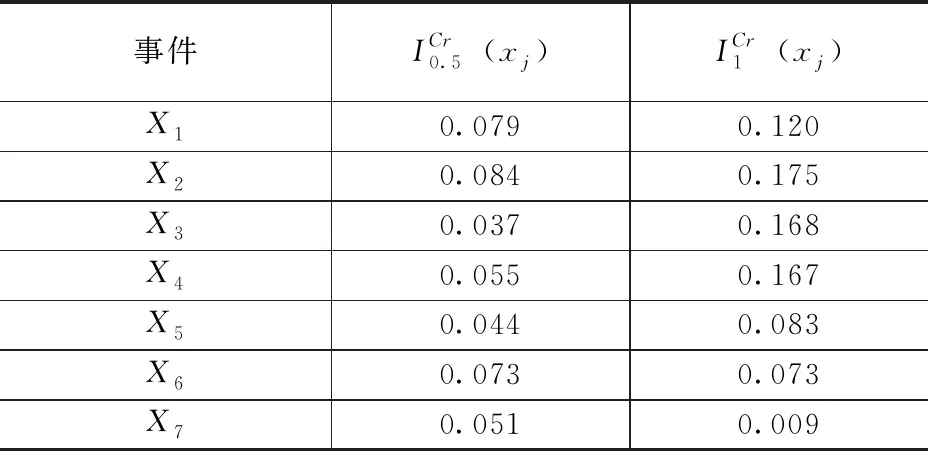
表10 基本事件的模糊关键重要度

当中间轴承发热异常状态为0.5时，各基本事件模糊关键重要度大小排序：

X2>X1>X6>X4>X7>X5>X3。

当中间轴承发热异常状态为1时，各基本事件模糊关键重要度大小排序：

X2>X3>X4>X1>X5>X6>X7。

基于上述分析可知，当轴系中间轴承出现异常发热情况时，可根据上述的排列顺序进行故障排查。研究结果表明，当轴系中间轴承出现发热异常故障时，冷却管系出现故障的可能性较大，符合实际情况，验证了理论研究方法的有效性，能够为轴系故障排除提供理论支撑。

4 结束语

1)针对船舶轴系故障诊断理论与实际应用之间存在较大差距的问题，本文提出了基于T-S模糊故障树的轴系智能故障诊断方法。该方法在传统T-S故障树基础上，融合了模糊数学的有关理论，解决了在轴系突发故障情况下，其基本事件的故障概率难以获得的困难。

2)为能有效反应不同专家之间对轴系故障基本事件故障概率统计时的差异，将层次分析法应用于专家打分法中。根据专家在装备的组成、原理详解及维修熟悉度的不同，通过层次分析法得到其在专家调查法中的权重。由此能更好的反应不同专家对于基本事件的影响程度，使得到的概率更加贴近于实际。

3)综合运用T-S模糊故障树理论与基于层次分析法的专家打分法对船舶轴系中的中间轴承发热异常故障进行故障分析。最终得到基本事件的模糊关键重要度排序，并基于此排序进行故障排查，验证了理论研究的可行性，为轴系故障诊断排除提供了理论依据。