最优尺度回归分析的应用及SPSS软件实现

王瑞平 李斌

（上海市皮肤病医院临床研究与创新转化中心 上海 200443）

临床研究中，研究者完成数据采集和数据录入后，一项重要的工作就是根据其所制定的研究目标开展统计分析。在描述性临床研究设计和临床试验研究的亚组分析中，由于混杂因素和（或）效应修饰因素的作用，研究者在数据分析阶段通常会采用多因素分析方法控制潜在的影响因素，来评估“暴露与结局”和“干预与效应”之间独立关联强度。多因素分析的方法有很多，例如logistic回归、多元线性回归、广义线性模型、广义相加模型、最优尺度回归、Cox回归、二项式分布回归、Poisson回归等，每一种多因素分析方法都有其适用的条件。最优尺度回归分析（optimal scaling）适用于因变量为定量变量，自变量为定量变量或定性变量的情况。其分析过程将定性变量不同取值进行量化处理，从而将定性变量转换为数值型进行统计分析，突破定性变量对分析模型选择的限制，扩大了回归分析的应用能力。本文采用示例的方式，重点介绍最优尺度回归分析的定义、应用条件、SPSS软件实现等内容，以期为研究者今后开展最优尺度回归分析提供参考。

1 最优尺度回归分析的概念

正如本刊2022年第43卷第1期“临床研究规范”专栏《临床医学研究数据分类浅谈》[1]一文中所述，临床研究中的数据通常可以分为两大类，即定量变量和定性变量，定量变量可以进一步细分为连续性变量和离散型变量，而定性变量可以进一步分为二分类变量、多分类有序变量和多分类无序变量。临床研究多因素分析方法的选择即是基于变量类型和特点而进行的。

最优尺度回归分析，也称分类回归（categorical regression），适用于因变量为定量变量，自变量为定量变量或定性变量的情况。对于同样适用于因变量为定量变量的一般线性回归，其模型对数据的要求十分严格，当遇到定性变量时，一般线性回归无法准确地反映定性变量不同取值的距离，比如性别变量，男性和女性本身是平级的，没有大小、顺序、趋势区分，若直接纳入线性回归模型，则可能会失去自身的意义。而最优尺度回归分析便可突破定性变量对分析模型选择的限制，将定性变量不同取值进行量化处理，转换为数值型进行统计分析，扩大回归分析的应用能力。

2 最优尺度回归分析的应用条件

如前所示，临床研究中的数据一般分为定量变量和定性变量两大类，而数据分析方法的选择均是基于不同的变量类型来开展。如图1所示，根据多因素分析模型中因变量和自变量的不同分类组合，可以选择不同的多因素分析模型。当因变量为定性变量时，自变量为定量变量、定性变量、或定量变量和定性变量组合的情况，都可以选择logistic回归分析；当因变量为定量变量，自变量为定量变量时，一般将因变量的定量变量转换为定性变量，然后选择logistic回归分析；当因变量为定量变量，自变量也为定量变量时，一般选择线性回归分析；当因变量为定量变量，自变量为定量变量和定性变量组合时，可以采用广义线性模型或最优尺度回归分析；而当因变量为时间变量（生存年数、随访时间等），自变量为定量变量或定性变量组合时，应选择Cox回归分析。综上，最优尺度回归分析的应用条件为因变量为定量变量，自变量为定量变量或定性变量的情况。

图1 变量分类与多因素分析模型选择参照图

3 最优尺度回归分析在SPSS软件中的实现

为便于理解，本文以“婴儿低出生体质量的孕期潜在危险因素分析”数据库[2]为基础，介绍最优尺度回归分析在SPSS软件实现的操作步骤。如图2所示，数据库中共有9个变量，包括出生体质量（birthweight）、婴儿性别（gender）、母亲年龄（age_m）、妊娠期糖尿病史（disease_inpreg）、孕前 BMI指数（bmi_m）、孕期二手烟烟草暴露（secsmoke_d_preg）、孕期一手烟烟草暴露（fsmoke_d_preg）、分娩孕周（birth_week），以及根据出生体质量是否＜2 500 g判定的低出生体质量情况（blweight）。根据研究目标，确定本研究中出生体质量为因变量，而婴儿性别、母亲年龄、孕期妊娠期糖尿病史、孕前BMI指数、孕期二手烟烟草暴露、孕期一手烟烟草暴露和分娩孕周为自变量。根据前面的分析，如果将“出生体质量”转化为“低出生体质量发生情况（是/否）”，即将其转化为定性变量，后面的分析可选择logistic回归；而如果将出生体质量这个定量变量直接作为因变量，后续的分析选择最优尺度回归分析更为合适。

图2 婴儿低出生体质量的孕期潜在危险因素分析数据库

与其他类型的多因素分析一样，最优尺度回归分析前须通过单因素分析对自变量进行筛选，将单因素分析中“P≤0.05”及“0.05＜P≈0.05”的变量挑选出来，然后作为自变量纳入最优尺度回归模型进行分析。如图3所示，对于“婴儿性别”“妊娠期糖尿病史”和“孕期烟草暴露（一手、二手）”这些分类变量，可以根据“出生体质量”是否符合正态分布，选择t检验或非参数秩和检验进行单因素分析，最终选出“婴儿性别”“妊娠期糖尿病史”“孕期一手烟烟草暴露”和“孕期二手烟烟草暴露”进入最优尺度回归模型。对于“母亲年龄”“孕前BMI指数”和“分娩孕周”此类定量变量，可以通过相关分析和简单线性回归模型来分析变量与“出生体质量”之间的关系，最终选定“分娩孕周”进入最优尺度回归模型。

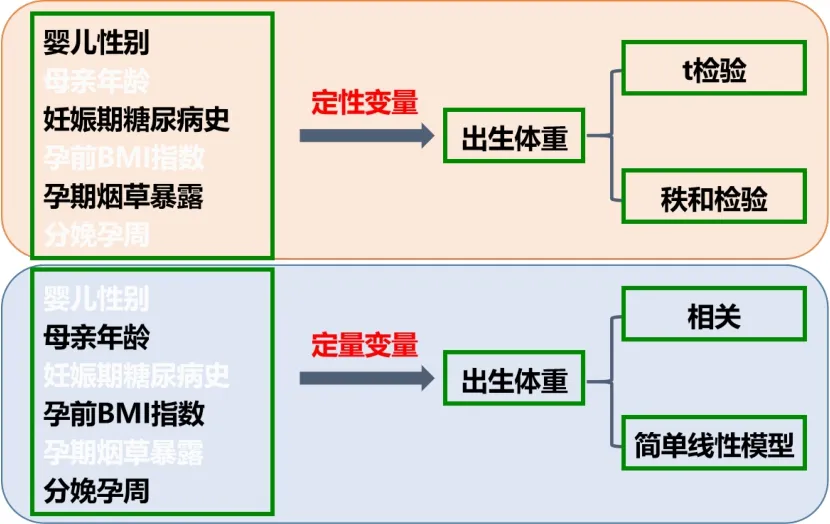
图3 通过单因素分析筛选进入多因素分析的自变量

如图4所示，选择“Analyze（分析）菜单→Regression（回归）次级菜单→Optimal Scaling”，打开对话框，在“Dependent Variable”放入因变量，在“Independent Variables”放入自变量；然后分别点击因变量和每一个自变量，用“Define Scale（定义尺度）”，依据定量变量（nuneric）、定性变量（nominal）、等级变量（ordinal）原则对每一个变量进行调整，完成后再分别点击“output（输出）”和“save（保存）”，打开新的对话框。

图4 最优尺度回归分析过程示意图

如图5所示，在“output”对话框中，勾选“Coefficients（系数）”“Iteration history（迭代过程）”和“ANOVA（方差分析）”，点击“continue”；随后在“save”对话框勾选“save transformed variables to the active dataset（将已转换的变量保存到打开状态下的数据集）”，点击“continue→ok”，输出结果如图6。

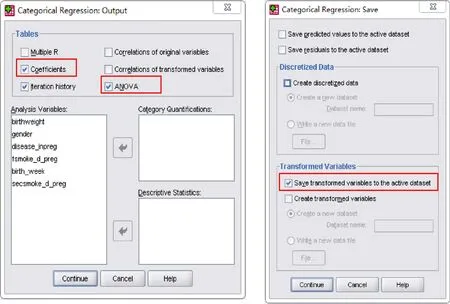
图5 最优尺度回归分析中“Output”和“Save”的设置

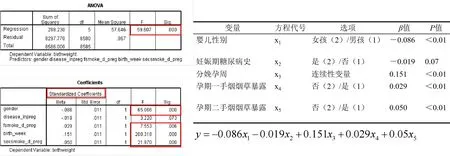
图6 最优尺度回归分析输出的结果及方程

根据ANOVA分析结果，可见模型拟合情况良好（F＝59.61，P＜0.01）；Coefficients结果中，可以看到纳入最优尺度回归分析模型的5个自变量的回归系数β值，及变量的统计分析情况。依据每个自变量的β值，最后写出本研究的最优尺度回归方程为，据此可以分析每一个自变量对因变量（出生体质量）的影响。