基于分层强化学习的电动汽车充电引导方法

2022-10-15江昌旭苏庆列

电力自动化设备 2022年10期

詹华，江昌旭，苏庆列

（1. 福建船政交通职业学院汽车学院，福建福州 350007；2. 福州大学电气工程与自动化学院，福建福州 350108）

0 引言

近年来，在全球能源紧缺和环境恶化的背景下，电动汽车由于其节能、环保等优势在国内外得到了广泛推广［1］。随着越来越多的电动汽车涌入，原有的充电站规模很有可能无法满足其充电需求，由此可能会出现严重的充电排队的现象，这不仅浪费驾驶人员单位时间产出率，而且严重时可能影响配电网电能质量。如何制定有效的电动汽车充电引导策略（包括电动汽车充电目的地策略和充电路径策略）以降低电动汽车总充电费用，是未来电动汽车大规模普及的基础和保障［2-3］。

目前，国内外学者对电动汽车充电引导问题进行了广泛研究。文献［4-5］通过排队论模型建立充电服务定价模型和采用电力系统节点边际电价最优模型对电动汽车充电电价进行优化，以引导电动汽车前往电价较低的充电站进行充电，实现电动汽车总成本最小化。文献［6］结合最短路径算法和排队论M／G／k 模型，提出了一种考虑下一目的地导向下的电动汽车充电引导模型，并采用粒子群优化算法进行求解。文献［7］提出了一种考虑交通和电网状态的电动汽车快速充电引导系统，采用三相最优潮流计算充电站最大可用充电功率，然后电动汽车终端以充电总时间最小为目标对充电引导策略进行优化。然而，以上大部分文献在构建电动汽车充电引导优化模型时进行了大量假设，同时没有考虑到各种不确定性因素对充电引导策略的影响。

实际上，电动汽车充电行为涉及交通、充电站等多个主体，包含了大量的不确定性因素，如交通路况的不确定性、充电站排队时间的不确定性等，造成了电动汽车充电行为具有较强的不确定性。为了更好地处理这些随机变量，有学者采用强化学习RL（Reinforcement Learning）方法解决电动汽车充电引导问题。该方法属于一种免模型算法，其通过与环境不断交互形成一种从状态到动作的映射，以最大化长期累积回报。由于表格型强化学习缺乏有效的机制对高维状态进行描述，基于神经网络的深度强化学习DRL（Deep Reinforcement Learning）算法具有较好的泛化性能，能够以端到端的方式接近全局最优解，被广泛应用于各个领域［8-10］，如围棋、自动控制［11-12］、自动驾驶［13］等。文献［14-15］在考虑充电时间、充电需求、可再生能源间歇性和批发市场电价不确定环境下，采用概率模型和免模型的线性强化学习方法对电动汽车充电电价进行优化，以此引导电动汽车充电。文献［16-17］提出了一种基于深度Q网络强化学习DQN（Deep Q Network）的电动汽车充电引导方法，旨在寻找最优充电路径或充电目的地以最大限度地减少电动汽车的充电总成本。文献［18］提出一种双层充电服务定价模型以实现电动汽车充电引导，提出的模型考虑了起讫点交通需求的不确定性，采用基于梯度和无梯度的深度强化学习解决双层随机优化问题。然而，以上大部分文献在制定电动汽车充电引导策略时要么仅对电动汽车充电目的地进行优化，并采用最短路径算法（如Dijkstra［19］、Floyd算法）生成充电路径；要么在充电目的已知前提下对充电路径进行优化；没有同时考虑到电动汽车充电目的地优化以及充电路径规划，导致优化得到的结果可能并不是最优的策略，从而影响最终的寻优效果。

针对以上问题，本文提出了一种基于分层增强深度Q 网络强化学习HEDQN（Hierarchical Enhanced Deep Q Network）的电动汽车充电引导方法，以制定最优的电动汽车充电引导策略，实现最小化电动汽车充电总费用。所提出的HEDQN 方法采用基于Huber损失函数的双竞争型深度Q网络算法，并包含2 层增强深度Q 网络eDQN（enhanced DQN）算法，分别对电动汽车充电引导目的地和充电路径进行优化决策，以此通过目标的分解来实现更高的求解效率和得到更优的充电引导策略方案。最后，采用某城市实际的交通网络数据进行算例分析，并与现有的其他方法结果进行对比，以验证所提方法的有效性和适应性。

1 电动汽车充电引导数学模型

电动汽车充电引导行为涉及交通、电力、充电站、电动汽车等多个主体，包含了大量的不确定性因素，如电动汽车初始荷电状态SOC（State Of Charge）的不确定性、交通路况的不确定性、充电排队时间的不确定性等，这些不确定因素造成电动汽车充电行为具有较强的不确定性。当电动汽车需要进行充电时，电动汽车用户首先根据当前车辆状况、交通系统和充电站状态选定某个目标充电站进行充电，然后在此基础上确定一条最优的行驶路线，使得电动汽车尽快到达充电目的地，同时期望充电的花费尽可能小。因此，可以将以上电动汽车充电引导问题构建为双层随机优化模型，其数学模型为：

以上数学模型包含了电动汽车充电决策时的剩余电量、行驶速度、充电等待时间等多重随机变量。因此，式（1）—（9）构建的模型为双层随机优化模型。上层模型（式（1））为充电引导目的地优化模型，即最小化电动汽车充电费用和前往充电站的旅途费用，其目的是在考虑电动汽车初始SOC、电动汽车行驶速度和电动汽车充电等待时间多重不确定因素下决策出最优的充电目的地，以降低电动汽车总充电费用；下层模型（式（2））为电动汽车充电路径优化模型，其目的是在充电目的地确定的情况下，电动汽车用户根据当前车辆的状态和交通系统状况选择最优的充电路径前往充电目的地，以降低电动汽车旅途费用；式（3）表示电动汽车充电费用，由在充电站k充电的电量费用（见式（4））和充电等待时间的费用组成；式（5）表示电动汽车剩余电量变化情况；式（6）表示电动汽车旅途费用，由在道路l上消耗电量的费用（见式（7））和通过道路l所需要的时间费用（见式（8））组成。

2 基于分层强化学习的电动汽车充电引导系统

本文涉及的电动汽车充电引导策略不仅包括电动汽车充电目的地策略，还包括前往充电目的地的充电路径策略，并且这些动作决策变量都是离散型的。为了更加准确、高效地求解以上双层随机优化问题，本文提出了一种基于分层强化学习的电动汽车充电引导策略方法。

2.1 马尔可夫决策过程

本文构建的电动汽车充电引导模型实际上是一个双层随机优化模型，为了更好地利用分层强化学习方法进行求解，首先需要将该问题转换为一个未知转移概率的马尔可夫决策过程MDP（Markov De-

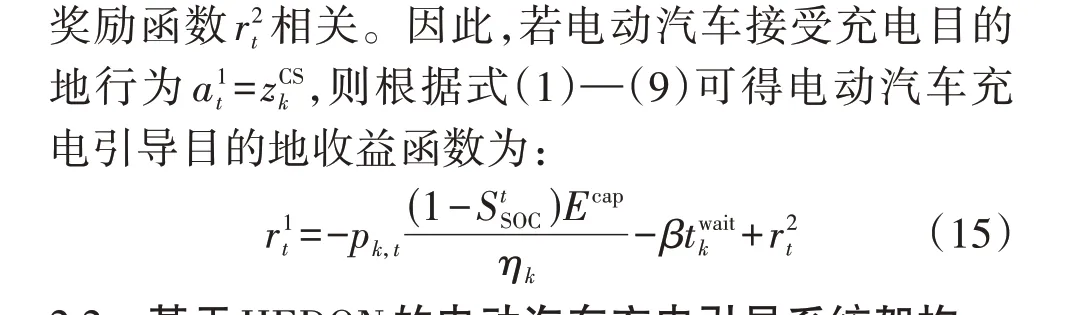
2.2 基于HEDQN的电动汽车充电引导系统架构

2.2.1 HEDQN算法基本架构

2.2.2 基于HEDQN的电动汽车充电引导方法

本文涉及的电动汽车充电引导问题可以分为充电目的地和充电路径双层随机优化问题。不同的任务涉及的主体和目标都不一样，若采用传统单层强化学习，则其状态、行为空间将急剧增加，不仅会影响到强化学习的效率，还会对最优策略的获取造成影响。此外，考虑多种不确定性因素的双层随机优化决策问题本身比较适合使用分层强化学习进行解决。因此，本文提出了HEDQN 算法对电动汽车的充电目的地和充电路径进行决策，以此获得电动汽车充电引导策略，从而达到降低充电费用和旅途费用目的。下层eDQN 的目标为最大化其内部收益，即：

式中：s′和a′分别为下一状态及其动作行为；yt表示使用目标网络得到目标Q值；θ～为目标网络的参数，每经过一定的迭代次数，该值根据当前网络的参数θt进行更新。

本文eDQN 算法主要对式（18）—（21）进行了以下三方面的改进。

1）eDQN改进策略1：深度双Q网络。

传统DQN 算法在计算目标网络Q值时使用式（21），每次都选取下一个状态中最大的Q值所对应的动作，即选择和评估动作都是基于目标网络的参数θ～，这会引起强化学习算法在学习过程中出现过高估计Q值的问题。对此，本文采用深度双Q 网络［8］中的策略，即采用当前网络θt来选择下一状态的最优动作，然后用目标网络θ～来评估动作的Q值，即充分利用DQN的2个神经网络将动作选择和策略评估分离开，以降低过高估计Q值的风险。因此，在计算损失函数时，目标网络Q值式（21）可以修改为：

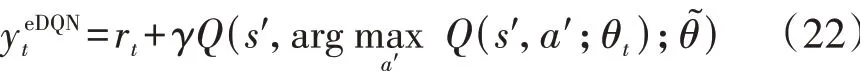
2）eDQN改进策略2：竞争DQN。

原DQN 中，深度神经网络提取的特性直接通过输出层输出相应动作的Q值。为了更准确地评估在某一状态和行为下的Q值，同时加快收敛速度，本文采用竞争DQN［9］对状态和动作进行分层学习。该策略将经过深度神经网络提取的特征分流到全连接层中的2 条支路中：一条支路表示标量状态值函数V（s），另外一条支路表示在状态s下的动作优势值函数A（s，a）。

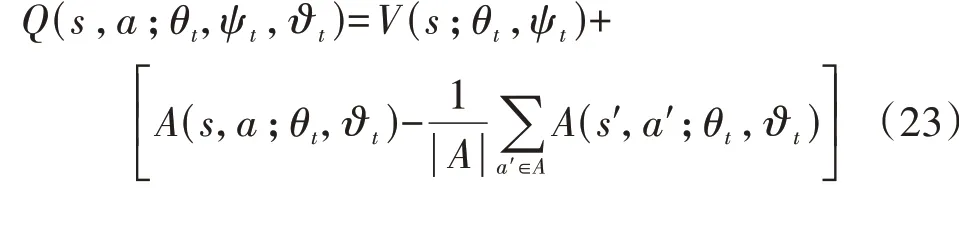
式中：ψt为V(s)所在支路的神经网络参数；ϑt为A（s，a）所在支路的神经网络参数。

3）eDQN改进策略3：Huber损失函数。

尽管MSE 构造的损失函数随着误差的减少，其梯度呈线性递减，该性质有利于算法收敛，但是当误差大于1 时，误差平方将会急剧增大，从而使得模型偏向于惩罚误差较大的点，即将赋予离群点更高的权重，导致牺牲其他正常点的预测效果，从而使模型的整体性能下降。在平均绝对误差MAE（Mean Absolute Error）大于1 时，其惩罚力度保持不变，但是在误差等于0 点处不可导，从而导致求解比较困难。同时，MAE 的梯度恒为1，即使对较小的损失值其梯度也不变，因此不利于算法的学习和收敛。为了改善这种状况，本文采用结合MSE和MAE 两者优势的Huber 损失函数，它能够减少离群点敏感度，同时实现处处可导，该损失函数为：

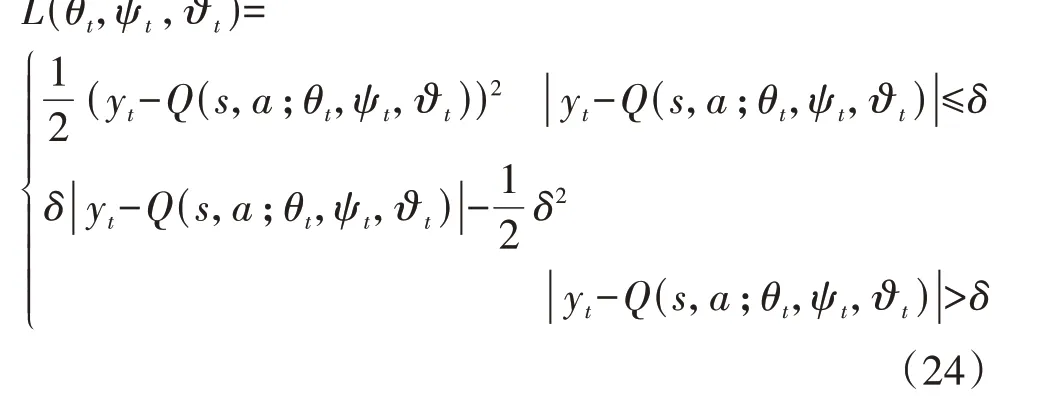
式中：δ为Huber损失函数参数，该值决定了Huber损失函数对MSE和MAE的偏重程度。

2.3 算法流程

3 案例分析

3.1 环境及参数设置

本文选取某市交通地图，其包含39 个节点、67条线路和3 座电动汽车快充电站，如附录B 图B1 所示。根据市政部门城市道路规划以及交通部门车辆监测可以得到各线路的平均行驶速度。电动汽车行驶时，假设其速度服从截断正态分布，其最大值为对应路段的最大行驶速度［16］。

电动汽车电池容量为64 kW·h，每千米耗电量α为0.21 kW·h／km。由于5 号和32 号充电站离中心区位置稍远，该充电站的电价参考某市公布的峰谷平电价分时电价，如表1所示。同时，由于22号充电站靠近中心区，其车流量较大，为了降低大量电动汽车同时涌入22 号充电站进行充电进一步增加充电等待时间概率，将22 号充电站的电价在传统峰谷平分时电价基础上增加0.3元／（kW·h）。由于本文主要的关注点在于电动汽车用户如何根据当前观测状态作出最优充电目的地和充电路径决策，因此本文借鉴文献［3，16］将5号和32号充电站的充电等待时间设置为正态分布。同时，由于22 号充电站靠近中心区，其车流量较大，充电等待时间也长于5号和32号充电站，因此在原有的充电等待时间分布基础上其均值增加20 min。另外，根据全国平均工资，可以得到单位时间价值为8.790 3 元／h［20］。本文设置充电次数M=3，仿真开始时电动汽车随机分布在地图节点上，假设初始SOC 服从均匀分布U(0.4，0.6)。此外，HEDQN 的参数设置如附录B 表B1 所示［10，12］。值得注意的是，这些参数仅在初始化时进行设置，之后不会随着环境的变化而改变。

表1 电动汽车充电站电价和充电等待时间分布Table 1 EV charging price and distribution of charging waiting time

3.2 学习速率α参数确定

深度强化学习算法涉及较多超参数，如学习速率α、折扣因子γ、批大小等。其中，本研究中的α对HEDQN 效果有较大的影响。α越大，权重更新的幅度越大。若α过大，则有可能在梯度下降过程中直接跳过最低点，导致网络收敛到局部最优点，甚至有可能使训练变得发散。为了能够有效确定HEDQN算法的最优学习速率，本文在不同的α下分别对电动汽车充电引导奖励函数、HEDQN 损失函数值和电动汽车充电引导各项指标进行比较分析。

不同α下基于HEDQN 算法的电动汽车充电引导性能比较如图1 所示。从图1（a）可以得出，在训练前1500轮迭代，即在训练开始阶段电动汽车充电引导奖励函数值经历了较大的波动，且其奖励函数远低于收敛时的平均值。这主要有2 个原因：一是由于在开始阶段充电路径和充电目的地决策采用随机搜索，以快速地进行不同充电路径和充电目的地的尝试，以便找到较优的充电引导策略；二是由于在训练前期处于探索阶段，神经网络的权重参数并未达到最优，导致其得到的策略有较大的波动。当α=10-2时，由于学习速率设置过大，其在经过30 000 轮迭代后算法逐渐开始发散；当α=10-3或10-4时，同样由于学习速率设置过大，导致算法在经过1500轮迭代后，电动汽车充电引导奖励函数从-94 逐渐下降到-104，最终收敛到一个局部最优点，如图1（a）所示；当α=10-5时，经过6 000 轮迭代后强化学习算法的奖励函数快速收敛，其奖励函数值基本趋于平稳，此时其损失函数值波动范围也较小，见图1（b）、（c）。

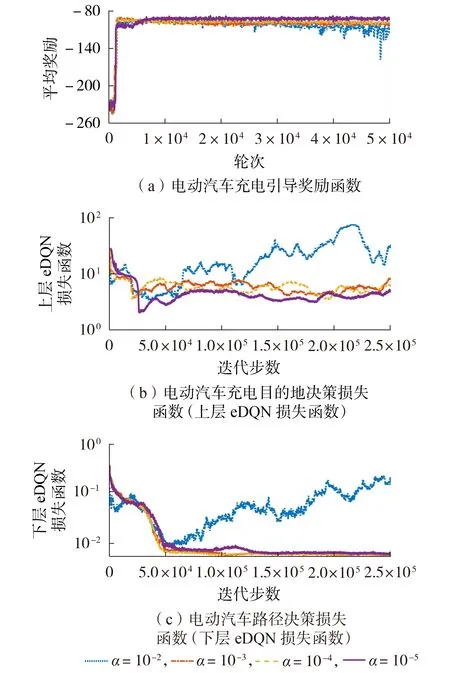
图1 不同学习速率下基于HEDQN算法的电动汽车充电引导性能比较Fig.1 Performance comparison of EV charging navigation based on HEDQN algorithm under different learning rates

为了更加直观地比较不同α对电动汽车充电引导策略的影响，表2 给出了电动汽车充电引导各项指标。从表中可知，当α=10-5时，最终的单次充电平均费用最低，为31.77 元。因此，本文的学习速率最终确定为α=10-5。

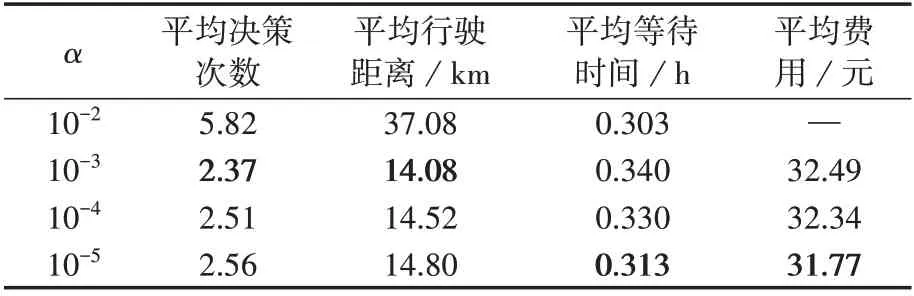
表2 不同学习速率下电动汽车充电引导各指标对比Table 2 Comparison of various indicators of EV charging navigation under different learning rates

3.3 电动汽车决策性能分析

1）同一充电站中电动汽车决策地点统计结果对比分析。

为了验证所提基于HEDQN 的电动汽车充电引导方法的有效性，本文对最后1000轮迭代的结果与基于Dijkstra 最短路径的就近推荐DIS（DIStance）算法的结果进行比较和分析。图2 展示了基于就近推荐DIS 算法和基于HEDQN 的电动汽车充电引导方法对5 号充电站中电动汽车在不同地点决策比例的统计结果（为了节省篇幅，选择5 号充电站进行详细分析）。从图2中可知，当采用就近推荐DIS算法时，电动汽车选择5 号充电站的地点绝大部分位于地图的左上方（如附录B 图B1 所示），即位于5 号充电站附近。另外，由于11、12号节点距离5号充电站的路程相比22 号充电站更远，因此基于就近推荐DIS 算法会直接选择22 号充电站进行充电。相比于就近推荐DIS 算法，基于HEDQN 的电动汽车充电引导方法选择5 号充电站进行充电的地点更多，其新增了11、12、16、19、20 等多个地点。尽管这些位置相比其他充电站位置更远，所需的旅途费用（充电路上消耗的电量费用和时间费用之和）也会略微增加，但是决策时刻其总的充电费用（充电时电费和充电等待时间费用之和）会更低。例如，当电动汽车在11 号节点采用就近推荐DIS算法前往22号充电站充电时其平均旅途费用仅为7.433元，单次平均充电费用为48.932元，而采用基于HEDQN 的电动汽车充电引导方法其前往5 号充电站平均旅途费用9.756 元，但是单次平均充电费用仅需37.142元，减少了24.09%。

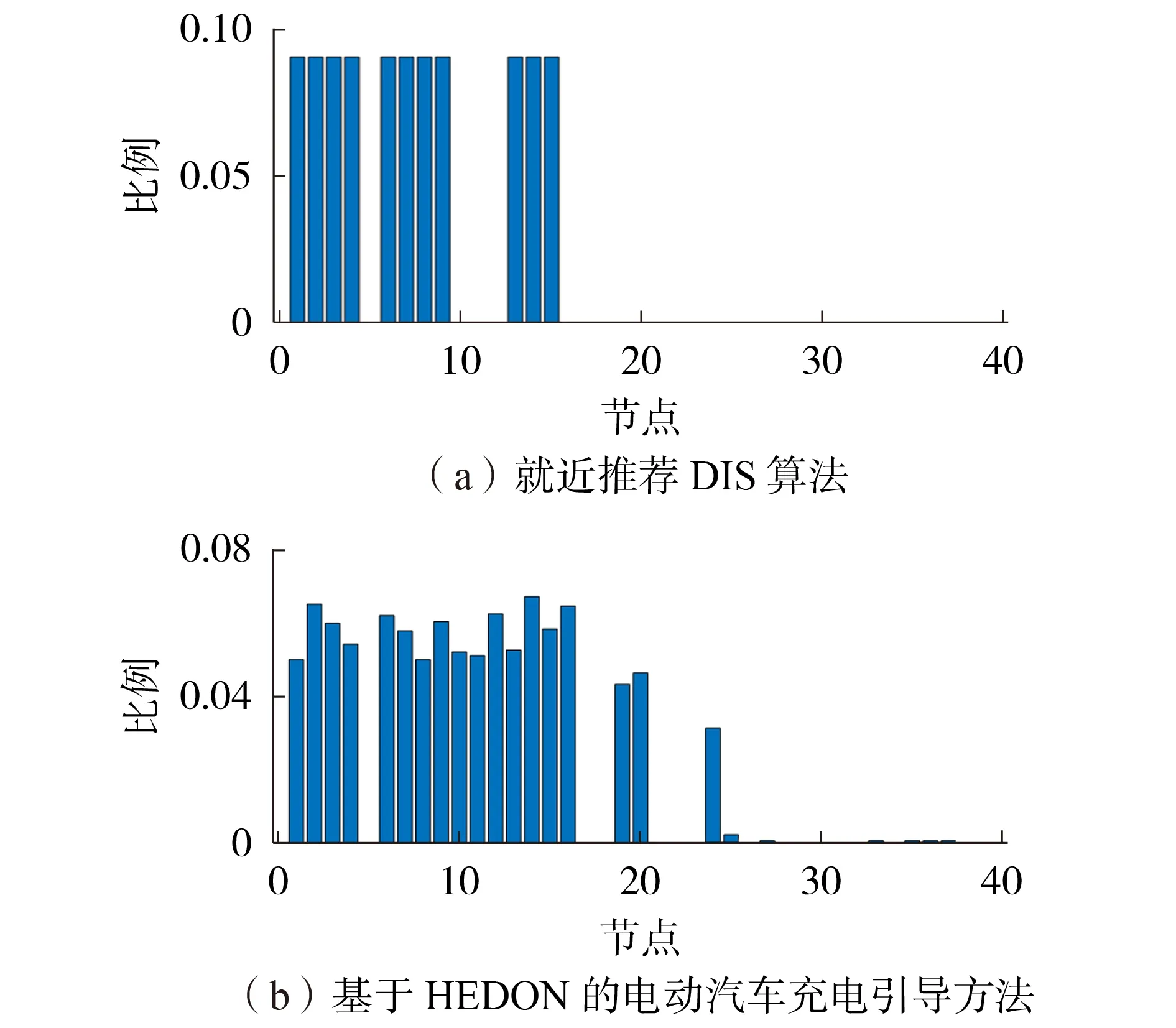
图2 不同算法下5号充电站中电动汽车在不同地点决策比例分析Fig.2 Ratio of EV charging decision in different locations at charging station No.5 under different algorithms

2）电动汽车在不同位置选择各充电目的地比例。

电动汽车在不同地点时选择各充电站的比例如附录B 图B2 所示。从图中可知，电动汽车在绝大多数节点上其充电策略保持不变，这些节点大部分都距离某个充电站位置较近或处于外环上面。如：4、6、7号节点和23号节点分别距离5号充电站和22号充电站距离最近，其选择5 号和22 号充电站的概率接近于1。电动汽车在其他节点上需要根据当前的状态，比如充电时刻、充电决策时的剩余电量、充电电价、等待时间等情况进行进一步决策，以最小化充电的总费用（包括旅途费用和充电费用）。如：当电动汽车的充电决策时间接近高峰电价时（如18:30），电动汽车位于29 号和30 号节点时，其距离22 号充电站较近，为了避免去更远的32 号充电站充电而导致电动汽车在高峰电价时充电，此时HEDQN 算法将给出在22 号充电站进行充电的策略，以减少旅途费用（包括旅途的电量费用和时间费用）。在其他时间点，电动汽车将尽量避开22 号充电站进行充电，因为该充电站的电价较高，并且等待时间较长。

3）不同算法下电动汽车充电引导各项指标比较。

本文将所提出的基于HEDQN 的电动汽车充电引导方法与就近推荐DIS算法［19］、单层DQN算法［16-17］和传统的分层深度Q 网络hDQN（hierarchical Deep Q Network）算法［10］在电动汽车充电引导各项指标进行比较，以进一步验证电动汽车充电引导在充电路径和充电目的地上决策的有效性和正确性。

图3 为不同算法下电动汽车充电引导奖励函数曲线。从图中可知，3 种强化学习算法都能快速地通过调整神经网络权重对电动汽车充电引导策略进行学习，在经历过短暂的学习后达到收敛状态。相比于单层DQN 算法和传统hDQN 算法，所提HEDQN算法通过对Q值估计、神经网络结构和损失函数改进能够有效地提升算法的搜索效率，能够获得更高的奖励函数，从而得到更优的充电引导策略。

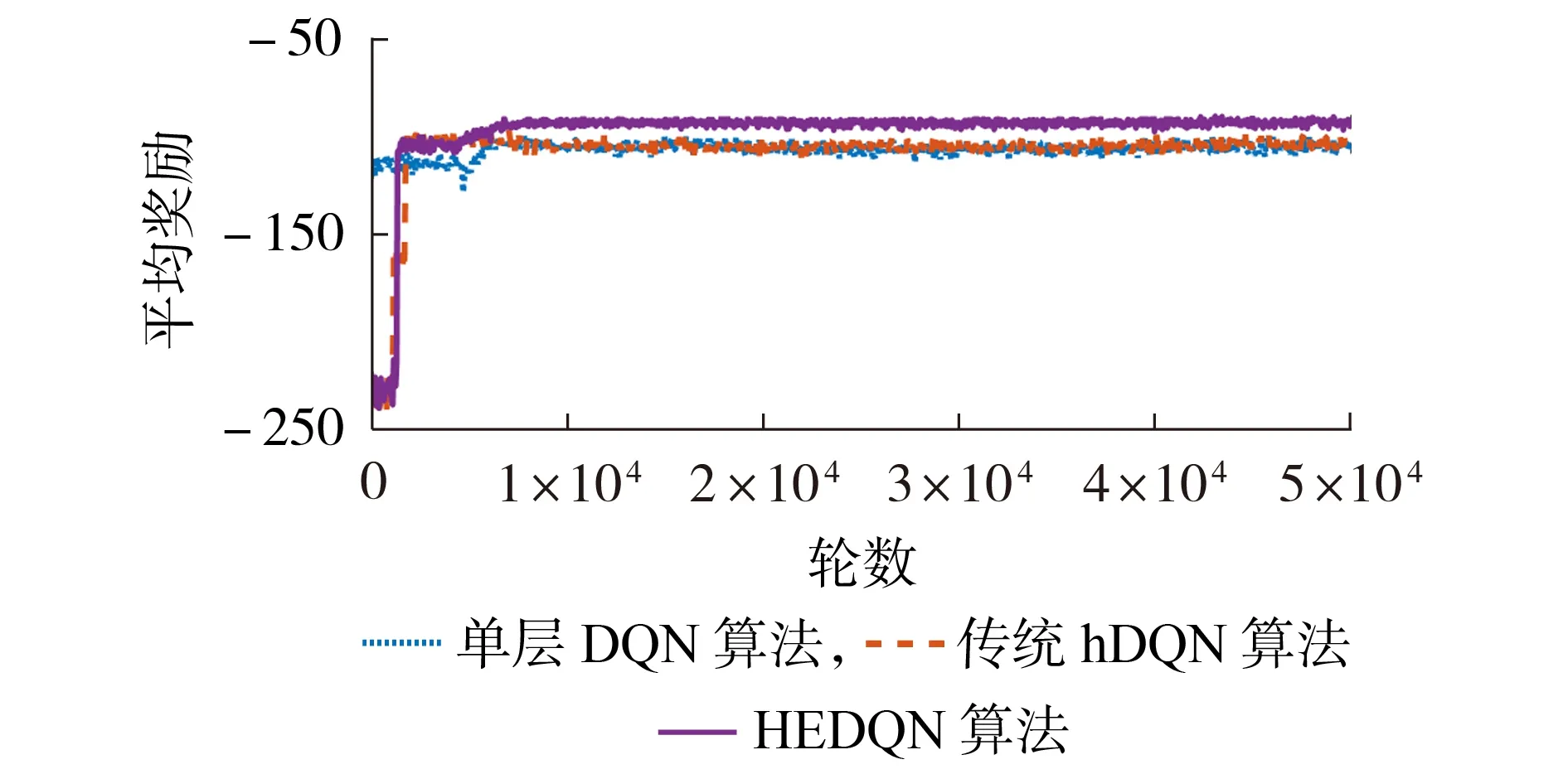
图3 不同算法下电动汽车充电引导奖励函数Fig.3 Reward of EV charging navigation under different algorithms

为了定量描述不同算法下电动汽车充电引导效果，本文采用最后1000轮迭代的单次充电平均决策次数、平均行驶距离、平均等待时间和平均费用等指标对不同算法进行比较分析，对比结果如表3 所示。从表中可知，就近推荐DIS 算法的单次充电平均决策步数和平均行驶距离均最小，但是由于其只依据最短距离来选择充电目的地和充电路径，而忽略了充电道路行驶速度、充电站电价等因素，从而导致其平均等待时间过长，造成其单次充电平均费用相比于其他算法都高。传统hDQN 算法将电动汽车充电引导问题划分为2 个子问题求解，降低了问题的求解规模，有助于加快计算的求解速度和提升算法的策略搜索能力，因此其单次充电平均费用优于单层DQN 算法和就近推荐DIS 算法。与此同时，所提基于HEDQN 的电动汽车充电引导方法的单次充电平均行驶距离为14.80 km、平均费用为31.77 元，与就近推荐DIS 算法相比，尽管其充电平均行驶距离增加了约20%，但是其平均的充电费用减少了约10%。因此，从以上的分析结果表明了本文所提基于HEDQN 的电动汽车充电引导方法能够在多重不确性因素获得更优的充电引导策略，从而验证了所提方法的有效性。

表3 不同算法下电动汽车充电引导各指标对比Table 3 Comparison of various indicators of EV charging navigation under different algorithms

3.4 基于HEDQN 的电动汽车充电引导环境适应性分析

为了验证本文所提算法的适应性能，现假设22号充电站和32号充电站的电价调换，即设定32号充电站的价格最高。图4 为基于HEDQN 算法在环境发生变换后的电动汽车充电目的地决策损失函数和充电路径决策损失函数值。

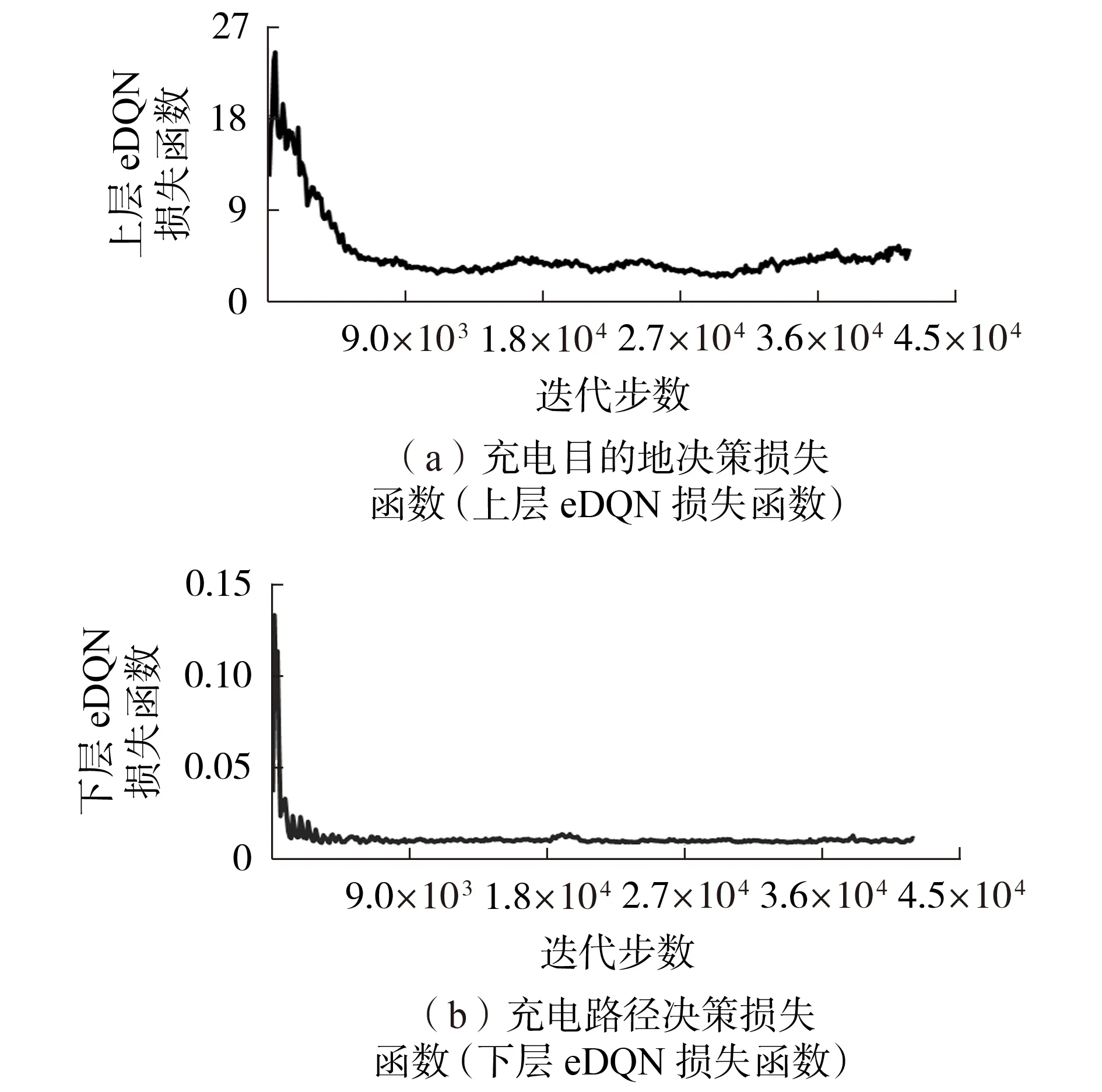
图4 环境发生变化后基于HEDQN算法的电动汽车充电引导损失函数Fig.4 Loss of EV charging navigation based on HEDQN algorithm after simulation environment changes

当环境发生变化后，HEDQN 算法在已有经验的基础上继续学习，从而保证电动汽车充电引导策略的最优性。从图4 中可知，HEDQN 算法在环境发生变化后其损失函数值突增，然后随着算法迭代的进行，只需要经过5 000 步仿真基本收敛，其相比于3.2节随机权重初始的收敛速度提升了10 倍以上，由此验证了本文所提算法的自适应能力。

当环境发生变化后电动汽车在不同地点时选择各充电站的比例如附录B 图B3 所示。通过对比图B2、B3 可知，较多的电动汽车从32 号充电站改换到22 号充电站进行充电。具体地，电动汽车在不同位置选择32 号充电站进行充电的比例从49.20%下降到10.50%；而电动汽车在不同位置选择22 号充电站进行充电的比例从9.20%上升到46.95%。