计及EV负荷-风电异质场景集的交直流混合配电网多目标分布式协同优化

2022-10-15张亚超谢仕炜

电力自动化设备 2022年10期

刘岩，张亚超，朱蜀，谢仕炜

（1. 福州大学电气工程与自动化学院，福建福州 350108；2. 国网湖南省电力有限公司调度控制中心，湖南长沙 410004）

0 引言

在能源系统低碳化转型的背景下，大量直流型分布式电源DG（Distributed Generation）和负荷的接入促进了直流配电网的迅速发展，交直流混合配电网HADDN（Hybrid AC／DC Distribution Network）将成为未来配电网的重要形态［1］。另一方面，电动汽车EV（Electric Vehicle）在减少交通领域的碳排放、缓解能源危机等方面具有巨大的优势和潜能，有望成为未来主要的道路运输工具［2］。随着源侧DG、荷侧EV等分散化资源的大规模接入，传统的集中式优化方法面临着维度灾难、隐私泄露等一系列问题［3］。此外，源-荷侧的双重不确定性和波动性易造成接入节点电压越限频繁问题，依托于传统的无功调整设备难以适应HADDN 的安全经济运行需求［4］。因此，开展计及源-荷双重不确定性的HADDN 有功功率和无功功率的分布式优化运行研究具有重要的意义。

电压源型换流器VSC（Voltage Source Converter）实现了交／直流区域间的常态化双向互联，它不仅能满足有功功率／无功功率连续、精准的控制需求，还能为HADDN 区域间的协调优化提供可能。目前，在HADDN 的优化运行研究中主要采用集中式优化算法，如：文献［4］建立了两阶段鲁棒优化模型对传统无功设备和VSC 进行集中式协调优化；文献［5］提出了一种考虑多种主动管理措施的HADDN集中式调度策略。相比于集中式优化，现有文献对HADDN分布式优化问题的研究相对较少。文献［6］建立了基于目标分析级联法的HADDN 多区域分布式调度模型，文献［7］提出了一种HADDN 分布式电压优化模型，但文献［6-7］所建分布式优化模型中均未考虑源-荷侧的不确定性对系统优化运行的影响。文献［8］建立了考虑风电不确定性的HADDN 鲁棒优化模型，文献［9］提出了计及源-荷双重不确定性的HADDN 分层分布式优化调度模型，其中荷侧的不确定性特指常规负荷。但是随着EV 保有量的快速增长，EV 充电负荷的强随机性愈发突出，因此开展计及EV负荷不确定性的研究尤为关键。

针对EV充电负荷的建模，现有文献大多从时间和空间2个维度展开研究。文献［10-11］采用统计学方法得到EV起始充电时刻、日行驶里程的概率分布函数，利用蒙特卡罗模拟方法生成EV充电负荷场景集，但仅从时间维度分析了EV 的充电行为，对充电负荷时空分布特性的刻画不足。文献［12］通过建立停车概率模型，提出了一种基于EV 行驶、停放特性的充电负荷时空分布预测方法，但未考虑道路流量对车辆行驶的影响。文献［13］建立了基于EV 出行概率矩阵的快充需求时空分布预测模型，但缺乏对EV用户行为特性的分析。

随着DG 渗透率的不断提高，源侧DG 出力与荷侧EV负荷的随机性相互叠加，进一步增加了电力部门的调控难度。目前，关于考虑EV负荷、DG出力不确定性的配电网优化的研究成果较多，如：文献［14］建立了HADDN 中EV 充换储一体站的规划模型，但研究对象侧重于EV充电站，未考虑充电负荷、DG接入对配电网优化调度的影响；文献［15］提出了一种计及风电-EV 不确定性的电力系统节能减排动态调度方案，但对于EV充电负荷不确定性的建模较为简单，缺少对其空间分布特征的刻画；文献［16］提出了一种考虑规模化EV 接入的柔性台区协同经济调度方案；文献［17］构建了计及光储快充一体站的配电网日前经济调度模型。在上述含EV 和DG 的配电网优化调度研究中，仅考虑以经济性最优为目标，但高渗透率下EV负荷、DG出力的不确定性尤为突出，电压越限、网损增加等问题频发，因此亟需开展考虑EV 负荷、DG 出力不确定性的配电网电压质量问题研究。

综上所述，本文建立了计及源-荷侧双重不确定性的HADDN 多目标随机优化模型，并对其进行目标分解和区域解耦，采用基于目标值交换原理的交替方向乘子法（ADMM）实现对所建模型的分布式求解。本文的主要贡献如下：①构建计及EV 充电负荷、风电出力双重不确定性的场景集生成框架，采用基于Wasserstein 距离的0-1 规划模型实现初始场景集的最优缩减；②为了应对源侧DG 出力以及荷侧EV 负荷的不确定性对系统安全经济运行的影响，建立以网络损耗、节点电压偏差最小为目标的HADDN多目标随机优化模型；③通过目标分解和分区解耦，将HADDN 多目标随机优化模型分解为交、直流子区域的单目标优化模型，构建基于目标值交换原理的ADMM分布式优化求解框架。

1 EV充电负荷-风电异质场景集建模

针对EV充电负荷和风电出力的不确定性，利用历史统计数据分别生成EV充电负荷、风电出力场景集，然后对场景进行降维、组合得到EV充电负荷-风电组合场景集及其发生的概率。

1.1 EV充电负荷的时空分布预测模型

EV 充电负荷的时空分布预测模型框架见图1，包括交通路网模型、居民出行模型、EV 时空转移模型3 个部分。首先，根据地理信息数据，建立城市交通路网模型；然后，基于居民出行调查数据，构建不同复杂程度的EV 出行链模型；最后，输入EV 参数，综合城市道路和居民出行信息，以行程时间最短为目标指导EV 的行驶并更新EV 信息，建立EV 时空转移模型。利用蒙特卡罗模拟方法重复抽样，不断更新EV的行驶信息和充电需求，生成考虑时空分布特性的充电负荷场景集。

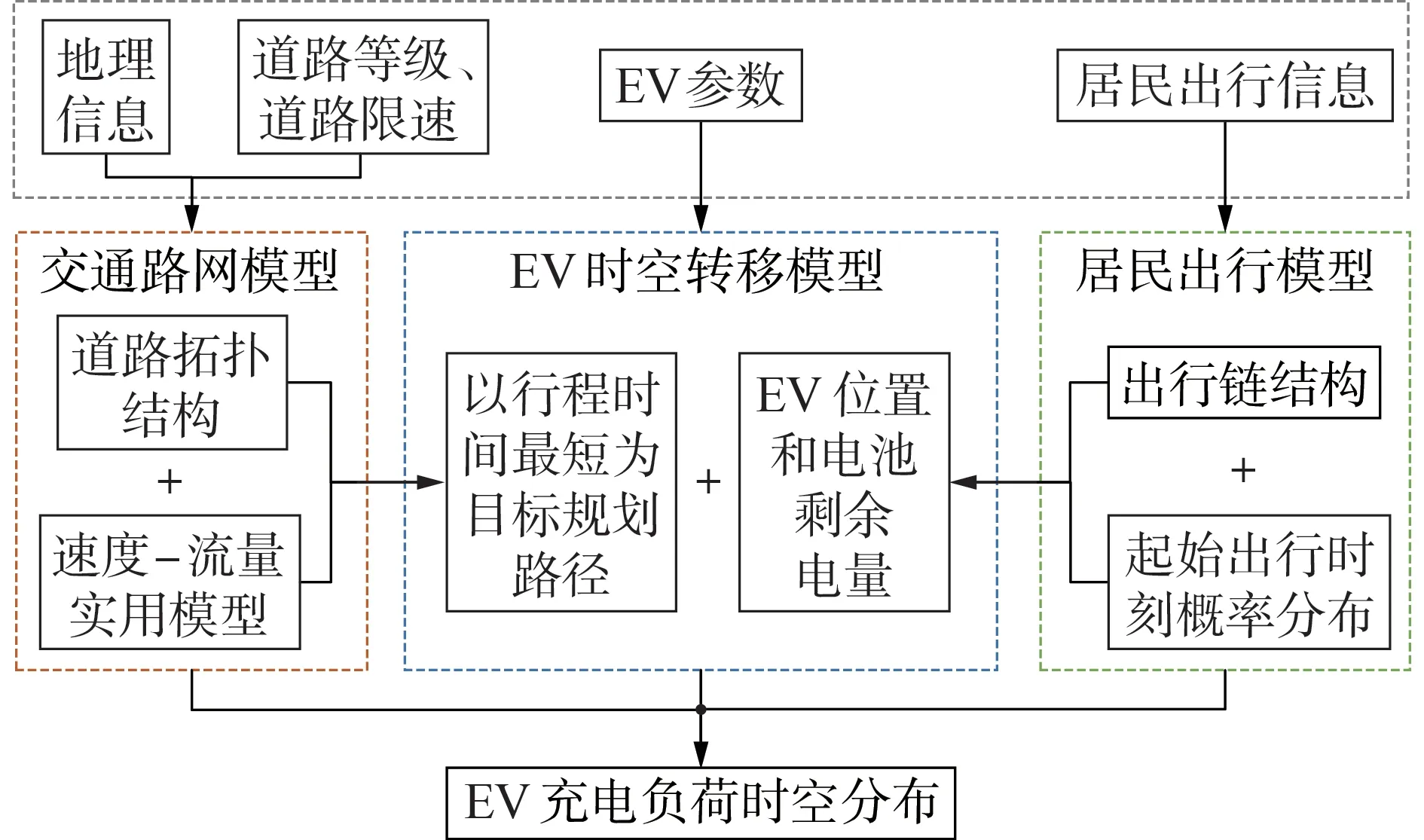
图1 EV充电负荷的时空分布预测模型框架Fig.1 Temporal and spatial distribution predictionmodel framework of EV charging load

1.1.1 交通路网模型

1）道路拓扑结构。

交通路网是研究EV 充电负荷时空分布特性的基础，本文采用图论方法对城市双向交通路网进行建模。交通路网可用图G=(U，E，W)表示，其中U为道路节点集合，E为道路集合，W为道路权重值集合，W可采用道路长度、行驶时间等参数表征道路的量化属性。对含有N个节点的交通路网图G量化赋值，道路邻接矩阵D=[dij]N×N可表示为：

式中：wij为道路ij的权重值。

2）速度-流量实用模型。

在实际的交通出行过程中，EV 用户最关心的路阻因素往往为行程时间，而与行程时间直接相关的EV 行驶速度主要受到道路等级和车流量的限制。因此，本文引入速度-流量实用模型［18］进行分析。

t时段EV 在直连道路ij上的行驶速度vij(t)和通行时间sij(t)可分别表示为：

1.1.2 居民出行模型

1）出行链结构。根据我国传统居民的出行调查数据，本文将出行目的地归纳为住宅（Home，用行程H 表示）、工作（Work，用行程W 表示）、商业（Business，用行程B 表示）这3 类，其中行程B 主要包括购物吃饭和社交娱乐。根据文献［19］中出行链结构的划分规则，用简单链（H-W、B-H）和复杂链（H-W-B-H、H-B-W-H）描述EV用户的出行规律。

2）出行时刻。

根据2016 年英国交通部的统计数据，对不同复杂度出行链的行程起始时刻（即出行时刻）采用不同的分布规律进行拟合，具体分布规律可参考文献［20］设定。

1.1.3 EV时空转移模型

1）EV用户的出行数据。

EV 用户典型的出行数据包括出发地、目的地、出行时刻、返程时刻，这些参数可通过概率分布函数随机抽取；当前位置、荷电状态SOC（State Of Charge）、行驶路径等数据的求解见下文。

2）路径规划。

根据1.1.1 节中的速度-流量实用模型，本文选择行程时间作为道路路阻，以行程时间最短为目标并采用Dijkstra算法实现EV 路径规划。目标函数可表示为：

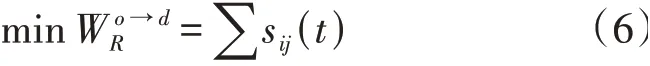
式中：o、d分别为出发地、目的地节点；W o→dR为节点o到节点d之间道路上的行驶时间；R为从节点o到节点d的道路集合。

3）充电负荷时空分布预测。

假设城市功能区内包含足够的充电设施，即EV充电行为不受充电桩位置的影响。假设完整的出行周期为1 d，用lTC，n表示出行链中的第n段行程，每段行程可能经过多条交通道路。当n=0 时，EV 在居民区（即H）内，起始SOCRSOC，0=0.9；当一天的行程结束后，EV 返回居民区充电至SOC 为RSOC，0。可根据式（7）更新EV结束第n段行程时的SOCRSOC，n。

式中：RSOC，n-1为EV 结束第n-1 段行程时的SOC；C为EV 电池容量；ω为EV 行驶1 km 的耗电量；ln为第n段行程的行驶距离。

EV 结束第n段行程后开始充电的条件按照式（8）进行预判，即当下一段行程结束时的SOC 小于0.3时，触发充电需求。

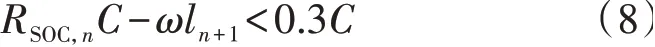
假设EV 结束第n段行程后立刻开始充电，直至SOC 为0.9 或者达到下一段行程的出发时刻。分别根据式（9）和式（10）计算EV 第n段行程的起始充电时刻tstart，n和充电时长tc，n，并根据式（11）计算EVm的充电功率Pm，t。

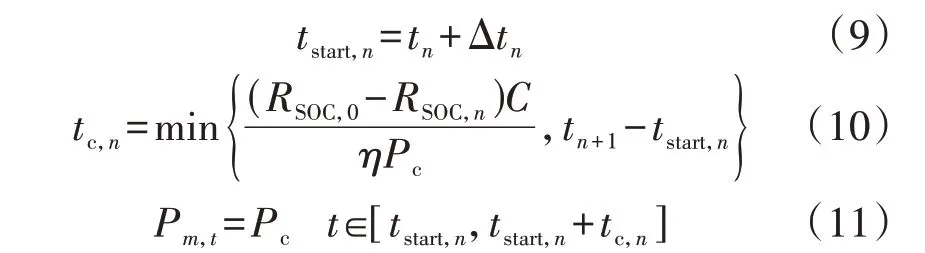
式中：tn为随机抽样得到的第n段行程的起始时刻；Δtn为第n段行程的行驶时间，可由速度-流量实用模型计算得到；Pc为EV 的充电功率；η为EV 的充电效率。

综上所述，可得一天内各统计时段的充电负荷。采用蒙特卡罗模拟方法重复抽样即可生成计及时空分布特性的EV 充电负荷场景集。其中一次蒙特卡罗模拟的流程图见附录A图A1。

1.2 风电预测误差的不确定性建模

风电的实际出力为风电功率预测值与预测误差之和。文献［21］表明，风电预测误差的概率分布受预测出力幅值的影响，且单一概率分布模型无法兼顾风电预测误差概率密度分布尖峰厚尾、非对称的特征。因此，本文采用高斯混合模型对不同功率区间内的风电预测误差进行拟合。风电功率预测框架如图2 所示，风电预测误差不确定性建模的详细过程见附录B。

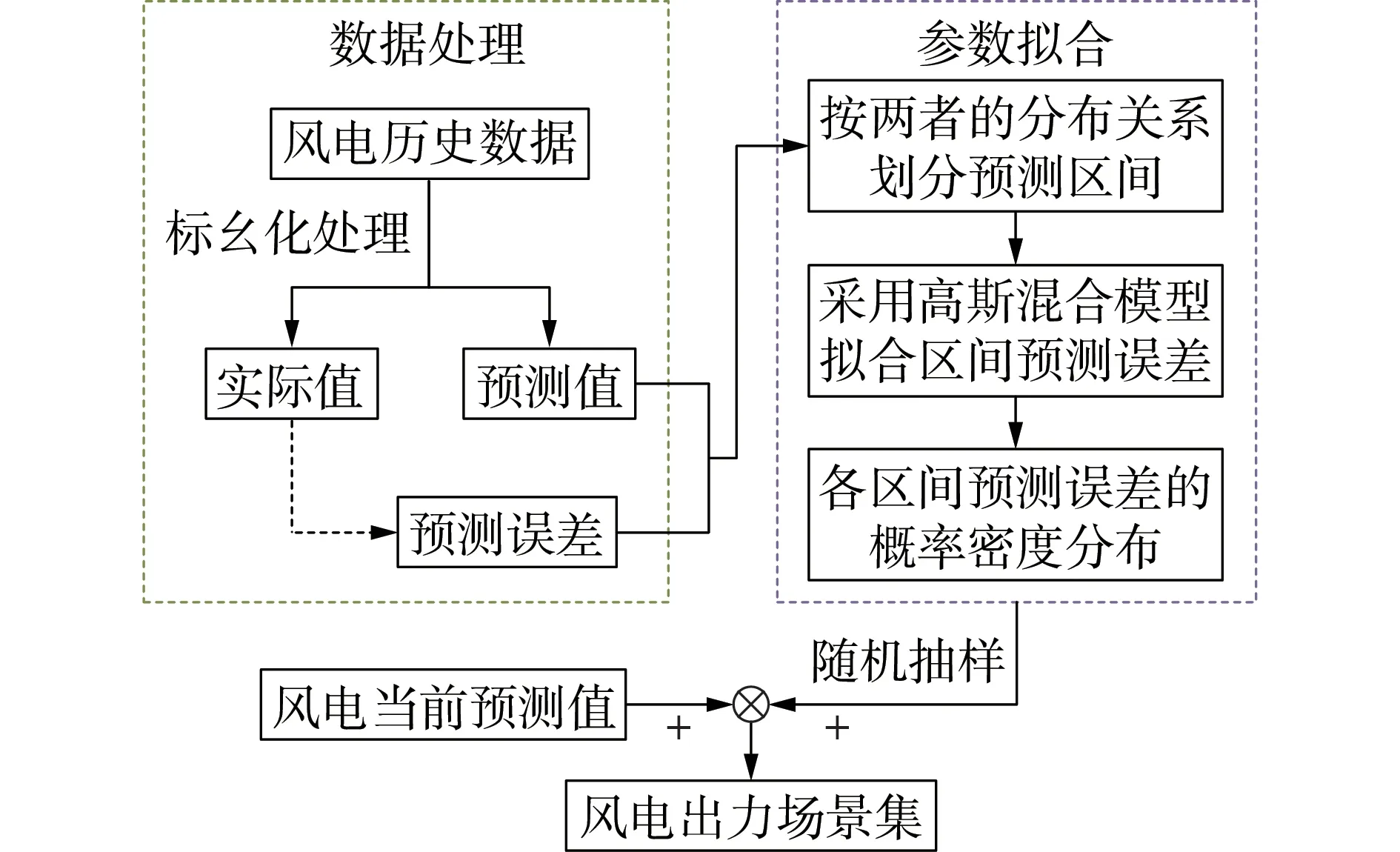
图2 风电功率预测框架Fig.2 Prediction framework of wind power

1.3 基于Wasserstein距离的最优场景缩减

场景缩减是用少量具代表性的典型场景来代替原始的高维场景集，以减轻模型求解的计算负担，其精度在很大程度上依赖于场景间距离的定义［22］。本文引入Wasserstein距离来衡量初始场景与典型场景之间的差距。Wasserstein 距离越小，则缩减后的典型场景集越逼近初始场景集。Wasserstein 距离dW(P，PS)的定义如下：

最优场景缩减过程可视为“选址-分配”双层优化问题，即下层对典型场景进行选择，上层对选取的典型场景进行概率分配，以获得最优的Wasserstein距离。离散域中基于Wasserstein距离的上层概率分配问题可表述为：

式中：Y为给定的典型场景数；yi为0-1 决策变量，若初始场景ζi被选择则yi=1，否则yi=0。

此外，上层问题的求解建立在下层问题的场景确定的基础上，通过添加约束式（15）描述上、下层之间的耦合关系，当且仅当初始场景ζi(ζi∈Ω)被选中即yi=1 时，对应列的决策变量xi，j才可以进行概率分配。

1.4 净负荷场景的生成及削减

根据1.2 节所述方法分别生成NS个EV 充电负荷场景和风电出力场景，经组合后生成N2S个EV 充电负荷-风电组合场景。EV 充电负荷、风电出力组成的净负荷场景如式（18）所示。

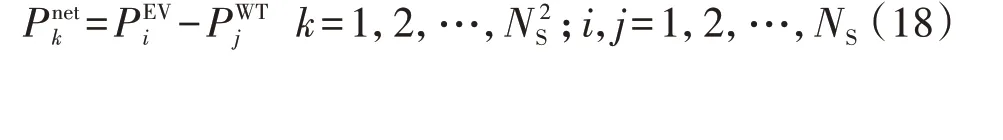
2 HADDN随机优化模型

为了应对EV充电负荷、风电出力的不确定性对HADDN运行的影响，本文建立了基于EV充电负荷-风电组合场景集的随机优化模型。

2.1 目标函数

HADDN 随机优化模型以最小化系统网络损耗和节点电压偏差为优化目标，具体表达式为：

2.2 约束条件

1）风机出力约束。

接入交流侧的风机有功、无功出力约束分别如式（22）和式（23）所示，接入直流侧的风机则不包含无功出力约束。

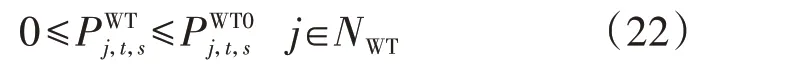
此外，HADDN 随机优化模型还需要满足交／直流二阶锥潮流约束、储能系统（ESS）的运行约束以及换流站的运行约束，具体如附录C 式（C2）—（C21）所示。

3 基于ADMM的多目标分区优化模型

为了减轻交直流区域的数据通信压力，保护区域信息隐私，实现分区自治，本文采用基于目标值交换原理的ADMM求解HADDN多目标优化模型。

3.1 多目标分区解耦机制

1）将第2 节建立的集中式HADDN 多目标优化模型转化为单目标模型，如附录D 式（D1）—（D4）所示，具体步骤见附录D。

2）采用线路撕裂法，将换流站与直流配电网之间的直流联络线撕裂，解耦得到2 个独立的子区域A、B，如附录D图D1所示。

分区解耦后，子区域A、B需添加功率、电压以及目标函数值的一致性约束，具体可表示为：

3.2 分布式优化

对优化问题式（D5）的目标函数值取相反数，将其转化为最小化问题，并将式（28）以惩罚项的形式添加到优化问题中，根据ADMM 的原理，可得到解耦后子区域A、B 的优化模型分别如附录D 式（D6）和式（D7）所示。基于ADMM 的分布式调度求解步骤见附录E。

4 算例分析

为了验证本文所建模型的有效性，在MATLAB R2017b平台上利用YALMIP工具箱以及CPLEX求解器建模求解，硬件环境为AMDRyzen 7 4800HCPU @2.90 GHz，16 G内存。

4.1 基本数据设置

本文算例测试系统的拓扑结构如附录F 图F1所示，交流配电网采用改进的IEEE 33 节点网络，直流配电网采用文献［23］中的15 节点算例测试系统，两者通过换流站相连接。交通网络采用29 节点道路拓扑结构，相关道路参数见文献［18］。充电站建在交通网络的4个区域（居民区1、居民区2、工作区、商业区）内，且分别接入交、直流配电网的4 个节点，以实现电气-交通网络的耦合。

交流配电网的额定电压为15 kV，直流配电网的额定电压为10 kV，两配电网电压幅值的最大波动范围为［0.95，1.05］p.u.；交、直流配电网中支路允许通过的最大电流分别为500、800 A，变电站关口以及支路传输的有功、无功功率上下限分别为±9 MW和±6 Mvar。交、直流配电网的基本负荷曲线见附录F 图F2，并将无功负荷数值设置为有功负荷数值的50%。接入HADDN 的设备有风电机组、EV充电桩、ESS、SVG，其基本参数设置见附录F 表F1—F3。本文采用蒙特卡罗模拟方法分别生成500 个EV 充电负荷、风电出力场景，经净负荷场景生成及缩减后得到5个EV充电负荷-风电典型场景集。

交通网络拓扑被划分为居民区1（含节点1—11）、居民区2（含节点12—16）、工作区（含节点17—20、22、27）和商业区（含节点21、23—26、28、29）。4个区域内共有1200辆EV，各EV 用户按一定的概率选择出行链，具体见附录F表F4。EV 电池的额定容量为30 kW·h，充电SOC 上限为0.9，充电需求触发SOC 阈值为0.3；EV 在居民区内进行慢速充电，在工作区和商业区内进行快速充电，慢充、快充功率分别为15、30 kW；EV 行驶1 km 的耗电量取值见附录F表F5。

4.2 仿真结果分析

4.2.1 EV充电负荷的时空分布特征

为了验证本文所建EV 充电负荷时空分布模型的有效性，本节以某EV 充电负荷场景为例展开分析。

首先以某辆EV 的全天行程为例，说明EV 时空转移特性对充电负荷时空分布的影响，具体结果如附录G 图G1 所示。图G1（a）中，每条黑色线段代表EV 的时空转移轨迹，其向x-y平面的投影（紫色线段）为EV 的实际行驶路线。由图可知：EV 从居民区节点12出发到达商业区节点21，停留15 min 后前往工作区节点20 上班，在节点20 处的SOC 满足式（8）所示充电需求触发条件即开始充电，在充电时段内该节点会累积部分充电负荷；下班后，EV 返回居民区，且为了保证第二天的正常行驶而进行充电，同样会导致节点12处充电负荷增加。

进一步以1 h 为仿真步长（即全天24 h 被分为24 个时段），统计各区域全天24 h 内EV 触发充电需求的分布情况，结果如图3所示。

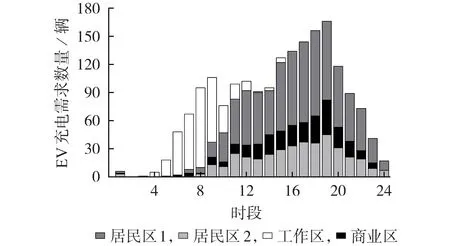
图3 各区域的EV充电需求分布Fig.3 EV charging demand distribution in each region

由图3 可知，不同区域的EV 充电需求数量在时间上分布不均衡。由于EV 在结束一天的行程后需返回住宅充电，故在时段17—21 内居民区1、居民区2 出现了充电需求高峰，共有587 辆EV 产生充电需求；工作区以工作出行为目的，EV 充电需求高峰集中在上班的时段7—10 内，总需求为288 辆；商业区以娱乐出行为主，充电需求高峰时段的跨度较长，主要集中在时段12—21。可见，EV 时空转移特性会导致各区域内EV充电需求的时间分布不均衡，使得该场景下的充电负荷峰谷差明显，呈现“双峰”特性。

EV 充电负荷的时空分布情况如附录G 图G2所示。由图可知：由于EV用户集中在工作时段进行充电，因此工作区（含节点17—20、22、27）在时段7—10 内有明显的负荷高峰，峰值为1.025 MW；用户结束行程后返回居民区（含节点1—16）充电，在16:00—20:00 时段内会累积另一个负荷高峰，峰值达到1.56 MW；商业区的EV充电负荷则较为分散。

4.2.2 场景缩减算法的性能分析

为了验证基于Wasserstein距离的最优场景缩减算法的有效性，定义式（29）所示距离指标Tg来衡量本文所用场景缩减算法与传统同步回代消减法所得典型场景集对初始场景集的逼近程度。Tg值越小，则缩减后的典型场景集越逼近初始场景集。

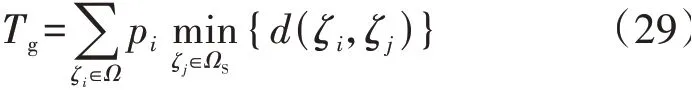
根据第1 节的场景建模方法，分别生成300 个、500 个净负荷场景，经基于Wasserstein 距离的最优场景缩减算法、传统同步回代消减法缩减后的结果对比见附录G 表G1。由表可知，本文所用场景缩减算法的距离指标Tg值较小，即缩减后的典型场景集更能代表初始场景集。此外，本文所用场景缩减算法的求解速度较传统同步回代消减法更优，且随着场景数量规模的扩大，该优势愈加明显。

4.2.3 优化调度结果分析

1）优化策略性能分析。

为了验证本文所提方法的有效性，设置如下3种模式进行对比分析：①模式1，不考虑ESS、SVG 的接入以及DG、VSC 的无功调节能力，VSC 采用下垂控制策略，对系统进行有功功率优化；②模式2，考虑ESS、SVG 的接入以及DG、VSC 的无功调节能力，VSC 采用下垂控制策略，对系统进行有功功率和无功功率协调优化；③模式3，考虑ESS、SVG 的接入以及DG、VSC 的无功调节能力，VSC 采用主从控制策略，对系统进行有功功率和无功功率协调优化。

上述3种模式的优化结果如表1所示，表中节点电压偏差、电压波动范围均为标幺值，后同。由表可知，考虑多设备间的协调优化后，相较于模式1，模式2 的网络损耗减小，节点电压偏差减小了46.0%，系统节点最高电压从1.0401 p.u.降低为1.0179 p.u.，验证了本文所提方法的有效性。此外，对比模式2和模式3 的结果可知，VSC 采用下垂控制和主从控制时，系统的网络损耗、节点电压偏差的优化效果基本一致。3 种模式下配电网的节点电压分布结果见附录G图G3。

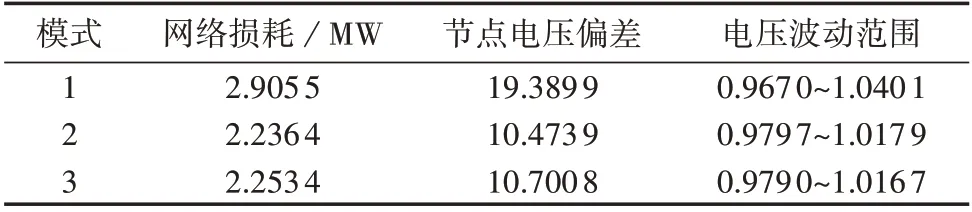
表1 3种模式的优化结果Table 1 Optimization results of three modes

以12:00 时刻为例，模式2 和模式3 下各换流站向直流侧传输的有功功率结果如表2 所示。交流配电网通过VSC1和VSC2向直流配电网供电，其中VSC1靠近交流配电网的首端，承担向直流配电网供电的主要任务。VSC3将直流侧的有功功率转送至交流侧，避免了有功功率在交流网络中的长距离输送，有利于减小网络损耗。在模式3 下，主换流站VSC1负责维持直流电压稳定和平衡系统功率，因此VSC1输送的功率较大。采用下垂控制时各VSC 根据下垂斜率方程共同承担功率平衡，通过调节直流电压来控制功率大小。因此相比于模式3，模式2下VSC1承担的有功功率减少，VSC2和VSC3传输的有功功率增大。

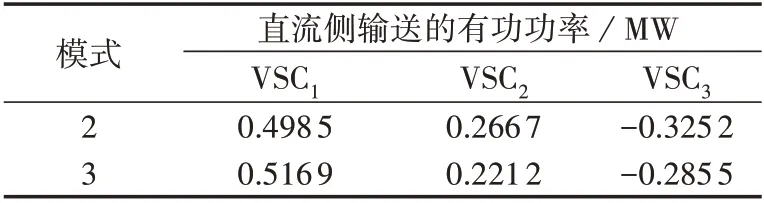
表2 换流站直流侧输送的有功功率Table 2 Active power transmitted by DC side of converter station

结合表1 和2 可知，在不同的VSC 控制方式下，本文所提优化策略均能取得良好的优化效果。

2）不同运行方案的潮流分析。

以模式2 为例，为了进一步分析EV 充电负荷接入系统后，调节ESS、SVG、VSC对电网电压的支撑作用，设置以下4 种运行方案：①方案1 不考虑ESS、SVG、VSC 的无功调节能力，系统接入基准EV 充电负荷；②方案2—4 均考虑ESS、SVG、VSC 的无功调节能力，且方案2中系统不接入EV 充电负荷，方案3中系统接入基准EV 充电负荷，方案4 中系统接入的EV充电负荷为基准值的1.5倍。

4 种运行方案下居民区1 充电站即交流节点24的电压曲线如图4 所示，图中电压为标幺值。由图可知：由于方案1 不考虑各设备的无功调节能力，交流侧节点25 处的风机出力大于本地负荷，会发生功率倒送，导致节点24 的电压大幅升高；同时根据上文EV 充电负荷时空分布特性的分析，居民区1 的充电负荷高峰集中在16:00—20:00 时段，此时风电消纳量增大，使得方案1 下该时段内的电压有明显下降。此外，随着EV 充电负荷接入比例的不断增加，高峰时段的EV充电需求激增。为了减小负荷峰谷差、提高风电利用率，在EV 充电负荷低谷时段（00:00—10:00），大量风电功率向ESS 倒送，导致方案2—4下该时段内的节点电压逐渐升高。

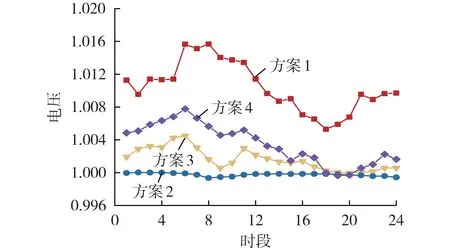
图4 交流节点24的电压曲线Fig.4 Voltage curve of AC Node 24

方案3 的ESS 有功、无功功率结果如附录G 图G4 所示，其中功率值大于0 表示吸收功率，值小于0表示发出功率。结合图4分析可知：方案3中配置的ESS 在负荷低谷时段吸收系统中的无功功率，缓解了风电功率倒送引起的节点电压升高情况；ESS 在负荷高峰时段发出无功功率，防止电压降落，起到了抑制节点电压波动的作用。同时，ESS 在负荷低谷时段吸收有功功率，在负荷高峰时段发出有功功率，起到了减小负荷峰谷差、降低网络损耗的作用。

工作区充电站即交流节点10 的电压曲线以及ESS 的工作情况见附录G 图G5。由图可知，接入EV充电负荷之后，各方案的节点电压在07:00—10:00时段内均有明显下降，符合EV用户普遍选择到达工作地后进行充电的行为特性。ESS 接入后，在负荷低谷时段（00:00—05:00）吸收有功功率，在EV 充电负荷高峰时段发出有功功率以满足充电需求，并发出大量的无功功率以防止节点电压过低，起到了无功补偿和削峰填谷的作用。

3）ADMM的有效性分析。

为了验证本文所用分布式优化方法的有效性，以模式3 为例，分别采用集中式、分布式优化方法求解HADDN 优化问题，结果如表3 所示。由表可知，ADMM 求解所得网络损耗、节点电压偏差与集中式方法所得结果基本一致，验证了ADMM 的有效性。分布式优化和集中式优化的残差迭代过程见附录G图G6。由图可知：分布式优化经过34次迭代后残差达到收敛裕度5×10-3，用时463.365 s；集中式优化由于不需要迭代计算，其求解时间为152.459 s。考虑到本文属于日前优化调度问题，虽然分布式优化方法的求解时间相对较长，但仍在可接受的范围内。故相比于集中式优化方法，分布式优化方法在牺牲了一定的求解时间的条件下实现了对优化问题的解耦和对隐私的保障［24］。

表3 集中式优化方法与分布式优化方法的计算结果对比Table 3 Comparison of calculation results between centralized and distributed optimization methods

4）二阶锥松弛精度分析。

当优化问题的目标函数为支路电流的严格增函数［25］时，二阶锥松弛精度得以保证。考虑到本文的优化目标包含节点电压偏差项，可能导致二阶锥松弛不精确。以ADMM 的迭代求解结果对二阶锥松弛精度进行验证［5］，其误差散点图见附录G 图G7。由图可知，最大松弛误差为4.5884×10-4，满足二阶锥松弛精度要求。