基于六轴机器人的BRDF绝对测量装置标校方法研究

斯鹏飞,张黎明,黄文薪,陈洪耀,李佳伟,张志远,杨宝云,王戟翔

(1中国科学院合肥物质科学研究院安徽光学精密机械研究所通用光学定标与表征技术重点实验室,安徽 合肥 230031;2中国科学技术大学,安徽 合肥 230026)

0 引言

基于星上定标是地球观测卫星委员会(CEOS)下属的定标与数据确认工作组(WGCV)优先推荐的定标方式,也是地球观测卫星必须具备的定标方式。特别地,基于太阳-漫射板的星上定标方法可以实现遥感器全光路、全视场、端到端的高频次、高精度定标[1,2],而漫反射板的双向反射分布函数(BRDF)是影响光学遥感器星上定标精度的关键因素之一,提高漫反射板的BRDF测量不确定度将直接提高光学遥感器星上定标的精度。物体的BRDF测量通常采用和漫反射参照标准板(白板)比对测量的方法,因此,提高漫反射参照标准板的BRDF绝对测量精度有助于BRDF测量相关研究领域水平的提高,具有重要的应用价值。

目前,无论是美国国家标准与技术研究院(NIST)和德国联邦物理技术研究院(PTB)等机构相继研制的BRDF绝对测量装置[3-8],还是国内中国科学院安徽光学精密机械研究所和长春光学精密机械与物理研究所相继研制的BRDF绝对测量装置[9-11],转角的不确定度都是整个装置不确定度的主要来源之一。为获得较低的转角不确定度,需要建立实验室坐标系与样品转动机构坐标系之间的关系,以及调整光源或探测器转动中心与漫反射板转动中心重合,即对BRDF测量装置进行标校。而对于BRDF测量装置的标校方法,在国内外尚未见报导。

本文针对BRDF绝对测量装置转角不确定度贡献较高的问题,根据装置的旋转特点,通过固定于中空分度盘上的积分球光源,利用其出射的中央法向光束建立标校模型,解算出坐标系之间的变换关系,确定了各部件空间相对几何关系,旨在降低转角的不确定度,从而降低BRDF绝对测量不确定度。

1 BRDF绝对测量装置实现原理

1.1 BRDF绝对测量装置结构

研制的BRDF绝对测量装置由高亮度高均匀性积分球光源(光源系统)、样品转动和光源回转机构(转角机构)以及光谱辐射测量单元(探测系统)组成[9],如图1所示。其中转角机构由中空分度盘与串联式六轴机器人组成,其部分参数分别如表1、2所示。光源系统由高亮度高均匀性积分球和调节机构组成。在标校过程中,将积分球球口出光筒卸载,使用激光器安装夹具将激光器安装在积分球球口,通过夹具与球口的机械加工装配保证激光器出射的光束与积分球中央法线一致,即以激光束代表积分球光源中央法线方向。

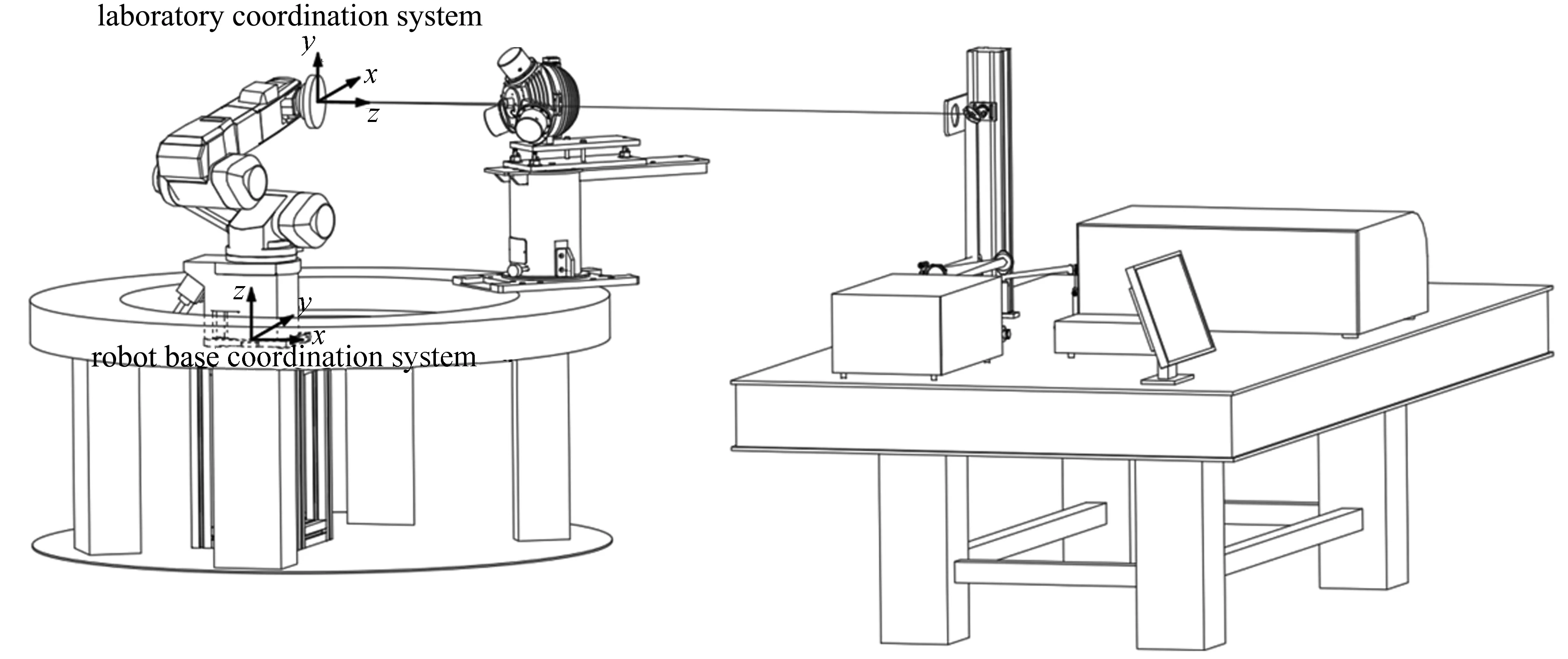
图1 BRDF绝对测量装置Fig.1 Absolute measurement device of BRDF

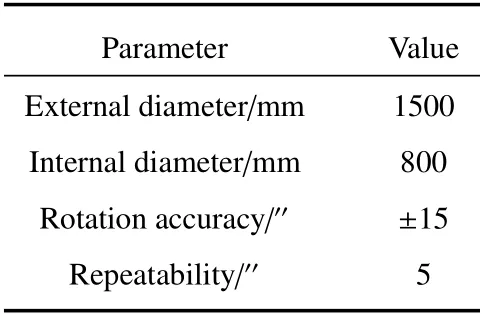
表1 中空分度盘部分参数Table 1 Partial parameters of middle space indexing disk

表2 六轴机器人部分参数Table 2 Partial parameters of six-axis robot

1.2 相关坐标系定义及关系

机器人基坐标系是以机器人底座上某一点的位置为原点建立坐标系,固连于底座。在右手直角坐标系中,实验室坐标系以中空分度盘转轴轴线与光源中央法线交点为原点建立坐标系,Z轴沿中空分度盘轴线向上,X轴沿着测量时观测方向即与光源为0°时中央法线方向相反。漫反射板坐标系即为BRDF定义中所涉及的坐标系。机器人工具坐标系[12,13]默认以机器人末端法兰中心为原点,XYZ轴与基坐标系一致,之后随机器人位置与姿态变动。各坐标系关系如图1所示,图中实验室坐标系、漫反射板坐标系以及机器人工具坐标系处于重合状态。

1.3 实现原理

基于均匀的积分球辐亮度面光源,物体的BRDF定义式可转换为[1]

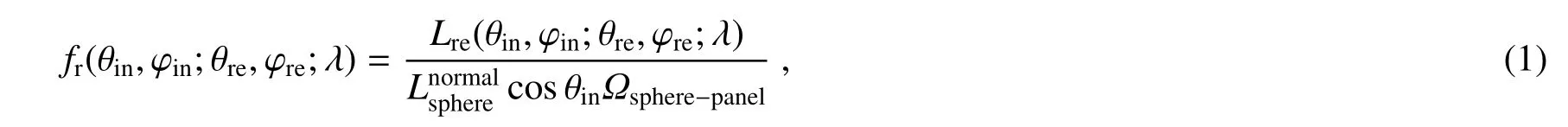
式中:fr分别表示BRDF值,θin、θre、φin、φre表示漫反射板坐标系定义的四个角度,Lre表示在(θin、θre、φin、φre)上的辐亮度,表示积分球出射的辐亮度,Ωsphere-panel表示积分球到漫反射板的立体角。根据(1)式,漫反射板等漫反射参照体的绝对BRDF测量可通过对积分球辐亮度、漫反射样品反射辐亮度以及照明几何立体角的测量完成。

在漫反射板坐标系和实验室坐标系中,入射矢量和反射矢量分别表示为

式中:Si、Sr分别表示入射和反射矢量,θi、θr、φi、φr表示漫反射板坐标系定义的四个角度,δ表示中空分度盘负载光源转动的角度,上标panel表示在漫反射板坐标系下,lab表示在实验室坐标系下,下同。

在进行漫反射板等漫反射参照体的BRDF绝对测量之前,光源、漫反射板预先到达测量零点,然后由机器人带动漫反射板定点三维旋转,同时中空分度盘带动光源进行一维旋转来构建BRDF测量所需的角度条件。而机器人与中空分度盘运动定位所需几何参数和BRDF定义涉及的角度不一致,因此需要对BRDF角度参数与转角机构的运动定位参数进行转换,即

式中α、β、γ表示实验室坐标系以y→x′→z′′的顺序绕各轴相应转动的角度。

由(2)、(3)式的矢量关系可解得[9]

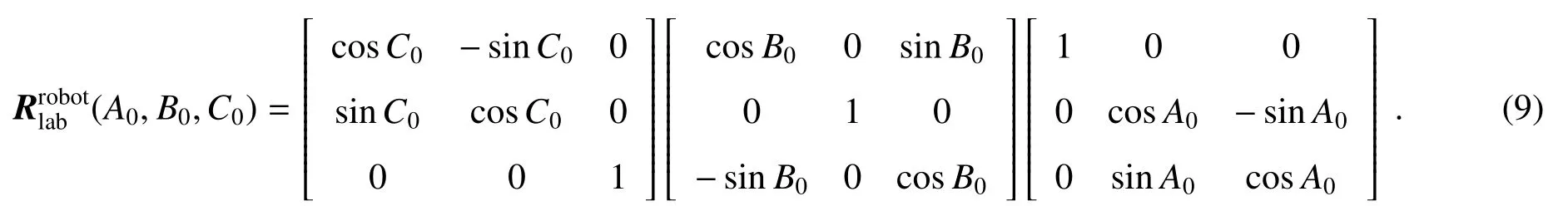
实验室坐标系与机器人基坐标系关系可表示为

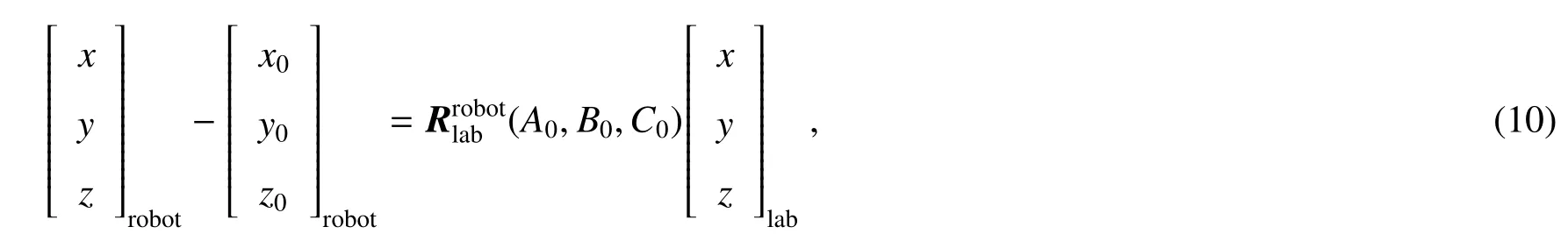
式中(x0,y0,z0)T表示实验室坐标系原点在机器人基坐标系下的坐标。

由(2)～(10)式可以看到,在对BRDF角度参数与转角结构运动定位参数进行转换时,(5)～(8)式成立需满足(4)和(10)式所设定的关系,即有准确的测量零点。由(4)～(10)式可以看到,实验室坐标系在机器人基坐标系下的位置(x0,y0,z0)T、姿态(A0,B0,C0)T直接影响转角的不确定度,故高精度的实验室坐标系位置(x0,y0,z0)T与姿态(A0,B0,C0)T的确定是获得高精度BRDF测量所需角度的保证。

因此,综上所述,BRDF绝对测量装置标校需要完成以下内容:1)确定实验坐标系原点位置以及坐标轴方向,即与机器人基坐标系建立准确的关系;2)光源中央法线沿中空分度盘旋转半径方向且与其转轴正交;3)装置标校精度验证。

2 标校原理

BRDF绝对测量装置的标校主要由三个过程组成:中空分度盘转轴轴线方程及初步坐标系变换关系的建立,积分球法向光束调整与实验室坐标系原点确定及坐标系变换关系确定,以及基于镜反射的装置转角精度检验。

2.1 中空分度盘转轴轴线方程及初步坐标系变换关系建立

根据BRDF绝对测量装置的特点,以机器人为测量工具,固定于中空分度盘的积分球中央法向光束为指示,通过对中空分度盘旋转的光束空间位置测量与分析获取中空分度盘转轴的空间直线方程,初步建立实验室坐标系与机器人基坐标系之间的变换关系。

以机器人工具坐标系原点(其在机器人基坐标系下的值可直接读出)为参考,测量不同光源角度下激光束的2个点,得到不同角度激光束在机器人基坐标系下的坐标[x1(δi),y1(δi),z1(δi)]T、[x2(δi),y2(δi),z2(δi)]T,如图2(a)所示。转动中空分度盘,使积分球处在不同角度,如图2(b)所示,其中还标示了距离实验室坐标系原点半径为r且处在激光束上的点(a点),其中实线表示激光束,虚线表示激光束上转动半径为r的点,即a点与圆心的连线。

图2 (a)利用机器人测量激光束矢量;(b)转动中空分度盘使积分球处于不同角度Fig.2(a)Measurement of laser beam vector by robot;(b)Rotate the hollow dividing disc to make the integrating sphere at different angles

基于各个角度的激光束测量点,有直线方程

当激光束与机器人基坐标系Y轴平行或接近平行时,激光束上点X坐标值变化很小,这会给(11)式的计算带来较大的误差,可以使用等式

进行计算。

设光源角度为δi时,a点与实验室坐标系原点构成的矢量在实验室坐标系跟随光源旋转后的坐标系下表示为[0,0,1]T,则

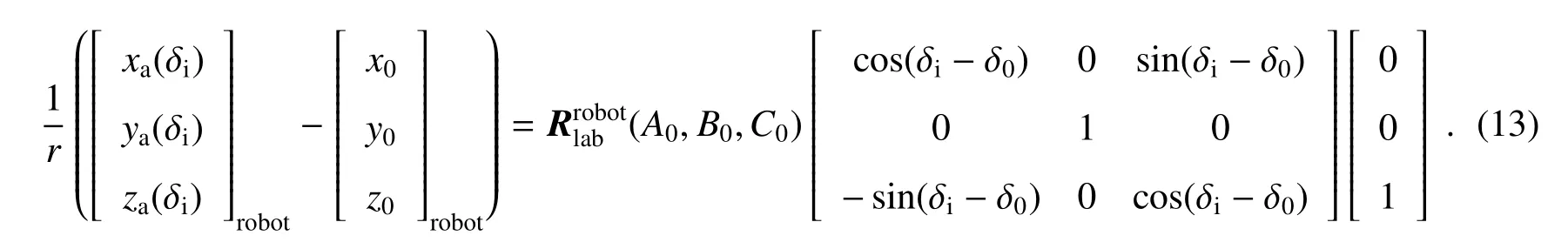
为了保证光源处于任意角度时r点与实验室坐标系原点的连线与中空分度盘轴线垂直,任意两个光源角度的a点与实验室坐标系原点构成的矢量平面的法线应与中空分度盘轴线平行,设中空分度盘转轴轴线在实验室坐标系下表示为[0,1,0]T,即

联立(11)～(14)式,优化求解可以得到实验室坐标系原点在机器人基坐标系下的坐标[x0,y0,z0]T、实验室坐标系与机器人基坐标系之间的变换关系(A0,B0,C0)以及a点在各个角度时在机器人基坐标系下的坐标[xa(δi),ya(δi),za(δi)]T。

根据中空分度盘转轴轴线与a点到转动中心的连线互相垂直这一关系,可以获得中空分度盘转轴轴线方程

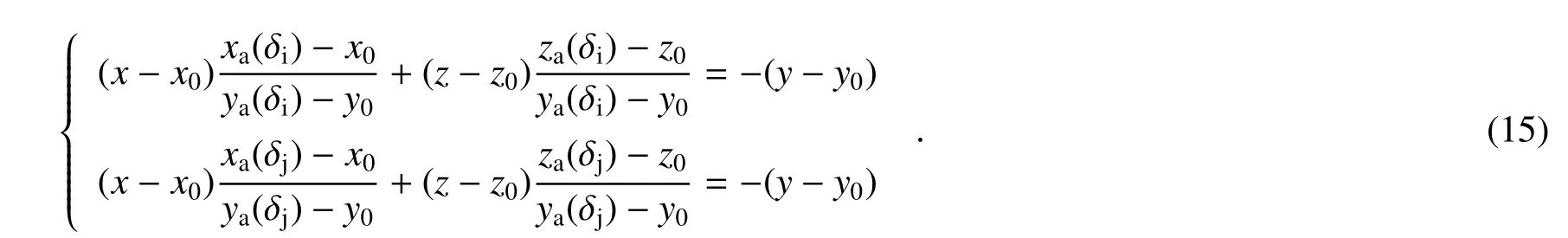
当积分球高度改变即z0改变时,可确定相应的[x0,y0]T。

2.2 积分球法向光束调整与实验室坐标系原点确定及坐标系变换关系确定

在上述测量分析的基础上,以工具坐标系Y轴为参考,基于镜反射原理调整积分球,当切入平面反射镜后,紧贴机器人末端的反射镜法向与中空分度盘的转轴垂直;且积分球指向光束调整后的镜反射可原路返回时,积分球出口中央法向与中空分度盘转轴相互垂直。然后根据激光束入射在Y轴上的位置和转轴方程重新计算圆心位置,调整机器人末端位置使激光束入射在机器人末端中心,此时积分球出口中央法向与中空分度盘转轴相互垂直且相交(交点即为实验室坐标系原点)。

2.2.1中空分度盘转轴的标示

在进行积分球调整之前,需要将工具坐标系Y轴转动到与中空分度盘转轴轴线重合,以标示出中空分度盘的转轴,这样才能目视观测以确保光束与转轴相交。之后紧贴机器人末端切入平面反射镜,其法向与中空分度盘的转轴垂直。

2.2.2 积分球及机器人调整

控制机器人末端姿态,转动中空分度盘,调整积分球方位及俯仰,直至:1)激光束入射在工具坐标系Y轴上;2)切入平面反射镜,激光束可原路返回。当光束已对准Y轴且镜反射可原路返回后,根据激光束入射在Y轴上的位置和转轴方程重新计算圆心位置,控制机器人末端位置到圆心,中空分度盘相对旋转±90°,激光束始终入射夹具表面中心,如图3所示。

图3 光源相对旋转±90°Fig.3 Relative rotation±90° of light source

2.2.3 坐标系变换关系建立测量

重新测量光束矢量以及各光束对应的光源实际角度,为最终建立实验室坐标系与机器人基坐标系之间的变换关系做准备。根据前面的标校模型重新计算(x0,y0,z0)T、(A0,B0,C0)T。

2.2.4坐标系变换关系确定与反射光路调整

根据机器人、中空分度盘上积分球位置、反射测量光路位置关系,定义中空分度盘零点位置与实验室坐标系,最终分析确定实验室坐标系与机器人坐标系之间的变换关系,并据此调整BRDF反射测量系统光路。

2.3 基于镜反射测量验证转角不确定度

本研究采用了镜反射测量来验证转角不确定度,即以平面镜代替漫反射板,光源为180°时的入射光束为基准,观察光源处于其他角度时的反射光束与基准的偏差。

当发生镜反射时,有

结合(5)～(8)式,镜反射测量时运动定位参数可简化为

以光源处于180°时的入射光束为基准,即入射在位于探测方向的坐标纸原点上,如图4所示。镜反射测量时,反射光束在坐标纸上的光斑中心若不在原点,则为转角误差。设坐标纸与实验室坐标系原点距离为dmm,反射光束光斑在坐标纸上的坐标为[xi,yi]T,则转角不确定度可表示为

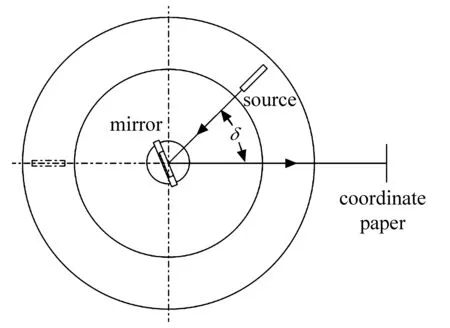
图4 镜反射测量示意图Fig.4 Schematic diagram of mirror reflection measurement

入射角的BRDF相对误差可表示为

3 实验结果与讨论

3.1 转角系统调整结果

利用机器人测量不同角度的激光束以进行标校实验,第一次测量的原始数据如表3所示,以坐标值的形式展示。图5为不同角度激光束上的点在机器人基坐标系XY平面上的投影图,其中X轴表示投影点与机器人基坐标系Y轴的距离,Y轴表示投影点与机器人基坐标系X轴的距离,各条线的右端点处已标明光源所处角度。

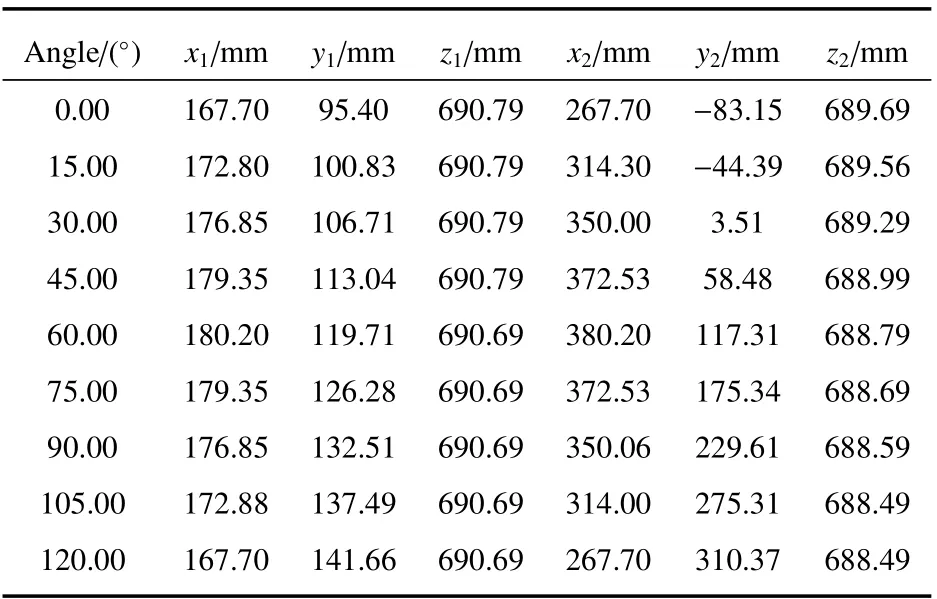
表3 不同角度激光束上点测试数据(第一次测试)Table 3 Test data of laser beam on different angles(The first test)

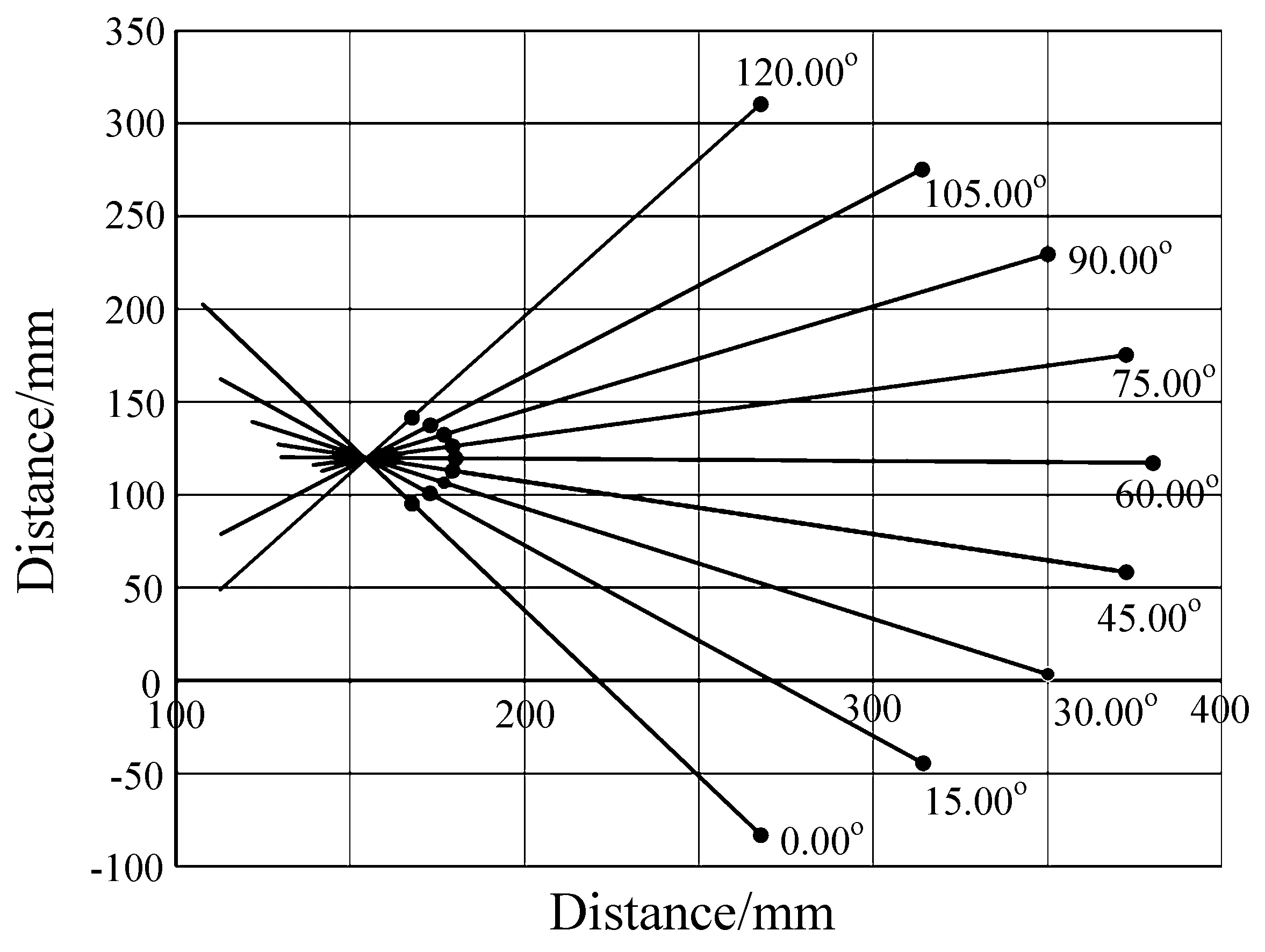
图5 第一次测试数据XY平面投影图Fig.5 XY plane projection of the first test data

由表3数据,根据(11)～(14)式优化求解得到的结果如表4、表5所示,优化求解时误差平方和为0.0001。根据表4,实验室坐标系与机器人基坐标系的变换关系即光源60°时机器人对应的姿态为(90.15°,0.39°,89.21°),据此姿态和计算得到的实验室坐标系原点位置调整积分球,然后测量激光束在Y轴上点与原点的距离以确定z的坐标,将表5中的a点坐标代入转轴方程(15)确定x、y,此时得到的(x,y,z)T即为新的实验室坐标系原点。

表4 实验室坐标系原点位置以及与机器人基坐标系变换角度(第一次测试)Table 4 Origin position of the laboratory coordinate system and the transformation angle with the robot base-coordinate system(The first test)

表5 激光束上a点坐标(r=629.5 mm,第一次测试)Table 5 Coordinates of point a on laser beam(r=629.5 mm,The first test)

积分球调整结束后,利用机器人重新测量激光束,第二次测量的原始数据如表6所示,以坐标值的形式展示。图6(a)为不同角度激光束上的点在机器人基坐标系XY平面上的投影图,其中X轴表示投影点与机器人基坐标系Y轴的距离,Y轴表示投影点与机器人基坐标系X轴的距离,各条线的右端点处已标明光源所处角度。图6(b)为激光束交点处局部放大图,可以看到多条光束已经基本交于一点,具体表现为任意两条光束都交于半径为0.2 mm的圆内,此时认为光源中央法向光束已调整到沿中空分度盘径向。为最终确定实验室坐标系与机器人基坐标系之间的关系,测量了各光束对应的实际光源角度(即切入反射镜能原路返回),数据如表7第二列所示。根据表7,选取光源实际角度为60.00°时的中央法线方向为实验室坐标系X轴,即测量时的观测方向,表8中[x0,y0,z0]T即实验室坐标系原点在机器人基坐标系下的坐标,以此确定实验室坐标系位置,(A0,B0,C0)为实验室坐标系与机器人基坐标系的变换关系。

图6 (a)第二次测试数据XY平面投影图;(b)交点局部放大图Fig.6(a)XY plane projection of the second test data;(b)Local enlarged view of intersection

表6 不同角度激光束上点测试数据(第二次测试)Table 6 Test data of laser beam on different angles(The second test)

由表6数据,根据(11)～(14)式,求解得到的结果如表7、表8所示,优化求解时误差平方和为0.0007。

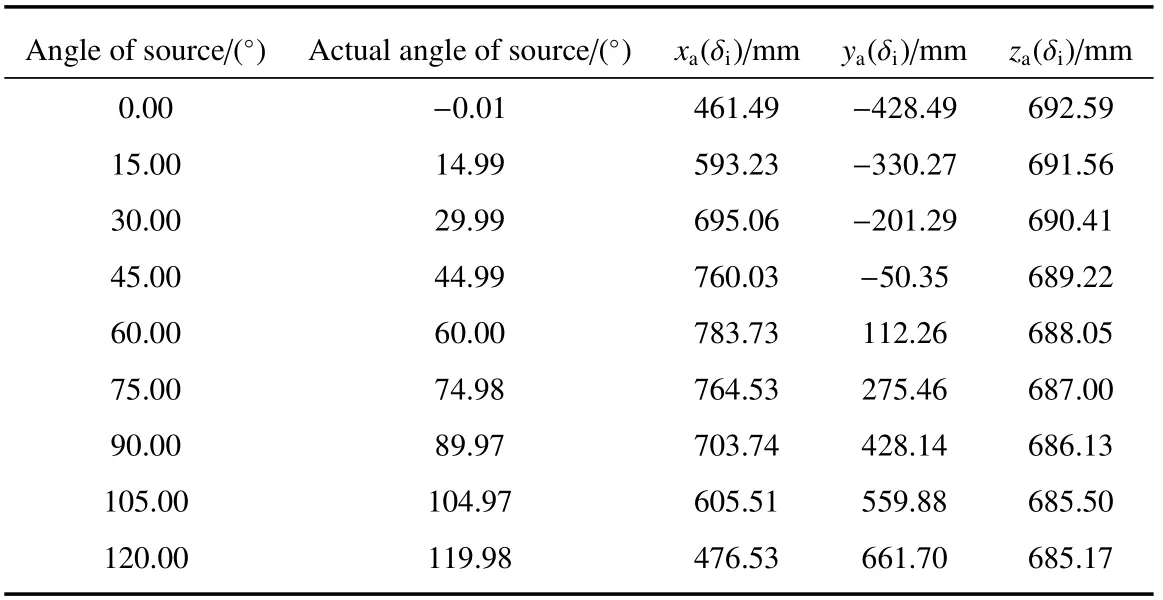
表7 激光束上a点坐标(r=629.5 mm,第二次测试)Table 7 Coordinates of point a on laser beam(r=629.5 mm,The second test)

表8 实验室坐标系原点位置以及与机器人基坐标系变换角度(第二次测试)Table 8 Origin position of the laboratory coordinate system and the transformation angle with the robot base coordinate system(The second test)

3.2 基于镜反射实验结果的验证与讨论

为了验证BRDF测量装置转角的不确定度,设计了基于镜反射的实验,进行了多组角度的测量(天顶角范围为6°～75°,间隔3°,入射方位角范围为0°～320°,相应反射方位角范围为-180°～140°,间隔40°),观察反射光斑中心的位置,结果如图7所示,其中X轴表示反射光斑中心与实验室坐标系YZ平面的距离,Y轴表示反射光斑中心与实验室坐标系XZ平面的距离,各点的天顶角已在图中标出。由图7可见,基于镜反射实验时,同一天顶角不同方位角的反射误差是一致的。当天顶角发生变化,反射误差也会发生变化,最后计算得到BRDF测量装置转角不确定度为0.0495°,优于0.05°。

图7 基于镜反射测量反射光斑位置数据Fig.7 Measurement of reflected spot position data based on mirror reflection

实际上,在测量时工具坐标系原点与激光束对准会存在误差,从而影响标校结果,所以在前面提到任意两条激光束交点在半径为0.2 mm的圆内即认为实际上激光束都交于一点。根据最后标校得到的转角不确定度,可由(22)式计算出光源在入射角为45°时BRDF的相对误差为0.09%,而在较大角度75°时为0.33%,虽然满足应用需求,但仍有降低的空间。

4 结论

BRDF测量装置转角的不确定度是漫反射板等漫反射参照体BRDF绝对测量不确定度的主要来源之一。根据BRDF绝对测量装置的特点,以六轴机器人为测量工具、固定于中空分度盘的积分球光源出射光束作为指示,建立实验室坐标系与机器人基本坐标系之间的变换关系及标校模型,实验结果表明该模型可以有效地进行标校,转角不确定度优于0.05°,进一步降低了BRDF绝对测量的不确定度。同时,基于六轴机器人的标校方法大大简化了装调过程,实现了无接触式标校,为类似装置的标校提供了参考。