用于CO2 捕集的新型石灰煅烧过程的数值分析
2022-10-14张培昆张震威
张培昆,张震威,王 立
北京科技大学能源与环境工程学院,北京 100083
石灰是一种重要的工业原料[1],广泛用于钢铁,烟气脱硫,建筑和造纸等行业[2-4].石灰一般通过在煅烧窑[5-6]中煅烧石灰石而获得,即石灰石受热分解生成石灰和二氧化碳(CO2).石灰石的分解是吸热反应,工业中通常使用化石燃料煅烧石灰石.当前,中国已经是世界上最大的石灰生产国,年产量超2 亿吨,约占世界总产量的70%[7].石灰行业是碳排放的重要来源[6,8],2015 年中国石灰工业的CO2排放量达2.36 亿吨[9].因此,减少我国石灰生产行业的碳排放十分迫切.
石灰煅烧过程发生的化学反应为燃料燃烧以及CaCO3受热分解为CaO 和CO2[10].因此,石灰煅烧过程会产生两部分CO2:(1)石灰石分解过程中释放的CO2(约占石灰石质量的44%)[11];(2)燃料燃烧产生的CO2.其中,第一部分造成的碳排放占主导地位,约占石灰生产总碳排放的70%[6].对于现有常规煅烧工艺,上述两部分CO2混合于燃烧烟气中[12-13].由于烟气中含有大量氮气,捕集CO2需先进行气体分离,从而导致碳捕集成本较高.
为解决该问题,我们提出一种基于CO2循环载气加热的石灰煅烧新工艺,本文的目标是掌握新工艺的煅烧过程特性并对其进行准确设计和有效优化.由于对石灰窑内部进行准确的实验测量非常困难,数学模型已成为对石灰窑进行研究的必不可少的工具,尤其是对于新工艺开发,模拟仿真更是一种经济且有效的研究手段.目前,文献中石灰煅烧窑的数学模型一般为一维稳态模型,即研究各参数沿着石灰窑高度方向上的分布规律.其中,大多数数学模型针对常规竖窑建立.周乃君等[14]对石灰炉炉内过程进行了数值仿真计算与优化,研究了各操作参数对石灰石煅烧过程的影响规律,并据此得到了石灰炉的最优操作条件;Shagapov 等[15]建立了煤烧石灰窑煅烧过程的数学模型,分析得到了不同工况条件下,窑内气固相组分、温度以及质量流量等参数沿着石灰窑高度方向的分布规律;Bes[16]建立了常规竖窑煅烧过程的稳态模型,模型考虑了气固相中的热质传递和化学反应,基于模型计算分析了燃料种类和燃料转化率等工况参数对窑内料块转化率及温度分布的影响规律;Marias 和Bruyères[17]建立了生物质燃料石灰窑煅烧过程的数学模型,并通过工业现场数据验证了模型的正确性;Do 和Specht[18]开发了常规竖窑石灰煅烧过程的数学模型,该模型能够预测窑内温度分布及料块的煅烧行为,可直接用于大型工业立窑的优化和设计;Gutiérrez 和Vandecasteele[19]建立了包含两套微分方程组的竖窑内石灰煅烧过程的数学模型,以确定出口处的气体温度和料块的平均温度,由此对石灰窑进行㶲分析并降低石灰窑的燃料消耗;崔春等[20]应用多孔介质湍流非预混燃烧模型对竖窑内的温度场进行模拟,实现了对某产量为300 t·d-1的气烧石灰环型竖窑内温度场的三维仿真.
相比之下,针对其他类型石灰窑建立的模型较少.Do[21]建立了用于描述常规竖窑和并流蓄热式双膛石灰窑(麦尔兹窑)的数学模型,该模型采用常微分方程组描述了气固相平衡关系,并采用缩核反应模型描述石灰石料块的分解过程;El-Fakharany[22]开发了混烧石灰竖窑的数学模型,分析了不同操作条件对石灰窑操作的影响;Senegacnik 等[23]建立了套筒窑中石灰石料块内传热和煅烧过程的理论模型;刘国辉等[24]为提高产品石灰活性并降低能耗,以产量为200 t·d-1的麦尔兹窑为研究对象,基于Fluent 软件实现了石灰煅烧过程的数值模拟,对比分析了窑内的参数分布.
近年,基于计算流体力学(Computational fluid dynamics,CFD)和离散单元法(Discrete element method,DEM)耦合模拟的方法也被应用于石灰窑的模拟研究.Bluhm-Drenhaus 等[25]建立了石灰生产过程的气固传输耦合模型,基于CFD 建立质量、动量和能量的三维传输模型,同时基于DEM 建立料块的机械运动和分解反应模型;Krause 等[26]提出基于三维料块机理的数学模型,通过耦合三维DEM-CFD 模拟,实现竖窑内石灰石料块的移动和反应过程的模拟;Krause 等[27]还基于Fluent 软件和自制DEM 软件对麦尔兹窑进行了3D-DEMCFD 模拟,研究了窑内燃料燃烧、料块煅烧和热质传递过程.
上述文献为石灰煅烧过程的建模提供了良好的基础,但文献模型不能直接套用于本文研究的石灰煅烧过程,主要原因是新型煅烧过程与常规工艺的煅烧过程存在较大不同,例如反应段气相CO2的分压增加至常规工艺的五倍左右.为此,本文开发了基于CO2加热的石灰煅烧过程数学模型,据此获得各关键参数在煅烧窑中的分布规律,并获得主要工况参数对煅烧过程的影响规律.
1 数学模型
1.1 流程描述
如图1 所示,新工艺采用了新型四段分区的竖窑,通过设置于煅烧窑之外的燃烧加热炉提供热量,并采用CO2作为循环载气将热量带入煅烧窑加热石灰石料块,从而避免了常规煅烧工艺的烟气和CO2(石灰石分解形成的CO2)混合问题;采用空气对石灰进行冷却,从而避免了CO2对石灰的再碳酸化问题.这样一来,无需分离过程即可直接捕集由石灰石分解产生的CO2,从而使石灰生产的碳排放减少约70%.该工艺的石灰冷却过程与常规工艺相同(即空气冷却),其特殊之处是预热段和反应段内的基于CO2加热的新型煅烧过程.

图1 基于CO2 循环载气加热的石灰煅烧工艺Fig.1 Lime calcination process based on CO2 circulating carrier gas heating
1.2 模型简化与假设
本文研究的基于CO2加热的石灰煅烧过程的原理如图2 所示,其中忽略了与常规工艺相同的冷却段以及参数不发生显著变化的均热段,而仅研究与常规工艺不同的预热段和反应段.石灰石料块从煅烧窑顶部装入(进料),经煅烧形成石灰后从底部排出,整个过程中料块在重力的作用下缓慢向下移动.高温的进气(CO2)从煅烧窑底部通入反应段,以提供石灰石受热分解反应所需要的热量,从反应段排出的CO2进入上方的预热段,预热段中料块被上升的CO2以逆流方式预热,并最终从顶部排出尾气(CO2).与常规烟气煅烧模型相比,基于CO2加热的石灰煅烧过程模型主要有以下不同之处:(1)煅烧窑内无需考虑燃料的燃烧;(2)煅烧窑内CO2的分压增加了约五倍,石灰石分解反应的平衡温度提高;(3)煅烧窑内为纯CO2气氛,CO2为发射性气体,因此须考虑辐射换热.
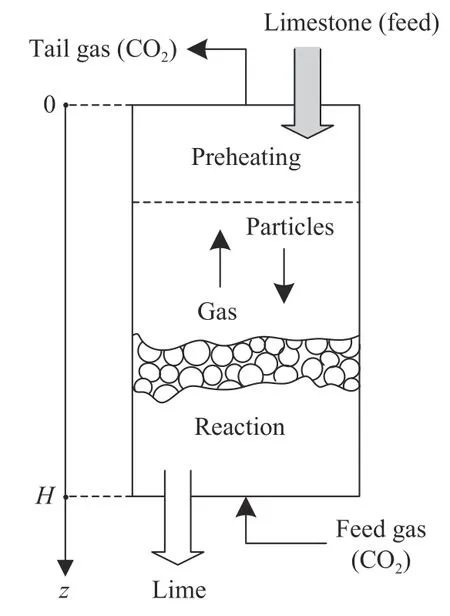
图2 基于CO2 加热的石灰煅烧过程的原理Fig.2 Principle of the lime calcination process using CO2 heating
图2 所示的煅烧过程中,石灰石的热分解行为由三个过程决定:(1)热量从周围的气相传递到料块表面的对流换热过程;(2)热量从表面通过产物层传递至反应界面的导热过程,该过程保证了界面处化学反应的持续推进;(3)反应生成的CO2气体的传质过程,即CO2从反应界面进入产物层,再从产物层扩散至料块表面并最终进入气相.
本文建立的石灰煅烧过程数学模型为一维稳态模型,即假定任何横截面的特性(气体和料块的温度以及料块转化率等)是均匀的,变化仅限于垂直方向,并且料块在煅烧窑内的下降过程是匀速稳定的.为合理简化模型,建模过程还需进行以下假设:(1)料块为球形,且料块在煅烧窑内保持外形及尺寸不变(忽略磨损和烧结等),即料块离开煅烧窑时的形状和大小与进入时相同;(2)料块在煅烧窑中的堆积方式为等径球体的立方体排列;(3)煅烧窑顶部装入的石灰石料块只含CaCO3;(4)石灰石分解反应为缩核反应,即料块中心为未反应的CaCO3核,核外的产物层为CaO 壳;(5)氧化钙壳内的传热方式为热传导,并忽略碳酸钙核的热阻.
1.3 单料块反应控制方程组
图3 示出了石灰石料块分解的缩核反应模型.当料块温度高于分解温度时,石灰石开始反应.由于反应所需的热量来自于料块外部,因此料块表面会首先开始反应,形成反应界面.随着反应进行,反应界面从料块的表面逐渐向中心发展,反应界面外部为壳(CaO),反应界面内部为核(CaCO3).如图3 所示,为了维持反应的持续进行,一方面,外部热量需要经历两个步骤到达反应界面,即气相和料块表面之间的换热,以及从料块表面到反应界面的导热,在反应过程中进入核的热量很少,因此忽略不计;另一方面,反应界面的温度对应着平衡压力,平衡压力和界面压力之差为反应驱动力,反应界面处生成的CO2需要扩散至料块表面并进入气相.
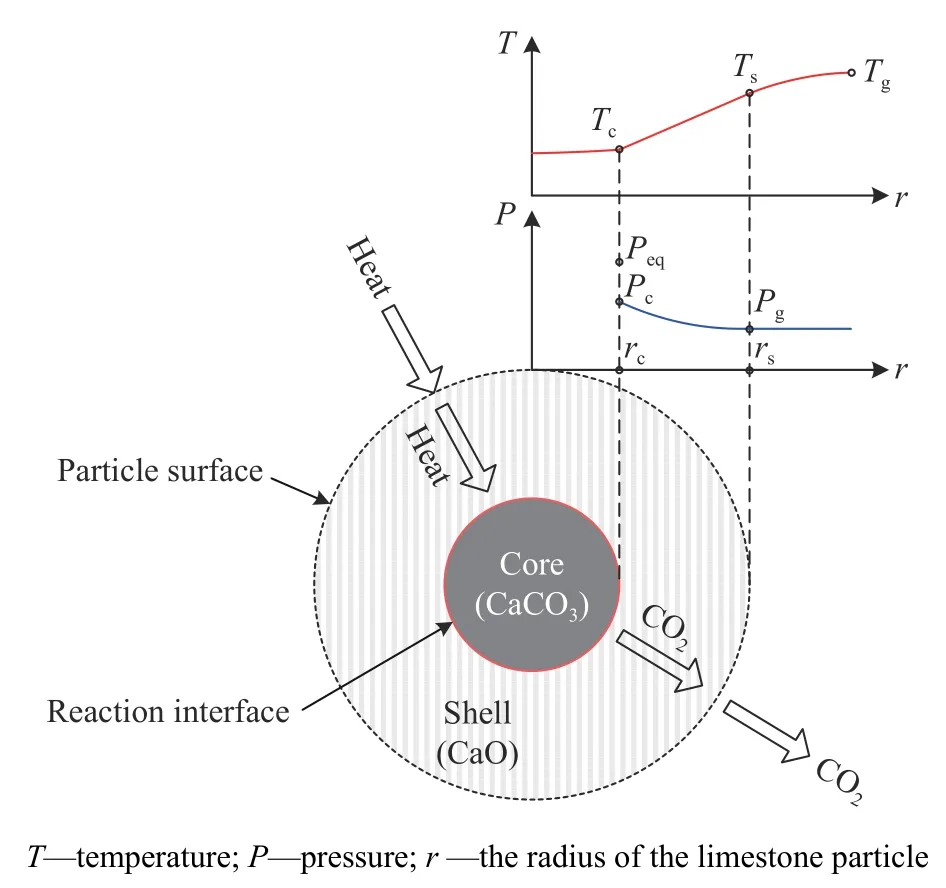
图3 基于CO2 加热的石灰石料块缩核反应模型Fig.3 Shrinkage reaction model of the limestone particle using CO2 heating
基于缩核模型建立的单料块模型如下.单料块中反应界面处CO2的生成量为:
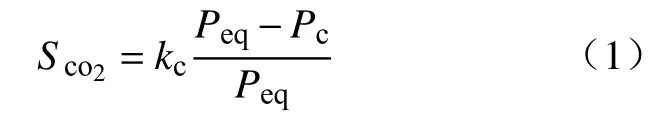

式中,Tc为反应界面温度,K;R为理想气体常数,J·mol-1·K-1.
Peq为反应界面处温度的函数,其计算表达式为:

单料块中CO2向外扩散的传质方程为:

式中,rs为料块半径,m;rc为反应界面半径,m;De为 CO2在壳内的有效扩散系数,m2·s-1;Pg为气相压力,Pa.
单料块的质量守恒方程为:

式中,u为料块在煅烧窑中的下降速度,m·s-1;z为煅烧窑内任一点处的高度,m;ML为石灰石的分子量,kg·mol-1;ρL为石灰石的密度,kg·m-3.
u的计算表达式为:

式中,ε为煅烧窑中料块堆积的空隙率;A为煅烧窑的横截面积,m2;mL为石灰石料块进料的质量流量,kg·s-1.
单料块表面的气-固换热方程为:
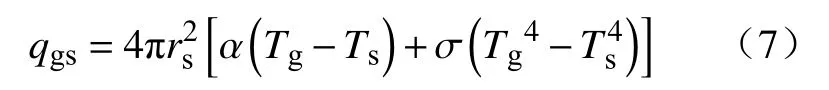
式中,qgs为气-固相换热负荷,kW;Ts为料块表面温度,K;Tg为气相温度,K;α为对流换热系数,kW·m-2·K-1;σ为辐射换热系数,kW·m-2·K-4.
单料块中壳的导热方程为:

式中,qsc为壳内从料块表面向反应界面导热的热负荷,kW ;λQ为壳的热导率,kW·m-1·K-1.
单料块中核的能量守恒方程如式(9)所示(假设条件中忽略核的热阻,因此核内温度分布均匀,均等于Tc):
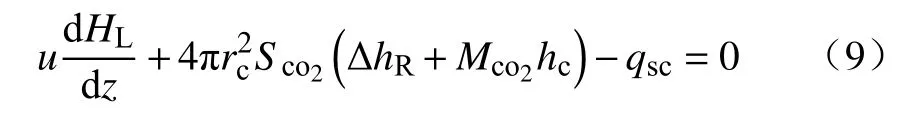
式中,HL为核的总焓,kJ;ΔhR为石灰石分解的反应焓,kJ·mol-1;为CO2的分子量,kg·mol-1;hc为离开反应界面的CO2的比焓,hc=,kJ·kg-1;其中,Cc为 CO2的比热容,kJ·kg-1·K-1;T为温度,K;Tref为参考温度,K.
核的总焓HL的 计算表达式为:

式中,hL为核的比焓,kJ·kg-1;hL=中,CL为核的比热容,kJ·kg-1·K-1.
单料块中壳的能量守恒方程为:
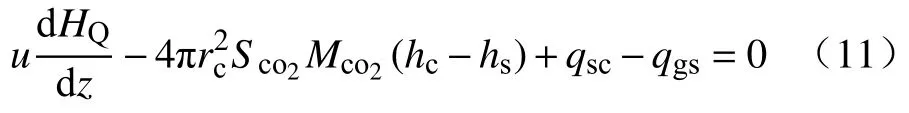
式中,HQ为壳的总焓,kJ;hs为离开料块表面的CO2的比焓,hs=,kJ·kg-1.
由于料块的壳内具有温度梯度,因此HQ需通过进一步假设估算求得.假设从表面到反应界面的温度呈线性分布(Iliuta 等[28]指出壳内的温度接近线性分布),可得HQ表达式如式(12)所示:

式中,ρQ为壳的密度,kg·m-3;CQ为壳的比热容,kJ·kg-1·K-1;r为料块中任一点处的半径,m.
1.4 气相控制方程组
由于气相中气体温度和流量沿着煅烧窑的高度方向是变化的,料块在下降过程中所接触气氛的相关参数会发生改变.因此,为完整描述煅烧过程,使得模型方程闭合,还需围绕气相建立以下平衡关系.
气相的质量守恒方程为:

式中,N为单位高度煅烧窑中的料块数量;mg为气相中气体的质量流量,kg·s-1.其中,N的计算表达式为:

气相的能量守恒方程为:
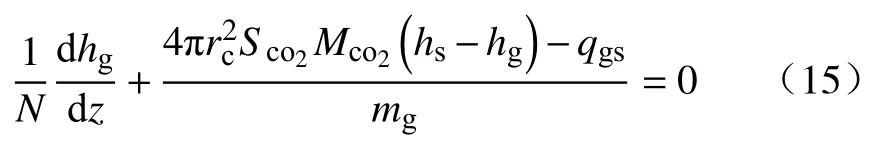
式中,hg为气相中 CO2的比焓,hg=,kJ·kg-1.
1.5 传热系数
单料块表面气-固换热包括对流换热和辐射换热.其中,对流换热系数的计算如下.
单料块表面的努谢尔数由下式计算[29]:

式中,Nu1am为单料块表面的层流努谢尔数;Nuturb为单料块表面的湍流努谢尔数.
Nu1am的计算表达式为:
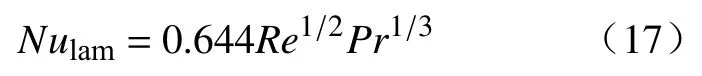
Nuturb的计算表达式为:
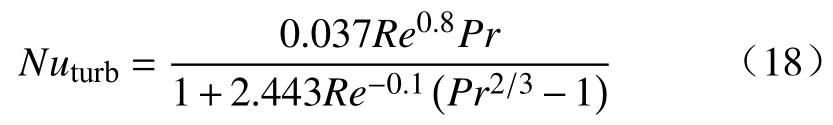
普朗特数的计算表达式为:

式中,µg为料块表面气体的动力黏度,kg·m-1·s-1;λg为料块表面气体的导热系数,kW·m-1·K-1.
雷诺数的计算表达式为:

式中,ρg为料块表面气体的密度,kg·m-3;ug为料块表面气体的流速,m·s-1.ug的计算表达式为:

由此,可得单料块表面气-固对流换热系数:

煅烧窑内气相为纯CO2,CO2为发射性气体,其与料块表面之间的辐射换热和气体空间的大小和形状有关.根据假设条件中规定的料块堆积方式,可求出气体辐射的平均射线行程为L=0.304rs[30].根据平均射线行程,进一步结合CO2压力及温度,通过查CO2发射率数据库获得CO2的发射率.由此,可得单料块表面气-固辐射换热系数:
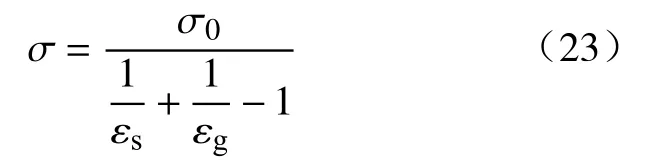
式中,σ0为黑体辐射常数,kW·m-2·K-4;εg为料块表面气体的发射率;εs为料块表面的发射率.
上述模型包含五个常微分方程和若干个代数方程,基于模型方程以及z=0 和z=H处的边界条件,可对模型进行求解.本文采用有限差分法对模型进行离散化,并通过Matlab 语言进行编程求解.
2 结果与分析
本文以一套产量为200 t·d-1的竖窑为案例进行模型计算和分析,该竖窑的主要参数来自于文献[11]中.为便于对煅烧过程进行分析,还需进一步定义转化率、气固温差和节点温差.其中,转化率的计算表达式为:
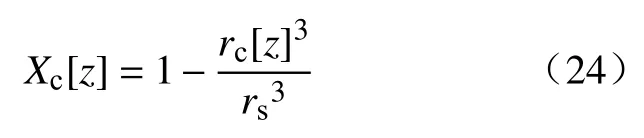
气固温差的计算表达式为:

节点温差的计算表达式为:

首先,对典型工况下的系统进行了计算,模型计算所需的参数和模型的边界条件分别列于表1和表2 中,主要计算结果列于表3,煅烧窑中主要的参数分布展示于图4 中,并通过节点温差确定了预热段和反应段的分界.其次,在典型工况的基础上,改变主要工况参数(进气温度、进气流量和料块半径)分别进行模拟,分析它们对煅烧过程关键性能参数(料块转化率、尾气温度和节点温差)的影响规律.
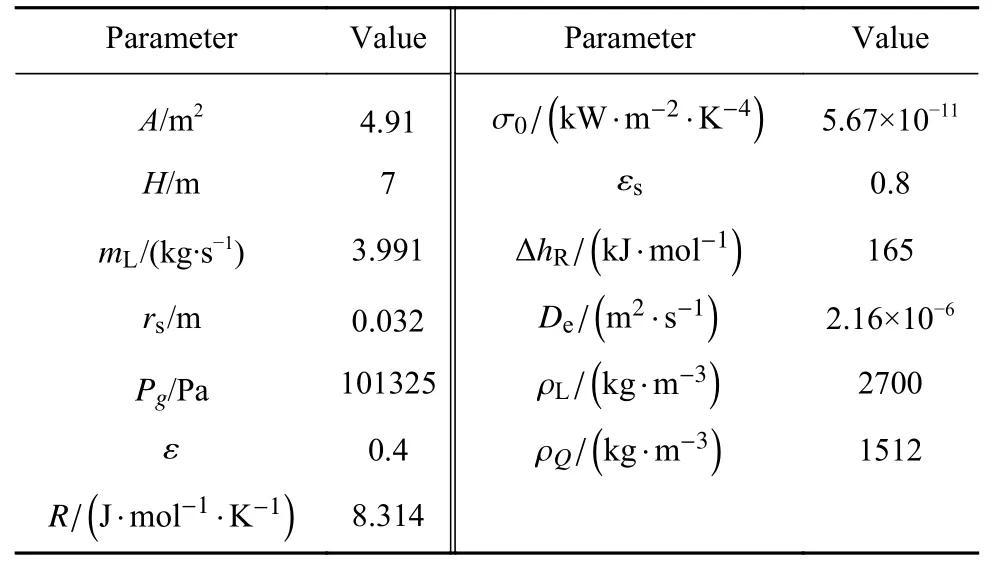
表1 模型计算所需的参数Table 1 Parameters for model calculations

表2 模型的边界条件Table 2 Boundary conditions of the model

表3 模型的主要计算结果Table 3 Major results of model calculations
图4 为典型工况下煅烧窑内的参数分布情况.图4(a)展示了气相温度、料块表面温度、反应界面温度以及气固温差的分布曲线.其中,气固温差曲线存在一个最小值,即节点温差 ΔTp,其所在之处(z=1.35 m)为预热段和反应段的分界;由此可见,煅烧窑的预热段长度为1.35 m,预热段占窑高的20%左右,该比例明显小于常规煅烧窑(常规煅烧窑该比例一般为50%左右[16]),有利于降低整个煅烧窑的高度.在预热段内,在逆流载气的预热下,料块表面温度沿着料块下降方向(窑高z方向)急剧上升,其中窑顶处(z=0)的气固温差最大,且气固温差沿着窑高z方向急剧下降至节点温差;因为尚未发生分解反应,反应界面温度始终等于料块表面温度.在反应段内,在逆流载气的加热下,料块表面温度达到起始反应温度,反应界面形成;料块表面温度和反应界面温度均沿着窑高z方向逐渐升高,但反应界面温度的上升较为缓慢;气固温差沿着窑高z方向逐渐升高,达到一个极值后又逐渐下降.
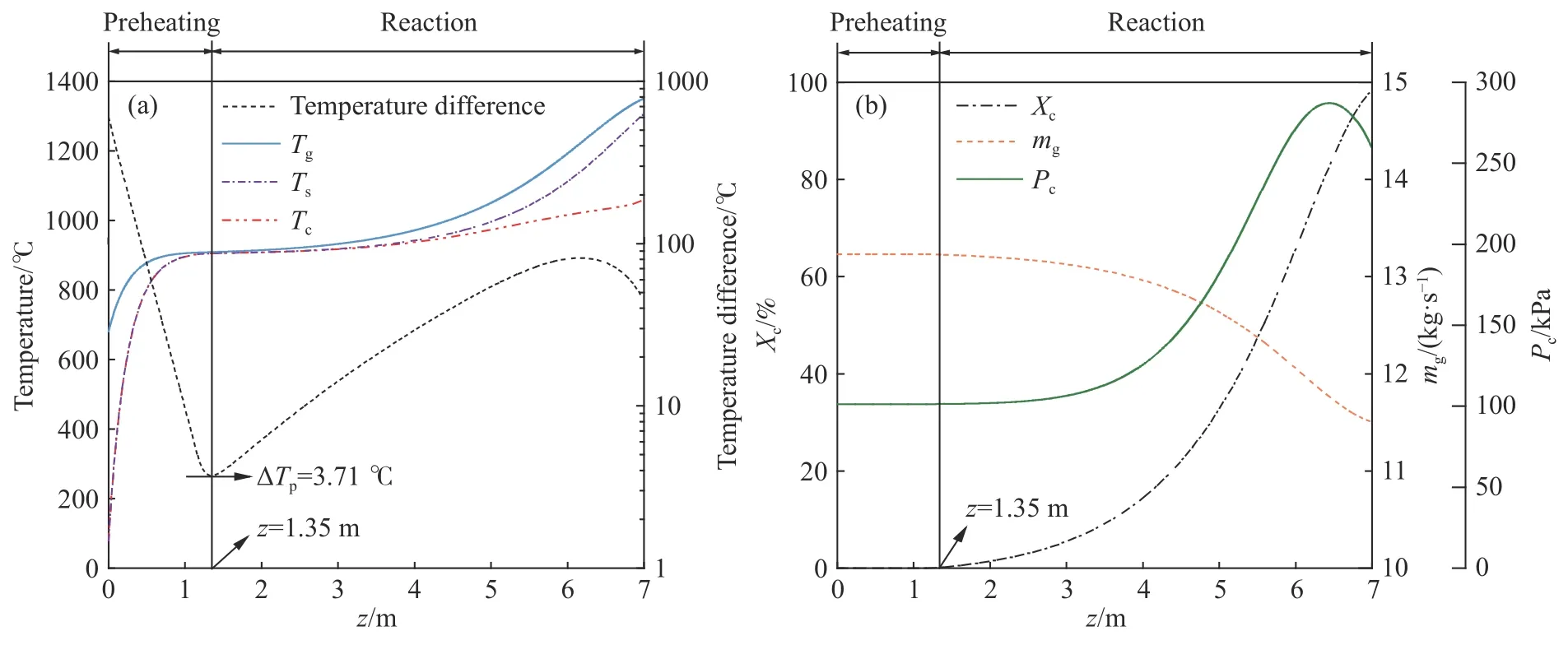
图4 典型工况下的煅烧窑内的参数分布.(a)温度和温差;(b)转化率、气体质量流量和反应界面压力Fig.4 Parameter profiles in the shaft kiln under typical operation conditions: (a) temperature and temperature difference;(b) conversion ratio,mass flow rate of gas,and pressure of reaction interface
图4(b)展示了转化率、气体质量流量和反应界面压力的分布曲线,在预热段内,因为尚未发生分解反应,反应界面压力等于气相压力,所以转化率为零,无反应产物产生,气体质量流量保持恒定.在反应段内,料块开始分解,转化率沿着窑高z方向逐渐升高,料块释放的CO2不断进入气相,气体质量流量沿着载气流动方向逐渐增大;反应界面压力沿着窑高z方向逐渐升高,达到一个极值后又逐渐下降.
2.1 进气温度对煅烧过程的影响
图5 为不同进气温度下煅烧窑内的主要参数分布情况.可以发现,在其他工况参数保持不变的情况下,进气温度的降低对预热段内各参数几乎没有影响,对反应段内的参数分布影响较明显;随着进气温度的降低,反应段内各参数均呈下降态势,且距窑底越近降幅越大,但曲线变化趋势基本保持不变.

图5 不同进气温度下煅烧窑内的主要参数分布.(a)转化率;(b)气体温度;(c)料块表面温度;(d)反应界面温度Fig.5 Profiles of main parameters in the shaft kiln at different feed gas temperatures: (a) conversion ratio;(b) gas temperature;(c) surface temperature of the particle;(d) temperature of the reaction interface
为进一步考察进气温度对煅烧过程的影响,图6 展示了进气温度对煅烧窑关键性能参数的影响规律.可以发现,进气温度越低,最终转化率、节点温差和尾气温度均越低;其中,通过拟合发现,最终转化率和节点温差的变化趋势符合二次多项式规律,尾气温度的变化趋势符合线性规律.

图6 进气温度对关键性能参数的影响规律Fig.6 Influence of the feed gas temperature on key performance parameters
2.2 进气流量对煅烧过程的影响
图7 为不同进气流量下煅烧窑内的主要参数分布情况.可以发现,在其他工况参数保持不变的情况下,进气流量的降低对预热段内各参数有轻微影响,对反应段内的参数分布影响较明显;随着进气流量的降低,反应段内各参数均呈下降态势,且在反应段中部降幅最大,但曲线变化趋势基本保持不变.
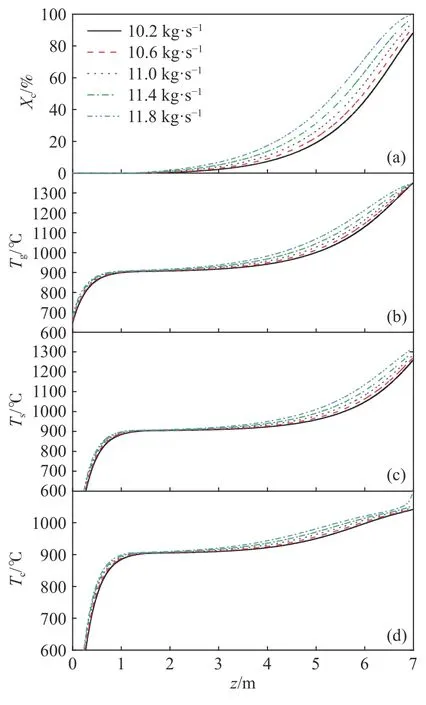
图7 不同进气流量下煅烧窑内的主要参数分布.(a)转化率;(b)气体温度;(c)料块表面温度;(d)反应界面温度Fig.7 Profiles of main parameters in the shaft kiln at different feed gas flow rates: (a) conversion ratio;(b) gas temperature;(c) surface temperature of the particle;(d) temperature of the reaction interface
为进一步考察进气流量对煅烧过程的影响,图8 展示了进气流量对煅烧窑关键性能参数的影响规律.可以发现,进气流量越低,最终转化率、节点温差和尾气温度均越低,且通过拟合发现各参数的变化趋势均符合二次多项式规律.

图8 进气流量对关键性能参数的影响规律Fig.8 Influence of the feed gas flow rate on key performance parameters
2.3 料块半径对煅烧过程的影响
图9 为不同料块半径下煅烧窑内的主要参数分布情况.可以发现,在其他工况参数保持不变的情况下,料块半径的增大对预热段和反应段内的参数分布均有明显的影响;随着料块半径的增大,转化率在反应段内沿着窑高z方向呈先上升后下降的变化趋势;随着料块半径的增大,气相温度在预热段无明显变化,在反应段内沿着窑高z方向呈上升趋势,且在反应段中部的上升幅度最大;随着料块半径的增大,料块表面温度在预热段内沿着窑高z方向呈下降趋势,在反应段内沿着窑高z方向呈上升趋势,且在反应段中部的上升幅度最大;随着料块半径的增大,反应界面温度在预热段内沿着窑高z方向呈下降趋势,在反应段内沿着窑高z方向呈先上升后下降的变化趋势.
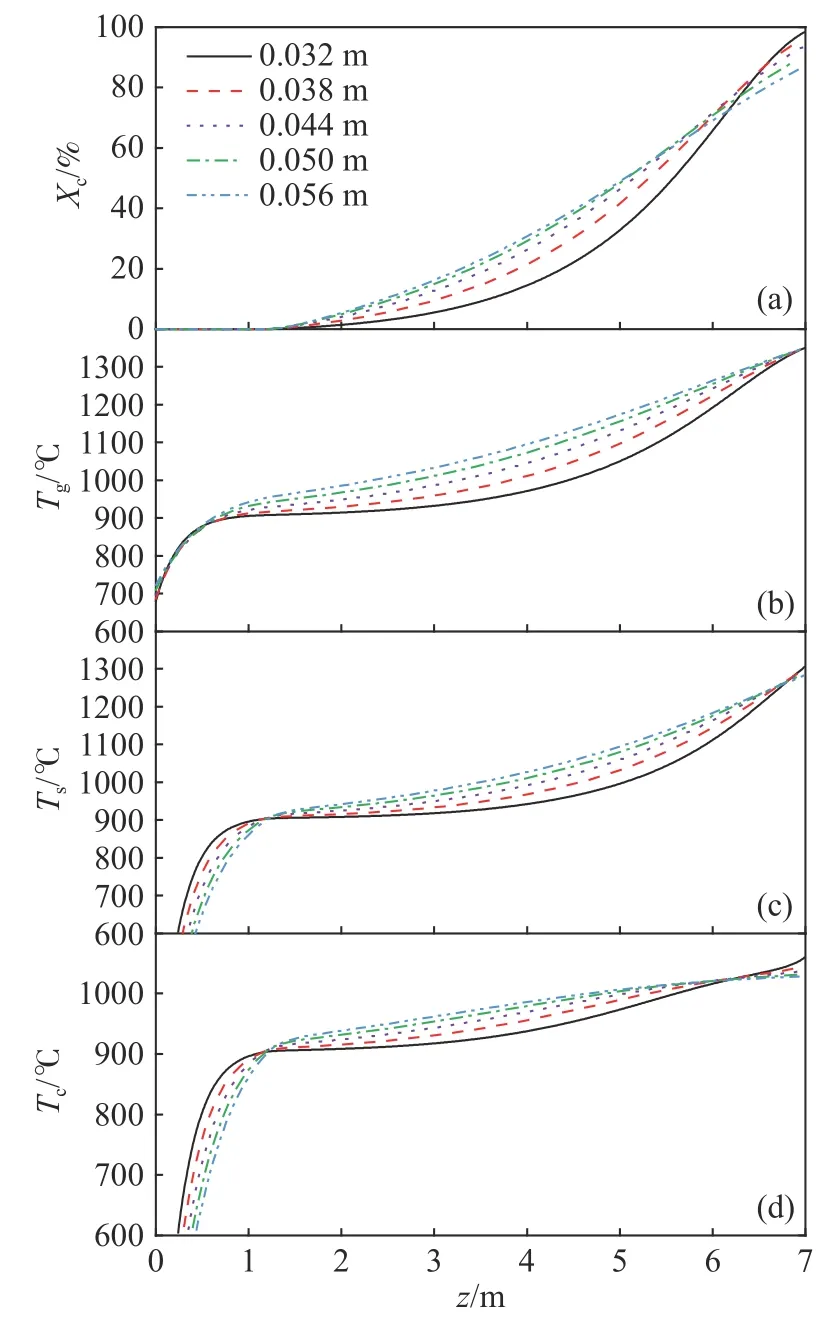
图9 不同料块半径下煅烧窑内的主要参数分布.(a)转化率;(b)气体温度;(c)料块表面温度;(d)反应界面温度Fig.9 Profiles of main parameters in the shaft kiln at different radii of the feeding limestone particle: (a) conversion ratio;(b) gas temperature;(c) surface temperature of the particle;(d) temperature of the reaction interface
为进一步考察料块半径对煅烧过程的影响,图10 展示了料块半径对煅烧窑关键性能参数的影响规律.可以发现,料块半径越大,最终转化率越低,尾气温度越高,节点温差越大;通过拟合发现,各参数的变化趋势均符合三次多项式规律.与进气温度和进气流量相比,在转化率变化幅度相当的情况下,料块半径对节点温差和尾气温度影响幅度较大.
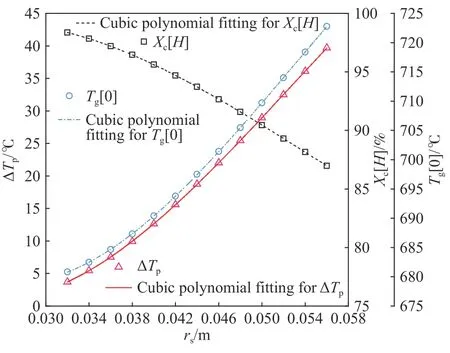
图10 料块半径对关键性能参数的影响规律Fig.10 Influence of the radius of the feeding limestone particle on key performance parameters
3 结论
为掌握基于CO2加热的新型煅烧过程特性并对其进行准确设计和有效优化,本文开发了基于CO2加热的石灰煅烧过程数学模型,并针对案例开展了数值模拟分析.据此,获得了各关键参数在煅烧窑中的分布规律,并通过参数分析阐明了进气温度、进气流量和料块半径对煅烧过程的影响规律,得到以下主要结论:
(1)针对典型工况,通过模拟获得煅烧窑内气固温差最小值(即节点温差)及其位置,确定了预热段和反应段的分界,由此发现预热段占窑高的比例约为20%,该比例显著小于常规煅烧窑.
(2)进气温度和进气流量对预热段内的参数分布无明显影响,但对反应段的影响显著.随着进气温度和进气流量减小,煅烧窑的最终转化率、节点温差均呈非线性(二次多项式规律)降低.
(3)料块半径对预热段和反应段内的参数分布均有显著影响.随着料块半径的增大,煅烧窑的最终转化率呈非线性(三次多项式规律)降低,节点温差呈非线性(三次多项式规律)增加.与进气温度和进气流量相比,在最终转化率变化幅度相当的情况下,料块半径对节点温差影响幅度较大.
