风电机组变桨轴承软带位置及打磨量的分析与研究

李秀珍，陆道辉，钟杰，杨家春

(中车株洲电力机车研究所有限公司风电事业部，湖南株洲 412001)

0 前言

兆瓦级风力发电机组当前都是采用变桨变速的功率控制方式。其中变桨控制是指通过调节叶片的桨矩角来满足风力发电机组的控制要求。通常情况下，当风机运行在额定风速以上时，变桨变速型风力发电机组通过调节叶片的桨矩角[1]52来改变来流的攻角[1]51，从而保持风机输出在额定功率点处。对于更先进的风力发电机组控制方式来说,比如独立变桨控制(IPC)，在风机运行在额定风速以下时，也会对叶片的桨矩角进行及时的微调以达到减小载荷或增加发电量的目的。可以看出，变桨系统的主要功能即是在风机运行中驱动风机叶片旋转以实现变桨，而变桨轴承则是变桨系统中最关键的部件之一。

近年来，随着风电机组功率的增大及叶片长度的增加，变桨轴承故障问题一直层出不穷。因此，对于变桨轴承的深入研究就显得尤为紧迫。但是目前行业内对于变桨轴承的研究主要还是集中在轴承本身的强度、滚道接触角、轴承螺栓孔强度、螺栓强度等方面，而对于变桨轴承软带位置的放置、软带打磨量的设计研究还不够。按照理论设计，软带位置滚珠与滚道之间是不接触的，但是如果将软带放置在载荷较大区域，或者软带打磨的深度不能满足该处的变形量要求，软带区域就会与滚珠接触，产生压力。由于滚道软带位置没有经过热处理，强度和硬度都比滚珠低很多，多次接触后就会导致轴承滚道在软带位置首先出现破坏，进而导致整个轴承滚道的损坏，后果极其严重。因此，研究变桨轴承软带的放置区域、软带位置的打磨量对于变桨轴承的设计、使用甚至风电机组的安全运行都有重要意义。

轴承软带区域指滚道在感应淬火过程中，淬火头的起始点与结束点之间的空白区域。如图1所示，该区域由于未经淬火，滚道的表面强度和硬度均较低，在风机运行过程中需要放置在受力小的位置，且不得与滚子产生接触。

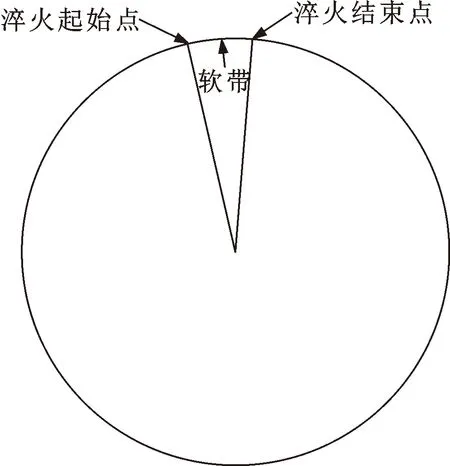
图1 轴承软带示意

1 轴承内外圈相对变形分析

采用非线性弹簧单元模拟滚珠与滚道的力-位移关系，如图2所示。采用O1O3和O2O4在平面内的相对变形量L13和L24代表滚道4个圆弧面的相对变形，并以L13和L24的较大值代表软带处滚子与滚道的接触位移。软带的打磨量不得小于滚珠与滚道的接触相对变形。

图2 非线性弹簧单元

滚动体与每个曲面的接触方式是点接触，如图3所示：2个滚道曲率圆中心的连线与水平线的夹角为接触角α。因此，通过这4个中心点的位移就可以知道接触角的变化。

图3 曲率圆中心及接触角示意

接触变形实际上主要发生在接触区域附近，该模型的建立主要是基于赫兹理论[2]。在赫兹理论中，假定接触区域是一个椭圆，接触应力呈半椭圆函数分布，为计算椭圆尺寸，引入曲率和函数及曲率差函数：

曲率和为

∑ρ=ρI1+ρI2+ρII1+ρII2

曲率差为

式中：Ⅰ表示滚道接触点上排；Ⅱ 表示滚道接触点下排。

对于4点接触球轴承[3]，内圈处的接触应力要大于外圈处的接触应力，所以此处主要确定内圈处的∑ρi和F(ρ)i。

曲率差函数为

接触椭圆区域的长、短半轴分别为

根据Hertz理论，JONES[5]提出了一种确定轴承内外圈相对位移的方法，后来HARRIS和JONES一起对这种方法进行了改进，提出了著名的JHM[6]方法。此方法中对于轴承内外圈相对位移用下式进行计算：

其中:Q为滚子载荷；E为弹性模量；δ*为F(ρ)的函数，其值可以从文献[7]中查得。

非线性弹簧需要定义力和位移的关系，从而达到用非线性弹簧取代滚子的目的。

2 实例计算

2.1 变桨轴承内外圈相对变形计算模型与条件

此次分析基于经典有限元理论[8]，使用三维CAD软件Pro/E建立几何建模，采用ANSYS进行模型的单元划分、材料定义、单元属性设置、接触关系、边界条件和载荷的定义并进行求解。

2.1.1 建立三维模型

采用三维软件Pro/E建立变桨轴承及其周围部件的三维模型，如图4所示。

图4 变桨轴承连接系统

2.1.2 建立有限元模型

根据三维模型建立有限元模型，如图5所示。其中，螺栓连接的部件均采用标准接触，其他部件连接采用绑定接触，叶根中心与叶片假体上端面绑定，叶根载荷通过叶根坐标系施加在叶根中心。边界条件：约束主轴端面和叶根中心点Z向自由度，同时采用旋转对称约束轮毂体的1/3端面。

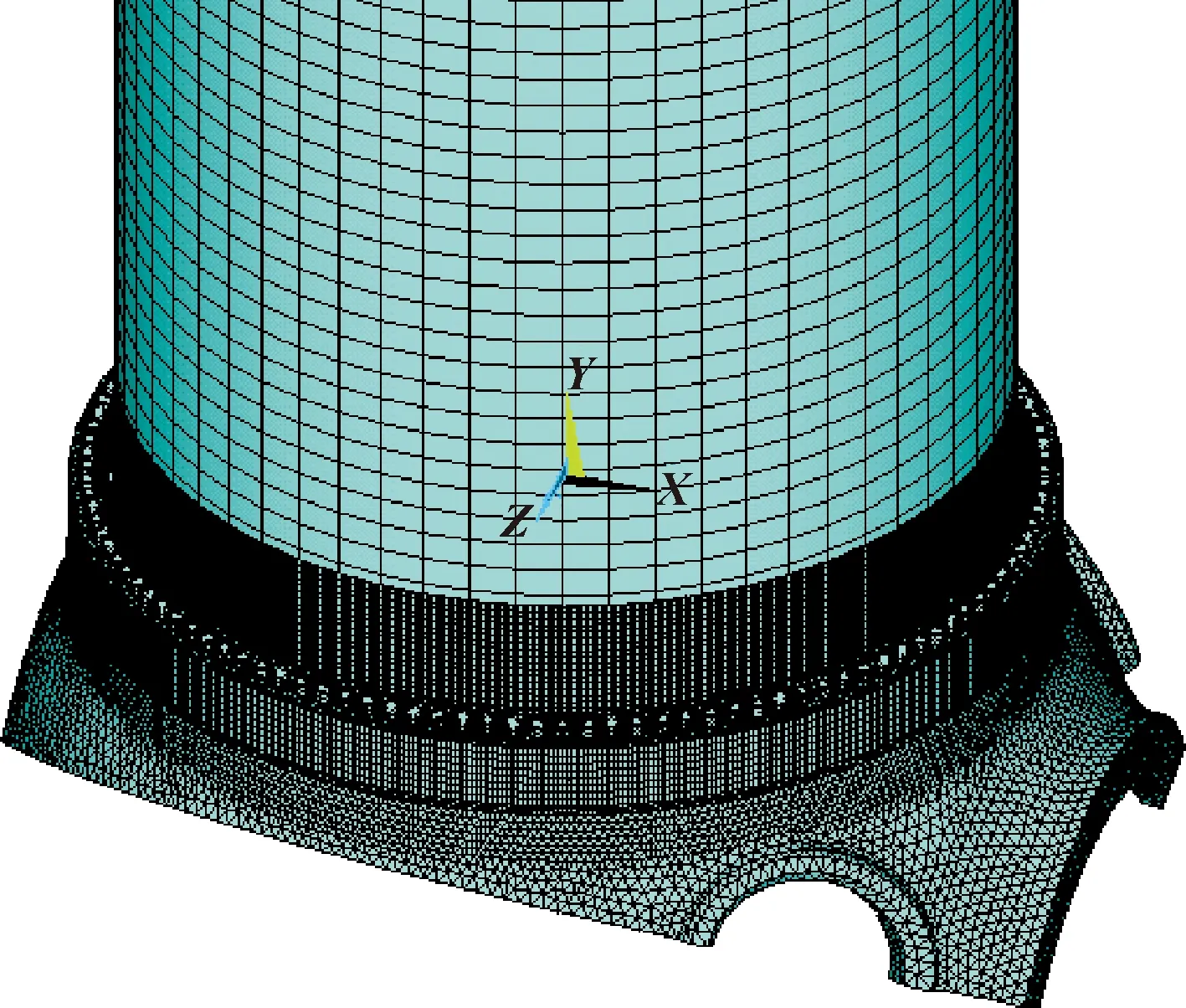
图5 连接系统网格模型

使用Combin39弹簧单元模拟滚子与滚道的接触位移关系，如图6所示。

图6 弹簧单元的力-位移关系曲线

2.1.3 定义材料属性

变桨轴承材料参数见表1。

表1 变桨轴承材料42CrMoA参数

2.1.4 载荷条件

(1)螺栓预紧力

变桨轴承内、外圈螺栓参数及预紧力分别如表2、表3所示。文中采用最小预紧力进行计算。

表2 外圈螺栓参数

表3 内圈螺栓参数

(2)载荷条件

主要针对变桨轴承在极限载荷工况和疲劳载荷工况下，不同角度的相对最大变形量进行对比分析。分别在叶根施加0°、10°、20°、30°、50°、70°、90°、100°、110°、120°、140°、150°、170°等效合弯矩极限载荷和疲劳载荷，载荷采用叶根坐标系，0°和90°方向如图7所示。

图7 0°和90°载荷方向

2.2 计算结果

2.2.1 不同角度、极限载荷下轴承变形量的分析

为便于对数据进行分析，将极限载荷下不同角度滚子-滚道的相对位移值整理成如表4所示。

表4 极限载荷下不同角度滚子-滚道相对位移

由表4可知在极限载荷情况下，滚子-滚道相对位移最大和最小的位置分别为70°、170°，此工况下对应的轴承宏观变形分别如图8、图9所示。

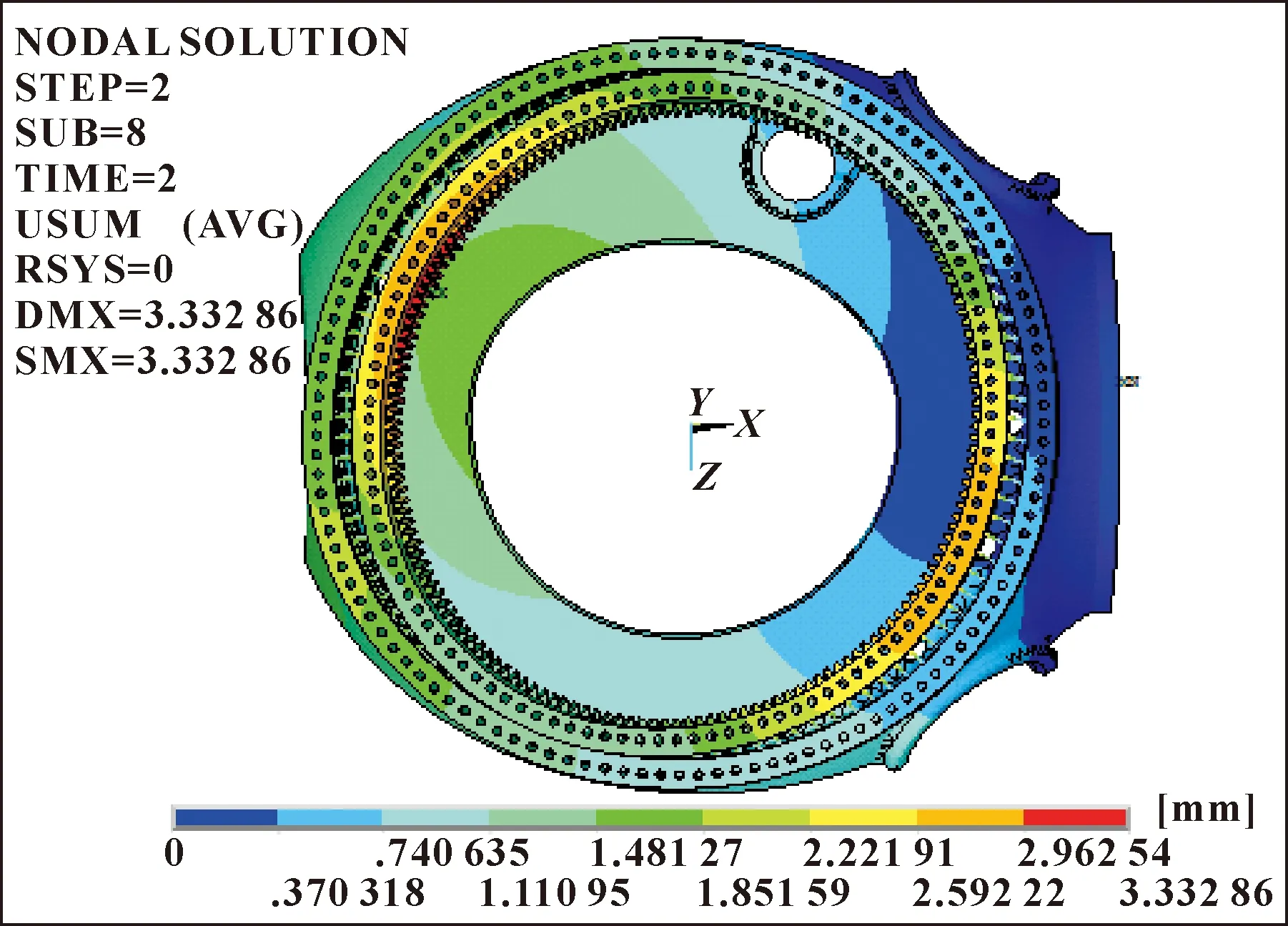
图8 70°载荷方向下轴承变形云图

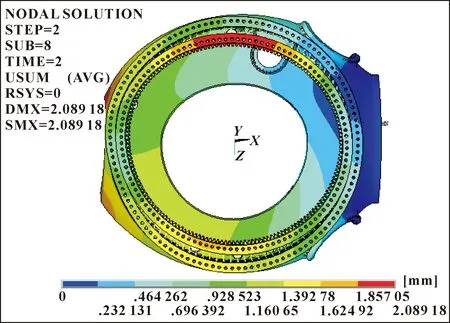
图9 170°载荷方向下轴承变形云图

由表4、图8和图9可知：极限载荷工况下，载荷作用方向为70°时，最大相对位移量为0.336 mm；载荷作用方向为170°时，最大相对位移量为0.187 1 mm。

2.2.2 不同角度、疲劳载荷下轴承变形量的分析

为便于分析数据，将疲劳载荷下不同角度滚子-滚道的相对位移整理成如表5所示。

表5 疲劳载荷下不同角度滚子-滚道相对位移

由表5可知，在疲劳载荷情况下，滚子-滚道相对位移最大和最小的位置分别为20°、110°，此工况下对应的轴承宏观变形如图10、图11所示。

由表5、图10和图11可知：疲劳载荷工况下，载荷作用方向为20°时，最大相对位移为0.261 9 mm；载荷作用方向为110°时，最大相对位移为0.151 8 mm。

图10 20°载荷方向下轴承变形

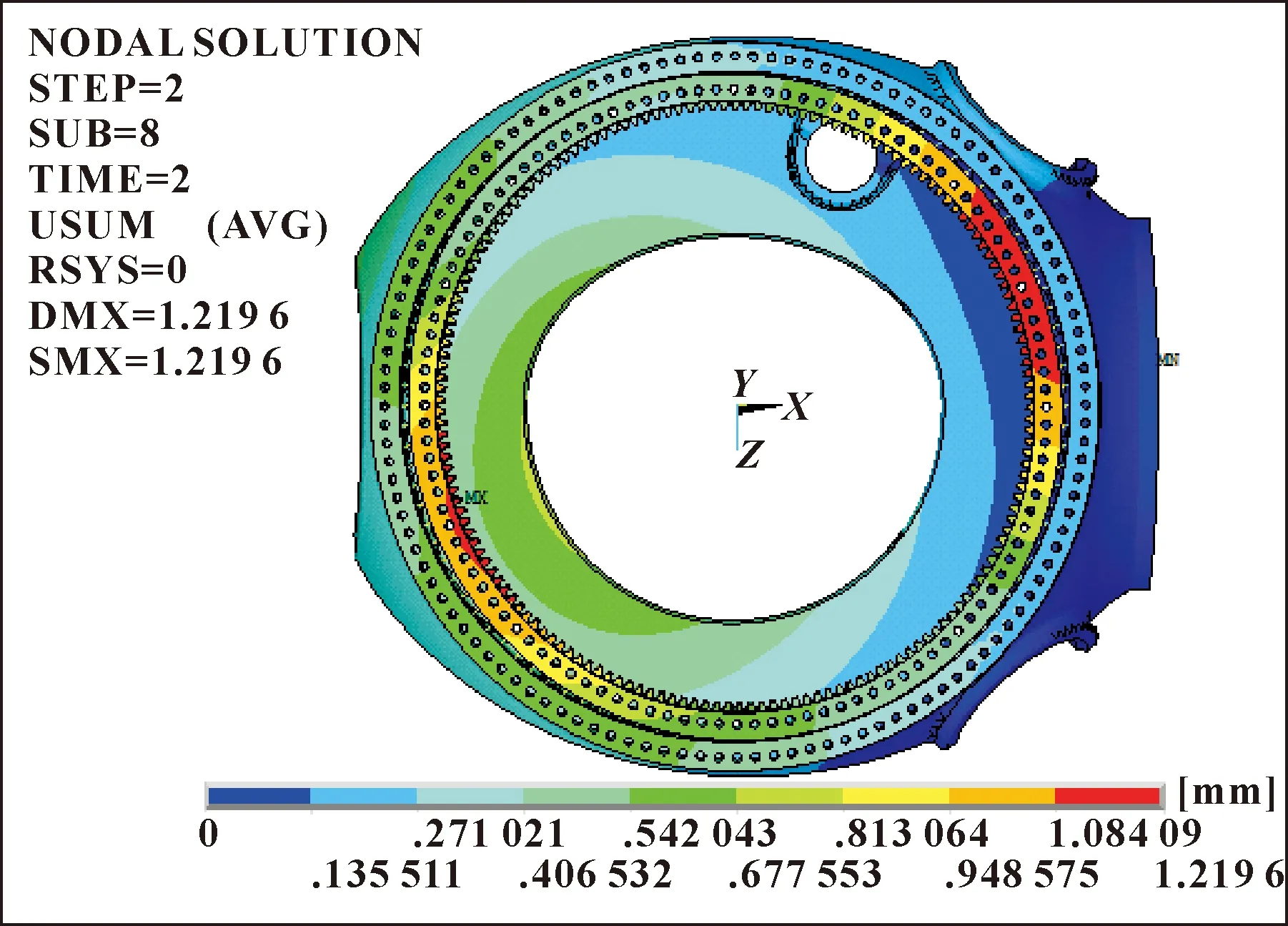
图11 110°载荷方向下轴承变形

2.2.3 不同角度下极限与疲劳变形量的对比分析

不同角度的极限载荷和疲劳载荷工况下的相对位移如图12所示。

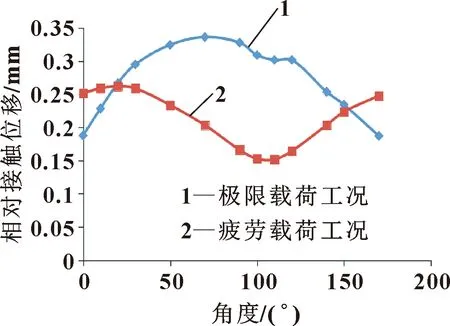
图12 不同角度下极限与疲劳的滚子-滚道相对位移

由图12可知：2条曲线在20°位置和152°位置有交叉，但是152°位置处的相对位移较小。故将软带放在152°位置比较合理，此时极限工况和疲劳工况下的相对变形都较小。

3 结语

(1) 采用有限元方法，分别对极限载荷和疲劳载荷下不同角度的轴承滚子-滚道的相对位移进行仿真分析，得到极限工况下的最大相对位移为0.336 mm、疲劳工况下的最大相对位移为0.261 9 mm。

(2) 找出了所有工况下轴承滚子-滚道相对位移量较小的区域并将极限工况与疲劳工况放在同一条件下进行对比，得到极限工况和疲劳工况下相对位移都比较小的区域为110°～170°；两条曲线在152°位置交叉，说明该点为极限工与疲劳工况下相对位移均较小的点，可将变桨轴承软带放置在该点。

(3)根据计算结果，变桨轴承滚子-滚道的最大相对位移为0.336 mm，因此变桨轴承的软带打磨量建议大于0.336 mm,这样才能确保在风机实际运行过程中，软带位置不会与滚子产生接触。