装配误差下变齿厚渐开线齿轮包络环面蜗杆传动接触分析及试验

2022-10-14陈燕王新华王潇潇

机床与液压 2022年1期

陈燕，王新华，王潇潇

(1.重庆商务职业学院人工智能学院，重庆 401331；2.四川大学空天科学与工程学院，四川成都 610065；3.重庆市商务经济研究院，重庆 401331；4.武汉船舶通信研究所，湖北武汉 430010)

0 前言

蜗杆传动啮合过程中，因共轭齿面加工精度、承受载荷、装配误差、温度变化等原因，导致存在不定边界或可动边界。因此，蜗杆传动的接触问题，是复杂的三维边界不定力学问题[1]。

接触有限元法在齿轮接触问题中应用极其广泛，早在20世纪80、90年代，国内外学者已经开始用有限元法对齿轮或蜗杆传动的齿面接触问题进行研究[2-3]。彭瑞等人[4]探讨了母平面倾角、中心距误差、蜗杆轴向偏移等加工装配误差在单因子情况和综合作用下对鼓形蜗杆接触点的影响规律。王波等人[5]分析了5种工况下，轴交角、中间平面、蜗杆轴向偏移误差等3种安装误差对天线展开机构中蜗杆副齿面接触应力的敏感性。陈东祥和肖延萍[6]研究了3个轴向误差和2个交错角误差下TI蜗杆齿面的接触情况。石万凯等[7]基于有限元弹性接触算法，分析了平面二次包络环面蜗杆传动在制造误差和载荷耦合作用下应力和载荷的齿间分布及接触区域的变化规律。

从上述研究可知，利用接触有限元法分析蜗杆传动在各种误差下齿面的接触直观有效。针对变齿厚渐开线齿轮包络环面蜗杆传动，创建其有限元模型，分析不同载荷及装配误差对齿面应力分布的影响，设计制造传动副样机并考察其接触斑点和传动效率。

1 变齿厚渐开线包络环面蜗杆传动副的有限元模型

仅考虑参与啮合的接触齿对，对变齿厚渐开线齿轮包络环面蜗杆传动副作简化处理，建立其静力学有限元网格模型如图1所示。变齿厚渐开线齿轮材料为20CrMnMo渗碳淬火，弹性模量E1为235 GMPa、泊松比ν1为0.27；环面蜗杆材料为42CrMoA氮化处理，弹性模量E2为212 GMPa、泊松比ν2为0.28。采用正六面体网格，单元数量为27.9万、节点数量为122.5万。

图1 传动副有限元模型

添加的约束条件为：限制环面蜗杆内圈的所有移动和转动自由度，对其内圈添加固定约束；约束变齿厚渐开线齿轮内圈的所有移动自由度和除轴向以外的所有转动自由度，对其内圈添加圆柱约束[8]。将传动副传递的转矩施加在变齿厚渐开线齿轮内圈上，传动副齿面的接触状态如图2所示。

图2 传动副齿面接触状态

2 载荷对齿面应力分布的影响

分析不同载荷下变齿厚渐开线齿轮包络环面蜗杆传动副啮合齿对的接触应力，研究载荷对传动副齿面接触应力的影响及应力沿接触线的分布规律。变齿厚渐开线齿轮和环面蜗杆在250、450、650 N·m等不同载荷下的接触应力分别如图3、图4、图5所示。可以看出：不同载荷下，左齿面等效应力大于右齿面，从齿面应力分布及数值看，右齿面啮合性能好于左齿面；随着载荷的增大，齿面等效应力有所增大，应力分布区域则基本相同，都是沿着接触线分布。

图3 250 N·m载荷下的齿面应力分布

图4 450 N·m载荷下的齿面应力分布

图5 650 N·m载荷下的齿面应力分布

3 装配误差对齿面应力分布的影响

3.1 中心距误差

中心距误差用符号Δfa表示，定义为装配的实际中心距与理论中心距之差，即：

Δfa=ap-at

(1)

式中：ap、at分别为传动副装配的实际中心距和理论中心距。中心距误差如图6所示。

图6 中心距误差示意

对传动副施加450 N·m力矩，后述加载完全相同，不再赘述。分别取中心距误差Δfa为0.1、-0.1 mm，则齿面接触状态分别如图7、图8所示。可以看出：当中心距误差Δfa为0.1 mm时，即增大中心距安装时，齿面接触应力有所增大，齿面应力分布集中在少数齿对，减少了接触线条数，不利于齿面载荷分配，承载能力受限；当中心距误差Δfa为-0.1 mm时，即减少中心距安装时，齿面接触应力明显增大；中心距装配误差对传动副齿面的接触状态影响显著。无论增大中心距还是减少中心距，偏离理论安装位置误差范围时的齿面间均为不正常的啮合状态。

图7 Δfa=0.1 mm时的齿面应力

图8 Δfa=-0.1 mm时的齿面应力

3.2 齿轮轴向偏移误差

齿轮轴向偏移误差用Δfx1表示，定义为齿轮装配的实际轴向中值与理论对中值之差，如图9所示。

图9 齿轮轴向偏移误差

分别取齿轮轴向偏移误差Δfx1为-0.2、0.2 mm，则齿面接触状态分别如图10、图11所示。可以看出：齿轮轴向偏移误差对传动副齿面的接触齿对和接触线条数无影响，但对齿面接触应力略有影响；当齿轮轴向对中偏移误差Δfx1为-0.2 mm时，即实际对中位置往齿轮厚齿端偏移时，应力有所增大，这是由于无侧隙状态下往齿轮厚齿端偏移后产生微量过盈；当齿轮轴向对中偏移误差Δfx1为0.2 mm时，即实际对中位置往齿轮薄齿端偏移时，应力略有减小，这是由无侧隙状态下往齿轮薄齿端偏移后产生间隙导致的。

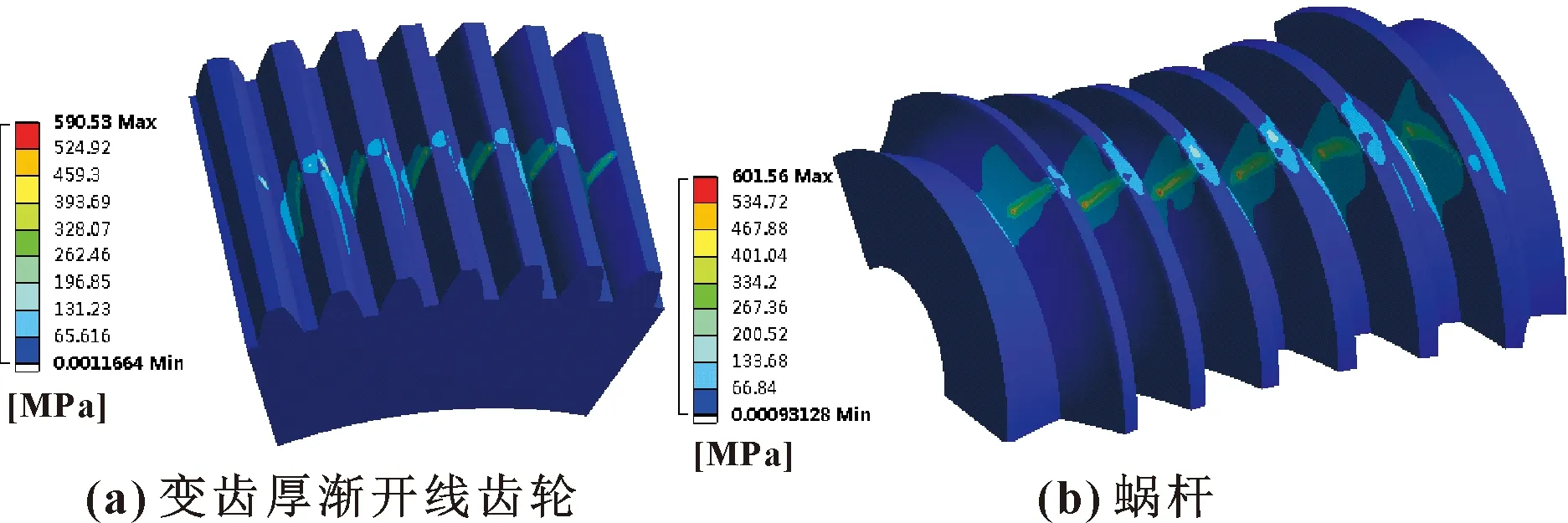
图10 Δfx1=-0.2 mm时的齿面应力状态

图11 Δfx1=0.2 mm时的齿面应力状态

3.3 蜗杆轴向偏移误差

环面蜗杆轴向偏移误差用Δfx2表示，定义为环面蜗杆轴装配的实际轴向中值与理论对中值之差，如图12所示。

图12 环面蜗杆轴向偏移误差

分别取环面蜗杆轴向偏移误差Δfx2为-0.05、0.05 mm，则齿面接触状态分别如图13、图14所示。可以看出：蜗杆轴向偏移误差对传动副齿面的接触齿对和接触线条数无影响，但对齿面接触应力有影响；当蜗杆轴向偏移误差Δfx2为-0.05 mm时，即实际位置往右齿面偏移时，应力增大明显，这是因为右侧齿面螺旋角相对左侧较小，法向误差值相对较大，因此沿蜗杆轴负向的偏移误差对齿面应力影响较大；当蜗杆轴向偏移误差Δfx2为0.05 mm时，即实际位置往左齿面偏移时，齿面接触应力略有增大，这是因为左侧齿面螺旋角相对右侧较大，法向误差相对较小，因此沿蜗杆轴正向的偏移误差对齿面应力影响较小。

图13 Δfx2=-0.05 mm时的齿面应力状态

图14 Δfx2=0.05 mm时的齿面应力状态

3.4 轴交角误差

轴交角误差用Δfθ表示，定义为环面蜗杆轴向与齿轮轴向装配的实际轴交角与理论轴交角之差，即：

Δfθ=θp-θt

(2)

式中：θp为装配的实际轴交角；θt为理论轴交角。轴交角误差示意如图15所示。

图15 轴交角误差示意

分别取轴交角误差Δfθ为-0.2°和0.2°，则齿面接触状态分别如图16、图17所示。可以看出：轴交角误差对传动副齿面的接触齿对和接触线条数几乎无影响，但对齿面接触应力影响非常明显；当轴交角误差Δfθ为-0.2°时，应力显著增大；当轴交角误差Δfθ为0.2°时，齿面应力有所变大，齿面应力分布全齿面。

图16 Δfθ=-0.2°时的齿面应力状态

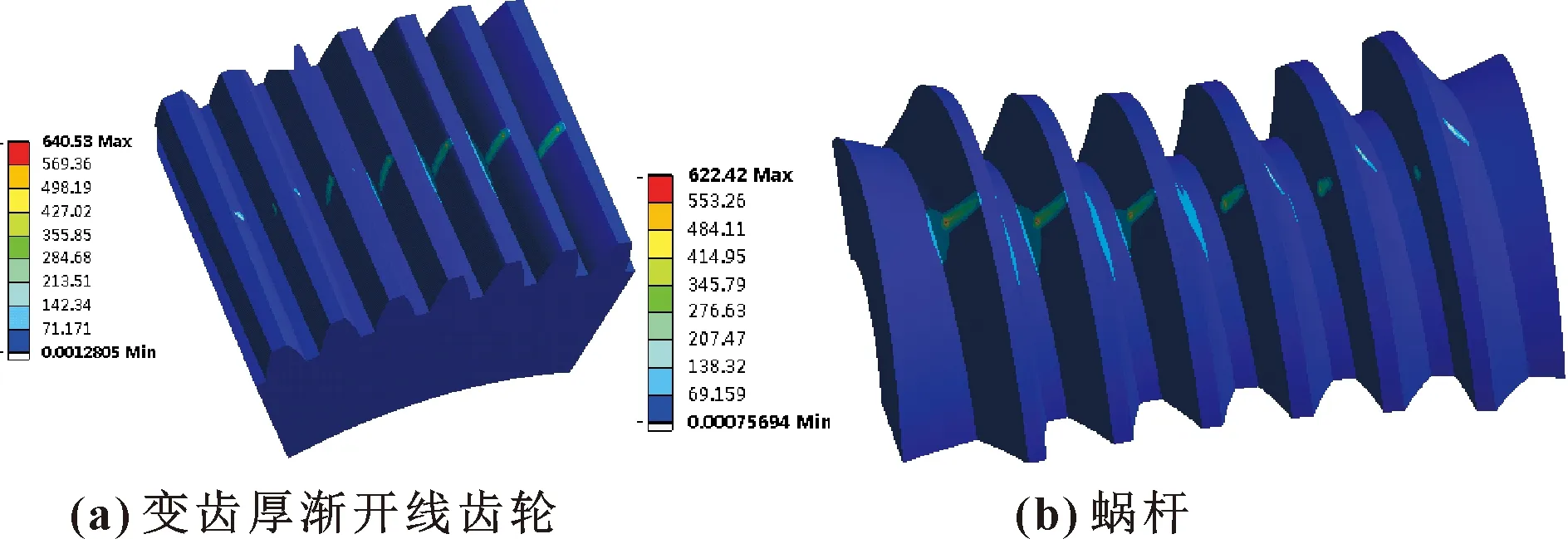
图17 Δfθ=0.2°时的齿面应力状态

4 传动副样机性能试验

根据JB/T 5558—2015中的蜗杆减速器加载方法[9]，搭建试验台。试验台的布置原理如图18所示。通过软件控制电控柜，调节驱动电机和负载电机，两套转矩转速传感器分别与减速器样机的蜗杆轴和蜗轮轴相连，以测定经样机减速前和减速后的转矩和转速；经CatmanEasy数据采集仪采集数据并进行分析处理。

图18 样机性能测试原理

在负载性能试验之前，先进行空载试验，即负载电机不启动，驱动电机逐步加速到1 500 r/min，正反转运行1 h，以确保紧固件无松动、系统运行平稳、无异常噪声、无漏油。而后驱动电机保持转速1 500 r/min，负载电机以50 N·m为步长进行梯度加载，每一梯度运行1 h以上且油池油温平衡后再进行下一梯度运行。传动性能试验如图19所示。