永磁磁阻双转子混合电机的优化设计

孔晓光， 徐 鸿

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

近年来，具有高转矩密度、高效率的双转子永磁同步电机得到了广泛应用.按照磁通方向分类，双转子永磁同步电机一般可以分为轴向磁通双转子永磁同步电机和径向磁通双转子永磁同步电机.其中径向磁通双转子永磁同步电机又分为多种结构[1]，在这些结构中研究较多的是一种具有中间定子、内外双转子的结构.Li等[2]提出了一种新型的永磁磁阻双转子混合电机，图1是利用有限元软件对该永磁磁阻双转子混合电机进行的二维模型建模.直观来看，它与双转子永磁同步电机有着相似结构，两者的异处在于内转子的不同.永磁磁阻双转子混合电机由磁阻转子与定子内侧绕组组成的内电机和表面式永磁转子与定子外侧绕组组成的外电机两部分构成.与双转子永磁同步电机相比，永磁磁阻双转子混合电机用同步磁阻转子代替了内部的表面式永磁转子，避免了内部定子侧绕组产生的热量和永磁体的涡流损耗对内转子上的永磁体造成的性能影响；同时，当电机以高转速运行时，磁阻转子的一体化结构显然具有更好的机械强度.参考文献[2]中还验证了采用铁氧体为永磁材料时，磁阻转子的转矩密度优于内部的表面式永磁转子.由此看来，相比于与其结构类似的双转子永磁同步电机，永磁磁阻双转子混合电机确实有着突出的优点.但永磁磁阻双转子混合电机外部的表面式永磁转子的转矩脉动较大，是内部磁阻转子的转矩脉动的2倍.

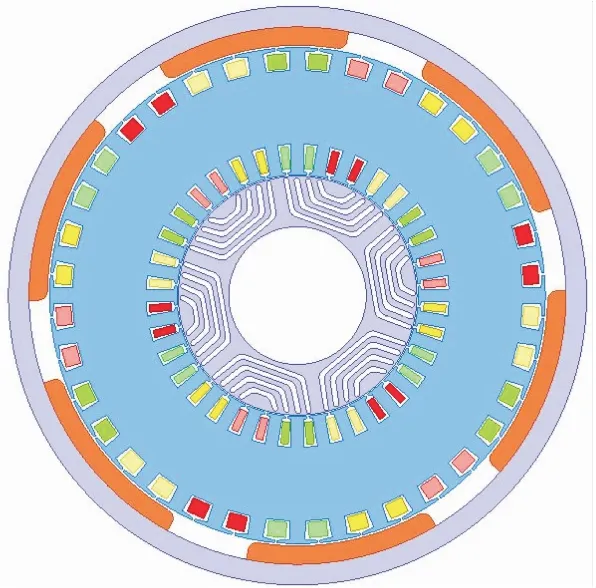
图1 永磁磁阻双转子混合电机的二维结构[2]Fig.1 Two-dimensional structure of permanent magnet reluctance double rotor hybrid motor

程等[3]对电机进行了效率优化，提出优化方法存在两种形式：一是采用一定的控制策略和通过后期的仿真分析进行优化；二是在电机的设计之初就对参数进行优化.如今优化设计方法也从传统的对单一变量进行优化分析来求取最值的局部优化算法变成了现在的各种新型优化方法.新型优化方法是人们借鉴自然社会现象所得，如应用广泛的遗传算法、粒子群算法等全局优化设计算法[4-5]，这类算法的特点是所有的不确定因素都被纳入优化目标之中，但同时计算时间因目标函数建立的复杂性也变长很多.笔者采用一种多目标优化算法(即田口法)对电机的原始参数进行优化来提高电机的转矩性能.

田口法起源于日本以田口玄一为首的一批研究人员开发的正交试验技术，从组合数学理论中的正交拉丁方发展而来，该方法将质量管理与经济效益联系在一起，是一种有效的稳健性设计方法.田口理论认为产品的目标特性与影响目标特性的参数水平组合之间为非线性关系，充分利用各参数的组合与调整能得到较稳定的质量特性[6-7].陈等[8]利用田口法对一种低速大转矩永磁同步电机的性能进行了多变量多目标优化改善.田口法提倡通过优化产品的源头设计来提高产品质量，而不是通过后期的检验.将这种方法应用于电机设计中就是通过优化电机的原始参数提高电机的性能.

实际上，双转子电机中的参数较多，拥有很广的优化空间.笔者利用田口实验方法对永磁磁阻双转子混合电机的原始参数进行优化，以期改善电机的转矩脉动较高的问题和提高电机的输出转矩.以永磁磁阻双转子混合电机的转矩性能为优化目标，合理选择参数作为优化因子，然后从各个优化因子的取值范围中选出一组最优的参数组合，通过比较优化前后的电机性能，验证该优化方法的有效性，提高电机的转矩性能.

1 电机的多目标优化

田口正交实验设计的基本步骤如下：

(1) 确定优化目标，选择优化因子并合理选取因子水平.

(2) 建立正交实验矩阵.正交矩阵形式为Ln(tq),其中:L为正交表的代号；n为正交表的行数；t为水平数；q为正交表中的列数.

(3) 基于有限元模型求解正交矩阵的实验结果.

(4) 对实验结果进行分析，寻找参数的最优值并进行验证.

1.1 优化目标与优化因子的确定

主要针对永磁磁阻双转子混合电机的转矩性能进行优化，包括减小外转子的转矩脉动，以及增大磁阻转子的转矩等，表1为永磁磁阻双转子混合电机的主要参数.在外电机中，永磁体和有槽电枢铁心相互作用，产生齿槽转矩，导致转矩波动，引起振动和噪声.为提高电机输出转矩的平稳性，需降低齿槽转矩.考虑到影响转矩脉动的原因有很多，故将齿槽转矩和转矩脉动一并作为优化目标.设置外转子转矩为优化目标的目的为观测参数变化对外转子转矩的影响.因此，选取以下4个优化目标：齿槽转矩Tc、转矩脉动Tr(外转子)、内转子转矩Ta和外转子转矩Tb.

表1 永磁磁阻双转子混合电机的主要参数Table 1 Main parameters of permanent magnet reluctance double rotor hybrid motor

永磁电机的齿槽转矩削弱方法可归纳为三大类,即改变永磁磁极参数、改变电枢参数以及电枢槽数和极数的合理配合[9].在外电机中除了磁极的极弧系数和外定子槽宽外，同时选取磁极的厚度和外气隙长度也作为优化因子.在电机轴向长度确定的情况下，极弧系数和磁极厚度的变化决定了永磁体的用量.当磁极厚度过小时，永磁体的抗去磁能力会降低.对于气隙长度，值越小也就意味着在外转子中产生同样大小的磁场所需的永磁体也就越少，但是过小的气隙长度会增加电机制造的难度.

即使不考虑磁障结构的改变，内电机采用的磁阻转子的可优化参数也较多[10].磁阻转子内部诸多参数的加入将会造成优化因子的总数增加，正交矩阵的行数即实验次数随之大大增加.其实就一般的相同水平的正交矩阵而言，当水平数t为3时，列数不同的正交矩阵表达式，如L9(34)、L18(37)、L27(313)，增加参数数量将会使正交矩阵的行数增加；而当正交矩阵的列数为一个定值(如7)时，不同水平数的正交矩阵表达式，如L8(27)、L18(37)、L32(47)，实验次数同样会随水平数增加而增加.而田口法追求的是运用最少的实验次数探索出多目标设计的最佳参数组合，所以决定在内电机中仅选取内定子槽口宽度和内气隙长度两个参数作为优化因子，而认为对于内转子的优化应该作为另外一个独立的实验单独进行.

此外，在这种中间定子的永磁磁阻双转子混合电机中，定子轭部厚度h将会影响内外磁场的耦合程度.主要通过改变内、外定子槽的径向长度间接改变定子轭部的厚度，确保电机大小不变，同时h的取值要满足定子的机械强度要求.

在已知初始优化因子水平数的数值情况下选择一个合理的优化因子水平数的取值区间，即首先根据电机设计的经验确定相关参数的一个初始值，然后根据经验在初始值附近指定一个该参数的取值范围作为优化的范围.

内气隙和外气隙的长度的初始值分别是0.3 mm和0.5 mm.它们的取值考虑到了电机的机械可靠性和加工装配误差，同时气隙长度的数值和定子的内径、轴的直径以及电机的极数[11]也有一定的关系.内、外定子槽宽的初始值都为0.4 mm，槽宽的选择主要影响到齿槽转矩的大小.极弧系数的选择考虑到永磁体的利用率和齿槽转矩的大小.定子轭部厚度初始值为11 mm.

选定的7个优化因子如表2所示，这里将每个优化因子的水平数取为3，表2中的水平1、水平2、水平3代表每个优化因子的3个不同的取值.

表2 混合电机的优化因子在不同水平数下的取值Table 2 The value of optimization factor of hybrid motor under different levels

1.2 实验矩阵及数据分析

根据田口法实验设计原理确定正交矩阵形式为L18(37)，即实验次数为18次.正交表具有两条性质：(1) 每一列中，不同的数字出现的次数相等；(2) 任意两列中数字的排列方式均衡.在满足这两条性质情况下得到的正交实验表如表3所示，表中第1列的序号1～18代表共有18组实验，第2列到第8列中的数字1～3代表表2中的各个优化因子的水平数.

利用有限元分析软件对表3中的18个实验一一进行二维模型的建立和模拟仿真，转矩脉动Tr按照公式(1)进行计算[12]，有限元求解的结果如表4所示.

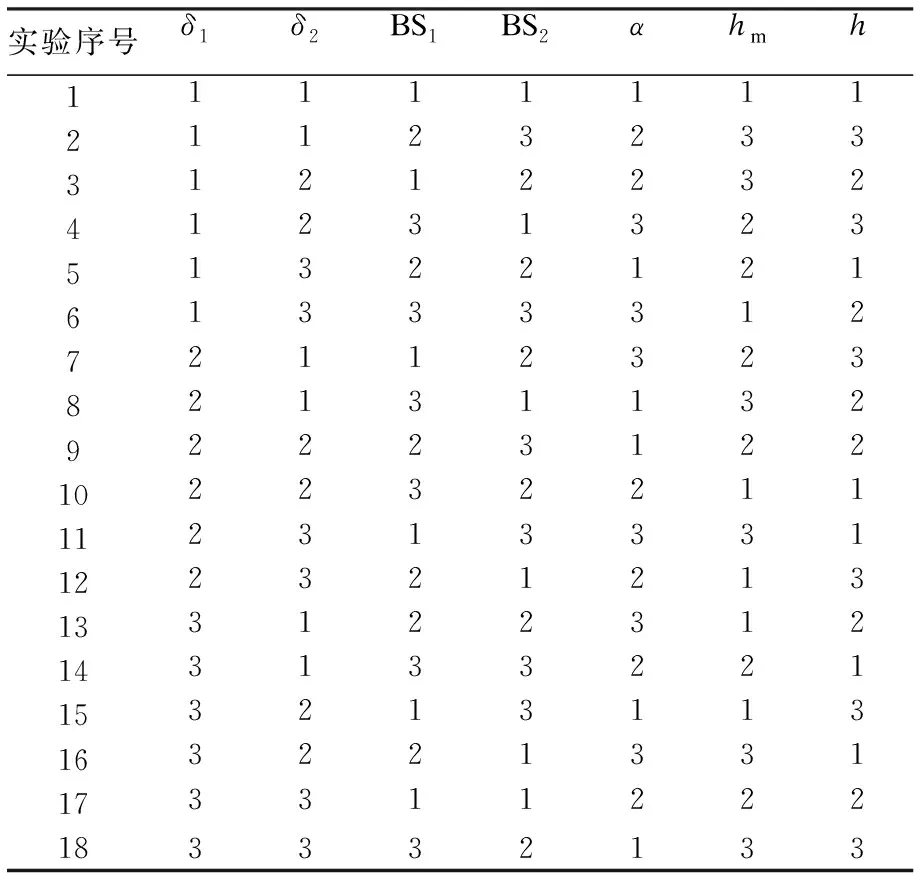
表3 正交实验表Table 3 Orthogonal test table

表4 正交实验结果Table 4 Results of orthogonal experiment

(1)

其中：Tmax为转矩曲线趋于稳定后的最大瞬时转矩；Tmin为最小瞬时转矩；Tav为平均转矩.

要确定各个优化因子对优化目标的影响大小，就要对表4的结果进行平均值分析和方差分析来得到一组最优参数组合.首先根据公式(2)计算表4中各个优化目标的实验结果的平均值，结果如表5所示.

表5 各优化目标实验结果平均值Table 5 Average of experimental results of each optimization target

(2)

其中：m表示优化目标T的平均值；n为实验次数；T表示4个优化目标中的某一个；Ti为优化目标T的第i次实验结果.

由表3知每个优化因子对应的每个水平数下有6个实验结果(即对应每个优化因子的列，数字1～3出现的次数都是6)，而每个因子有3个水平数.利用表3和表4计算各个优化目标的3个水平数下各自的实验结果的平均值(6个实验结果的平均值)，得到各个优化因子变化时各个优化目标的实验结果的平均值如表6所示.

如Tr在BS2的水平数为1下的平均值计算为

Tr(12)+Tr(16)+Tr(17)].

(3)

由表3可知优化因子BS2的水平数1只存在于实验1、4、8、12、16和17中.表6中的所有数据可以依照公式(3)类似得出.

表6 各优化目标在各个优化因子的各个 水平数下的平均值Table 6 Average values of optimization objectives at each level of each optimization factor

将表6中的数据用图更直观地表示，如图2所示.

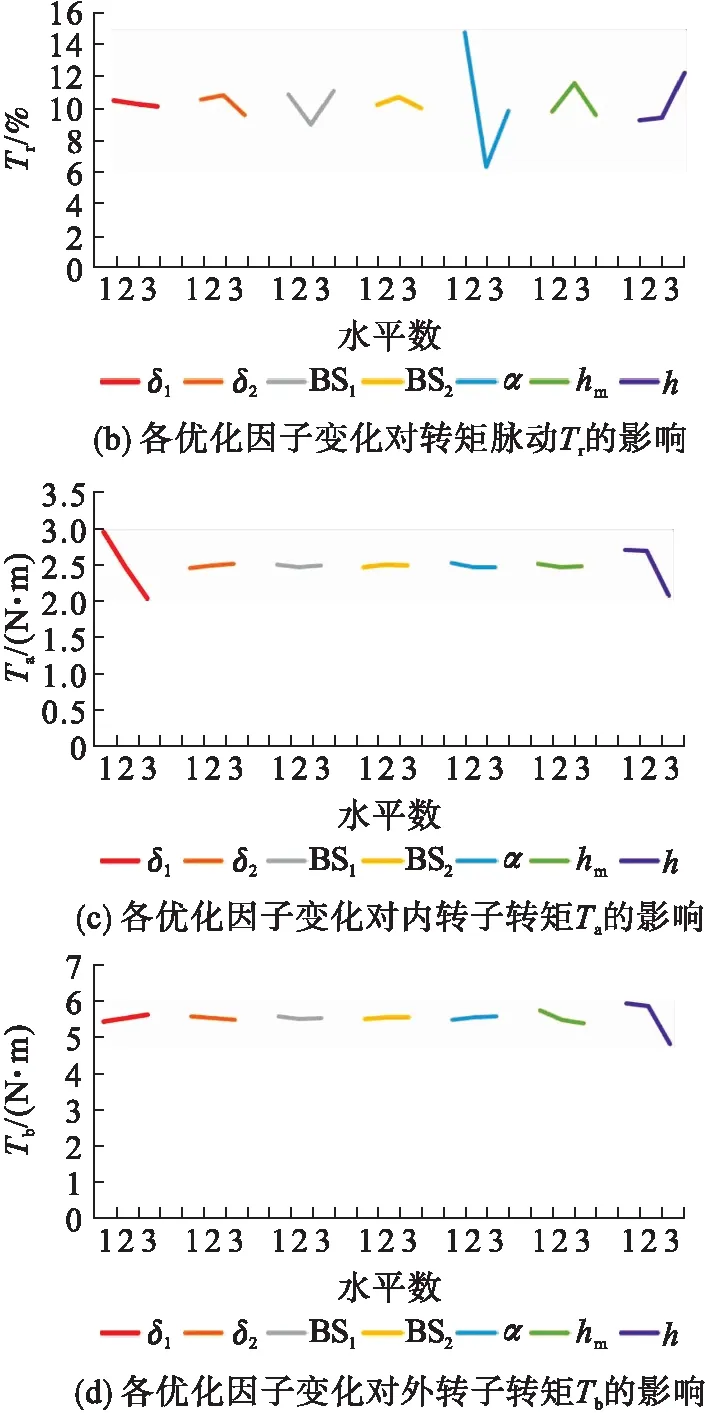
图2 各优化因子变化对Tc、Tr、Ta、Tb的影响Fig.2 Effects of changes in optimization factors on Tc,Tr,Ta and Tb

分析图2可以发现7个参数对Tc、Tr、Ta、Tb的影响程度是不同的，这一点可以从各优化因子的3个水平对应的实验结果的曲线变化坡度可以看出.所以，虽然可以轻易得出使某个优化目标达到最佳效果的各优化因子组合(这样的结果可以得出4组)，但很显然这4个组合不可能相同.例如在所取参数水平范围内要追求最小Tc值时会取h的水平数为3，但此时h的取值却使转矩脉动Tr最大，这源于单个参数对于不同优化目标的影响方式不同，不同曲线的坡度的差异预示了其影响程度也不同.

在对整个电机进行优化时，单纯的单目标优化显然不能满足需求.在这种情况下，必须知道各优化因子对于各优化目标的影响程度，然后按照影响程度选取各因子水平数，最后形成一组最佳的优化因子组合，这便是方差分析.

在方差分析中，组间离差平方和SS反映了各组样本(上文中对于某个参数的不同水平数下的优化目标的值)之间的差异程度，即由变异因素的水平不同(上文中优化因子的水平数1～3)所引起的系统误差.利用表5和表6中的数据计算可得到优化因子对各优化目标的影响所占的比重，SS的计算公式为

(4)

式中：n为各个因子的水平数；m代表某个优化目标的平均值；i指的是水平数；mi为表6中对应优化目标m的水平数为i的值.表7为计算得到的各优化因子对Tc、Tr、Ta、Tb的影响比重.

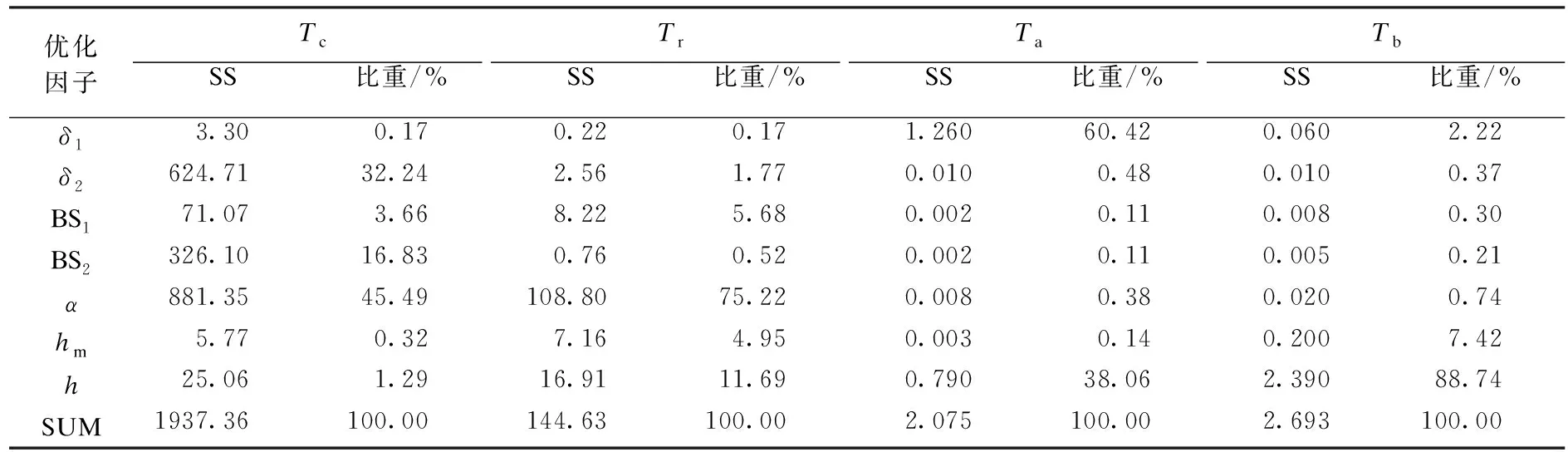
表7 各优化因子对优化目标影响比重Table 7 The proportion of the influence of each optimization factor on the optimization goal

1.3 最优参数组合与结果对比

根据图2与表7分析可得：

(1) 定子轭部厚度h使得内外转子的转矩变小，其原因可能是内、外电机磁场在定子中的耦合加剧，可以考虑在定子轭部设置适当厚度的隔磁环.

(2) 通过优化δ1可以增大磁阻转子的转矩.BS1对4个优化目标的影响程度都较小，BS2虽然对齿槽转矩有较大影响，但不是主要影响因素.

(3) 内电机参数对外电机难以产生较大影响，外电机参数也难以对内电机产生大的影响，定子轭部厚度可同时影响两者的转矩.

(4) 对于内转子转矩而言，内气隙长度和定子轭部厚度对其影响最大.当Ta达到最优值时，h的取值恰好也是转矩脉动的最优值，δ1却不是转矩脉动的最优值，但δ1对转矩脉动的影响很小，所以此时h和δ1的取值同时满足了转矩和转矩脉动的要求.

(5) 改变α的值可以大幅降低转矩脉动，α的取值对Ta的影响却很小.类似的分析同样存在于Tb和转矩脉动之间，同时在选取优化参数时，当转矩和转矩脉动无法同时达到最优值时，优先选择能够使转矩脉动达到最优值的参数组合.

综合考虑上述因素，优化因子取值如表8所示.

表8 各优化因子取值Table 8 Values of optimization factors

利用表8数据在Ansys Maxwell中建立电机模型，进行转矩特性的仿真，得到优化前后的各优化目标的数据对比，如表9所示.

表9 优化目标优化前后数据对比Table 9 Comparison of optimization objectives before and after optimization

由表9可知：内、外转子转矩较优化前均得到了提高；转矩脉动降低了56.10%，提高了电机的输出转矩的平稳性；齿槽转矩却比之前略高，但不超过内转子和外转子转矩和的5%，齿槽转矩较小.实际上，像这样的多目标优化中所取的因子越多，这种矛盾出现的可能性也会越大，这个时候必须做出取舍.本实验倾向了优化的主要目标转矩脉动，而这也是多目标优化不同于单目标优化的地方.优化后的电机参数发生这样的变化：内定子槽宽增加了0.1 mm；极弧系数由0.7变为了0.8；定子轭部厚度增加.优化后的内转子依旧能够平稳运行，外转子的转矩脉动显著降低，电机的稳定性获得提高.极弧系数的改变大大改善了外转子的转矩脉动，气隙径向磁密波形呈平顶波，对径向磁密进行傅里叶分解，谐波保持在很低的范围内.

2 结 论

本文应用田口法对永磁磁阻双转子混合电机这种新型的双转子电机进行转矩性能优化.在对永磁磁阻双转子混合电机较多的可优化参数进行分析后，权衡取舍选取了7个参数作为优化因子.通过正交实验和数据分析，最终得出一组最优的参数组合并进行仿真，实现了对目标的有效优化：在增大内、外转子转矩的同时，大幅度降低了电机的转矩脉动；齿槽转矩虽有增加，但其值小于电机的总转矩的5%；永磁磁阻双转子混合电机的输出转矩性能大大提高.本研究验证了田口法在新型永磁磁阻双转子混合电机这种复杂电机中的多目标优化的有效性，也为双转子电机的优化设计提供了参考.