考虑剪力滞效应及剪切变形的蝶形腹板箱梁挠度分析

2022-10-13张云飞陈建兵

苏州科技大学学报(工程技术版) 2022年3期

张云飞，陈建兵，周晨

（1.苏州科技大学土木工程学院，江苏苏州 215011；2.中交一公局第二工程有限公司，江苏苏州 215011）

蝶形腹板箱梁是一种全新的桥梁结构形式，与传统混凝土箱梁桥相比，其具有自重轻、养护费用低、施工周期短、造型优美等优势[1]。该结构主要特点在于腹板呈蝴蝶形，传力形式类似于“X”形双层沃伦桁架结构[2]，荷载作用下，分为主压应力区域和主拉应力区域。此外，在腹板材料的使用方面选用高强度钢纤维混凝土，其目的是防止腹板主拉应力区域产生裂缝，避免腹板失效。

世界上第一座蝶形腹板箱梁桥——田久保川桥由日本于2013年建成，如图1所示。国外学者对该结构进行了一系列研究，Akio Kasuga对蝶形腹板箱梁结构进行了风洞试验，以研究其抗风性能，研究表明蝶形腹板的开孔结构提高了箱梁整体结构在扭转振动和垂荡振动下的气流稳定性[3]；Yuki Kaminaga以芥川大桥为研究对象介绍了蝶形腹板混凝土箱梁结构的施工方式、腹板构造及传力方式，并通过有限元模型验证了腹板的传力方式类似于双层沃伦桁架结构[4]。蝶形腹板在传力形式上虽然新颖，但在国内尚未有相关实桥，对其力学性能方面的研究也较少。为研究蝶形腹板箱梁的力学性能，焦广如等[5]通过制作蝶形腹板箱梁的试验模型，对模型三分点位置进行了双点对称加载，试验结果表明：在竖向荷载作用下，蝶形腹板接缝位置存在较大剪切变形，但箱梁整体仍具有良好的抗弯性能；朱子昊等[6]推导了蝶形腹板剪切变形计算公式，通过有限元验证了理论公式的准确性，并在有限元模型的基础上改变腹板厚度和主拉应力方向上张拉应力的大小，研究两者与腹板剪切变形的关系，研究表明增大腹板厚度及施加预应力可有效提高腹板承载力。

图1 田久保川桥形状图[1]

目前，在蝶形腹板箱梁的力学性能研究方面，关于结构变形的研究还不够全面，剪力滞效应对蝶形腹板箱梁变形的影响尚不明确。此外，蝶形腹板箱梁作为一种空腹式薄壁型箱梁结构，在受力过程中腹板将承受剪力作用，但腹板抗剪刚度较低，会导致腹板产生较大的剪切变形。因此，本文基于Timoshenko梁理论以及能量变分法原理，从剪力滞效应及腹板剪切变形两个角度考虑结构挠度变形，并提出相关公式，结合试验及有限元对理论结果加以验证，为该类桥梁的设计提供参考和理论依据。

1 基本方程的建立

1.1 控制微分方程的建立

为建立蝶形腹板箱梁剪力滞效应的控制微分方程，需做出如下假定[7]：

（1）蝶形腹板箱梁在竖向荷载作用下，结构横截面沿梁高度方向应变满足平截面假定；

（2）箱梁顶底板与蝶形腹板之间协同工作，性能良好；

（3）忽略蝶形腹板与混凝土顶底板之间的相对滑移。

1.2 基本原理

蝶形腹板混凝土箱梁外力荷载及横断面图如图2所示，在外力荷载q（z）的作用下，截面发生较大挠曲变形，为更好的描述箱梁截面任意一点的纵向位移，并考虑腹板剪切变形的影响，选取最大剪切转角位移差作为剪力滞广义位移[7]，则箱梁截面任意一点处的纵向位移u（x,y）、竖向位移ω可表示为

图2 外力荷载及蝶形腹板箱梁横截面示意简图

其中，φ（x）=ω'（x）-γ（x），ω（x）为组合梁竖向挠度；γ（x）为组合梁剪切变形值，γ（x）=αQ（x）/（GA），α=A/Aw，A为箱梁截面面积，Aw为箱梁截面腹板面积，G为剪切模量；ωζ（y）为剪力滞纵向翘曲位移差函数；U（x）为剪力滞广义位移函数。

蝶形腹板组合箱梁的剪力滞翘曲位移函数ωζ（y）选取三次抛物线型[8]，可以表示为

式中，D为使箱梁横截面满足轴向剪力滞翘曲应力平衡条件而考虑的常数位移值。根据箱梁截面轴力为零的平衡条件可知

箱梁截面分别由顶板、底板、翼缘板及腹板四部分组成，将各截面的剪力滞翘曲位移函数定义为ωζi（y）（i=1，2，3，4），式（4）可表示为

将式（3）代入式（5）可得

式中，A为箱梁横截面面积；At为顶板截面积，At=b1ts；Ac为翼板截面积，Ac=b2ts；Ab为底板截面积，Ab=b3tx；Aw为腹板截面积，Aw=（hs+hx-ts-tx）×2tw；A=At+Ac+Ab+Aw。

1.3 剪力滞控制微分方程

根据最小势能原理可知，处于平衡状态的结构体系总势能的一阶变分为零，即

式中，Vs为翼板的应变能；Vw为腹板应变能；W为外力势能。写出蝶形腹板箱梁总势能表达式为

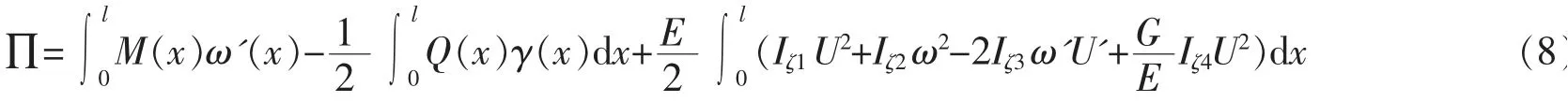
式中，Iζi（i=1,2,3,4）分别为蝶形腹板箱梁截面的几何特性值，具体表达式如下：

得到微分方程和边界条件为

整理可得

式中，n=Iζ2Iζ3/（Iζ1Iζ2-Iζ3）；k2=GIζ2Iζ4/[E（Iζ1Iζ2-I2ζ3）]

1.4 等效截面

蝶形腹板箱梁为空腹式结构，截面刚度沿梁长方向并非连续分布，因此需对空腹处截面进行等效处理。基于截面等效前后面积与惯性矩相等原则，将蝶形腹板的空腹部分等效成矩形，如图3所示。腹板高度为hw,腹板厚度为tw，开孔高度为d，开孔间距为d1,空腹部分面积为A1，惯性矩为I1面积等效后的空腹处矩形高度为hk，宽度为bk。按等效前后面积与惯性矩相等的原则[9]，即则有等效后空腹处截面如图4所示。将hk、bk代入箱梁横截面空腹处进行计算可得蝶形腹板箱梁截面空腹处惯性矩Ik为

图3 蝶形腹板箱梁等效尺寸

图4 空腹处等效截面

式中，y为各截面到形心距离；s为肋处矩形面积，I0为惯性矩为。

2 挠度方程的建立

蝶形腹板箱梁在剪力滞效应以及剪切变形下的挠度变形分为三部分，分别为初等梁理论下的挠度变形ω1，剪切变形引起的挠度变形ω2，以及剪力滞效应引起的附加挠度ω3。因此，剪力滞效应及剪切变形下蝶形腹板箱梁的挠度变形表达式为

测量不确定度是测量结果的科学表达，也是测量结果可靠性、可比性和可接受性的基础［1］。目前，中国各行业实验室为实现与国际接轨，开始进行国家实验室认可评审，目的是评价测定结果的准确性，需对检测过程进行不确定度评定。根据实验室认可准则要求，在分析检测过程中，需要建立并应用评定结果的不确定度程序［2］。目前国内外文献报道关于分析方法测量不确定度的评定多见于食品分析［3，4］、环境分析［5，6］等领域，且在药物分析领域也得到了一定的应用［7，8］，并将得到越来越多分析工作者的重视。测量不确定度是对测量结果的定量表征，不确定度越小，测量结果越准，使用价值越大［2］。

2.1 蝶形腹板箱梁弯曲

为分析初等梁理论下，蝶形腹板箱梁的弯曲变形，提出如下假定[10]：

（1）忽略蝶形腹板对抗弯承载力的贡献；

（2）忽略混凝土顶底板的剪切变形；

（3）蝶形腹板与混凝土顶底板均为理想的弹性材料；顶底板与腹板之间协同受力，工作良好。

当简支梁受竖向荷载作用，其加载示意图如图5所示。

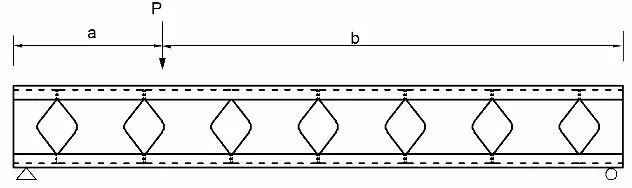
图5 集中荷载下简支梁加载图

当0≤x≤a时，简支梁内力和挠度表达式

当a≤x≤l时，简支梁内力和挠度表达式

式中，E为混凝土的弹性模量。

2.2 蝶形腹板箱梁的剪切变形

蝶形腹板箱梁结构是一种弱腹式薄壁结构。荷载作用时，其剪力大部分由蝶形腹板承担，并且由于腹板沿梁长方向不连续的原因，在蝶形腹板接缝处易产生较大的剪切变形。因此在计算剪力滞下结构的挠度变形时，剪切变形是一项不可忽略的因素。

在计算蝶形腹板的剪切变形之前，先引入如下假定[11]：

（1）忽略蝶形腹板的纵向抗弯刚度；

（2）忽略混凝土顶、底板的剪切变形，仅考虑腹板的剪切变形；

（3）蝶形腹板与混凝土板均为理想的弹性体，混凝土顶、底板的挠曲变形一致。

剪力单独作用时，组合梁挠度曲线上任意点的斜率等于该处截面的剪应变，则

式中，k0为剪力不均匀系数，与截面形状有关，本文取1。Gw为蝶形腹板的剪切模量，Aw为蝶形腹板等效后的横截面面积。

将以上几式代入式（17）可得

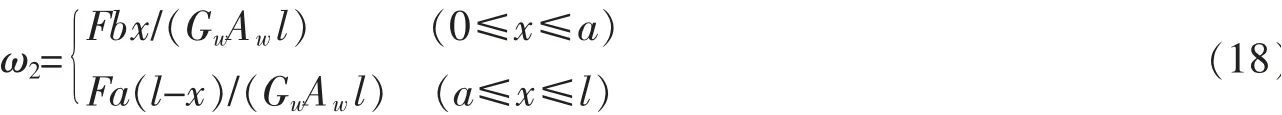
2.3 剪力滞效应引起的附加挠度

蝶形腹板箱梁的变形分为弯曲作用下的挠度变形，以及剪力滞效应下的附加挠度两部分。由前文U(x)的微分方程，并考虑U（x）的连续条件及边界条件如下[12]：

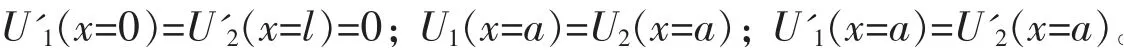
解得剪力滞效应引起的挠度方程为

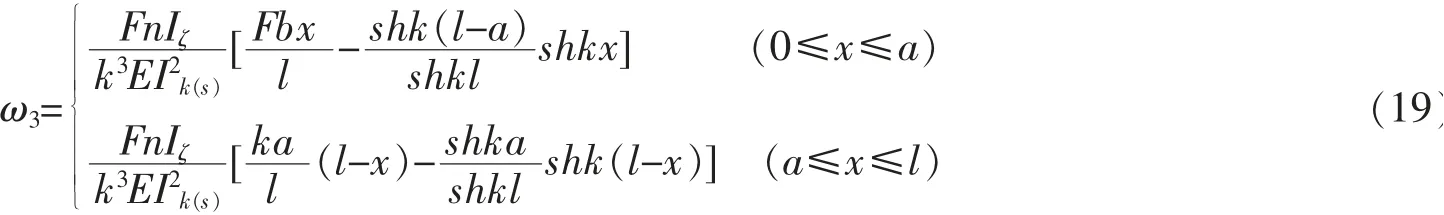
因此，考虑剪切变形与剪力滞效应引起的挠度方程可表达为

当蝶形腹板箱梁受均布荷载作用时，其加载示意图如图6所示。

图6 均布荷载下简支梁加载图

其弯矩和剪力表达式为

同理，可得挠曲线方程为

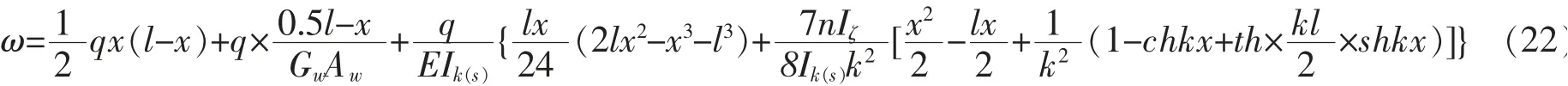
3 有限元模型的建立

3.1 有限元模型建立

运用Abaqus有限元软件建立蝶形腹板箱梁有限元模型，模型采用两种不同类型单元进行模拟，其中混凝土顶底板、腹板均采用实体单元（C3D4R），钢筋骨架采用线单元（T3D2）。钢筋网使用内置（Embedded region）约束,腹板与顶底板的连接采用绑定（Tie）约束，加载垫块和支座采用绑定约束，边界条件为简支，有限元模型如图7所示。

图7 蝶形腹板箱梁有限元模型

3.2 有限元模型的试验验证

为验证公式的正确性，制作了蝶形腹板箱梁试验梁模型。该梁结构形式为简支梁，梁全长3 570 mm，计算跨径为3 400 mm，箱梁横截面具体参数如图8所示。箱梁顶底板采用C30普通混凝土，蝶形腹板为C60钢纤维混凝土，具体尺寸如图9所示。蝶形腹板与顶底板之间由销钉和顶底板中的箍筋相连，起到剪力连接件的作用，能够有效地传递竖向剪力。为方便箱梁变形计算，在箱梁底部布置了7个位移计，测量其挠度，如图10所示；试验梁加载模型如图11所示。

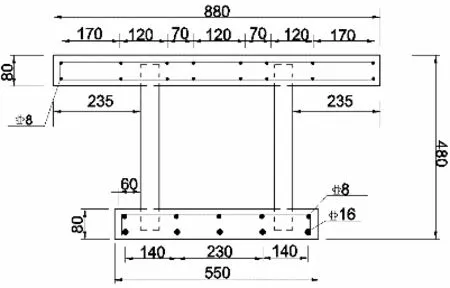
图8 截面基本尺寸

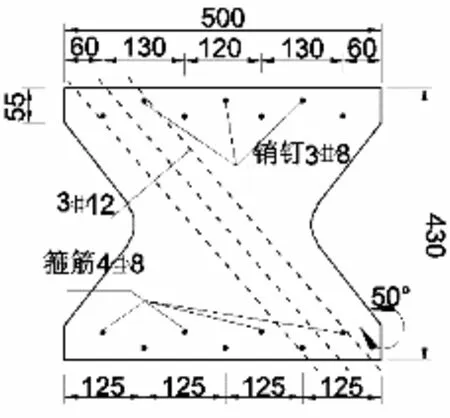
图9 蝶形腹板构造图

图10 位移计布置图

图11 蝶形腹板箱梁加载图

3.3 对比分析

蝶形腹板箱梁是一种弱腹式箱梁结构。在竖向荷载作用下，引起结构发生弯曲变形的因素有很多，其中剪切变形与剪力滞效应是引发挠度变形的两个重要因素，根据试验梁模型的相关参数，代入前文公式得到理论值，与文献[5]中不考虑剪切变形及剪力滞效应下的结构挠度变形进行对比，并结合试验值与有限元值分析，验证文中理论公式的准确性。

取P=85 kN下的试验值、有限元值、文献值及本文值进行分析，整理结果如图12所示，以及表1所列。

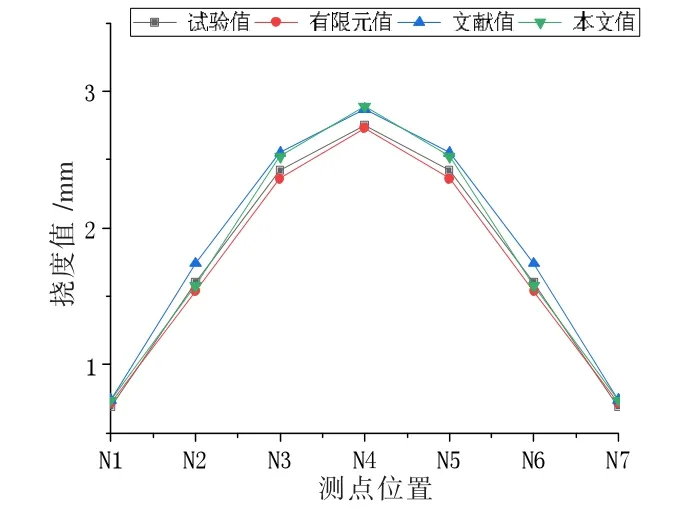
图12 集中荷载下蝶形腹板箱梁挠度变形对比图

表1 集中荷载下蝶形腹板箱梁挠度对比

由图12和表1可知，考虑剪力滞效应及剪切变形下的挠度值与文献值相比更加接近试验值，其中弯剪段的挠度值较文献值相比精度更高，跨中及支座位置的挠度值差距较小，说明集中荷载作用下剪力滞效应及剪切变形对蝶形腹板箱梁的挠度变形影响主要集中在弯剪段。在测点位置N2处，本文方法与文献方法所计算的误差较大，这是由于箱梁弯剪段受到剪力滞效应与剪切变形引起的挠度变形较大，并且空腹处截面进行截面等效时会产生一定的误差。

为研究均布荷载作用下，蝶形腹板箱梁挠度变形情况，取均布荷载q=10 kN/m，将截面特征值、荷载及相关截面参数代入式（22）中将理论值与有限元值以及文献值相比较得出结果如表2及图13所示。

由表2及图13可知，考虑剪力滞效应及剪切变形下的挠度值与文献值相比更加接近有限元值，全梁段精度与文献值相比均有提高。因此在均布荷载作用下，考虑剪力滞效应及剪切变形下的挠度计算更为精确。此外，在均布荷载作用下，剪力滞效应及剪切变形对蝶形腹板箱梁挠度的影响主要集中在箱梁的弯剪段。在测点N1、N2处的本文值与有限元值误差较大，这是由于有限元的数值计算无法精确模拟出试验梁的真实挠度情况，并且N2处于弯剪段受到剪力滞与剪切变形影响的因素较多，因此计算结果存在一定的误差。