板件屈服耗能支撑恢复力模型研究
2022-10-13张鹏杰赵宝成
张鹏杰,赵宝成
(苏州科技大学 江苏省结构工程重点实验室,江苏 苏州 215011)
支撑斜杆在地震作用下容易发生受压失稳,在失稳后,支撑的承载力会明显下降。国内外学者提出了各种耗能支撑形式,比如防屈曲支撑[1]、在结构上安装阻尼器[2]、设置耗能连梁[3]等方式。文献[4]采用在传统支撑的基础上加入金属阻尼器的设计思路,提出了一种新型腹板开孔屈服耗能支撑,构造如图1所示,开孔腹板为薄弱部位,在水平荷载作用下,开孔腹板首先进入塑性变形耗能,整个开孔腹板发生剪切破坏时,腹板开孔耗能支撑的承载力低于支撑的屈曲荷载,有效避免了支撑发生整体失稳破坏。在此基础上,发展了一系列不同形式的板件屈服耗能支撑[5-7]。然而现有的研究成果中,主要对板件屈服耗能支撑的滞回性能研究较多,对恢复力模型的研究较少。
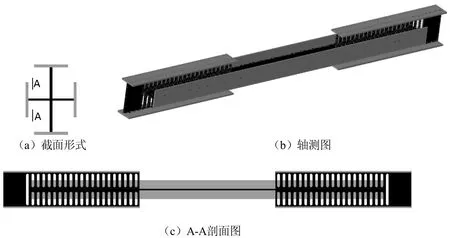
图1 腹板开孔耗能支撑
恢复力模型是根据大量从试验中获得的恢复力与变形的关系曲线经适当抽象和简化而得到的实用数学模型,是结构试件的抗震性能在结构弹塑性地震反应分析中的具体体现,恢复力模型的确定是结构进行弹塑性分析中最基础的一环[8-10]。根据模型曲线形状,恢复力模型分为折线形恢复力模型和曲线型恢复力模型两—————————大类,折线形恢复力模型物理意义清晰,使用方便,但在屈服点前后的滞回曲线存在刚度不连续点,导致结构非弹性地震动力反应分析过程不易收敛且存在误差累计的情况,使得分析结果与实际情况不符。曲线型恢复力模型对各种滞回曲线都能较好的近似描述,且刚度变化连续,模拟精度较高,与工程实际比较符合。Bouc-Wen模型具有曲线光滑、易于计算收敛、曲线具有极强的适应性,仅用一个微分方程就可以表现出复杂曲线的滞回特性的优势。综合上述原因,本文将采用Bouc-Wen模型,对新型耗能支撑基于Bouc-Wen模型的参数进行识别,得到该新型耗能支撑的参数取值。
1 Bouc-Wen模型
经Bouc和Wen的研究[11-12],提出了光滑的恢复力曲线的微分形式

式中:R为支撑的轴向恢复力,u为结构相对位移;k为支撑的轴向弹性刚度,α为屈服后刚度与弹性刚度的比值,z为结构滞回位移,A、β、γ为控制滞回环形状的参数;n为屈服的尖锐程度参数。
Baber和Wen引入强度和刚度退化特征改进Bouc-Wen模型[13],Baber和Noori考虑了捏缩滑移效应进一步改进Bouc-Wen模型[14],经过多位学者对Bouc-Wen模型的不断改进,Bouc-Wen模型由最初的5个参数发展到13个参数,改进型Bouc-Wen模型的恢复力曲线微分关系式

其中,式(4)与滞回环所消耗的总能量呈线性关系,用于衡量刚度和强度退化的参数。其中k、α、z、A,n,β,γ与Bouc-Wen模型参数含义相同,δν为强度退化因子,δη为刚度退化因子,ζ为总滑移的尺寸,q为缩聚初始量,p为缩聚的量级,ψ为缩聚的量级,δψ为缩聚率,λ为缩聚的严重程度与相互作用的比率。
图2和图3对比发现相关参数的引用使改进型Bouc-Wen模型在反复荷载作用下能够很好地模拟试件所具有的捏拢效应等一系列曲线特性,同时增加了参数拟合的难度。为了更好的对比两种模型的区别,本文对两种模型均给出试件BDW-1的拟合对比情况,具体对比见下文。
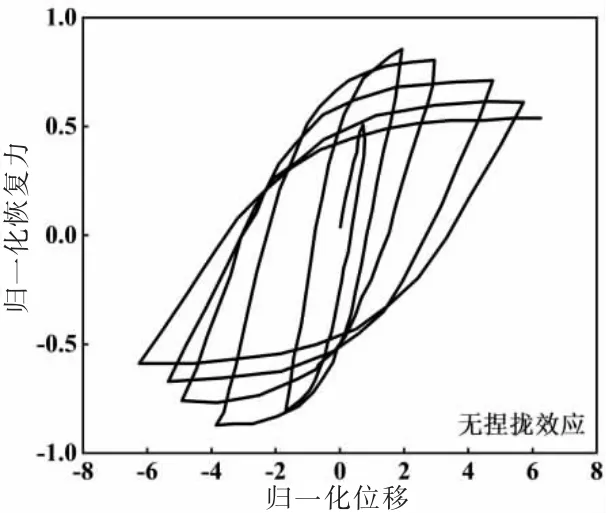
图2 Bouc-Wen模型对应曲线

图3 改进型Bouc-Wen模型对应曲线
2 板件屈服耗能支撑试验简介
本文采用文献[5]、文献[6]、文献[7]的耗能支撑试件进行分析。其中文献[5]的试件为腹板开孔耗能支撑,耗能支撑采用交叉双工字钢十字形截面,两端与框架连接的工字钢,腹板开长圆孔,通过腹板开槽与中间工字钢拼接,在荷载作用下,通过开孔腹板的孔间板件剪切屈服耗散能量。试件BDW-1在端部设置一层开孔腹板,如图4(a)所示。试件BDW-2在端部对称设置两层开孔腹板,试件BDW-3在端部设置三层开孔腹板。
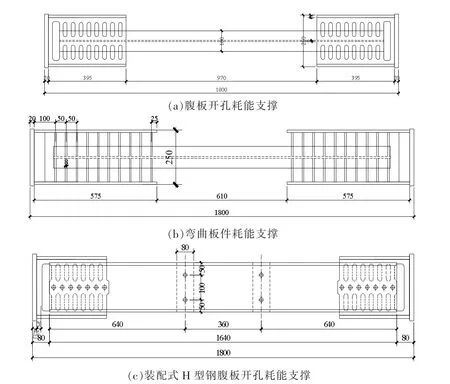
图4 耗能支撑试件[5]
在文献[5]设计思路的基础上,文献[6]的构件将耗能部件改为连接板,通过平行设置的连接板将中间工字钢和翼缘连接,在荷载作用下通过连接板弯曲耗能可极大地提高试件的变形能力。试件BDP-1与BDP-2在构造上一致,如图4(b)所示,具体差距体现在连接板的尺寸区别。文献[7]的试件为装配式H型钢腹板开孔耗能支撑,H型钢与槽钢采用螺栓连接,在荷载作用下,试件通过H型钢开孔腹板的孔间短柱剪切屈服耗能。试件在构造上一致,如图4(c)所示,差异在开孔形式上,试件BDC-1开长圆孔,试件BDC-2开椭圆孔,试件BDC-3开菱形孔。加载的试验装置及加载制度均参考文献[7],具体构件的各项参数见表1。
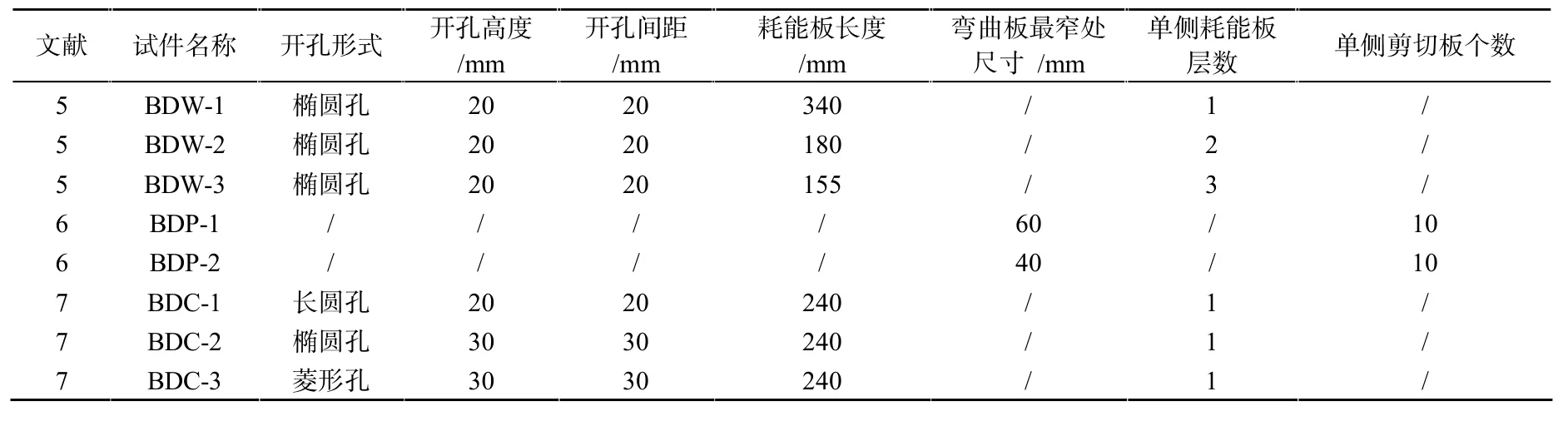
表1 各试件参数
3 参数拟合方法
本文采用Excel的规划求解工具进行复杂非线性方程的最优拟合,对Bouc-Wen模型中的参数进行识别[15],该方法原理简单易操作,避免复杂的编程,且拟合效果较好。
3.1 拟合参数准备工作
3.1.1 弹性刚度k
在对Bouc-Wen模型中的参数进行识别之前,可先由试件中所含的各连接段的长度和面积计算试件的初始刚度,根据试件截面形式的不同给出各试件的拟合公式。
BDW(BDC)系列初始刚度Kz拟合公式
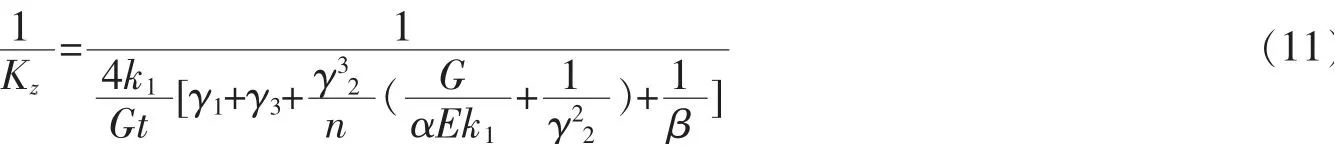
其中,G为剪切模量;k1为截面剪切不均匀系数(矩形截面为1.2);截面影响系数γ1=l1/L、γ2=l2/Hc、γ3=l1/L0,具体尺寸参数见图5;n为孔间短柱个数,α是考虑了边界条件以及开孔对弯曲刚度的影响系数,α=l2h0/(30hc);E为弹性模量。β取值为400时得到BDW系列初始刚度拟合公式的局部最优解,β取值为485时得到BDC系列初始刚度拟合公式的局部最优解。BDP系列初始刚度(Kz)拟合公式为
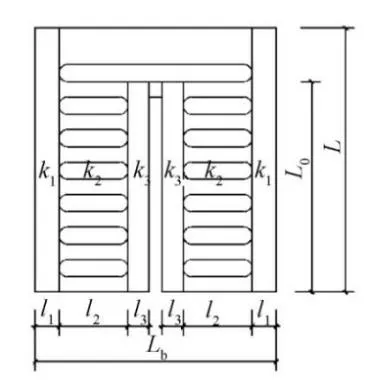
图5 开口腹板刚度划分
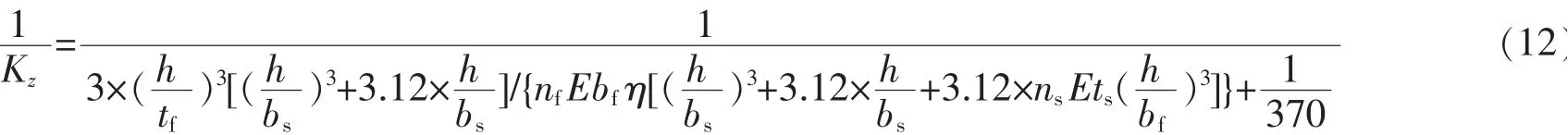
其中,具体尺寸参数见图6,nf为弯曲板个数,ns为剪切板个数,t=ts=tf为弯曲板的厚度,E为弹性模量。η与ζ关系式为
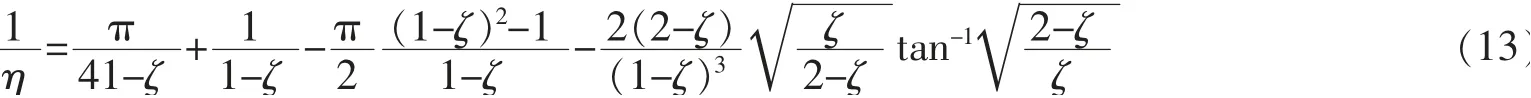
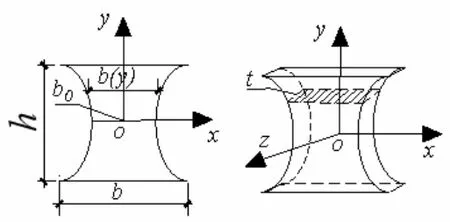
图6 弯曲板示意图
还可由试验数据中未进入塑性阶段的平直段进行线性拟合,拟合所得到的斜率即为初始刚度。由于钢材的弹性模量离散型较小,两种方法所得的结果误差很小,所以本文采用拟合试验数据的斜率得到初始刚度,结果见表2。

表2 弹性刚度及α的数值
3.1.2 屈服后刚度
α为屈服后刚度与弹性刚度的比值,屈服后刚度的确定方法有3种:(1)根据试验所得数据,在塑性变形后期,支撑屈服后的平直段比较明显,可以对平直段的数据进行线性拟合,所得斜率即为屈服后刚度。由式(1)反算出内变量z,当z保持最大值不变时即为平直段。(2)当加载位移等于5倍的屈服位移时,内部滞后变量微小,即此时恢复力与加载位移成线性关系。(3)通过加载位移相差一定值的两个滞回环识别屈服后强度,一般试验中的位移加载制度不符合该条件。
根据本文的参数敏感度分析可知,屈服后刚度α对Bouc-Wen模型的影响较小,根据现有试验数据对屈服后刚度α进行了直线拟合,可供参考,直线拟合结果为

式中Dy为屈服位移。
3.1.3 屈服位移Dy
在往返加载的曲线中,屈服平台不明显无法直接从曲线上判断屈服位移。屈服位移的识别方法采用对弹性阶段的数据以及非弹性阶段的数据进行直线方程拟合,两条直线的交点近似认为是屈服位移。
根据上述方法使用Origin软件对试件所得试验数据进行处理,处理结果见表2。
3.2 拟合模型参数
给定u=0、内变量z=0以及剩余未知参数一个初始值,通过公式(2)计算出所有的内变量z,根据公式(1)和未知参数的初值得到拟合后的恢复力Fmi。参数拟合方法是构造以试验所得的恢复力与拟合恢复力的均方根误差作为目标函数

式中,Fti为试验得到的恢复力数据点Fmi为拟合得到的恢复力数据点,m为试验所采集的数据点数。
通过Excel中的规划求解工具不断迭代求解目标函数的最小值,以连续5次迭代目标函数均不发生较大的数值变化为终止条件,从而确定Bouc-Wen模型中的未知参数的一组拟合值。通过上述方法拟合各试件的未知参数,以迭代结束为最终结果。其最终参数取值见表3,由于屈服位移离散性较小,可将所得未知参数的取值(y)与屈服位移(x)进行函数拟合,为实际工程使用提供参考,具体拟合函数见表4。
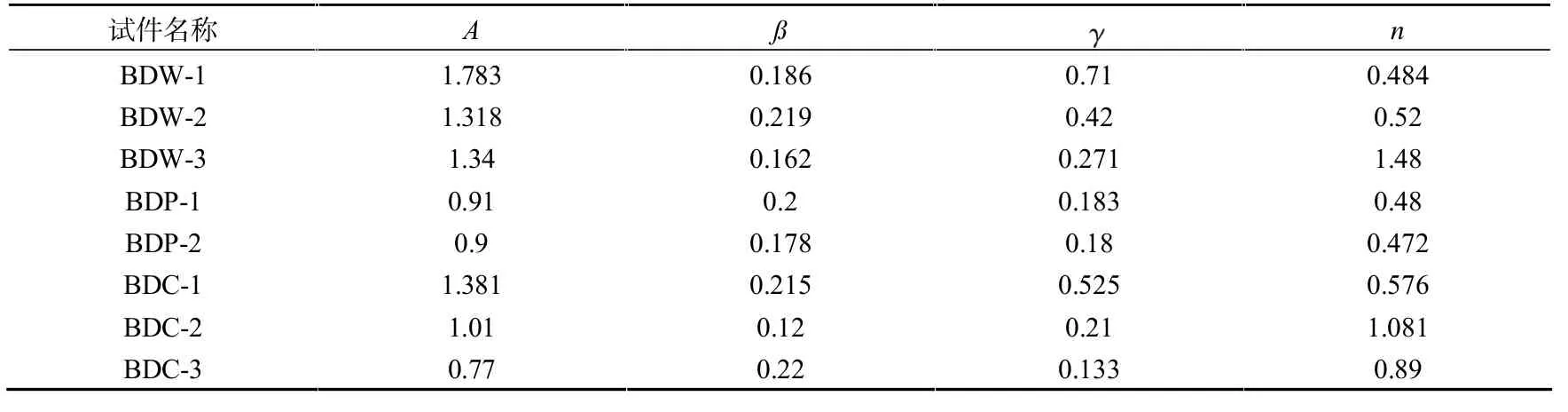
表3 拟合Bouc-Wen模型中的未知参数

表4 拟合未知参数函数关系及建议取值范围
图7~图14为试件采用Bouc-Wen模型拟合的滞回曲线和试验滞回曲线的对比,根据对比可知,前期拟合程度较高,其基本走势和特征点均匹配较好,为了更好的对比拟合的程度,分别从滞回曲线、骨架曲线、刚度退化、耗能能力角度分析拟合程度,具体对比情况见图7~图14。
通过图7~图14及表5可知,各试件的试验与拟合曲线吻合程度较高,各特征点吻合程度高,体现在拟合的骨架曲线以及刚度退化曲线与基本试验曲线吻合程度。针对BDW-2试件在后期试验与拟合曲线尖锐度不同、BDC-2试件在试验曲线波折处与拟合曲线吻合程度不高的等滞回曲线局部不吻合的问题,原因是对于为“目标函数求最小值法”,是通过不断改变未知参数的取值使公式中所求的拟合恢复力与真实恢复力无限接近,从而确定最优参数取值,所得到的参数值是整体曲线的最优解,无法通过调整参数取值达到服务于局部的效果,所以该法所得的参数取值下,试验滞回曲线与拟合滞回曲线无法完全重合,极值处的尖锐度以及前期后期的拟合精度误差都是在符合整体取值前提下的最优情况。由于试验滞回曲线与拟合滞回曲线不能完全重合,而累计滞回耗能是根据滞回曲线的数据计算所得,所以累计滞回耗能也是存在一定的误差。对于各试件拟合过程中存在的误差,表5给出精准的拟合误差,其中骨架曲线以正负向极值点处对应值做为误差分析点,刚度退化曲线以初始刚度作为误差分析点,耗能能力以累计耗能最大值作为误差分析点。

表5 Bouc-Wen模型的拟合误差

图7 BDW-1试件拟合和试验特征曲线的对比
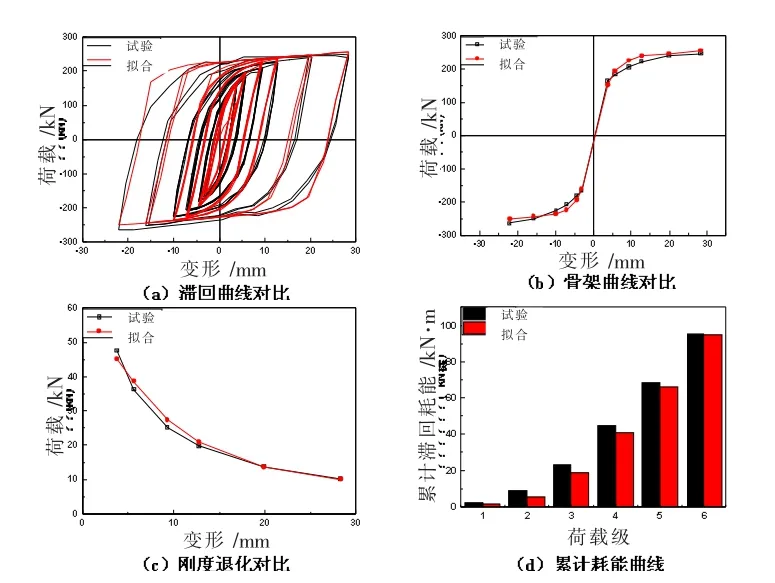
图8 BDW-2试件拟合和试验特征曲线的对比

图9 BDW-3试件拟合和试验特征曲线的对比
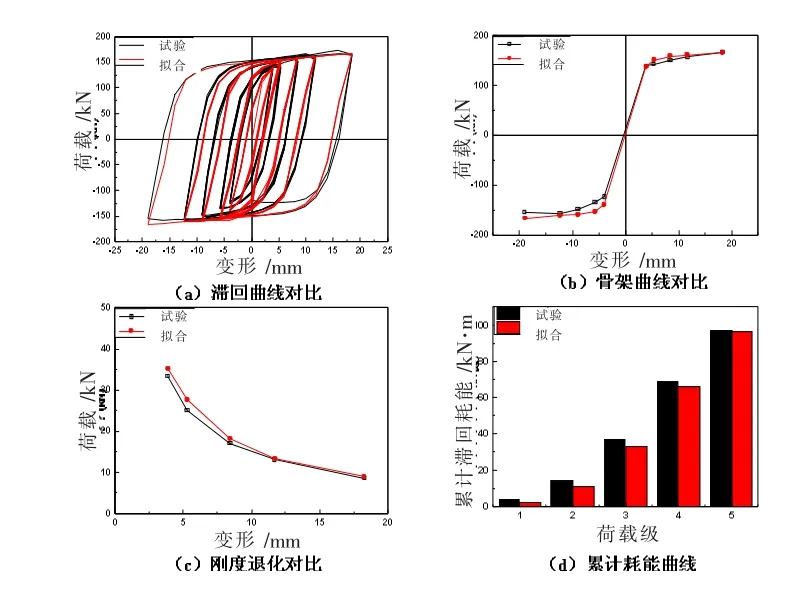
图10 BDC-1试件拟合和试验特征曲线的对比
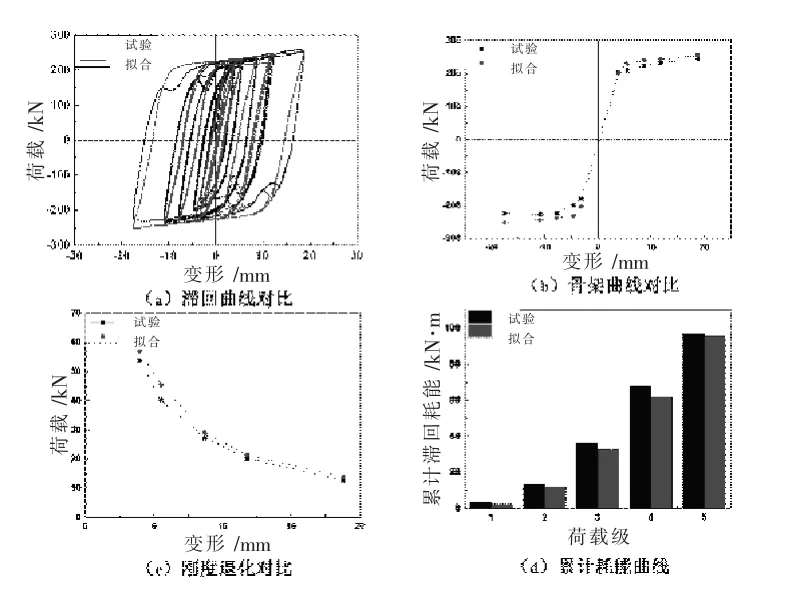
图11 BDC-2试件拟合和试验特征曲线的对比

图12 BDC-3试件拟合和试验特征曲线的对比

图13 BDP-1试件拟合和试验特征曲线的对比
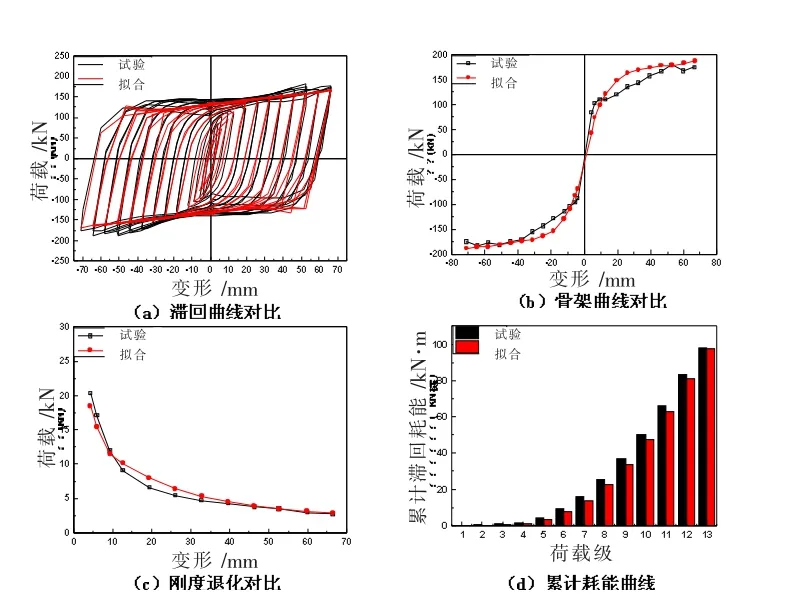
图14 BDP-2试件拟合和试验特征曲线的对比
采用上述方法拟合改进型Bouc-Wen模型的参数,当采用A=353.8,α=0.033 7,β=0.024,γ=0.003 25,n=0.62,δy=5.712,δn=0.0037,ζs=0.99,q=0,p=0.418,ψ=96.878,δψ=0,λ=1.5的参考取值时,可得到一组符合目标函数最小值时的参数取值。下图为BDW-1试件采用改进型Bouc-Wen模型拟合和试验滞回曲线的对比,改进后的Bouc-Wen模型很好地拟合了滞回曲线的拉压不对称以及曲线存在小程度的捏缩,在骨架曲线与刚度退化曲线方面存在一定的误差,但从累计滞回耗能角度,拟合曲线与试验曲线基本保持一致,具体对比情况见图15。
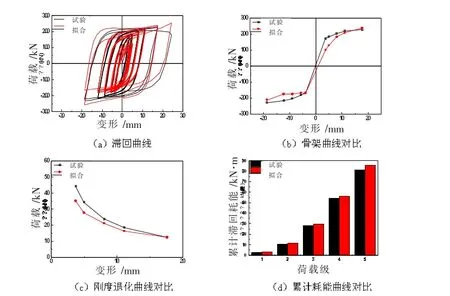
图15 BDW-1试件拟合和试验特征曲线的对比
通过图16拟合BDW-1试件的试验与拟合结果对比图可知,采用本文的拟合方法,无论是Bouc-Wen模型还是改进型Bouc-Wen模型的拟合结果均存在部分误差,无法达到与试验曲线完全一致,但改进型Bouc-Wen模型在转折点区域与试验曲线走势相同,而Bouc-Wen模型在转折点处较为尖锐。由于Bouc-Wen模型相较于改进型Bouc-Wen模型的参数较少,较为基础,使用方便,且将改进型Bouc-Wen模型中相关参数设置为0,就是另一种形式的Bouc-Wen模型。所以本文仅针对Bouc-Wen模型做出参数灵敏度分析。

图16 BDW-1试件的拟合滞回曲线对比
3.3 参数灵敏度分析
在Bouc-Wen模型参数拟合方法上,常用的拟合方法有遗传算法、最小二乘法,两者是基于数值求解的拟合方法,取任意初值时难以保证全局收敛。而退火算法、粒子群算法是基于优化技术的拟合方法,识别效率较低,耗时较久[16]。由于Bouc-Wen模型中的参数较多,在计算中需要固定一些低灵敏度的参数来简化公式,且对于拟合结果受初值影响的拟合方法,可通过参考参数取值变化对滞回曲线的影响来调整参数初始值,同时为后面改进公式提供参考。本文将对BDW-1试件采用单参数变化法对各参数进行分析,即将分析参数变化为拟合参数的-50%、-25%、25%、50%,固定其他参数。通过对比滞回曲线的变化,得到单参数对滞回曲线形状的影响。
3.3.1 初始刚度k初始刚度k的数值调整对滞回曲线的影响,本质上是简单的放大了拟合后的恢复力。由于其他参数此时为定值,公式(2)里中间变量z的求解由多元非线性的数值求根变为一元非线性函数求解,此时在(1)里变量u、中间变量z及α均为定值,所以参数k的数值调整为原有恢复力倍数调整。由于初始刚度通常数值较大,所以初始刚度k的数值调整对滞回曲线的影响也较大,通过观察图17,发现随着初始刚度的增加,滞回环整体的走势及所包围的面积也明显增加,随之极限承载力也随之增加,初始刚度k的变化对整个滞回曲线的饱满程度有较大的影响。

图17 参数k的敏感度分析
3.3.2 刚度比α
参数α的数值调整对滞回曲线的影响与初始刚度k相同,由于初始刚度往往远大于屈服后刚度,所以参数α的数值的较小,因此参数α的数值调整对滞回曲线的影响较小。通过观察图18,发现随着刚度比的增加,滞回环的饱满程度变化较小,极限承载力也没有明显的变化,仅对整个滞回曲线的总体滞回刚度变化影响较大。
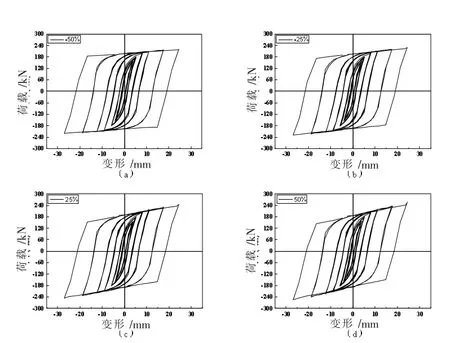
图18 参数α的敏感度分析
3.3.3 形状控制参数A
参数A的数值调整对滞回曲线的影响,本质上是一元非线性多项式函数求解的问题。根据公式(16)可知,当参数A的数值调整时,由于剩余参数均为定值,公式转化为中间就是变量z的求解问题,最终由变量z求解后通过公式(1)来影响滞回曲线。通过观察图19,发现随着形状控制参数A的增加,滞回环的形状由凌乱扁长状逐渐饱满,其所包围的面积也在增加。参数A的变化增强了滞回环的多样性及适用性,关于参数A的是否冗余还是需要具体分析。当参数A的数值在减少为原本的50%后,其拟合效果较差,形状控制参数A对滞回曲线的总体变化趋势影响较大。

图19 参数A的敏感度分析

3.3.4 形状控制参数β
参数β的数值调整对滞回曲线的影响与参数A本质是相同的,参数β的数值求解公式为(17)。
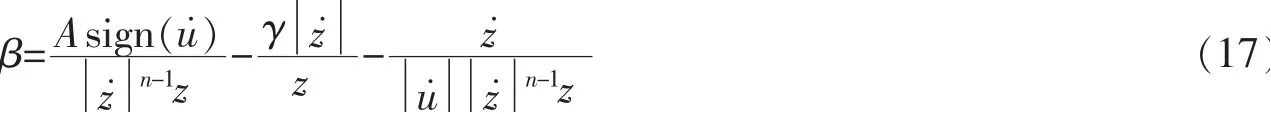
通过观察图20,发现随着形状控制参数β的增加,滞回环的形状由狭长逐渐饱满,但极限承载力呈逐渐降低的趋势,参数β的变化使得滞回环的形状变化较大,但形状控制参数β对整个滞回曲线的总体变化趋势影响较小。

图20 参数β的敏感度分析
3.3.5 形状控制参数γ
参数γ的数值调整对滞回曲线的影响与参数A本质是相同的,参数γ的数值求解公式为(18)。通过观察图21,发现随着形状控制参数γ的增加,滞回环的形状逐渐由饱满变得平缓,极限承载力也逐渐减小,且当参数γ在增加50%后,其拟合效果较差,形状控制参数γ对整个滞回曲线的饱满程度影响很大。
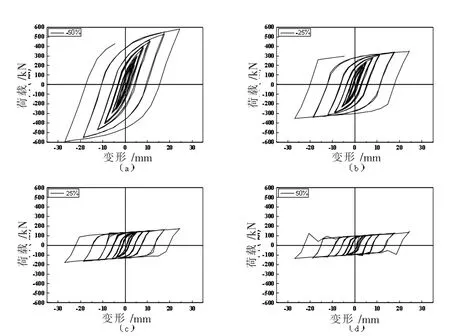
图21 参数γ的敏感度分析

3.3.6 形状控制参数n
参数n的数值调整对滞回曲线的影响,本质上是一元非线性对数函数求解的问题。参数n的数值求解公式为(19),参数n的调整转化为中间就是变量z的求解问题,最终由变量z影响滞回曲线的变化,因为公式(19)求解过程比较复杂,所以在拟合过程中需要慎重调节参数n的取值范围。通过观察图22,发现随着形状控制参数n的增加,滞回环的形状由尖锐的“S”形变得平缓,其对极限承载力的范围影响较大,同时参数n在增加为原本数值的50%后,其拟合效果存在多处不规则的变化,参数n对滞回环的整体走势及饱满程度影响很大。

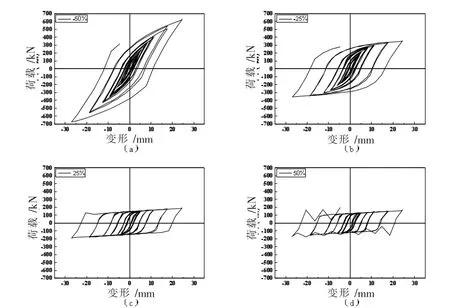
图22 参数n的敏感度分析
4 结论
本文对八根的试件采用试验与拟合结果对比的方法来确定该系列试件Bouc-Wen模型中的参数,对比滞回曲线、骨架曲线、累计耗能曲线显示该方法得到了较好的识别效果,并得到以下结论:
(1)对比发现两种模型各有优缺点,Bouc-Wen模型在骨架曲线和刚度退化曲线方面吻合度较高,改进型Bouc-Wen模型则在滞回曲线和累计耗能方面拟合较好。
(2)拟合参数β的取值较为稳定,可考虑取值在0.12至0.22之间,拟合参数α可考虑取值在0.01至0.03之间。对于Bouc-Wen模型拟合的参数数值,其中参数A、β、n与屈服位移之间均符合二次函数关系,参数β与参数γ之间呈一定的线性关系。
(3)当单参数的数值变化为-50%或50%时,滞回环在后期容易出现不规则波动,适当的调整初始参数的变化范围在-25%到25%之间,滞回曲线更容易呈饱满的形状。
(4)参数α幅值变化对滞回刚度影响较大,但相对其他参数幅值变化对滞回环的影响,参数α对滞回环的影响最小,而参数A、γ、n的变化对滞回环的形状影响最大,其余参数的变化对滞回环形状改变均有不同程度上的影响。
