基于iGMAS的北斗导航卫星原子钟性能评估

廉吉庆，张文玺，张金海，王世伟，陆 昉，翟 浩，崔敬忠，刘志栋

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

0 引言

近年来卫星导航技术发展迅速，多个国家或组织开展了全球卫星导航系统（Global Navigation Satellite System，GNSS）的建设。美国是最早建设卫星导航系统的国家，经过近半个世纪的发展，目前美国的全球定位系统（Global Positioning System，GPS）已进入GPS III阶段。2020年6月我国自主建设、独立运行的北斗三号卫星导航系统全面建设完成，并向全球提供导航定位授时服务。卫星导航系统是以时间测量为基础的系统，导航卫星通过测量卫星与接收机之间信号发送与接收的时间，解算位置信息，因此时间系统是卫星导航系统运行的基础。星载原子钟作为卫星导航系统上的时间基准，是导航卫星的关键核心部件。根据北斗卫星导航系统星座信息[1]，北斗二号卫星搭载了高精度铷原子钟，北斗三号搭载了性能更好的铷原子钟和氢原子钟，另外，北斗三号试验星还搭载了国产铯原子钟进行性能验证[2-3]。本文介绍了星载原子钟性能评估的主要参数，并利用全球连续监测评估系统（International GNSS Monitoring and Assessment System，iGMAS）提供的2019年12月到2021年2月期间钟差数据，分析和比较目前在轨应用的北斗二号卫星铷原子钟、北斗三号卫星铷原子钟和氢原子钟的各项性能，为原子钟研制人员提供参考数据。

1 星载原子钟的性能参数

评估星载原子钟性能的参数有三个，分别为频率准确度、频率稳定度和频率漂移率。

频率准确度表征原子钟输出信号频率与标称频率的吻合程度，是被测原子钟输出频率偏离标称频率的相对数值，由式（1）表示。从式中可以看出，频率准确度是有正负的。由于输出频率有短期的波动，实际频率准确度通常取采样时间1 h以上的数据计算平均值[4]。

频率漂移率表征原子钟输出频率随时间变化的程度，是衡量原子钟自主守时能力的重要参数，工程使用中通常以1天为单位对原子钟的频率漂移率进行测算，即天漂移。影响原子钟频率漂移的因素是多方面的，如控制电路元器件的老化、物理部分内部状态的稳定程度以及外部电磁和热环境的变化等。部分文献认为原子钟的频率变化是单调的，即频率漂移率的正负是不变的，但在实际应用中，原子钟的频率漂移可能呈现波动特性。基于频率准确度数据的漂移率D估计如式（2）所示[5]：

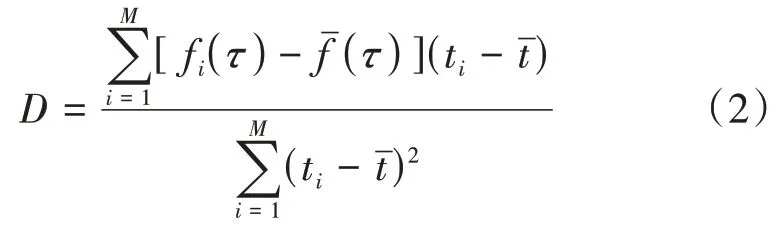
式中：fi(τ)为ti时刻原子钟的频率准确度，i=1，2，3…，M；M是取样时间为τ的总样本数；τ为取样时间；(τ)为频率准确度平均值

频率稳定度是衡量原子钟性能的另一个重要参数，它表示了一定时间内原子钟输出频率的平均波动或变化情况，通常用阿伦方差或哈达玛方差表示。阿伦方差反映了原子钟输出频率的全部变化情况，哈达玛方差采用3点采样计算，是针对频率漂移率较大的原子钟提出的方差分析方法[6]。铷原子钟通常采用哈达玛方差计算稳定度，以消除线性漂移的影响；氢原子钟和铯钟直接采用阿伦方差表示稳定度。阿伦方差和哈达玛方差可以用钟差或频差数据表示[5，7-8]，由于相位是频率的积分，因此两种表述本质上相同。以频差为输入的阿伦方差σ2y(τ)和哈达玛方差Hσ2y(τ)计算式分别如式（3）和式（4）所示：

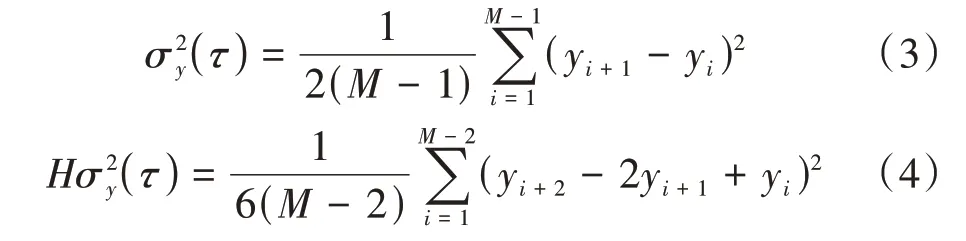
式中：yi是第i次取样时间τ内的平均频率准确度。

2 北斗导航卫星原子钟数据分析

2.1 数据来源与说明

iGMAS对用户提供8种产品，其中钟差数据反映了导航卫星在轨运行时间与地面标准时间的差值，可用于导航原子钟评估，包括最终钟差、快速钟差、超快速钟差和实时钟差四种类型，其中最终钟差精度最高。根据产品文件格式标准，iGMAS钟差产品的内容包括版本类型、文件类型、卫星标识符、卫星系统、参考钟数、钟差数据等，使用时主要关注的是钟差数据。钟差数据文件主要包含钟差数据类型、卫星PRN编号或接收机编号、历元时刻、数据个数及相应的数据，如表1所列。表中AS表示该行数据为卫星数据，最后两列数据分别为系统解算的原子钟在轨钟差数据和钟差标准差[9]。

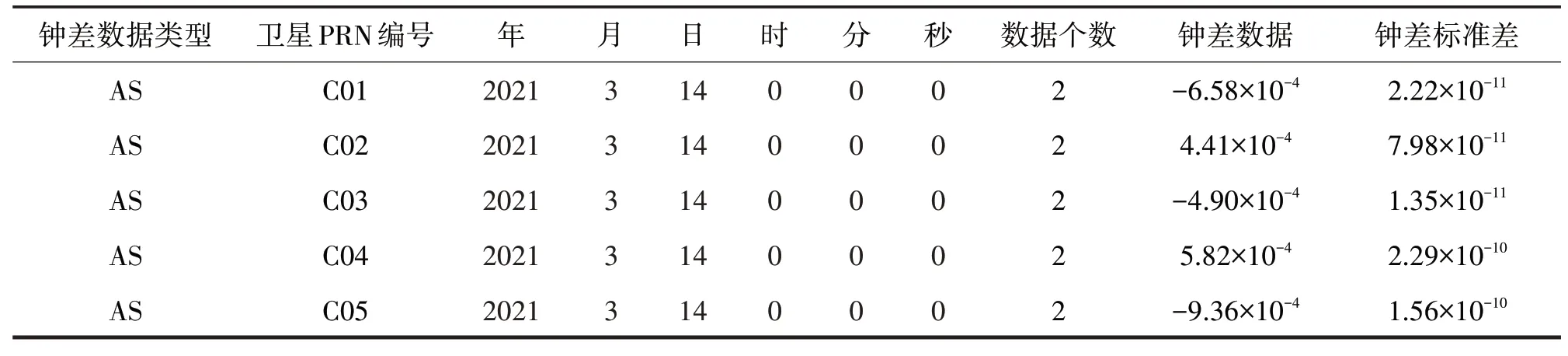
表1 钟差数据文件Tab.1 Data format of iGMAS clock product

本文采用iGMAS提供的2019年12月至2021年2月共13个月北斗卫星的最终钟差数据进行分析，其中2020年7月5日至2020年7月18日的最终钟差（isc）数据缺失，计算时用同时期的快速钟差（isr）数据代替。

北斗卫星导航系统的部分星历如表2所列，使用的iGMAS钟差文件中包含PRN编号为1~40的36颗卫星，包括15颗北斗二号卫星和21颗北斗三号卫星，其中北斗二号卫星与10颗北斗三号卫星使用铷原子钟，11颗北斗三号卫星使用氢原子钟。

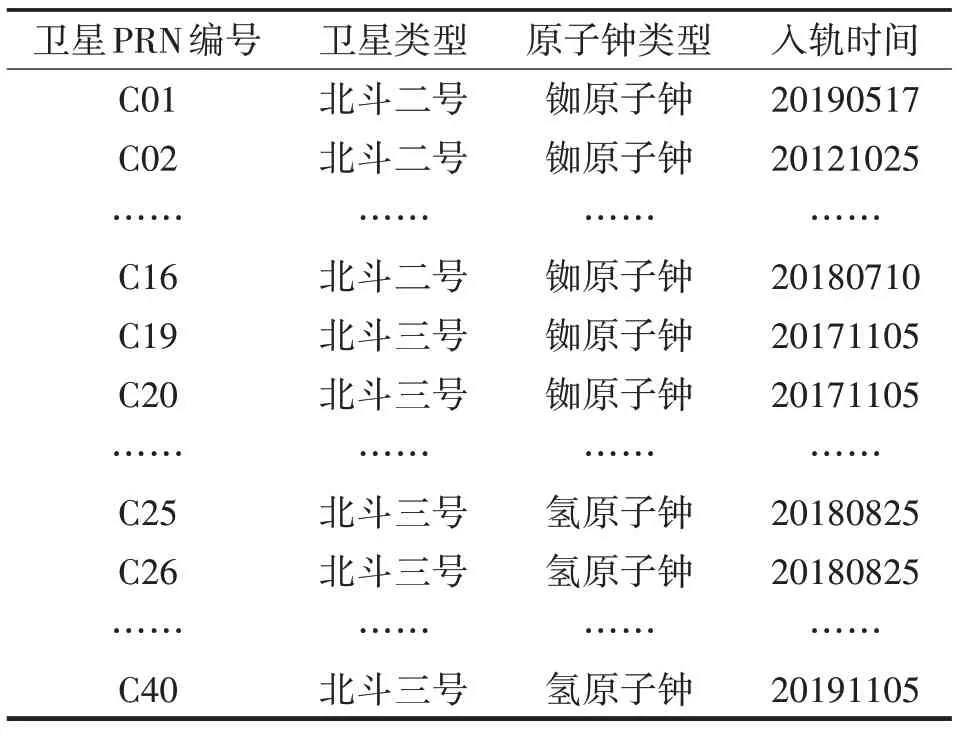
表2 北斗卫星导航系统部分星历Tab.2 Partial constellation information of BeiDou System

2.2 频率准确度评估

本文星载原子钟的频率准确度以月为单位进行评估。必须说明的是，C40卫星由于发射时间较晚，准确度和漂移率评估时并未被纳入，在用于分析计算的数据中，2020年7月5日至2020年7月18日的快速钟差文件中C38和C39钟差数据不全，对它们的准确度与漂移率评估仅利用了17天的数据。

2019年12月至2021年2月期间，北斗二号卫星铷原子钟的频率准确度如图1所示，图中的频率准确度按月平均计算。大部分星载铷钟准确度在±5×10-11范围内，2020年6月后，15台北斗二号卫星铷原子钟的准确度绝对值均保持在1.0×10-10以内。从图1可以看到，铷钟在轨运行时具有较明显的频率漂移，并且多台铷钟频率准确度出现了较大数值的跳变。星载原子钟的频率跳变并不意味着原子钟的状态异常，特别是大幅度或者有规律的频率跳变，通常是系统操作的结果，以保证原子钟的准确度在系统要求的范围内。图中C03和C04卫星的铷钟频率准确度跳变量最大，分别达到1.5×10-10和1.2×10-10；C08、C09、C10、C11和C16频率准确度跳变量级相同，约为4.9×10-11；C01卫星铷钟频率准确度跳变量级较小，约为8.0×10-12；其余卫星的原子钟虽然没有明显的频率调整，但C02、C05和C13等卫星有小于5.0×10-12的频率台阶或变化。

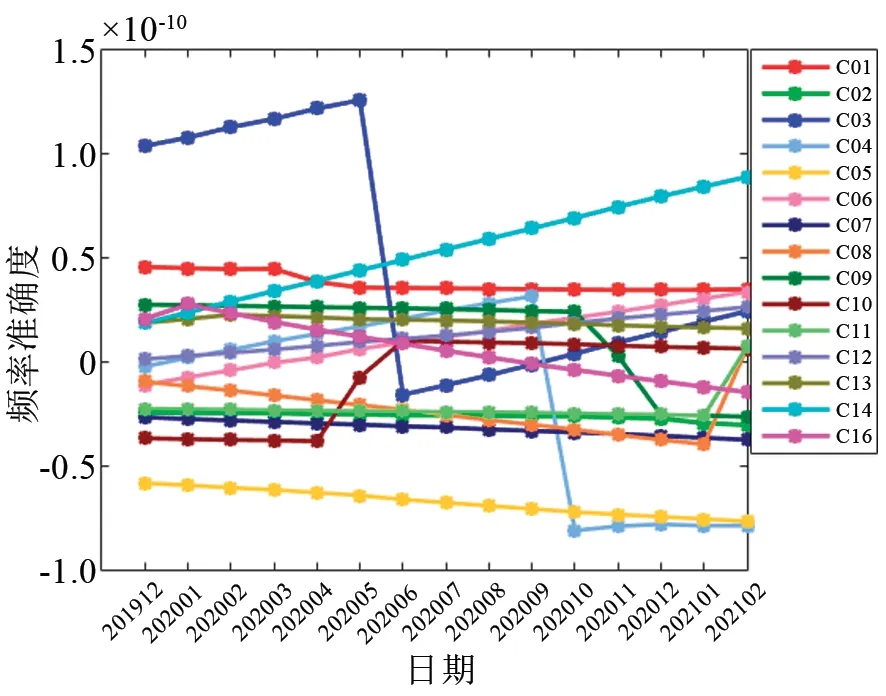
图1 北斗二号卫星铷原子钟准确度Fig.1 Frequency accuracy of BDS-2 RAFS

2019年12月至2021年2月期间，北斗三号卫星铷原子钟的频率准确度如图2所示，准确度均在±7×10-11以内，5台北斗三号卫星铷原子钟的准确度保持在2×10-11以内，另外5台的准确度在2020年8月后也保持在±2×10-11以内。总体来看，北斗三号卫星铷原子钟的频率准确度比北斗二号卫星铷钟的更高。

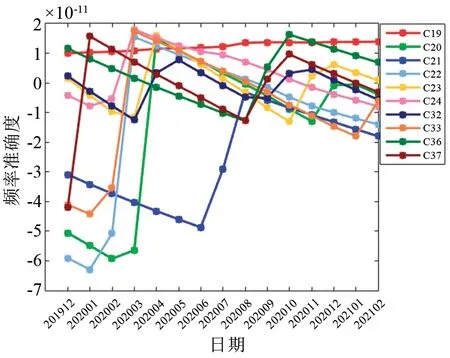
图2 北斗三号卫星铷原子钟准确度Fig.2 Frequency accuracy of BDS-3 RAFS

对比图2和图1的准确度变化曲线可以看到，同时期内北斗三号卫星铷原子钟的频率准确度跳变更频繁，可能的原因包括两个方面：（1）北斗三号铷原子钟的准确度要求更高，增加了频率准确度的调整次数；（2）北斗三号卫星多数为2018年以后发射，铷原子钟运行时间较短，根据铷原子钟输出信号的经验模型，铷原子钟运行初期频率漂移率通常较大，导致频率准确度调整间隔较短，但随着运行时间的增加，铷原子钟频率漂移率会降低并趋于稳定。

2019年12月至2021年2月期间，北斗三号卫星氢原子钟的频率准确度如图3所示。2020年4月后，北斗系统氢原子钟的准确度普遍在±2×10-11以内，且大部分氢原子钟的准确度优于1×10-11。与铷原子钟相比，多台氢原子钟的频率准确度不变，只有C26卫星和C35卫星搭载的氢原子钟出现了频率跳变，量级分别约为2×10-11和5.9×10-11。

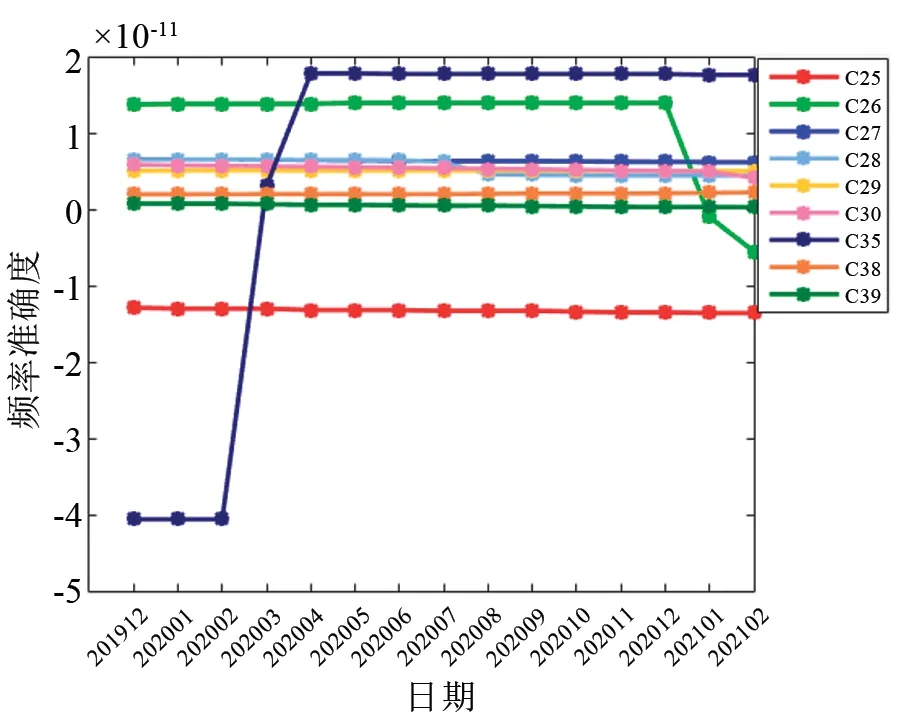
图3 北斗三号卫星氢原子钟准确度Fig.3 Frequency accuracy of BDS-3 PHM

2.3 频率漂移率评估

将钟差数据转换为频差数据后，以月为单位进行天漂移率的计算，若当月出现频率跳动的情况，分别计算频率跳动前后的天漂移率，并按照所占时间比例加权。

图4为北斗二号卫星铷原子钟频率漂移率的统计情况，C01、C02、C07、C09、C10、C11和C13卫星的铷原子钟天漂移率绝对值均小于5×10-14，C05和C12卫星铷钟的天漂移率绝对值在5×10-14左右，其余卫星铷钟的天漂移率绝对值在5×10-14~2×10-13范围内，其中C04和C16卫星铷钟的天漂移率在2020年初较大，绝对值为1.5×10-13左右，但随着时间的推移，这两台铷钟的天漂移率呈明显的下降趋势，于2021年2月分别达到-4×10-14和-9×10-14左右。

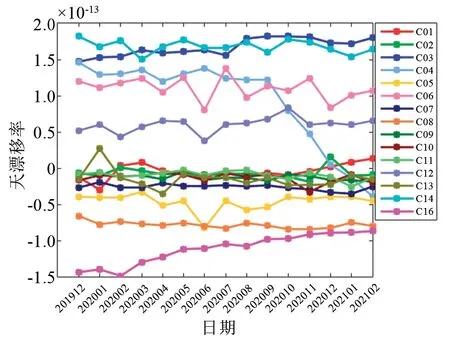
图4 北斗二号卫星铷原子钟频率漂移率Fig.4 Frequency drift of BDS-2 RAFS

2019年12月至2021年2月期间，北斗三号卫星铷原子钟输出频率的天漂移率如图5所示，其中C19卫星铷钟的漂移率很小，达到10-15量级，其余铷原子钟的天漂移率大多在10-13量级，但这些铷原子钟的天漂移率明显呈减小趋势，到2021年2月时已有5台铷原子钟的天漂移率进入10-14量级，这与GPS铷钟天漂移率变化的经典模型趋势一致[10]。

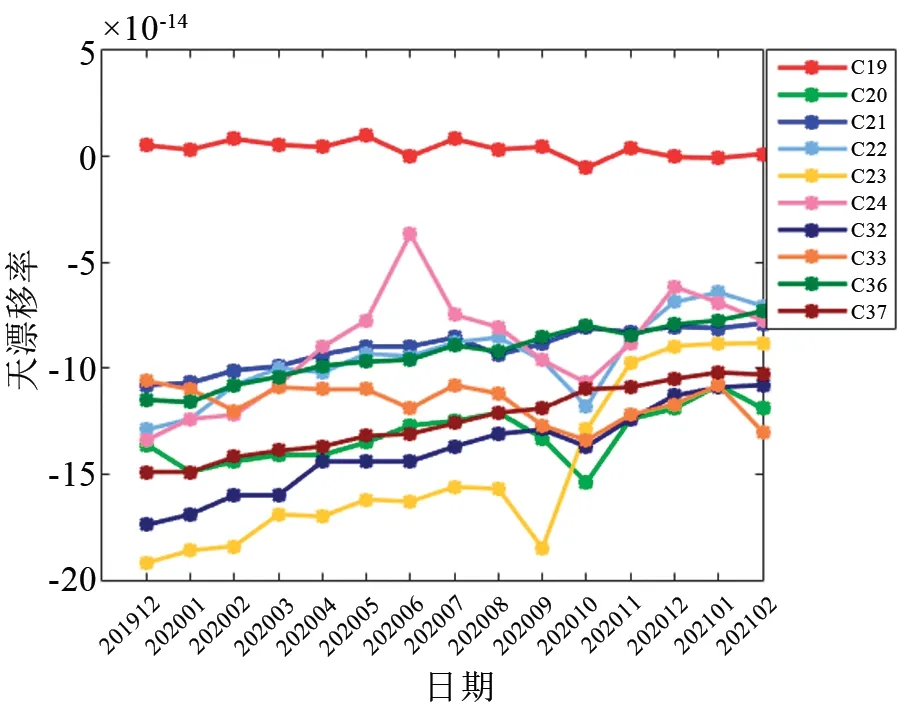
图5 北斗三号卫星铷原子钟频率漂移率Fig.5 Frequency drift of BDS-3 RAFS

图6为北斗三号卫星氢原子钟天漂移率的计算统计情况。

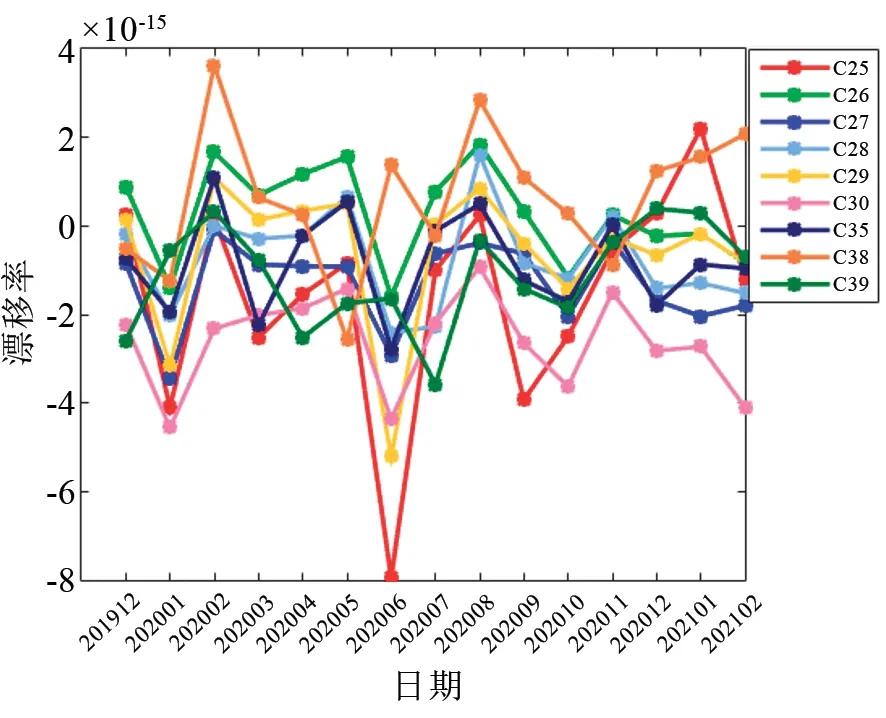
图6 北斗三号卫星氢原子钟天漂移率Fig.6 Frequency drift of BDS-3 PHM

由图6可以看出，所有氢原子钟的天漂移率绝对值均达到10-15量级，且大部分时间能够达到5×10-15以内，多台氢原子钟的天漂移率甚至达到10-16量级。另外，虽然氢原子钟的漂移率仍有波动，但是多数氢原子钟的天漂移率波动趋势比较一致，如2020年1月、2020年6月 和2020年10月 多台氢原子钟出现了天漂移率负向增加的情况，可能与其他原因引入的噪声有关。对比能够看出，北斗系统氢原子钟的天漂移率明显小于铷原子钟。

2.4 频率稳定度评估

根据2.2节对原子钟频率准确度的分析，导航原子钟的输出频率存在跳变和波动，并且无法根据钟差数据直接判断异常波动是来自于原子钟自身、地面控制段的控制命令还是钟差测量系统。为了更好地评估原子钟的频率稳定度，本文选取连续100天无异常波动和频率跳动的数据进行稳定度计算，其中铷原子钟采用哈达玛方差计算，氢原子钟采用阿伦方差计算。由于iGMAS钟差数据的时间间隔为300 s，稳定度评估从300 s开始。

北斗二号卫星铷原子钟稳定度趋势如图7所示，9 600 s以前稳定度曲线的斜率整体为τ-1/2，即输出信号噪声以铷原子钟的调频白噪声为主。C06卫星铷原子钟的稳定度在10 000 s以后开始变差，天稳定度约1×10-13，主要原因是该星原子钟的准确度在评估时间内存在一定波动，其余铷原子钟的稳定度趋势基本一致，300 s的稳定度普遍在1×10-13~5×10-13范围内，10 000 s稳定度在1×10-13~5×10-13范围内，天稳定度在1×10-14~5×10-14范围内。

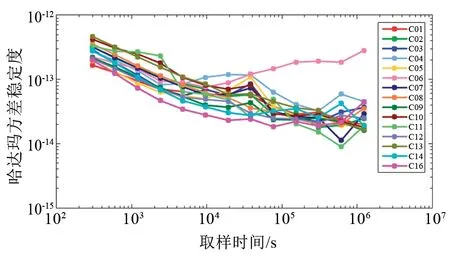
图7 北斗二号卫星铷原子钟稳定度Fig.7 Frequency stability of BDS-2 RAFS

北斗三号卫星铷原子钟的频率稳定度如图8所示。10台铷原子钟的稳定度一致性较好，4 800 s之前的稳定度曲线斜率整体为τ-1/2，3 00 s稳定度优于2×10-13，其中C23卫星铷钟的300 s稳定度最好，达到1×10-13，所有北斗三号卫星铷原子钟10 000 s左右的稳定度均优于4×10-14，天稳定度均优于3×10-14。

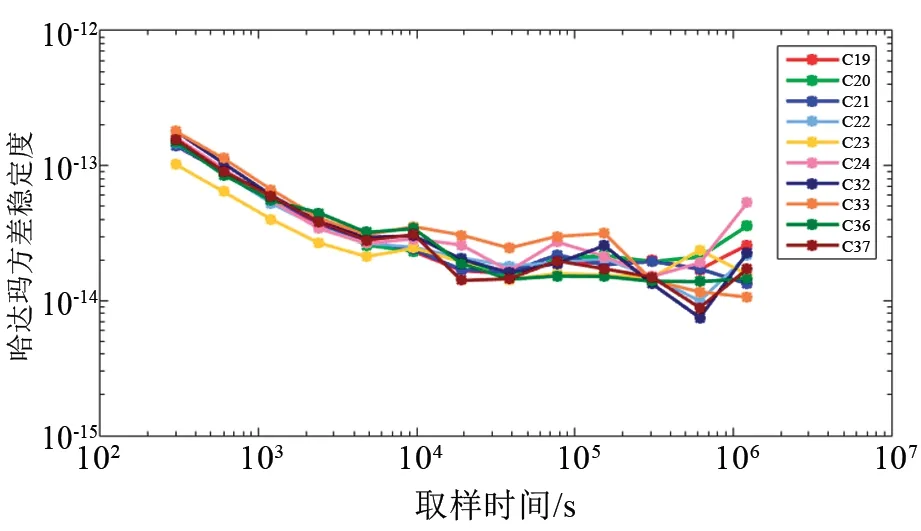
图8 北斗三号卫星铷原子钟频率稳定度Fig.8 Frequency stability of BDS-3 RAFS

北斗三号卫星氢原子钟的稳定度如图9所示，5 000 s之前的稳定度曲线斜率整体为τ-1/2，300 s稳定度优于2×10-13，其中C34和C40卫星氢原子钟的300 s稳定度最好，优于1×10-13，北斗卫星氢原子钟的指标一致性较好，且长期稳定性能优异，10 000 s左右的稳定度为1×10-14~3×10-14，所有氢原子钟的天稳定度均优于3×10-14，并且随着时间常数的增加，仍呈下降趋势。

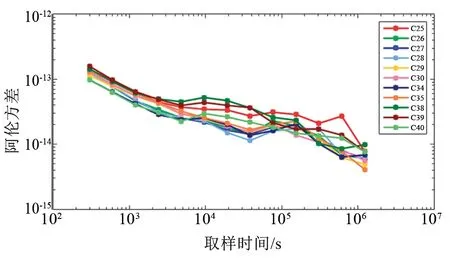
图9 北斗三号卫星氢原子钟频率稳定度Fig.9 Frequency stability of BDS-3 PHM

北斗二号卫星铷原子钟、北斗三号卫星铷原子钟和氢原子钟的稳定度分别平均后的数据如图10所示，计算时剔除了北斗二号卫星铷原子钟存在波动的C06，北斗三号卫星氢原子钟的C25、C38和C39。对比可见，北斗三号卫星铷原子钟和氢原子钟的稳定度明显高于北斗二号卫星铷原子钟的稳定度。取样时间在1天之内时，北斗三号卫星铷原子钟的稳定度与氢原子钟的稳定度指标相近，随着取样时间的增加，氢原子钟的稳定度优于铷原子钟的稳定度，达到10-15量级。

图10 北斗导航卫星原子钟平均稳定度Fig.10 Frequency stability comparison of BDS atomic frequency standard

3 总结

北斗卫星导航系统的原子钟包括铷原子钟和氢原子钟，其中北斗二号卫星使用铷原子钟，北斗三号卫星使用性能更好的铷原子钟和氢原子钟，本文利用iGMAS提供的2019年12月至2021年2月的最终钟差数据，对北斗导航卫星原子钟的性能进行了评估，结果表明，北斗三号卫星使用的原子钟比北斗二号的性能明显提升，其中氢原子钟的长期性能更好，10天稳定度和天漂移率普遍达到10-15量级。星载原子钟性能的提升能够有效改善卫星导航定位精度。未来随着更高精度原子钟的开发应用，卫星导航定位的精度将会进一步提升。需要说明的是，本文对iGMAS钟差数据转换得到的原子钟准确度数据仅进行了必要的粗差剔除并未做进一步的优化处理，考虑到钟差数据本身包含评估噪声，因此作者认为，北斗原子钟实际稳定度性能优于本文评估的结果。

致谢

感谢iGMAS提供的卫星钟差产品。