不同导星数量和排布情况下地表层自适应光学系统的性能分析

赵梓旭,马晓燠,饶长辉

(1 中国科学院大学,北京 100049;2 中国科学院自适应光学重点实验室,四川 成都 610209;3 中国科学院光电技术研究所,四川 成都 610209)

0 引言

自适应光学(AO)是解决大气湍流对于天文观测影响的一项最具有应用前景的技术。传统AO采用单一波前传感器对由大气湍流引起的波前畸变进行探测,由于受到大气非等晕性的影响,往往存在校正视场(FOV)小的问题。随着研究的深入进行,发现大部分的湍流扰动都集中在了地面。在此基础上,Rigaut在2000年提出了地表层自适应光学(GLAO)的概念[1]。GLAO通过多个导星(LGS)和波前探测器对大气湍流引成的波前畸变进行探测,并由一个波前校正器来抵消地表层湍流的影响,从而可以在较大视场范围内提高望远镜的观测能力。由于GLAO出色的校正性能和应用前景,逐渐成为大口径太阳望远镜的标配,因此,对GLAO系统的性能进行科学评价与分析具有重要意义。

近年来,国内外多家研究机构都对GLAO展开了深入研究和实验。欧洲南方天文台利用其MAD实验平台,开展了GLAO系统的数值仿真实验和天文观测实验,实验结果表明,GLAO系统在观测视场中心性能最好,校正视场可达到2′[2];Rimmele等[3]基于DST研发了一套太阳GLAO系统,由于当时实验中使用的夏克-哈特曼波前传感器的采样精度限制,这套太阳GLAO系统并没有发挥出良好的校正性能;美国加州州立大学北岭分校的Ren等[4]对比了太阳GLAO系统的两种波前传感方法,一种为采用4颗离散导星进行波前探测,其中一颗在中心,三颗在周围呈均匀排布;第二种选用太阳黑子作为一个大的连续导星区域进行波前探测,通过系统性能分析发现,当探测目标在中心零视场周围时,采用第二种波前探测的系统性能更好,当探测视场较大时,两种波前探测方式的性能相当;美国亚利桑那大学的Baranec等[5]也开展过开环GLAO实验,实验发现校正后的图像半高全宽(FWHM)约为校正前的1/3。美国的Hart等[6]在H波段进行GLAO的闭环校正实验,通过计算可以得出,经GLAO系统校正后,FWHM由1.07′′下降到0.2′′。1.8 m口径中国大型太阳望远镜(CLST)在首光观测中,得到了经GLAO校正后的三波段成像,结果表明,GLAO系统显著提高了图像质量[7]。

在国家自然科学基金支持下,中国科学院光电技术研究所太阳自适应光学项目组正在为云南天文台一米新真空太阳望远镜(NVST)研制一套多层共轭自适应光学(MCAO)系统,该系统包括一套独立工作的高阶GLAO。基于空间频谱滤波理论,本文利用GLAO系统滤波器模型,使用NVST相关参数和经典大气湍流分层模型,针对系统中不同导星数量与排布方式,对GLAO系统的性能进行分析与评价,从而对导星数量与排布进行优化。

1 GLAO系统模型

1.1 点扩散函数计算流程

使用远场长曝光点扩散函数(PSF)的FWHM来衡量GLAO系统的校正效果,在此模型中,将PSF的FWHM作为系统性能的评价指标。

光波从无穷远处传至望远镜时,穿过大气湍流,受到了一定程度的扰动,此时望远镜系统的长曝光光学传递函数(OTF)的关系式为

式中T0(k)与望远镜有关,表示此望远镜达到衍射极限时所对应的光学传递函数,(λk)表示在望远镜瞳面范围内的相位结构函数。

OTF与PSF为一对傅里叶变换对,在已知其中一个函数的条件下,可以通过傅里叶变换与反变换求得另一个函数的表达式。因此,由OTF即可求得PSF的表达式,进而计算PSF的FWHM,评价系统性能[8]。

将相位残差ε(x)理解为经过空间滤波的大气相位,该空间滤波器的具体形式取决于自适应光学系统的类型和具体参数。在此引入一个乘数G(f),f为频域单位,将残留相位功率谱与大气相位功率谱联系起来。利用大气相位功率谱与G(f)来表达残留相位功率谱,表达式为

式中|G(f)|2即为“误差传递函数(ETF)”,它描述了系统未校正的残余大气光谱部分。

根据大气分层理论,大气湍流可以等效为任意数量的薄湍流层组合,ETF也可以进行逐层计算。由于各层在统计上彼此不相关,因此得到的功率谱W(f)是所有层的功率谱之和。第i个湍流层的相位功率谱为

式中r0,i表示每层湍流的大气相干长度,r0,i-5/3=0.423(2π/λ)Ji,Ji=C2ndh表示每层的湍流强度。

在相位结构函数的表达式中,J和成像波长λ作为乘数因子输入。令r0,i=1,计算每一层“归一化”后的残留相位结构函数,计算公式为

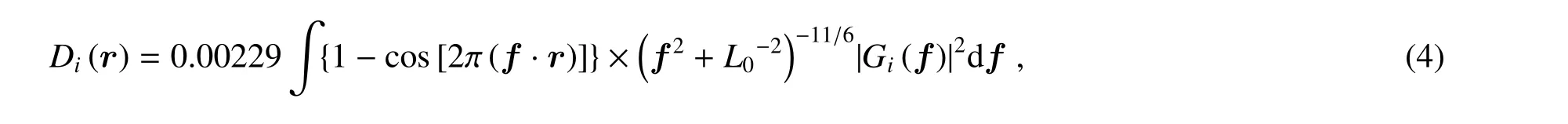
每一层的影响按照每层的湍流强度Ji进行缩放并求和,得到最终的残留相位结构函数,即

计算流程图如图1所示。

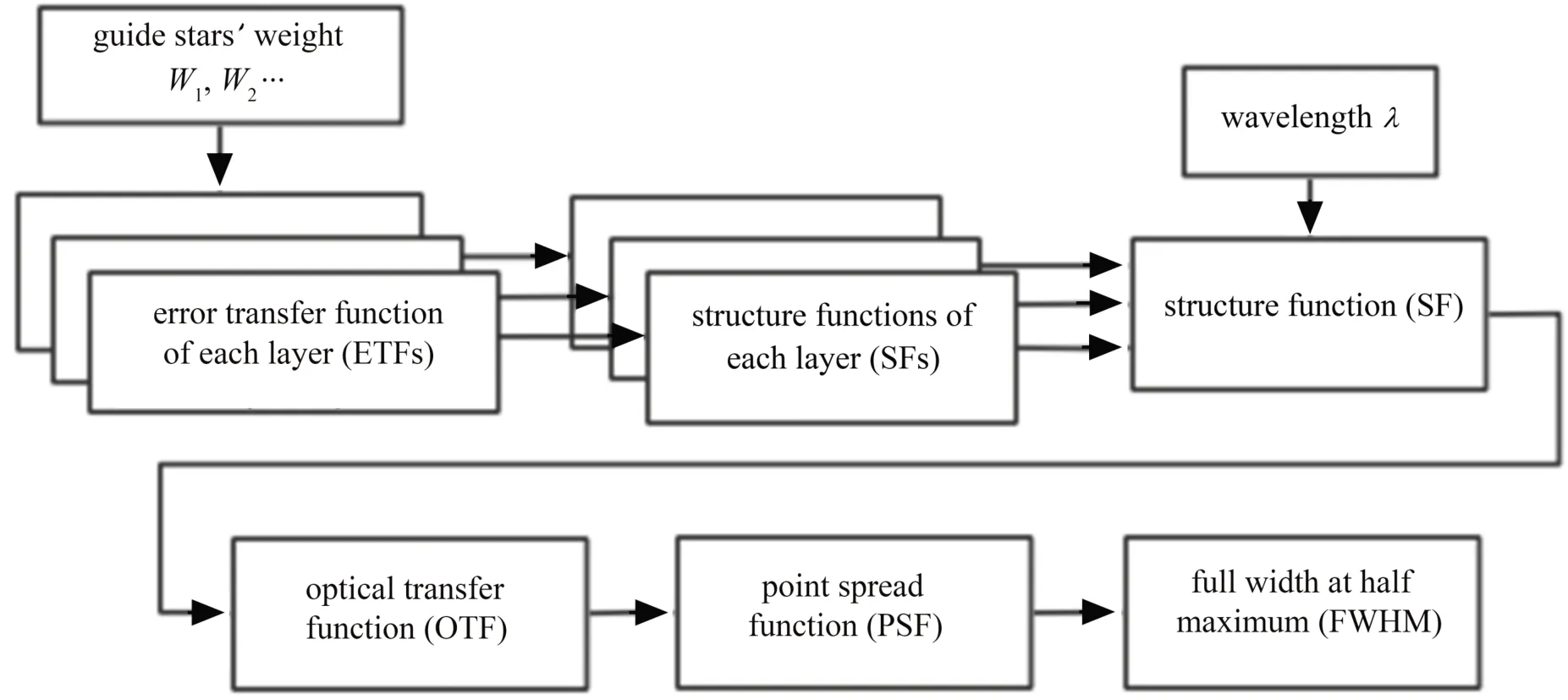
图1 GLAO系统点扩散函数计算流程图Fig.1 Flow chart of point spread function calculation in GLAO system

1.2 多导星GLAO系统误差传递函数

根据地表层自适应光学技术基本理论,假设高于变形镜共轭水平高度h处仅有一个薄的湍流层,即为地表层湍流。导星的高度为H,设a是从孔径中心观察的信标与物体之间的角度,x是孔径平面中的坐标矢量,示意图如图2所示。由图中所示的几何形状可得出,从孔中的点x看,物体和信标波前的相对位移b为

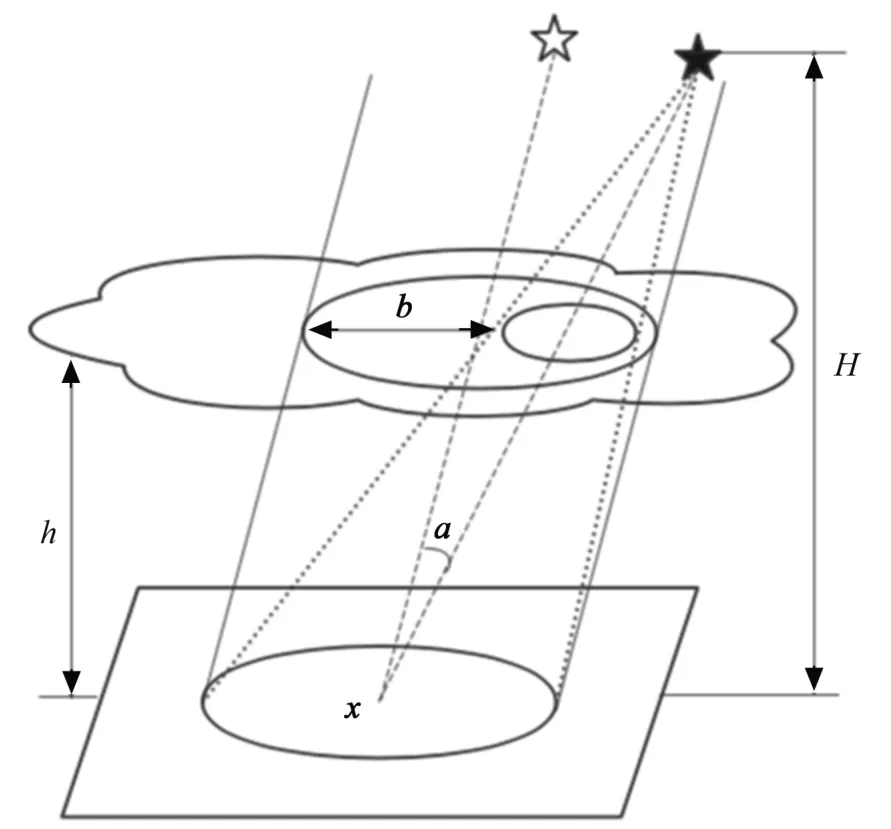
图2 误差传递函数推导几何模型Fig.2 Derivation of geometric model from error transfer function

从无限远目标传至望远镜的光束可看成是圆柱体,信标传至望远镜的光束是圆锥体,因此,在湍流层的采样区域上,由信标采样的区域直径比实际目标采样的区域直径小γ倍,即激光导星探测到的像差比来自物体的像差减少了γ倍。它通过减小补偿相位幅度取代空间“拉伸”。γ的计算公式为

补偿相位是通过将大气相位偏移b通过的空间响应进行卷积得出的。为了处理不同信标的情况,Tokovinin[9]引入了“信标类型(BS)”因子,该因子描述了信标在天空上的角度分布。相应的空间滤波器为

式中低通空间滤波器R(f)描述了波前校正器的有限分辨率,在此忽略由波前校正器所引入的校正误差,令R(f)=1;S表示BS因子,当只有一个信标时,S=1,有多个信标时,假设共有K个信标,第k个信标的位置为ak,权重为wk,并且=1,此时S(k)的表达式为

残余相位功率谱是整体大气相位功率谱和误差传递函数|G(f,x)|2的乘积。|G(f,x)|2描述了系统未校正的残余大气光谱的一部分,G(f,x)可以由滤波器X(f,x)得到,表达式为

在望远镜口径区域D内对x进行平均,引入艾里函数,艾里函数的表达式为

最后得到多导星GLAO系统的ETF表达式为

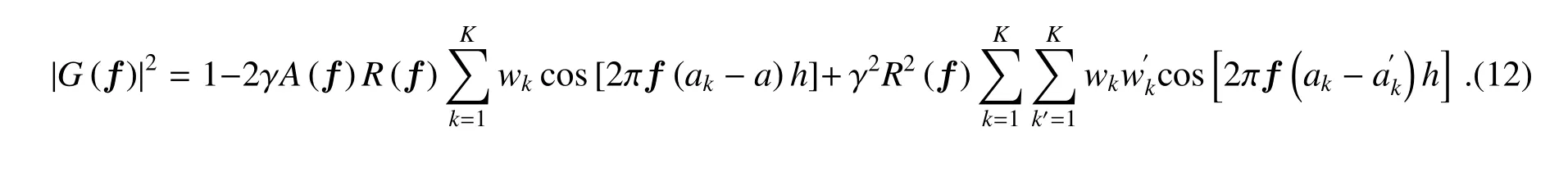
2 导星数量与排布优化

NVST[10]由中国科学院云南天文台研制,望远镜坐落于抚仙湖太阳观测站。NVST于2010年成功首光,并一直进行太阳观测,是我国进行太阳观测和太阳物理研究的重要利器和主力军。为了使仿真实验结果更加具有普适性,在仿真实验中,使用典型的大气湍流7层模型,此模型为根据Cerro Pachon站址数据拟合而成的大气湍流模型[11],模型中将大气湍流等效为7层,每层大气湍流的高度和权重占比如表1所示。湍流等效γ0为10 cm[12]。

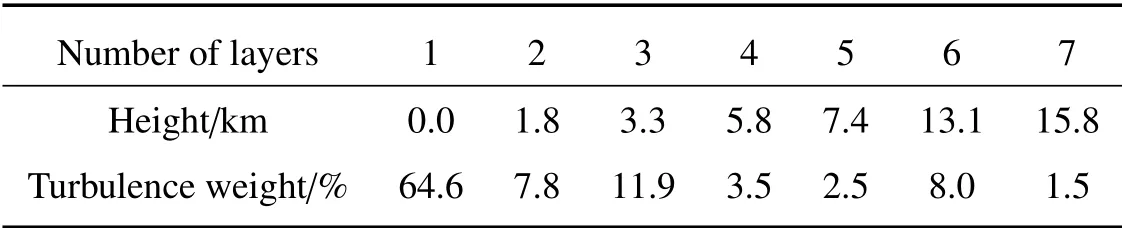
表1 Cerro Pachon-7层大气湍流模型Table 1 Cerro Pachon-7 layer atmospheric turbulence model

根据NVST相关技术参数,望远镜口径为0.98 m,探测波长为0.589 m,探测视场为2′,结合上述经典湍流模型,忽略波前传感器探测误差和变形镜校正误差,通过调整系统中导星的数量与排布方式,使GLAO系统校正性能提高。仿真实验中,在中心零视场至最大视场边缘共选取41个不同的视场,在同一视场下选取8个方向的目标,分别计算目标位置PSF的FWHM,取平均值作为此视场下的FWHM值;在太阳GLAO系统中,导星类型为自然导星。

2.1 导星数量优化

首先探究系统的导星数量优化,分别设置4、5、6、8、10颗导星,均设置最大探测视场边缘,呈均匀的环形排布,导星位置分布如图3所示。

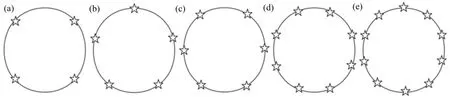
图3 导星呈均匀环形分布位置示意图。(a)4 LGSs;(b)5 LGSs;(c)6 LGSs;(d)8 LGSs;(e)10 LGSsFig.3 The position diagram of guide star in uniform circular distribution.(a)4 LGSs;(b)5 LGSs;(c)6 LGSs;(d)8 LGSs;(e)10 LGSs

图4显示了导星数量不同时GLAO系统的性能变化。由图可知,随着导星数量的增多,系统PSF的FWHM变小。对于GLAO来说,在视场范围内,导星数量越多,在目标视线上带回有效波前信息越多,高层湍流信息会在平均的作用下被过滤得更好,地表层湍流重构更准确,因此校正效果更好,图4也验证了导星数量对系统性能提高的作用。同时,导星数量也直接关系到波前复原的计算复杂度和系统带宽,并不是数量越多越好,8颗导星相比6颗导星,FWHM最大下降不到0.04′′,故6颗导星下系统性能得到了显著改善。

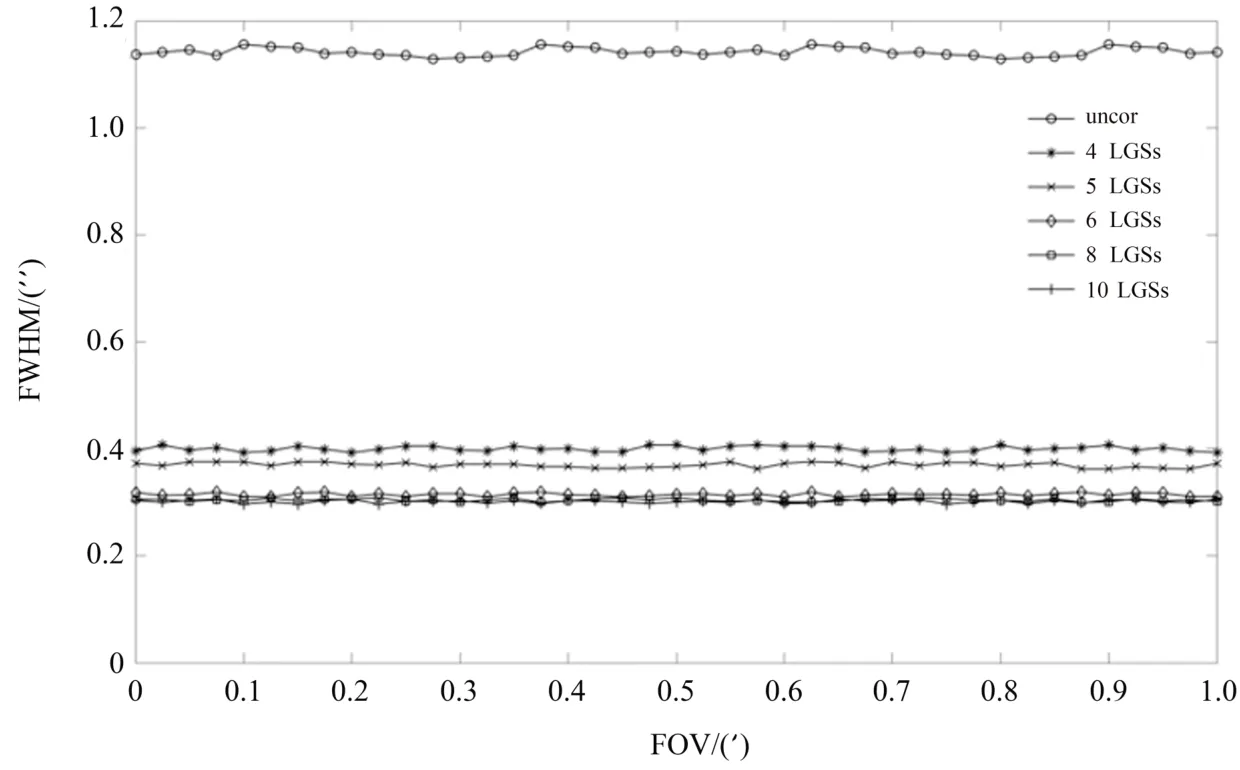
图4 NVST不同导星数量GLAO性能对比Fig.4 Comparison of GLAO performance of NVST with different number of guide stars

2.2 导星位置优化

令6颗导星呈均匀的正多边形环形排布,调整导星位置,分别设置在视场中心与最大视场边缘之间的3/4、1/2、1/4处,导星位置分布如图5所示。

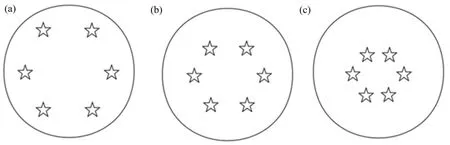
图5 导星呈均匀分布向中心靠拢位置示意图。(a)3/4处;(b)1/2处;(c)1/4处Fig.5 The position diagram of guide stars which are evenly distributed to the center close position.(a)3/4 position;(b)1/2 position;(c)1/4 position

图6 显示了随着导星位置的不同GLAO系统的性能变化。由图可以发现,当导星数量一定,导星位置不断向视场中心靠拢,零视场的FWHM不断减小,但是最大视场角边缘的FWHM不断增大。表2给出了在视场范围内导星不同位置分布的FWHM平均值,6颗导星均匀排布在视场中心与最大视场边缘之间3/4处时,系统整体的校正效果较好。

表2 6颗导星位置不同系统FWHM平均值Table 2 FWHM mean value of the system with different position of 6 guide stars

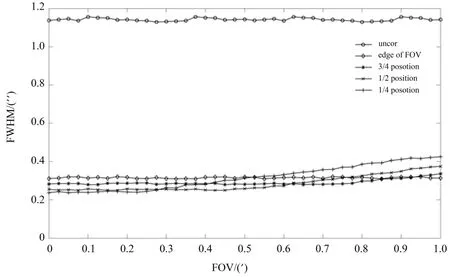
图6 NVST导星位置变化GLAO性能对比Fig.6 Performance comparison of GLAO with position change of NVST guide stars

2.3 导星排布方式优化

继续改变导星排布方式,设置4、5、6、8、10颗导星。其中,均在零视场处设置1颗导星,其余导星在最大探测视场边缘呈均匀的环形排布,导星位置分布如图7所示。

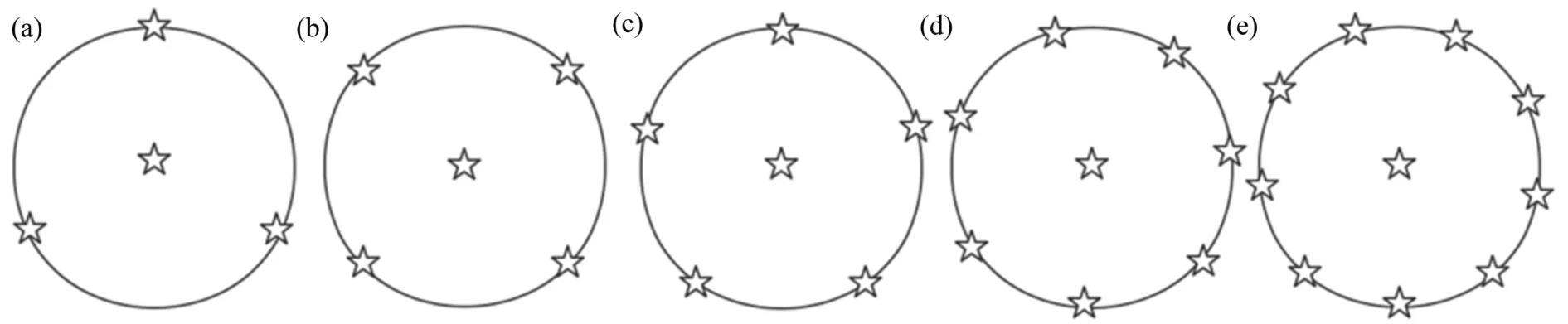
图7 导星呈中心1颗其余均匀分布位置示意图。(a)4 LGSs;(b)5 LGSs;(c)6 LGSs;(d)8 LGSs;(e)10 LGSsFig.7 The position diagram of guide stars with one in the center and the rest evenly distributed.(a)4 LGSs;(b)5 LGSs;(c)6 LGSs;(d)8 LGSs;(e)10 LGSs

图8 (a)显示了不同数目的导星在这种排布方式下GLAO系统的性能变化。以6颗导星为例,图8(b)显示了两种排布下系统校正性能对比。由图可以发现,中心有1颗导星的排布方式和全部均匀环形排布方式相比,中心零视场的校正效果会有所提升,但最大视场边缘会有略微下降。在视场范围内两种排布的FWHM平均值如表3所示,6颗导星呈中心有1颗导星、其余导星均匀分布的排布方式时,系统整体的校正效果较优。

表3 6颗导星排布方式不同系统FWHM平均值Table 3 Average FWHM of 6 guide stars in different systems

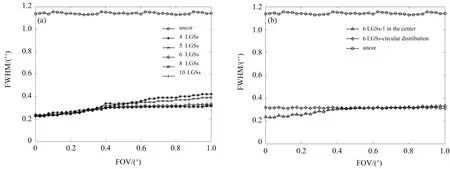
图8 GLAO性能。(a)非均匀排布下不同导星数量;(b)6颗导星两种排布方式Fig.8 GLAO performance.(a)Different guide star number under non-uniform arrangement;(b)two arrangements of six guide stars

3 结论

根据GLAO系统模型,调整导星数量与排布,对NVST上GLAO系统进行性能分析,可知:6颗导星在环形分布情况下,地表层自适应光学系统校正性能较优;调整导星位置,令6颗导星呈均匀环形分布并不断向中心靠拢时,当6颗导星均匀排布在视场中心与最大视场边缘之间3/4处时,系统整体的校正效果较好;调整导星排布方式,采用中心1颗导星、其余导星在视场边缘呈均匀环形分布方式时,系统校正效果更佳。研究结果对项目组正在研制的一米新真空太阳望远镜地表层自适应光学系统具有重要指导作用和参考价值。

致谢:感谢中国科学院光电技术研究所的张兰强副研究员和钟立波副研究员对本文的帮助和指导。