基于主成分分析的RBF神经网络预测SO2浓度
2022-10-13张琦锦郭映映李素文牟福生
张琦锦,郭映映,李素文*,牟福生*
(1 淮北师范大学物理与电子信息学院,安徽 淮北 235000;2 污染物敏感材料与环境修复安徽省重点实验室,安徽 淮北 235000)
0 引言
随着国家工业化发展,排放的污染气体对空气质量和气候变化都产生了重要影响。SO2是大气中常见的痕量气体,不仅危害人体健康,而且对酸雨形成、生态环境也有巨大影响[1-3]。因此预测SO2浓度变化趋势的研究对国家政府制定污染预防和控制等相关政策具有重要意义[4-5]。
近年来,污染气体预测建模方面的研究已成为国内外研究的热点。国际上Park等[6]利用长短时记忆神经网络实现了颗粒物浓度的估算,Luna等[7]在神经网络的基础上利用向量机研究了大气层O3浓度。国内陈柳等[8]在反向传播(BP)神经网络模型的基础上结合小波分析预测SO2浓度变化趋势,黄鸿等[9]基于深度学习和极限学习对大气中SO2浓度进行了预测,司志娟等[10]利用灰色径向基(RBF)神经网络预测了空气质量指数变化趋势。传统的神经网络预测模型具有收敛速度快、分类能力好、搜索能力强等优点。但是传统的网络模型偏向于用线性回归算法筛选数据,忽略了无关线性参数的影响,使得预测过程中产生数据病态的现象,降低了预测结果的准确性。而主成分分析(PCA)算法是对多种变量进行成分降维的统计方法[11]。因此,本文结合PCA算法和RBF神经网络,构建了PCA-RBF预测模型,利用该模型对北京大兴地区某天的SO2浓度值进行预测并保留,将其作为下一天预测模型的输入参数。以此不断地将预测浓度值向前延伸并进行连续的预测和分析,从而实现SO2浓度值的滚动预测。
1 网络模型构建
1.1 PCA算法
PCA核心思想就是通过借助正交变换求解输入变量的相关矩阵,并根据相关矩阵对应的特征值得到累计方差贡献率,从而得到原变量的主成分参数,这些参数能概括还原输入变量原有的信息[12]。本研究利用PCA算法对输入的气象数据进行成分降维,将求解的成分按照特征值的大小排序,得出气象参数的累计贡献率。按照累计贡献率高于80%的原则,对气象参数进行成分划分,将SO2同组成分参量作为预测模型的输入样本,以减少无关参量的影响,提高模型预测精度,并减少模型运行时间。
1.2 PCA-RBF网络构建
PCA-RBF神经网络分为输入、隐含和输出三层(图1),各层中包含多个神经节点,同层神经节点之间不存在连接,只有相邻层次的神经节点相互连接,其基础是隐含层内部空间的基[13]。PCA-RBF网络模型过程如下:
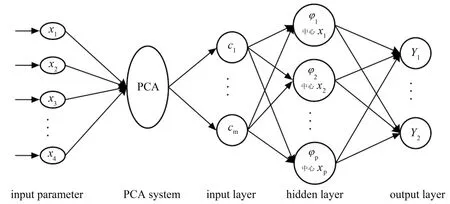
图1 PCA-RBF网络模型结构图Fig.1 PCA-RBF network model architecture
1)PCA对输入的参数进行成分降维,并求解输入气象数据的相关矩阵、特征值和累计贡献率。
2)对气象参数进行成分划分,保留SO2同组成分的气象参数,作为网络输入样本。
3)神经网络对输入气象参数进行归纳分组,确定模型内部基的中心向量。
4)输入层将样本映射到隐空间,隐含层把接收的信号进行模式转换,改变信号的线性状态,得到输出结果,即模型内部基的激活函数φi,其计算公式为

式中x表示输入气象数据,ai表示模型内部基的中心向量,bi表示模型内部基的宽度,n表示隐含层神经节点的个数。
5)求解模型权值,对隐藏层输出信号进行加权变化。权值w的求解公式为
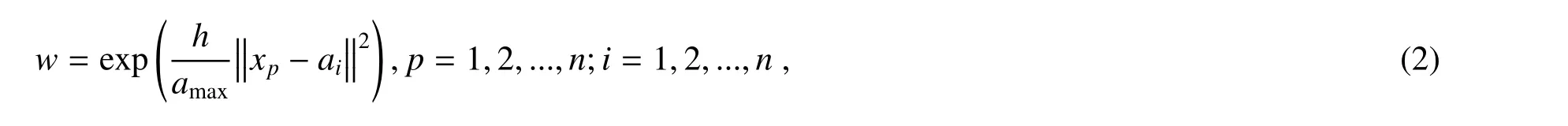
式中h表示中心向量的数目,amax表示中心的最大值,xp表示第p个输入样本。
6)对输入的数据权值加权,输出层输出结果,结束学习。
2 数据分析
2.1 数据来源与预处理
以北京大兴地区SO2浓度为研究目标,选取的时间段是2019年9月1日至2020年10月31日。实验数据来源于中国气象数据网,网络模型的输入数据包括气象参数(降水量、平均水气压、日照时数、气压最值、气温最值、最小相对湿度、最大风速和最大风速的风向等)和空气质量参数(NO2、PM2.5、PM10、SO2、CO和O3),采用均值法补全丢失的数据[14]。
2.2 逐步回归法筛选数据
数据中不同气象参数对神经网络预测SO2浓度的影响存在差异,为消除无关参数对预测结果的影响,通过逐步回归方法筛选出与SO2呈相关性的气象因子,具体结果如表1所示。表中皮尔逊相关性系数的正负仅示意正负相关,其绝对值越接近1,相关性就越好。参量中NO2的皮尔逊系数值为0.636,表明NO2与SO2相关性最高,最大风速风向的皮尔逊系数值为0.07,表明最大风速的风向与SO2相关性最低。通过逐步回归分析模型的处理,与SO2在0.01显著水平下呈正相关的参数有5个(气温最低值、NO2、CO、PM10、PM2.5);与SO2在0.01显著水平下呈负相关的参数有5个(O3、极大风速、气压最低值、气温最高值、最小相对湿度);与SO2在0.05显著水平下呈负相关的参数仅1个(最大风速的风向)。
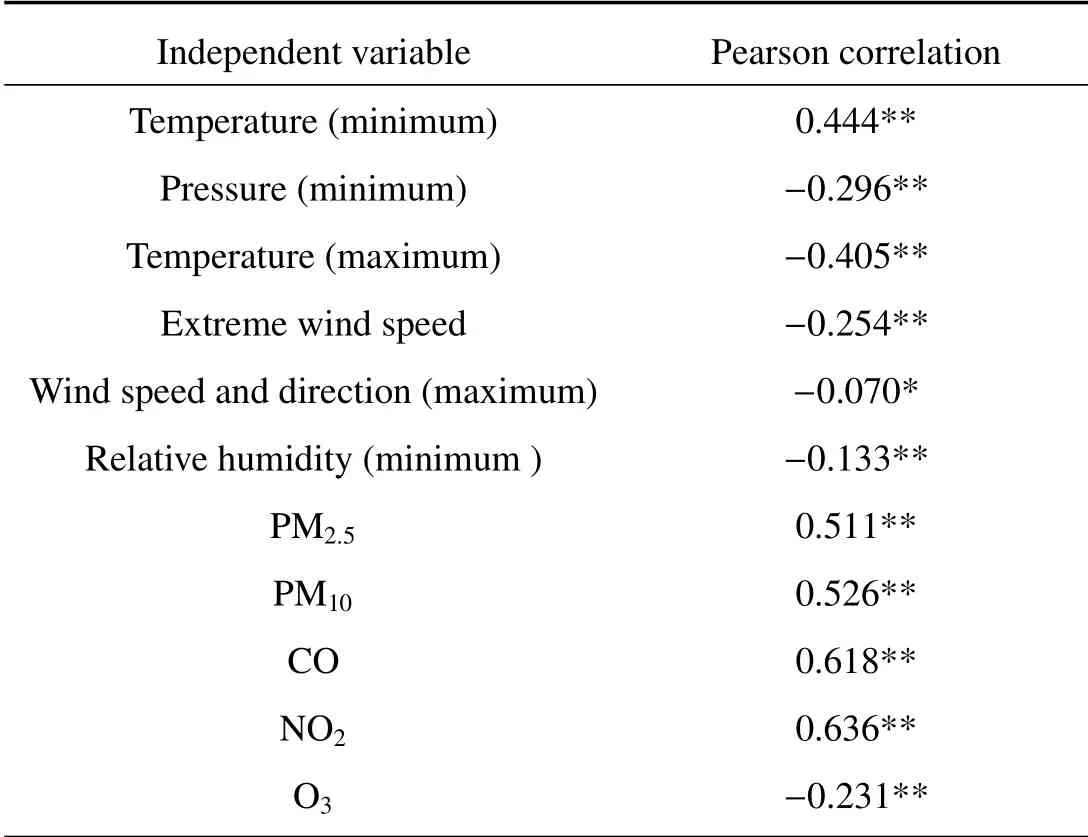
表1 SO2与气象参数逐步回归分析Table 1 Stepwise regression analysis between SO2 and meteorological parameters
2.3 主成分分析筛选数据
将经过逐步回归分析筛选的输入数据划分为两部分:训练神经网络数据和测试神经网络结果数据。其中以2020年10月气象参数作为测试数据,其余时间段的气象参数作为训练集输入到预测模型[15]。气象数据中大数值数据会导致小数值数据的影响被忽略,所以对各种气象数据进行归一化处理,使得气象数据的数值范围控制在0~1内[16]。气象参数归一化后的数值mi的计算公式为

式中ni为气象数据的输入数值。
应用matlab对归一化后的气象参数进行主成分降维,根据相关矩阵得到对应特征值和累计方差贡献率,如表2所示。表中前四种主成分的累计贡献率是80.44%,按照标准80%的原则,前四个主成分可作为基础成分代替原有数据。因此经PCA筛选的参数分为四个主成分,这四个主成分能概括还原输入参数的信息。
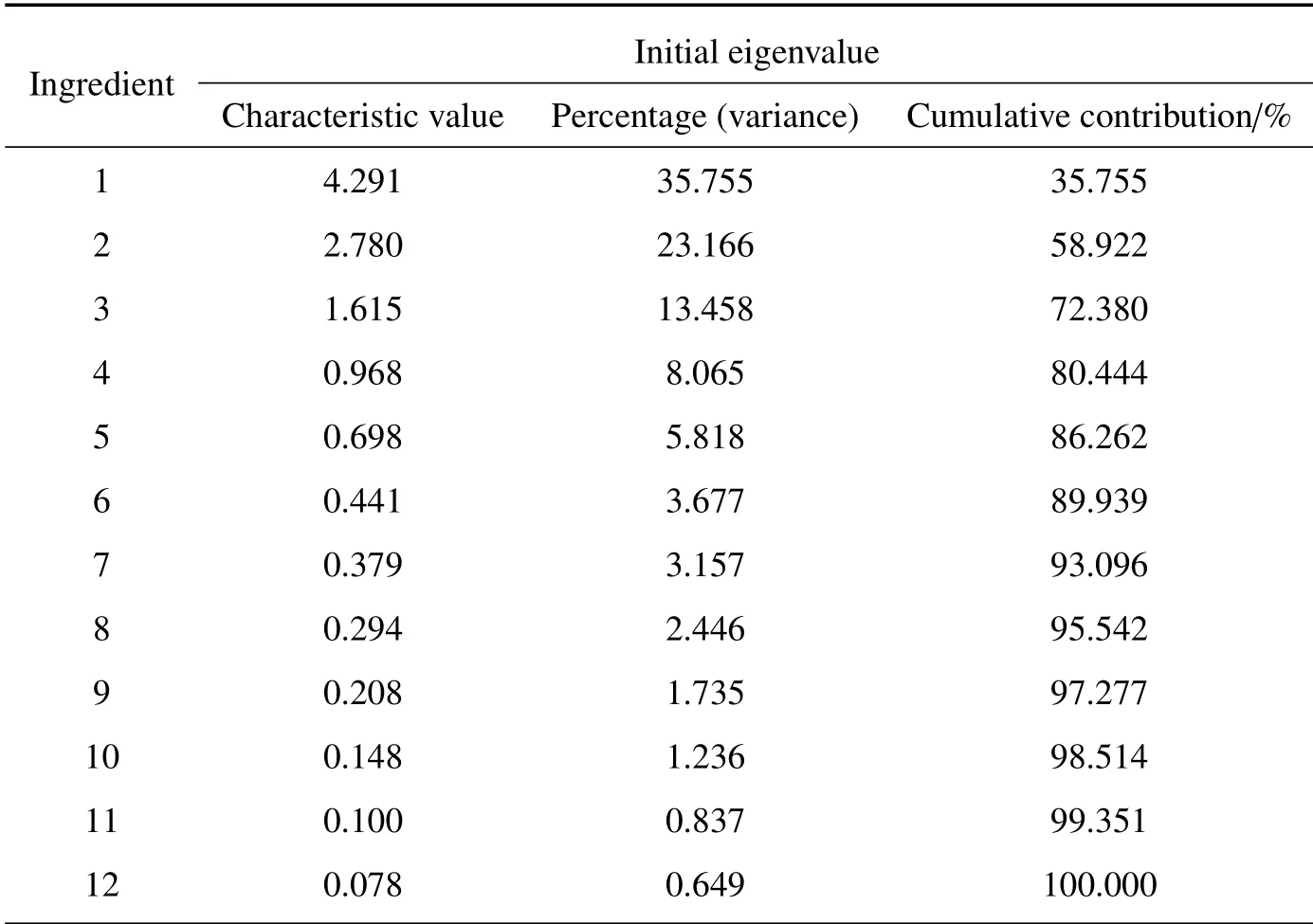
表2 总贡献率及初始特征值Table 2 Total contribution rate and initial eigenvalue
参数相关矩阵如表3所示。其中第一主成分中极大风速、CO、NO2、PM10、PM2.5、SO2的数值分别为0.587、0.893、0.856、0.682、0.830、0.744;第二主成分中最低气压、最高气温、最小相对湿度、O3的数值为0.827、0.823、0.660、0.732;第三主成分中日照时数的数值为0.662;第四主成分中最大风速的风向数值为0.672。因此第一主成分的参数包括极大风速、CO、NO2、PM10、PM2.5、SO2;第二主成分的参数包括最低气压、最高气温、最小相对湿度、O3;第三主成分的参数是日照时数;第四主成分的参数是最大风速的风向。其中与SO2同一主成分的是极大风速、PM2.5、PM10、CO、NO2,所以将第一主成分的参数作为PCA-RBF预测模型的输入量。
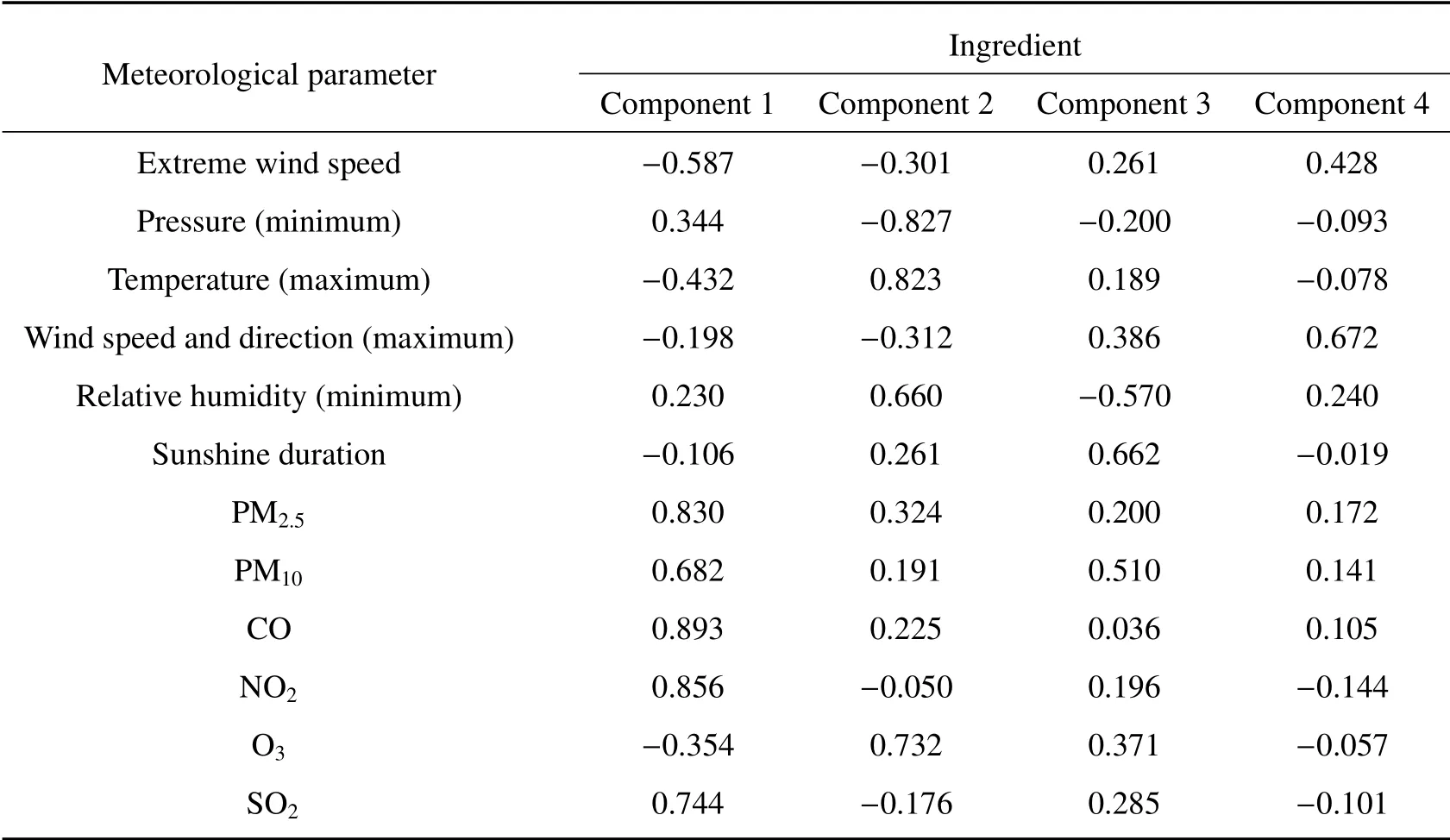
表3 气象参数相关矩阵Table 3 Correlation matrix of meteorological parameters
3 结果分析
利用北京大兴地区2019年9月1日至2020年10月31日参数作为神经网络样本,其中2019年9月1日至2020年9月31日共一年的气象数据作为训练样本,2020年10月1日至2020年10月31日共31天的气象数据作为测试样本。预测过程是先利用训练样本对10月1日的SO2浓度进行预测,将预测的结果作为第二天的输入量,以此类推,完成SO2浓度的滚动预测。
选用期望值与预测值的误差Ferror和相关系数R2两个指标对神经网络预测结果进行判断。两个指标的数学表达式分别为
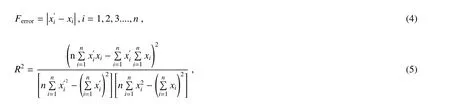
3.1 误差对比
由于预测模型是对未知参数进行估算,期望值与预测值的误差越小,表明预测值越接近期望值。通过RBF神经网络和PCA-RBF神经网络的期望值与预测值误差曲线(图2)可以看出,构建的RBF神经网络的期望值与预测值误差范围为0~0.2 μg·m-3,而PCA-RBF网络模型的误差变化幅度小,期望值与预测值误差范围为0~0.03 μg·m-3。因此,相对于RBF预测模型,PCA-RBF预测模型的期望值与预测值误差更小。
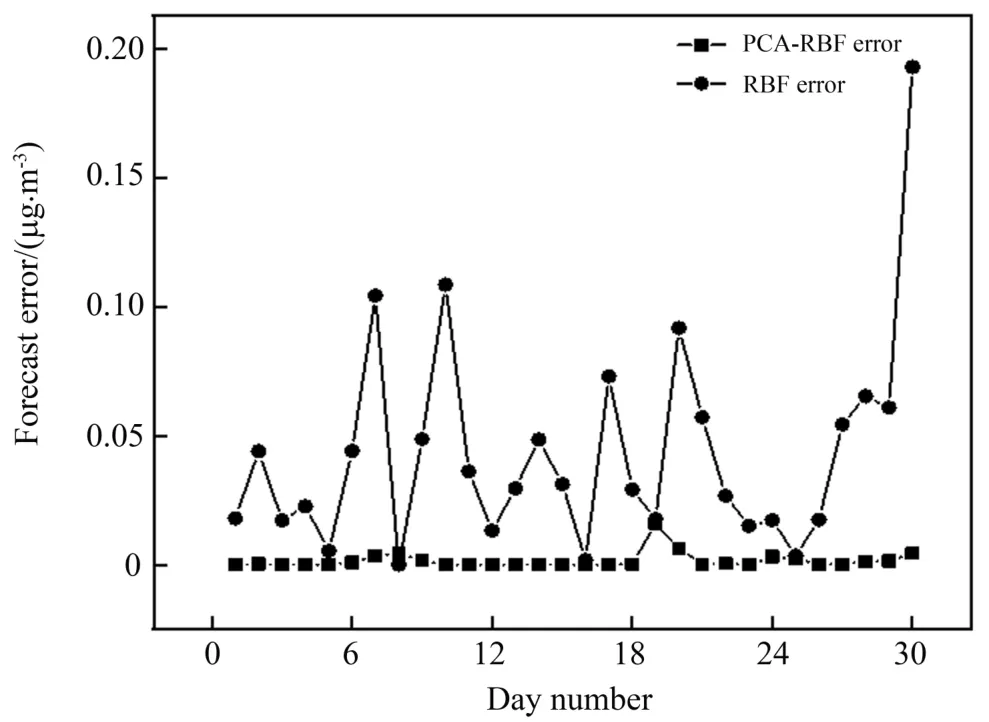
图2 神经网络预测误差对比Fig.2 Neural network prediction error comparison
3.2 相关系数对比
图3 (a)和(b)分别显示了两个预测模型PCA-RBF和RBF的期望值曲线和预测值曲线的对比结果。通过比对期望值和预测值的相关系数R2的大小判断预测效果[17]。RBF和PCA-RBF两个模型的期望值和预测值的相关系数R2分别为0.9758和0.9989。对比表明PCA-RBF网络模型中期望值与预测值相关系数大,期望值和预测值更为接近。
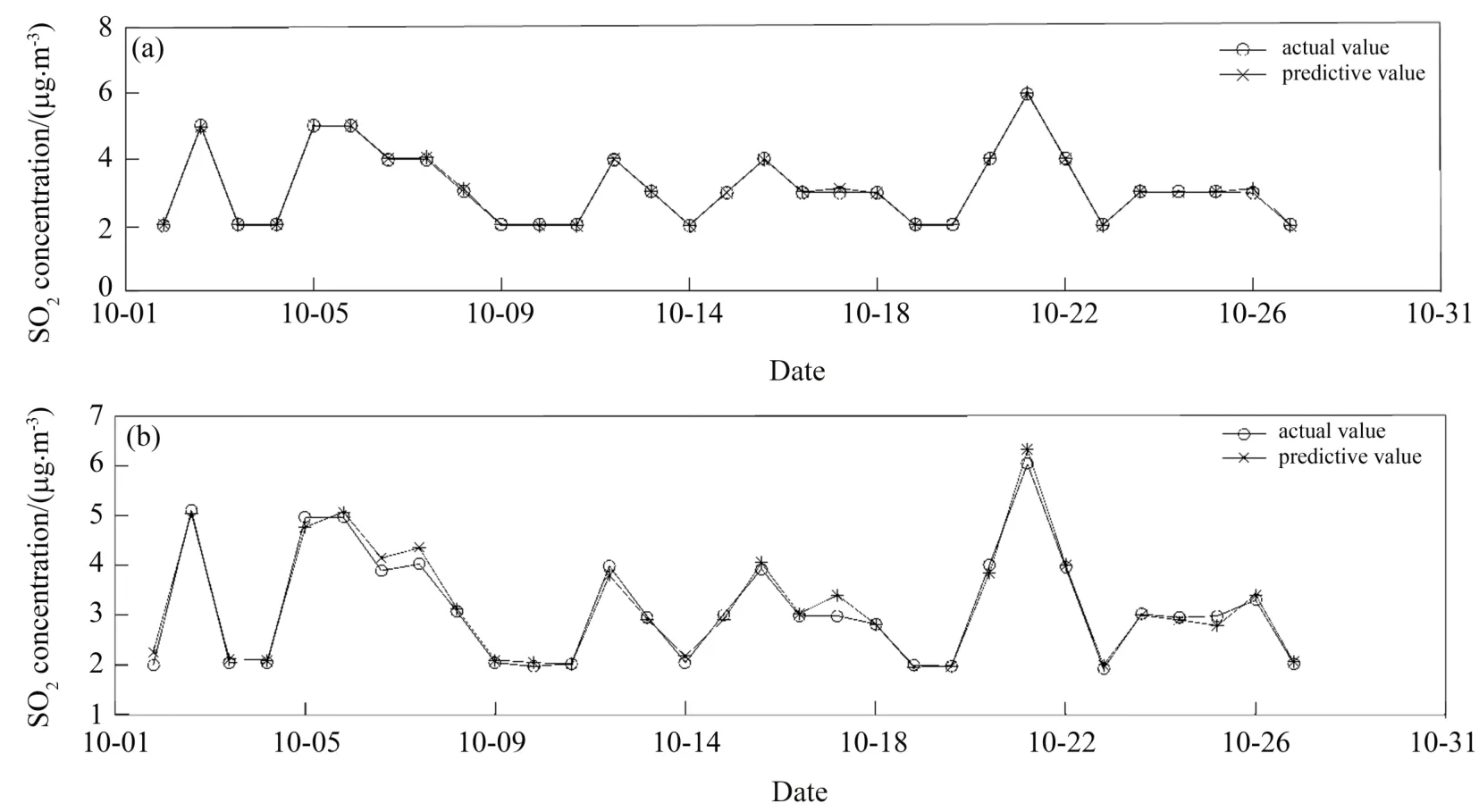
图3 PCA-RBF和RBF网络模型的预测值和期望值结果图。(a)PCA-RBF;(b)RBFFig.3 Comparison of predicted and expected values of PCA-RBF and RBF network models.(a)PCA-RBF;(b)RBF
4 结论
以北京大兴地区2019年9月1日至2020年10月31日的气象数据和空气质量参数作为基础,利用逐步回归法筛选出与SO2呈相关性的气象因子作为输入样本。结果显示:最高气压、NO2、CO、PM10、PM2.5、O3、气温最值、极大风速、最小相对湿度与SO2在0.01显著性水平上相关;最大风速的风向与SO2在0.05显著性水平上相关。构建了PCA-RBF预测模型,与RBF预测模型相比,PCA-RBF预测模型去除了无关参数的影响、减少了网络结构的输入变量、降低了算法计算成本。对比两个预测模型的误差和相关系数,结果显示PCA-RBF模型期望值和预测值的误差和相关系数分别为0.03 μg·m-3和0.9989,表明PCA-RBF神经网络能精确地预测SO2浓度变化趋势,可为进一步解决空气污染问题提供技术支持。
