蛋白质分子机器结构的特性分析及去折叠研究

张莉莉，蒋益锋，谢良旭，孔 韧，常 珊

（江苏理工学院电气信息工程学院生物信息与医药工程研究所，常州 213001）

引 言

在生物体内，由蛋白质组成的各种类型的分子机器驱动着各种各样的生命活动所必需的化学反应［1］。深入理解和分析蛋白质的结构特征，可以阐明蛋白质功能，解释蛋白质错误折叠引起的相关疾病起源，以及对于药物设计工作具有重要意义［2］。蛋白质GB1参与许多生理信号的检测，包括激素、神经递质和各种感觉刺激（光、气味等物质）［3］。此外，它还与疾病（例如朊病毒和阿尔茨海默病）相关的错误折叠状态的存在以及β聚集（淀粉样疾病）的研究相关［4］，因此关于GB1蛋白的研究具有重要意义。理解蛋白质GB1结构的折叠机制和稳定性是治疗人类疾病的重要基础，也有助于蛋白质的开发设计。近年来，关于蛋白质结构折叠的计算机模拟研究方法主要有两种，即分子动力学模拟和弹性网络模型。分子动力学模拟方法是一种细粒度方法，可以观察到蛋白质的折叠路径、过渡态等，但是该方法计算复杂、耗时较长，就目前计算机的模拟水平，仅仅只对一些小蛋白质分子的折叠结构模拟效果较好［5］。而弹性网络模型关键是给出适合简化模型的势函数，计算简单、耗时短，可模拟时间跨度大的去折叠过程，相对分子动力学模拟方法而言效率较高［6-7］，能够很好地再现蛋白质的低频运动（长时间动力学），提供关于它们的平衡动力学、天然结构拓扑对它们稳定性的影响、蛋白质波动的定位特性或蛋白质结构域的定义的信息［8］。弹性网络模型（Elastic network model，ENM）在蛋白质结构-功能关系研究中得到了广泛应用。先前有研究通过应用ENM来评估生物分子整体编码、蛋白质功能性运动分析和关键位点识别等［9］，此外，还有研究结果表明，应用ENM有助于更好地理解转运体系发挥生物学功能的分子机制。经典的弹性网络模型能够提供蛋白质在平衡态（通常为原生态）附近的动态特性，因此它们被广泛应用于许多蛋白质的系统比较。然而，蛋白质折叠通常远离平衡态，所以一般的ENM不适合蛋白质折叠的研究。蛋白质结构预测一直是生命科学里的一个重要问题，研究蛋白质序列和结构间关系的蛋白质折叠问题是生物物理领域最重要的基础问题之一。在2020年举办的第14届蛋白质结构预测竞赛CASP14（Critical assessment of protein structure prediction）中，Google DeepMind团队使用AlphaFold2预测了多个物种中共30余万个无实验结构的蛋白质的结构模型，并联手EBI建立了结构预测数据库AFDB［10］。这一系列成果的出现吸引了科学界的大量关注。AlphaFold2等结构预测方法目前仅能预测特定氨基酸序列的静态构象。蛋白质在行使生物学功能时往往需要发生构象变化。比如酶从失活状态转变为活性状态、膜转运蛋白需要通过构象变化交替接触膜两侧的溶液、蛋白和配体结合时发生构象变化等等。高斯网络模型（Gaussian network model，GNM）是经典ENM方法的发展，是一种基于拓扑的、不依赖序列特异性的粗粒度模型。高斯网络模型可以从晶体结构提供蛋白质构象转变的信息，不需要分子动力学模拟的高计算成本，是一种基于正态模式计算的迭代方法，被提出来用于研究蛋白质折叠/去折叠过程。多年来，GB1在蛋白质折叠的计算和实验研究中被广泛用作模型系统［11］。本文主要就是通过利用弹性网络模型，模拟GB1蛋白结构的展开过程，再现GB1的快运动与慢运动模式，同时研究它的拓扑结构对自身稳定性的影响。

1 蛋白质结构

本研究选择分析的蛋白质GB1（PDB代码：6CHE）如图1所示［12］。GB1是一种小球状蛋白，由β折叠和α螺旋组成，共有56个残基。8个残基与W43形成天然接触：其中4个残基（F52、T53、V54和T55）位于相邻的β折叠中，并与W43的骨架形成天然接触，而其他4个残基（L5、F30、K31和M34）与W43的侧链相互 作 用。在GB1中，残 基2-19形 成N端β折 叠，残 基23-36形成α螺旋，残基42-55形成C端β折叠［13］。

2 本文方法

2.1 高斯网络模型

在高斯网络模型中，每个蛋白质的三维结构可以简化为一个弹性网络，其中每个氨基酸（残基）被看作为该网络中的顶点，如果两个顶点间距离小于截止距离，则用一根弹簧将其连接，所有弹簧的弹性系数都相同［14］。基于该网络模型，网络的总能量可以写成

式中：V为所有接触残基的总能量；γ为弹性系数；{ΔR}为残基涨落的N维列向量；Γ为N阶对称矩阵，在对称矩阵中的元素可写为

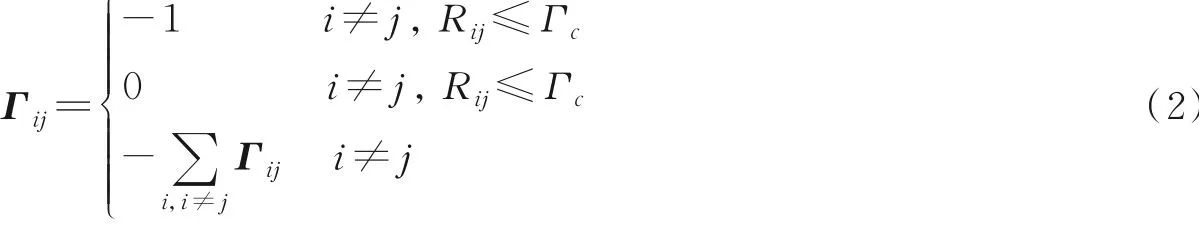
式中：Rij为蛋白质中第i个和第j个残基之间的距离；Γc是截止距离（本研究中采用的截止距离为7.4Å）。

N阶对称矩阵Γ的逆矩阵可表示为

式中：U为正交矩阵，其列向量Ui（1≤i≤N）是Γ的特征向量；Λ为对角矩阵，其对角线上的元素是Γ的特征值。

蛋白质中两个残基均方涨落的互相关性计算可表示为

式中：i和j分别表示蛋白质中第i个和第j个残基；kB为玻尔兹曼常数；T为绝对温度。当i=j时，第i个残基的均方涨落计算式可表示为

根据Debye-Waller理论，第i个残基的B因子计算式可表示为

在高斯网络模型中，归一化的互相关性系数可写成［15］

高斯网络模型是建立在多聚体网络的波动动力学基础之上的，弹性网络模型可以是原子层次上的粗粒化模型，也可以是残基层次上的粗粒化模型。高斯网络模型模拟方法可以把蛋白质的功能性运动分解成为各个不同种运动模式的叠加，在不同种运动模式中，慢运动模式为对应着与蛋白质功能相关的大幅度集合运动［16］。通过与实验数据的对比可以发现这种方法所得到的数据结果是可靠且有效的。

2.2 去折叠原理

为了研究蛋白质的去折叠过程，本文提出了一种基于高斯网络模型的迭代方法。所有残基对之间距离的均方涨落都是基于高斯网络模型计算的，第i个残基和第j个残基之间距离的均方涨落可表示为［17］

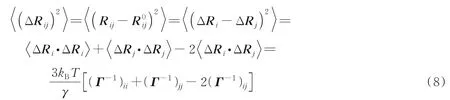
式中：Rij和分别为残基i和残基j之间的瞬时和平衡分离向量。

蛋白质结构去折叠过程的模拟方案如下：

（1）基于式（8）和蛋白质的天然拓扑结构计算出结构中所有残基对之间距离的均方涨落值；

（2）断开距离均方涨落值最大的残基对之间的天然接触，得到对应新Γ矩阵的结构拓扑；

（3）基于新的Γ矩阵，利用式（8）重新计算所有残基对之间距离的均方涨落值；

（4）重复上述两个步骤，直到蛋白质中所有的非共价接触被断开；

（5）综合由以上步骤得到的所有结构拓扑信息，以获取蛋白质的去折叠过程。

3 结果与讨论

3.1 实验与模拟所得的B因子分析

为了评价高斯网络模型方法在本研究中应用的可行性，计算了B因子，并与X射线（X-RAY）实验数据对比。根据GNM模拟所得的数据与X-RAY实验结果对比结果如图2所示，其中，红色曲线对应基于GNM模拟所得的数据，绿色曲线对应X-RAY实验数据。可以看出，两条曲线的峰值和谷值出现的位置几乎相同，模拟所得的数据与实验数据之间的相关系数为0.70。综合以往的文献研究得到，一般模拟数据与实验数据之间的相关系数取值为0.53～0.89［6，14-15，18］，本 次 实 验结 果 所得 值 为0.70，在 此 范围内，可见该方法是适用的，表明该模型适用于研究GB1蛋白的固有动力学。

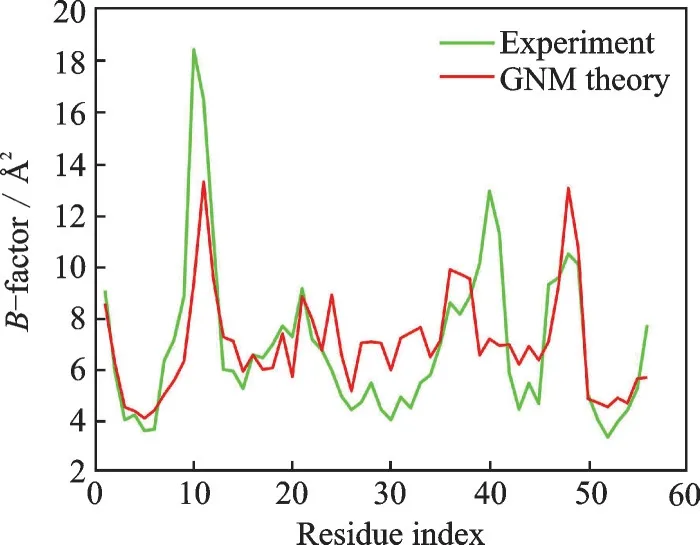
图2 实验与模拟所得的B因子对比Fig.2 Comparison of B factor between experiment and simulation

3.2 蛋白质的快运动与慢运动模式分析

运动的快模式对应于局部结构中的几何不规则性。以前的研究发现，高频波动残基被认为是动力学关键残基，对三级折叠的稳定性至关重要［19］。图3显示了GB1蛋白的快运动模式。图3中，横坐标表示残基序号，纵坐标表示残基自身距离的均方涨落值，基于式（5）求得，单位为平方埃（Å2）。从图3可以看出，残基Lys4、Ala26、Thr51和Val54（图中已标注）是曲线中的峰值。本文结果与以前的研究［20］一致，表明这些残基在蛋白质的稳定性中起着关键作用。

图3 GB1快运动模式结果Fig.3 The fastest mode shapes of GB1

在蛋白质的研究过程中，慢运动模式代表着蛋白质结构中编码的长程集体运动，同时相关研究认为那些慢运动模式就相当于大幅度的集体运动，而大幅度集体运动往往与蛋白质运动相关［21］。图4显示了基于高斯网络模型计算的GB1蛋白的最慢模式。从图4可以看出，大多数残基波动值较高，这意味着这些结构相对而言不是很稳定。同时，还可以从图中看出，残基Gln2、Tyr3和Thr18的波动值保持较低。

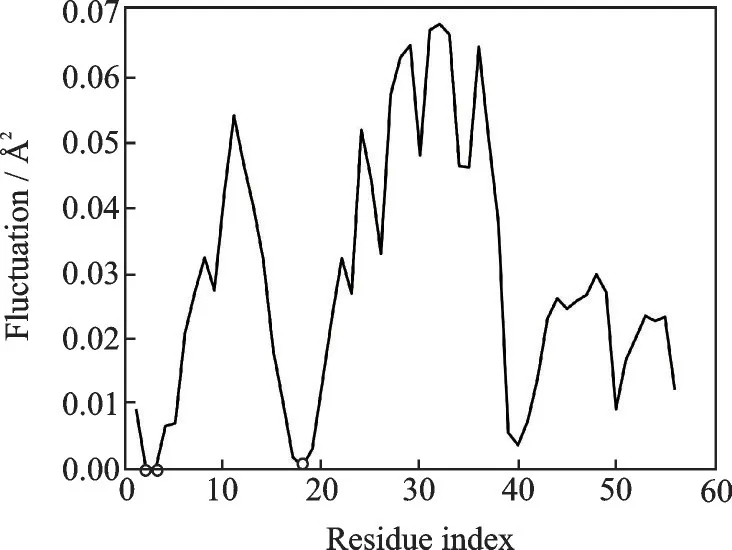
图4 GB1慢运动模式结果图Fig.4 The slowest mode shapes of GB1

3.3 蛋白质去折叠过程分析

为了详细说明展开模拟过程中自然接触的损失，构建了不同快照中构象的接触图，结果如图5所示。图5（a）显示了GB1蛋白天然结构的接触图，即当两个残基之间的距离小于7.4Å时，两个残基被定义为相互接触。如果两个残基直接有接触，则用*表示，图5（b～f）分别展示了GB1蛋白的非共价接触损失数（Loss number of noncovalent contact，LNNC）分别为20、50、100、130和170的结果。图5（a）天然状态下的接触呈现结果与之前的相关研究一致［22］。结果表明，GB1蛋白的展开有一个优先的过程，它显示了一系列事件。

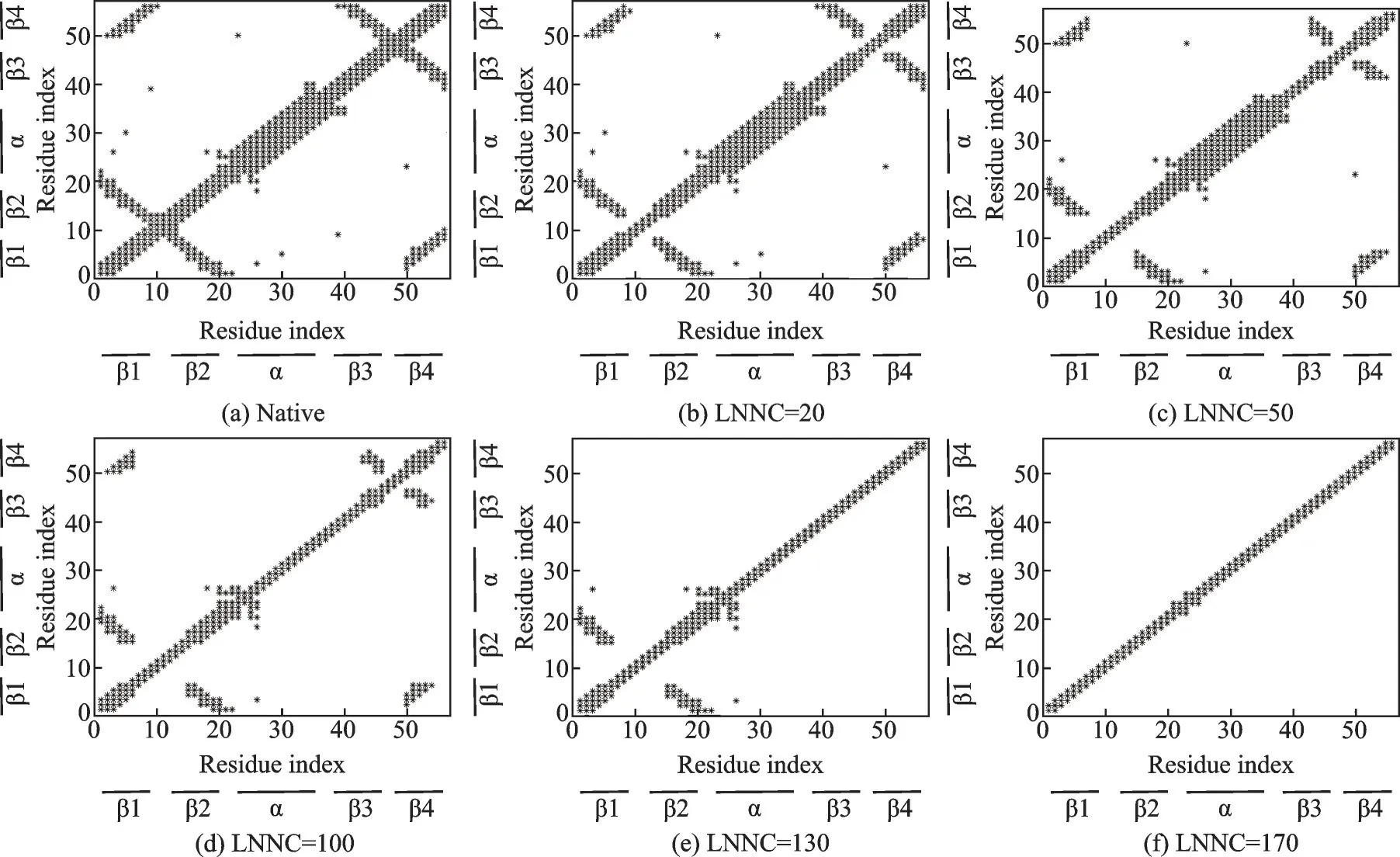
图5 GB1天然结构以及非共价接触损失数分别为20、50、100、130和170的接触图Fig.5 Contact maps of native conformation and conformations with LNNC of 20,50,100,130,170 for GB1

由图5（a）可以看出，在GB1的天然结构中，碳末端折叠比氮末端折叠有更多更强的接触（图1），这可能导致碳末端区域更快的折叠。从图5（b，c）的实验结果可以看出，随着残基对之间非共价接触损失个数的增加，GB1蛋白一开始主要是从β2折叠部分的残基对之间的接触先断开，此外，从图5（c）也可以看出β4在非共价接触损失数为50左右的时候开始断开了。继而如图5（d，e），α螺旋部分的残基对之间的接触再逐渐断开，直至如图5（f），最终几乎所有接触断开，即GB1蛋白完全展开。该过程显示了GB1蛋白的展开是从大量的α螺旋和β2折叠结构元素的接触损失开始，同时先保持了大部分其他β结构的完整。本模拟结果与之前的实验研究结果一致［13］。

此外，折叠协同性被认为是蛋白质折叠动力学的一个重要行为［23］。在本研究模型中，展开路径是连续的，很难直接观察展开过程中的协同性。事实上，这些高度合作的行为发生在这个迭代展开模型的近邻步骤中。结果表明，解折叠路径主要由其自身的拓扑结构决定，迭代解折叠方法可以合理地描述GB1的去折叠过程。

3.4 蛋白质去折叠过程中的互相关分析

此外，本文还研究了在GB1蛋白去折叠过程中残基波动之间的相关性的变化。残基波动之间的互相关用式（7）计算。互相关值的取值范围为-1到1。其中，正值表示残基间运动方向相同，负值则表示它们之间运动方向相反。绝对互相关值越高，两个残基越相关（或反相关）。另外，互相关值0意味着残基的运动完全不相关［14］。图6显示了GB1蛋白的互相关图。

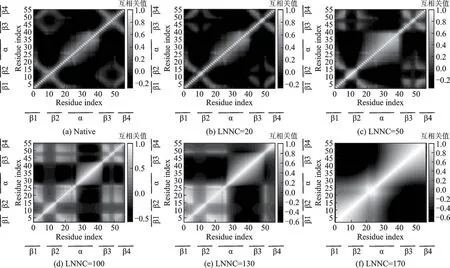
图6 GB1天然结构以及展开过程中非共价接触损失数分别为20、50、100、130和170时的残基互相关图Fig.6 Cross-correlation maps calculated using all modes for native conformation and conformations with LNNC of 20,50,100,130,170 during the unfolding process of GB1

如图6（a）所示，沿着图的对角线，有一些正相关的光块，对应α螺旋和β折叠的二级结构。随着残基对之间非共价损失个数的增加，即随着GB1蛋白的逐渐展开，如图6（b，c），当α螺旋和β折叠中的天然触点开始丢失时，α螺旋和β折叠之间负相关，β折叠之间的正相关性提高；随着天然触点丢失个数的增加，如图6（d，e），α螺旋和β折叠仅部分保留，最后，如图6（f），蛋白质的结构似乎被分成两个方向相反的方向波动。该图反映的是去折叠的最后状态，即蛋白质结构展开回到了最初未折叠的多肽链结构。根据先前的研究发现［14］，当去折叠模拟到最后的阶段时，蛋白质的结构也似乎被分为两部分，上下波动方向相反，与本次实验结果一致。

4 结束语

本研究基于GB1的拓扑结构，采用高斯网络模型模拟了GB1的快运动与慢运动模式，并对其做了相应的结果分析；同时，对其拓扑结构做了展开过程的路径研究；此外，还研究了GB1蛋白在去折叠过程中残基波动之间相关性的变化。与相关实验和分子动力学模拟数据吻合良好，表明弹性网络模型的计算效率高，能够准确模拟蛋白质的动态和结构特性，能够很好地再现蛋白质的运动特性，提供关于它们的平衡动力学、天然结构拓扑对其稳定性的影响、蛋白质波动的定位特性或蛋白质结构域的信息，适用于对蛋白质的研究。