超宽带系统中基于DFT的TOA/DOA联合估计方法

沈 超，郭雅娟，俞家融，杨静泊，徐江涛

（1.国网江苏省电力有限公司无锡供电分公司，无锡 214000；2.国网江苏省电力有限公司电力科学研究院，南京 211103）

引 言

脉冲超宽带技术以传输极短持续时间脉冲为特征，即以纳秒级甚至亚纳秒级脉冲为载体传输信息的无线通信技术，能够实现非常精确的测距和定位应用，因而广泛应用于雷达、物流、搜救和交通导航等领域［1-2］。在无线定位系统中，定位参数主要包括到达时间（Time-of-arrival，TOA）［3］、波达方向（Direction-of-arrival，DOA）［4］、到达时间差（Time-difference-of-arrival，TDOA）［5］和接收信号强度（Received signal strength，RSS）［6］。其中，TOA参数估计由于超宽带（Ultrawideband，UWB）信号的高时间分辨率，成为UWB系统中位置估计的一个很好的方法。

事实上，大多数UWB系统的定位技术都是基于TOA参数估计方法，因为它们能够利用大信号带宽。由于TOA参数只能获得距离信息，仅利用TOA参数进行定位的系统需要的观测节点数较多，增大了系统的成本。基于DOA估计的定位技术有助于减少位置估计所需的节点数。综合利用TOA参数提供的距离信息和DOA参数提供的方向信息，只需单个观测节点即可实现目标源的位置估计，能有效降低系统的复杂度。同时，若TOA参数和DOA参数的估计精度较高，还可以使得系统的定位精度更高。

目前，超宽带系统中TOA参数和DOA参数的联合估计方法已经得到了较为广泛的研究［7-21］。按照信号处理的域的不同进行分类，可将现有的方法分成时域估计算法和频域估计算法两种。传统基于时域信号处理的参数估计方法主要包括采用高采样速率匹配滤波技术的相干检测方法以及采用较低采样率的能量检测方法。文献［7］提出了一种阈值检测匹配滤波器输出的三步TOA估计算法。该算法首先通过峰值检测匹配滤波的输出，得到直达单径（Direct path，DP）的TOA搜索区域，然后在该搜索区域进行阈值检测，得到直达路径的TOA粗估计结果，最后精确搜索粗估计值附近的TOA参数，得到精估计值。由于相干方法依赖于极高的采样率，因而对采样设备的要求很高，不易于硬件实现。文献［8］提出了一种易于实际应用的基于双脉冲信号自相关的TOA估计方法，该方法从搜索区域中的不同起点开始执行长度等于脉冲持续时间的自相关步骤，通过确定自相关结果第一次显著下降的位置，即遇到多径分量的位置，结合门限检测实现TOA参数估计。该方法无需高速率采样，因而实现起来比较简单。但是由于在低信噪比或非视距环境中DP成分的能量衰落严重，性能极易受到干扰，并且该方法中最优门限的选择依赖于脉冲自动增益控制和信噪比估计，不可避免地会增加系统的复杂度。

由于传统基于时域信号处理的参数估计方法分辨率低、对接收设备要求高，学者们又对超分辨率TOA和DOA估计技术进行了研究，提出了基于多信号分类算法（Multiple signal classification，MUSIC）［9-10］、矩阵束［11-12］、传播算子（Propagator method，PM）［13-14］和总体最小二乘基于旋转不变技术的信号参数估计（Estimating signal parameter via rotational invariance techniques，ESPRIT）［15-21］的一系列联合估计算法。文献［10］利用了具有超分辨力的二维MUSIC算法，通过扩展频域自相关矩阵得到扩展的噪声子空间，然后利用信号子空间和噪声子空间的正交性，构造二维谱函数实现TOA估计。该方法在提高分辨率的同时也增加了系统实现的复杂性，在处理短时信号时由于仅有单快拍数据导致相关矩阵的秩亏，性能大大下降。针对这个问题，文献［12］提出的矩阵束算法不需要计算信号的协方差矩阵，可以直接对接收到的信号数据进行处理，具有分辨率高、计算速度快的优点，只需要单快拍就可以估计出位置参数；缺点是对信噪比要求高，在低信噪比下性能差。文献［14］将PM算法应用到TOA估计中，通过空间平滑方法解决了超宽带（Ultrawideband，UWB）环境下信号振幅相关导致的相关矩阵秩不足的问题。该方法在提升算法估计精度的同时无需MUSIC方法中的特征值分解步骤，因此与MUSIC方法相比需要较少的计算量。但是该方法中的广义逆求解和额外的空间平滑仍具有较高的复杂性，不利于硬件实现。

为了进一步提升参数估计的精度，同时避免额外的计算复杂度，本文提出了一种基于离散傅里叶变换的TOA和DOA联合估计方法。该算法首先对接收信号频域内建模，得到相应协方差矩阵。充分利用导向矩阵的范德蒙德特性，通过对协方差矩阵进行离散傅里叶变换（Discrete Fourier transform，DFT）处理，得到信号到达两根天线的TOA粗估计结果。然后通过设计补偿矩阵对时延矢量进行相位补偿，搜索得到TOA粗估计结果的补偿值，从而获得TOA精估计结果。最后进行参数配对并根据信号到达两根天线的到达时间差得到DOA估计结果。该方法无需特征值分解以及广义逆求解步骤，在获得较好的参数估计性能的同时，复杂度也比较低，易于工程实现。大量仿真实验结果证明，本文所提方法能够很好地实现TOA和DOA的联合估计，相比于文献［12］中的矩阵束算法和文献［14］中的传统PM算法，本文提出的方法性能有很大幅度的提高。相比于基于阵列天线的参数估计系统，本文的方法仅需两根天线即可实现TOA和DOA的联合估计，降低了成本。

1 脉冲无线电超宽带系统中的数据模型

考虑一个基带信号为直接序列二进制相移键控（Direct sequence binary phase shift keying，DS-BPSK）调制的脉冲无线电超宽带（Impulse radio ultra wideband，IR-UWB）系统，利用Nc个重复的二进制数据符号的脉冲完成发射信号的传输。设二进制数据符号的周期为Ts，脉冲重复周期为Tc，则超宽带系统的发射信号可表示为［11，21］

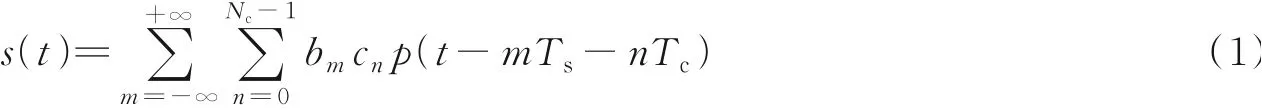
式中：bm为被调制的二进制数据符号序列；cn为用于多址通信的伪随机序列；bm、cn∈{-1，+1}；p(t)为高斯脉冲的二阶导数，形式如下

式中Γ为脉冲形成因子，与脉冲宽度相关。

假设超宽带信道传输的信号簇数为K，每一簇中存在的多径数为L。不失一般性地，假设各多径分量的传输时延与信号簇数无关，则第k簇传输信号的多径衰落传播信道可以表示成［18-20］

式中τl和分别为信道传输过程中第k簇第l径的传输时延和衰落幅度为信道衰减系数，服从瑞利分布为随机变量，服从均匀分布。则UWB系统的接收信号可以表示为发射信号和信道冲激响应的卷积，即

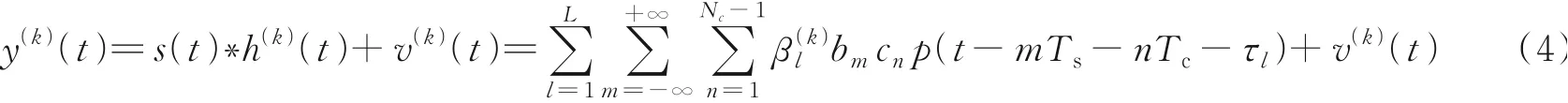
式中v(k)(t)为第k簇信号接收时产生的加性高斯白噪声。将式（4）转换到频域并进行N(N＞L)点等间隔采样，得到离散频域接收信号的形式为

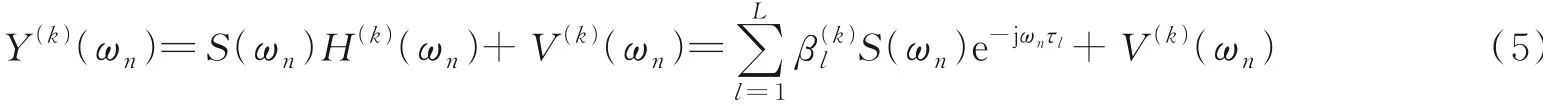
式中ωn=nΔω，n=0，1，…，N-1，Δω=2π/N为频域采样间隔。将采样的离散数据排列成N×1维列向量[Y(k)(ω0)，…，Y(k)(ωN-1)]T，记为yk，则可以得到第k簇频域接收信号的向量表示［11，21］

2 IR-UWB系统中TOA和DOA联合估计

2.1 IR-UWB系统的信号接收模型

考虑如图1所示的阵列接收模型，接收系统由两根相距距离为d的天线组成。假设信号源位置为阵列天线的远场，则入射到天线阵列的信号可以被视为一束平行波，天线1和天线2的接收信号仅在时延上有差异。

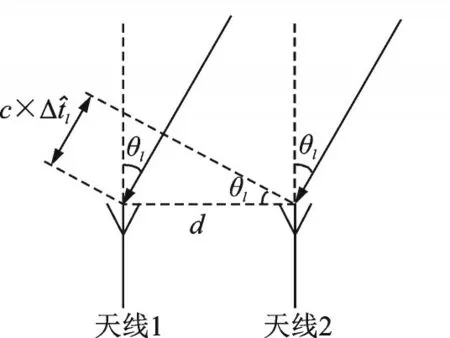
图1 阵列天线示意图Fig.1 Schematic diagram of array antennas

根据式（6）表示的第k簇频域接收信号的向量形式，采集K簇接收信号，则可得天线1和天线2的频域接收信号的矩阵形式Y1和Y2，分别表示为［21］

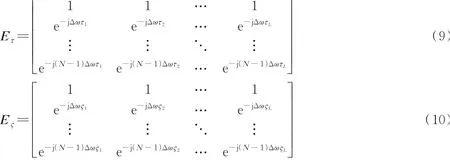
式中：B=[β1，…，βk，…，βK]为由信道的复数衰落幅度组成的L×K维矩阵；V1和V2分别为由天线1的频域噪声向量和天线2的频域噪声向量组成的N×K维矩阵；Eτ和Eς分别为天线1和天线2的时延矩阵，表示为

假设第l个多径的入射角为θl，则天线1的接收信号相对于天线2的接收信号的到达时间差可以表示为式中c为真空中光传播的速度。根据式（7）可得第l个多径的DOA估计表达式为

2.2 基于DFT的TOA粗估计

将式（7）和式（8）两边同时除以矩阵S，得到新的矩阵分别记为则新的接收信号矩阵形式为

式中：W1=S-1V1；W2=S-1V2。考虑到S是对角矩阵，因此只需计算S的N个对角元素的倒数组成的对角矩阵即可得到S-1。在不考虑噪声的情况下，式（13，14）构造的接收信号的采样协方差矩阵可以计算为

式中RB=E[BBH]。考虑到DFT方法只能作用于单快拍数据，因此分别取协方差矩阵R̂1和R̂2的第1列，可得

定义N×N维归一化DFT矩阵

为了简便，记qτ=RB IL×1/K，qς=RB IL×1/K。对构造的单快拍接收信号r1和r2分别进行DFT处理，得到DFT后的数据形式为

式 中：xi为向 量x的 第i个 元 素分 别 为 单快 拍 接收 信 号 向量r1和r2经 过DFT处 理 后的 结 果和分别为由时延矩阵Eτ和Eς的第l列组成的列向量。

将式（19）中矩阵F的表达式代入式（20，21），可得

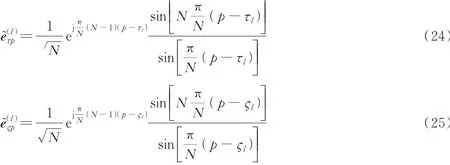
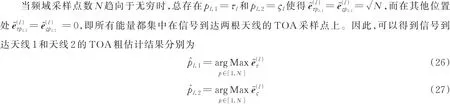
将式（26，27）得到的TOA估计结果代入式（12），可以得到DOA估计为

根据商务英语专业跨境电商方向人才培养目标和对行业企业的调研，在全面分析跨境电商岗位所需知识结构和岗位技能的基础上，我们提出基于职业素养的岗位基本能力、岗位核心能力和拓展能力构建跨境电商方向的课程体系。

2.3 基于DFT的TOA精估计

在实际中，由于硬件设备的限制，信号到达天线阵列的时延可能不会落在采样点上，同时由于频域采样点数N是有限的以及噪声的影响，式（24，25）的离散序列无法呈现理想稀疏形式，总能量会分散在TOA及其附近的采样点上。考虑到频域采样点数N≫1，仍然可以通过式（24，25）的峰值位置来估计TOA参数，但是TOA参数估计的精度总是受限于频域采样间隔，以第1根天线为例说明，即通过式（26）得到的TOA估计结果可能为，该结果与真实的TOA参数之间总是存在一个微小误差。因此本文进一步对TOA粗估计结果进行补偿，通过搜索得到微小误差的估计值，从而得到精确的TOA估计结果。

定义相位补偿因子的间隔为ξ，搜索次数为J+1，相位补偿因子μ∈[-Jξ/2，Jξ/2]，则N×N维相位补偿矩阵可以表示为

对相位补偿后的数据再次进行DFT处理，可以得到与式（22，23）类似的形式如下

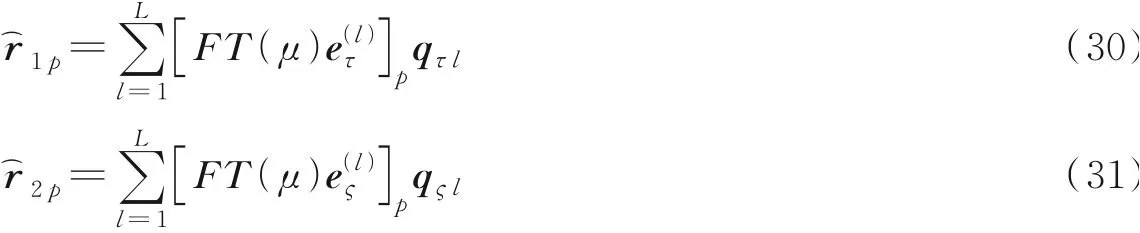
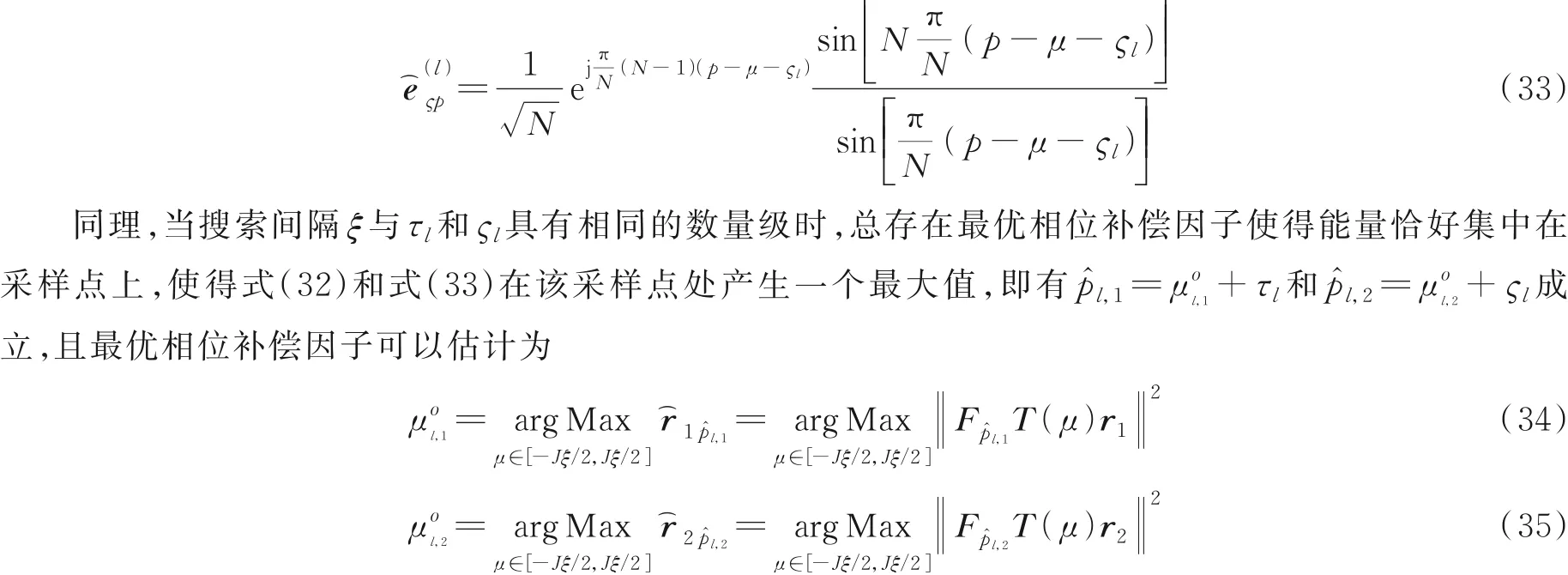
则最终的TOA精估计结果可以表示为

2.4 配对

2.5 基于DFT的TOA和DOA联合估计步骤

至此，可以将IR-UWB系统中基于DFT的TOA和DOA联合估计方法的主要过程总结为如下步骤：

（1）将两根天线的接收信号转换为频域形式，并通过两边同时除以式（6）中的对角矩阵S构造新的接收信号矩阵，根据式（15，16）得到的协方差矩阵估计值

（3）利用DFT后的离散序列r͂1和r͂2的稀疏性质，根据式（26，27）得到信号到达两根天线的TOA粗估计结果

（4）根据式（29）构造相位补偿矩阵Τ(μ)，根据式（30，31）对相位补偿后的数据再次进行DFT处理，根据式（34，35）得到最优相位补偿因子的估计值，根据式（36，37）得到TOA精估计结果

（5）根据式（38）将两根天线的估计结果中对应于同一多径分量的TOA估计值进行配对，根据式（39）得到DOA估计结果。

2.6 算法的复杂度分析

本文所提算法的复杂度主要包括以下方面：构造N×K维频域接收信号矩阵，计算复杂度为O(N2+2KN2+N+2KN)；计算的协方差矩阵估计值，计算复杂度为O(2KN2)；对N×1维列向量r1和r2做DFT处理，计算复杂度为O(2N2)；对N×1维列向量r1和r2进行相位补偿，计算复杂度为O(2N2)；搜索得到最优相位补偿因子，计算复杂度为O((J+1)N)；两根天线的TOA估计值匹配，计算复杂度为O(L2(L3+2L2+2NL+N+1))。

综上所述，本文所提算法的总复杂度为O((5+4K)N2+(J+3+2K+2L3)N+L5+2L4+L2)。对于文献［12］中的矩阵束算法，总的计算复杂度为O((2K+1)N2+(2K+6KL2)N-2KL3)。对于文献［14］中的传统PM算法，总的计算复杂度为O((4K+2L+1)N2+(2K+2L2)N+2L3+4(NL)3+4N(N-L)2+2m(N+1)(N-L))。图2为本文所提算法与矩阵束算法、传统PM算法在相同条件下的复杂度比较，参数设置为信号簇数K=500，多径数L=3，PM算法谱峰搜索次数m=2 000，所提算法精搜索次数J=401。本文所提算法的计算复杂度在频域采样点为512点以下时计算复杂度低于另外两种算法，在频域采样点高于512点时略高于传统PM算法，显著低于传统PM算法。

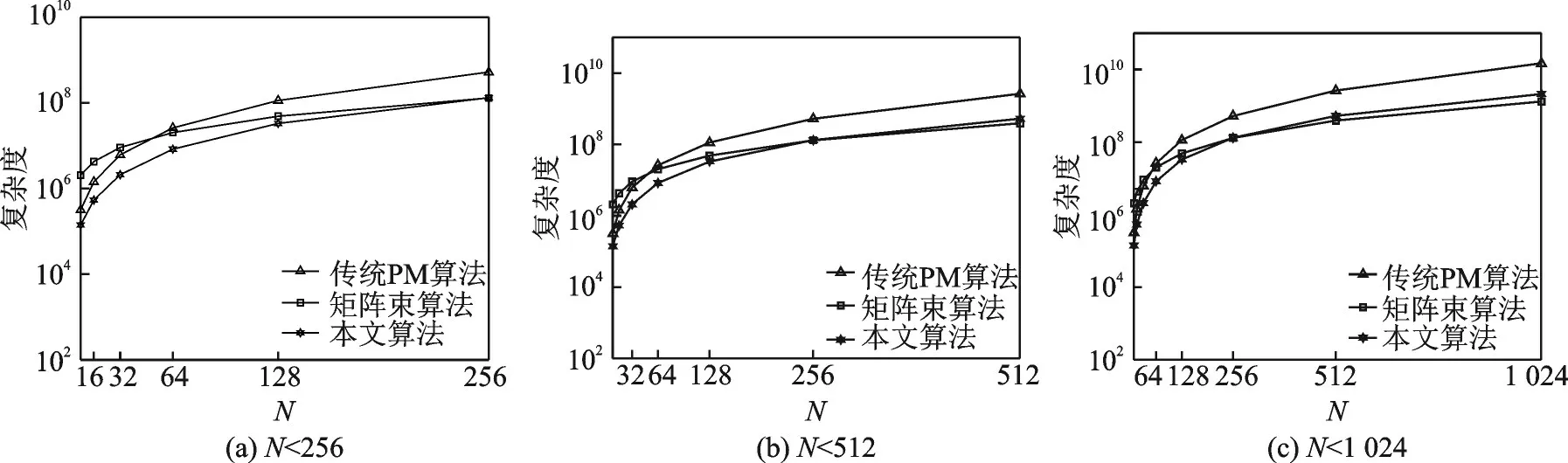
图2 各算法复杂度对比Fig.2 Comparison of the complexity of each algorithm

2.7 算法优点

本文提出的TOA和DOA联合估计算法具有以下优点：

（1）所提算法无需MUSIC类算法中所需的复杂特征值分解步骤。

（2）与矩阵束算法［12］相比，所提算法不需要复杂的广义逆求解，大大降低了系统的复杂性。

（3）在相同的仿真条件下，所提算法的TOA和DOA联合估计性能优于矩阵束算法［12］和PM算法［14］，且复杂度低，易于工程实现。

3 计算机仿真

为了验证本文所提算法的有效性，本节采用Monte Carlo仿真实验来评估算法的TOA和DOA联合估计性能。定义信噪比采用均方根误差（Root mean square error，RMSE）来衡量算法的参数估计性能，定义如下

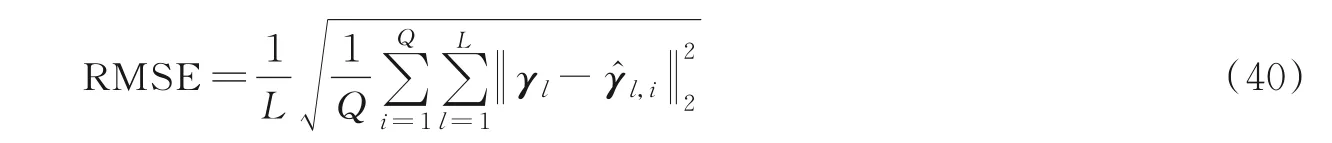
式中：Q为蒙特卡洛仿真实验的次数分别为第i次蒙特卡洛仿真实验中对应于第l个多径参数的真实值和估计值。

假设仿真中涉及的噪声均为加性高斯白噪声，发射信号参数设置为：脉冲形成因子τm=0.1 ns，脉冲重复周期Tc=2 ns，单个符号的脉冲重复次数Nc=5，频域采样点数N=64，信号簇数K=500，每一簇的多径数L=3。

仿真1假设L=3个多径入射到天线1的到达时间分别为0.2、0.3、0.4 ns，信号波达方向分别为10°、20°、30°，在信噪比为20 dB的情况下，用本算法进行50次Monte Carlo仿真，得到TOA和DOA联合估计散布图分别如图3和4所示。可以看出本文所提的算法具有良好的联合参数估计性能。

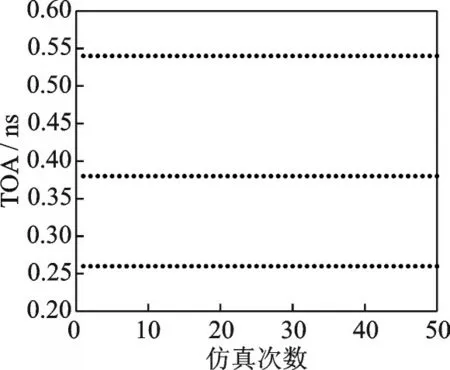
图3 SNR=20 dB时的TOA估计散布图Fig.3 Scattered plot of the estimated TOA at SNR=20 dB

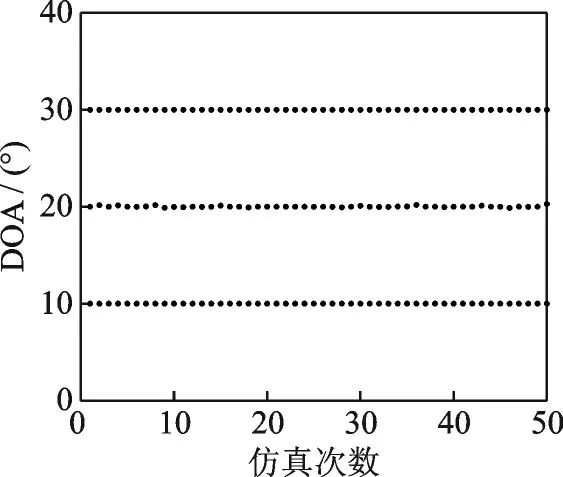
图4 SNR=20 dB时的DOA估计散布图Fig.4 Scattered plot of the estimated DOA at SNR=20 dB

仿真2图5为本文所提算法在不同多径数L下的TOA估计性能，多径入射到天线1的到达时间分别为0.2、0.3、0.4 ns，信号波达方向分别为10°、20°、30°。由图5可以看出，在信噪比相同的条件下，所提算法的TOA估计性能随着多径数L的减少而提升。图6为本文所提算法在不同频点下的TOA估计性能，多径入射到天线1的到达时间分别为0.2、0.3、0.4 ns，信号波达方向分别为10°、20°、30°。由图6可以看出，在信噪比相同的条件下，所提算法的TOA估计性能随着频点的增加而提升。

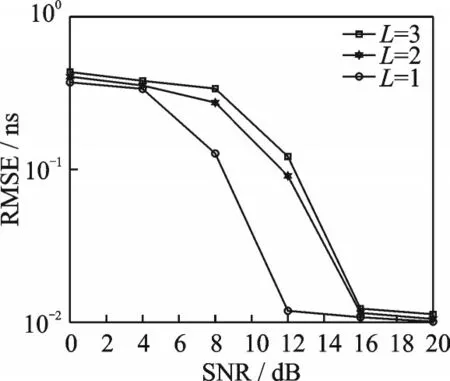
图5 本文算法在不同多径数下的TOA估计性能Fig.5 Estimated performance of the proposed algorithm for TOA at different multipath numbers

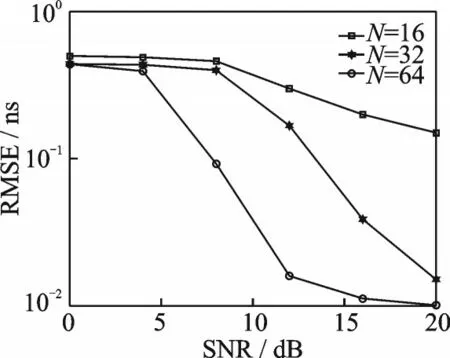
图6 本文算法在不同频点数下的TOA估计性能Fig.6 Estimated performance of the proposed algorithm for TOA at different numbers of frequency points

仿真3图7、8为本文所提算法与传统PM算法［12］、矩阵束算法［14］在不同信噪比下的参数估计性能比较，仿真参数设置与仿真1相同。由图7、8可以看出，本文所提算法在复杂度降低的情况下，还可以获得优于文献［12］中的矩阵束算法和文献［14］中的传统PM算法的TOA和DOA联合估计性能，并且随着信噪比的增大，所提算法的优势越来越明显，当信噪比达到12 dB时，所提算法的DOA参数估计误差的数量级迅速降低，这是因为当信噪比较大时，得到的DFT离散序列受噪声的影响变小，离散序列的稀疏性质显著提升，没有出现太大的能量泄漏效应，因此能够得到比较精确的TOA参数估计结果，DOA参数是根据TOA参数的估计结果计算出的，误差也较小。

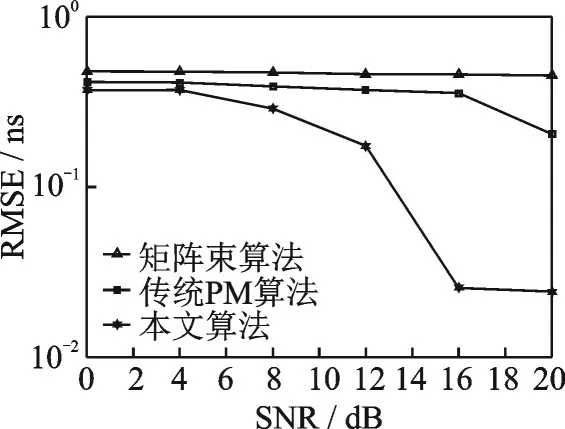
图7 3种算法在不同信噪比下的TOA估计性能比较Fig.7 Comparison of TOA estimation performance of three algorithms at different SNRs

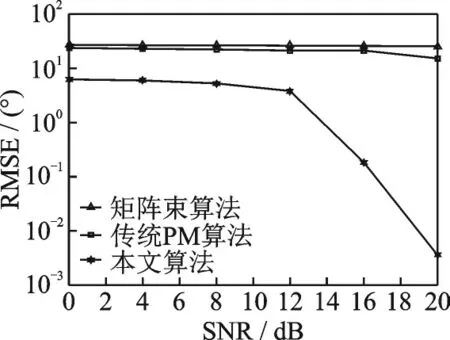
图8 3种算法在不同信噪比下的DOA估计性能比较Fig.8 Comparison of DOA estimation performance of three algorithms at different SNRs

仿真4图9，10为本文所提算法与传统PM算法［12］、矩阵束算法［14］在不同信号簇数K下的参数估计性能比较，仿真参数设置与仿真1相同。仿真结果表明，本文所提算法的TOA和DOA联合估计性能大大优于矩阵束算法和传统PM算法。由图9，10可以看出，随着信号簇数K的增大，矩阵束算法和传统PM算法的TOA和DOA估计误差变化不明显，而当K增加到300时，所提算法的TOA和DOA估计误差大大降低。当信号簇数K的值小于300时，所提算法的TOA和DOA的估计性能主要与信号簇数有关，下降较为明显，而当信号簇数K的值大于300时，所提算法的TOA和DOA的估计性能主要与除信号簇数外的其他参数有关，如信噪比和快拍数等，估计误差变化不明显。

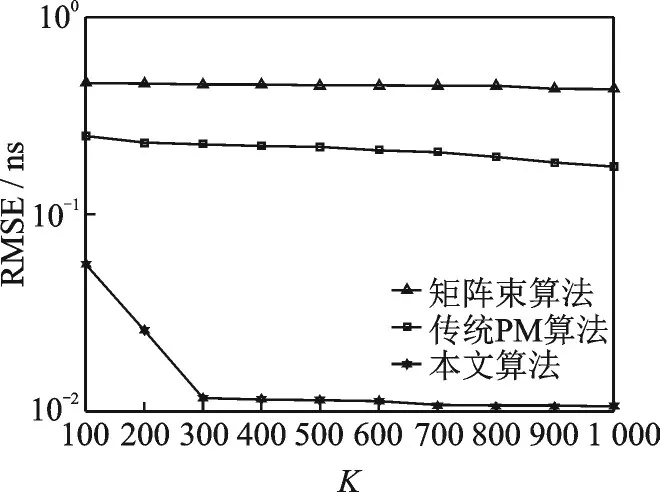
图9 3种算法在不同信号簇数K下的TOA估计性能比较Fig.9 Comparison of TOA estimation performance of three algorithms at different signal clusters

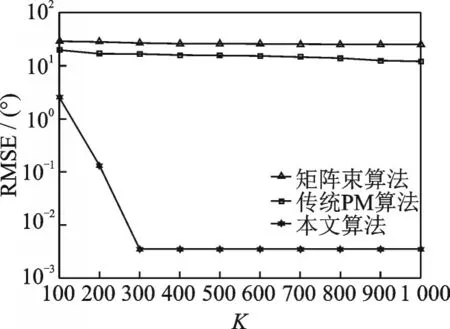
图10 3种算法在不同信号簇数K下的DOA估计性能比较Fig.10 Comparison of DOA estimation performance of three algorithms at different signal clusters

4 结束语

本文提出了一种基于DFT的TOA和DOA联合估计算法。算法对接收信号进行频域上的建模，计算得到频域接收信号的协方差矩阵，并对该矩阵进行DFT处理，从而得到两根天线的TOA粗估计结果。然后设计补偿矩阵对时延向量进行相位补偿，通过搜索得到粗估计结果的补偿值，根据粗估计结果和补偿值估计出精确的TOA参数。最后根据两根天线的到达时间差与DOA之间的关系得到信号的DOA估计值，从而实现TOA和DOA的联合估计。相比DOA估计中的谱峰搜索类算法，所提算法的粗估计过程受DFT点数影响，其估计精度有限。在高信噪比的条件下，信号簇数K的提升对TOA和DOA估计性能提升有限。本文所提算法无需复杂的特征值分解和广义逆求解步骤，复杂度低。仿真结果表明，本文所提算法具有较好的TOA和DOA联合估计性能，相比于矩阵束算法和传统PM算法，所提算法具有最小的参数估计误差，性能优越且易于实现。