基于Superbuck 变换器的光伏MPPT 调节器控制策略
2022-10-13方子文窦英华杨亚红付北南
方子文,窦英华,杨亚红,付北南
(上海空间电源研究所空间电源技术国家重点实验室,上海 222000)
在太阳电池和蓄电池的组合应用中,太阳电池通过充电调节器对蓄电池进行充电。为了提高太阳电池的能源利用率,变换电路通常采取最大功率点跟踪MPPT(maximum power point tracking)控制方式。常用的MPPT 功率调节变换器有降压型、升压型和升降压型。其中,Superbuck 变换器属于电流源型的降压电路,具有输入输出电流连续,输入输出电压极性相同,功率处理能力大,对母线及蓄电池造成的电流脉动较小等优点,适合作为蓄电池充电调节器,因此,广泛运用于航天用电源控制器PCU(power conditioning unit)系统中[1-4],从而提高MPPT的效率,降低电磁干扰EMI(electromagnetic interference)噪声的输入。
由于光伏发电机[5]的伏安特性曲线在一定区域内具有恒压或恒流特性,因此可以通过使用电压馈VF(voltage-fed)或电流馈CF(current-fed)转换器技术来实现MPPT 调节[6]。尽管文献[7-8]对MPPT 变换器技术进行了详尽调研,认为电压馈转换器在控制器中占主导地位,MPPT 变换器仍通常采取电流馈转换器,因为VF 变换器在光伏发电机模型中违反了基尔霍夫电流定律,造成最大功率点MPP(maximum power point)不稳定,从而限制了变换器在高于MPP 的电压下运行[9-10]。
本文应用对偶变换方法[11],研究了一种由相应的VF Superbuck 变换器[12]构造的CF Superbuck 变换器。应用状态空间平均法对CF Superbuck 变换器进行建模,设计双闭环控制策略;利用奈奎斯特频域稳定判据分析了所设计的光伏MPPT 调节器的稳定性,并讨论了滤波电感和电容对小信号稳定性的影响。最后,通过LTspice 仿真和实验验证了本文所提出的建模和控制方法的有效性。
1 光伏MPPT 调节器结构和原理
太阳电池-蓄电池组电源系统由太阳电池阵列功率调节,主要对蓄电池组进行充电调节控制、太阳电池阵列最大输出功率跟踪调节,并完成各主要性能参数的变换和控制。太阳电池阵列的输出接入功率调节电路,实现MPPT 输出,向后端蓄电池充电以及负载供电。系统采用蓄电池不调节母线,负载由一组高功率锂离子电池组供电。整个系统架构如图1 所示。
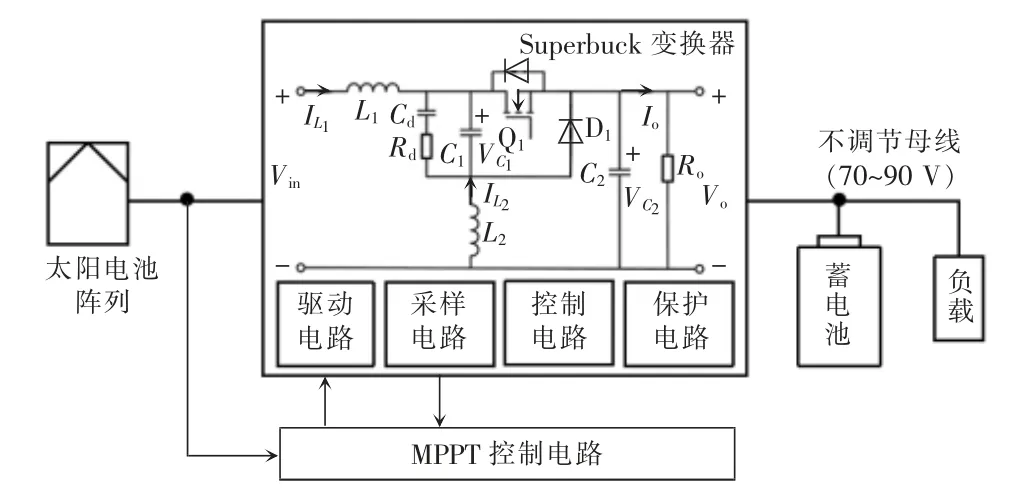
图1 光伏MPPT 调节器结构原理框图Fig.1 Block diagram of structural schematic of photovoltaic MPPT regulator
功率调节电路是含阻尼回路的独立电感型Superbuck 变换器,在中间电容C1两端引入RC 串联的阻尼回路,能够消除RHP 零点,改善高阶变换器的特性。其结构简单,不产生直流损耗,且成本较低。Superbuck 变换器具有与Buck 基本型变换器相同的电压变比,即

Superbuck 变换器主要工作波形如图2 所示。可以看出,输入侧电感L1的存在使得输入电流连续,在连续导通模式下,开关管Q1与二极管D1交替导通,所以输出电流也连续,且输出电压极性与输入电压极性相同。输出电流为电感L1和L2的电流之和。
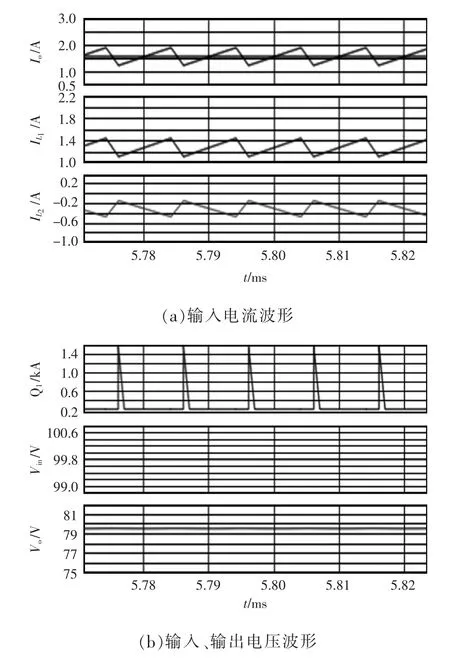
图2 Superbuck 变换器主要工作波形Fig.2 Main operating waveforms of Superbuck converter
2 CF Superbuck 变换器小信号建模
在MPPT 模式下,太阳电池阵列输出电压始终保持在最大功率点对应的电压附近,因此Superbuck 电路的输入端可认为是一个恒流源;此时负载功率需求大于太阳阵列所提供的电能,蓄电池以欠功率充电,Superbuck 电路的输出可等效为电压源。对Superbuck 电路进行小信号建模时,首先不考虑太阳电池阵列小信号模型,则MPPT 模式下Superbuck 的小信号模型如图3 所示。
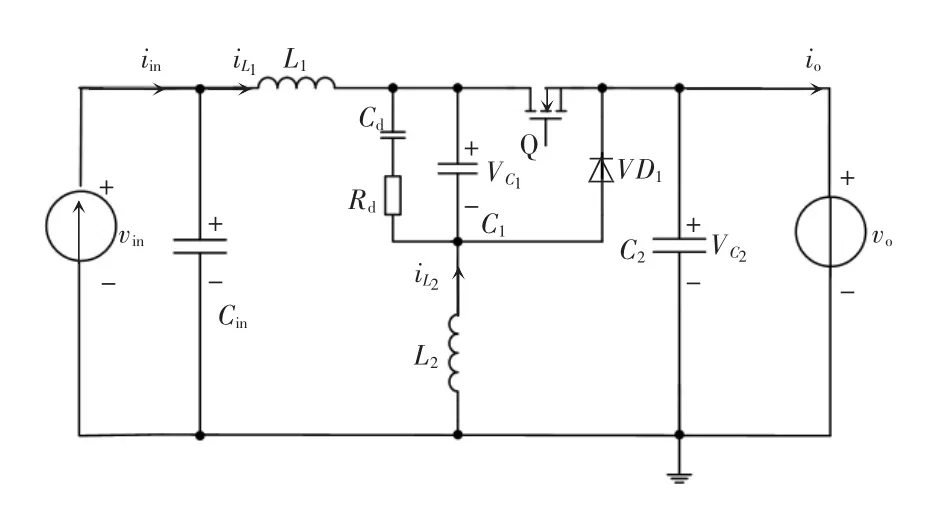
图3 Superbuck 变换器简化等效模型(MPPT 模式)Fig.3 Simplified equivalent model of Superbuck converter(MPPT mode)
当电路处于稳态时,任取一个开关周期进行分析。以电感电流iL1、iL2和电容电压vC1、vC2、vCd作为状态变量,输入电流iin和输出电压vo为输入变量,输出电流io和输入电压vin为输出变量,占空比d 为控制输入[4]。为建立状态空间方程,还考虑了输入和输出电容的ESR。将MOSFET 闭合和断开两个时间段的状态空间方程进行开关周期平均后求和,可得

根据电路关系,得到输入电压和输出电流为

在平衡点附近施加扰动量,消去状态平均方程两边的直流项并忽略二阶分量,可得到线性化后的小信号模型,即

根据状态空间方程和传递函数的转换关系,可以解得输出变量和输入变量之间的关系为

式中:Yo,o(s)为输出导纳;Gio,iin(s)为输入电流到输出电流的传递函数;Tvin,vo(s)为输出电压到输入电压传递函数;Zin(s)为变换器的开环输入阻抗;Gvin,d(s)为控制到输入电压的传递函数;Gio,d(s)为控制到输出电流的传递函数。
再考虑光伏电池等效模型,则可以得到传递函数的电路图法表示图,如图4 所示。
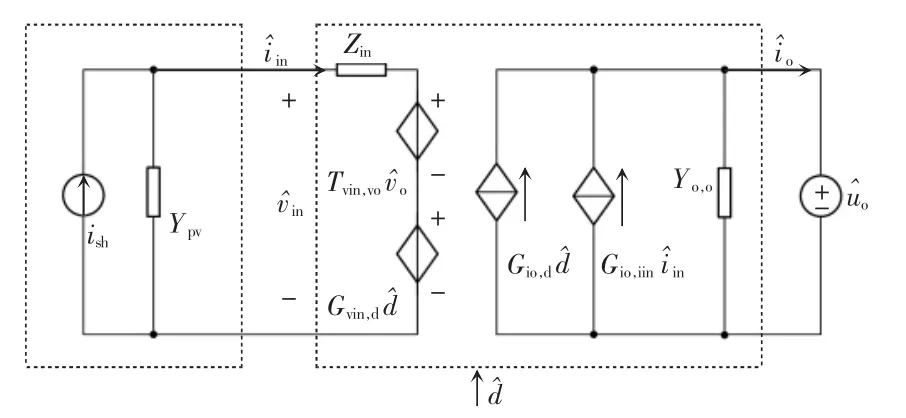
图4 Superbuck 变换器传递函数的电路图解Fig.4 Circuit diagram of transfer function of Superbuck converter
图4 中输入电流表示为
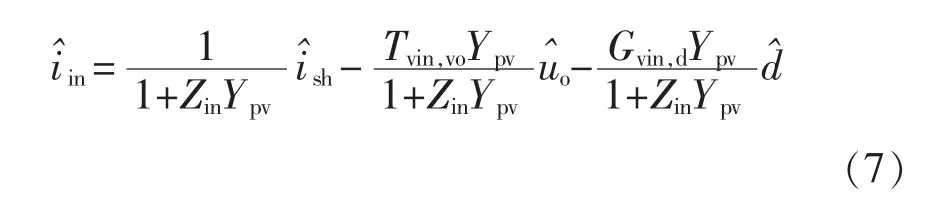
此时Superbuck 电路的状态方程为
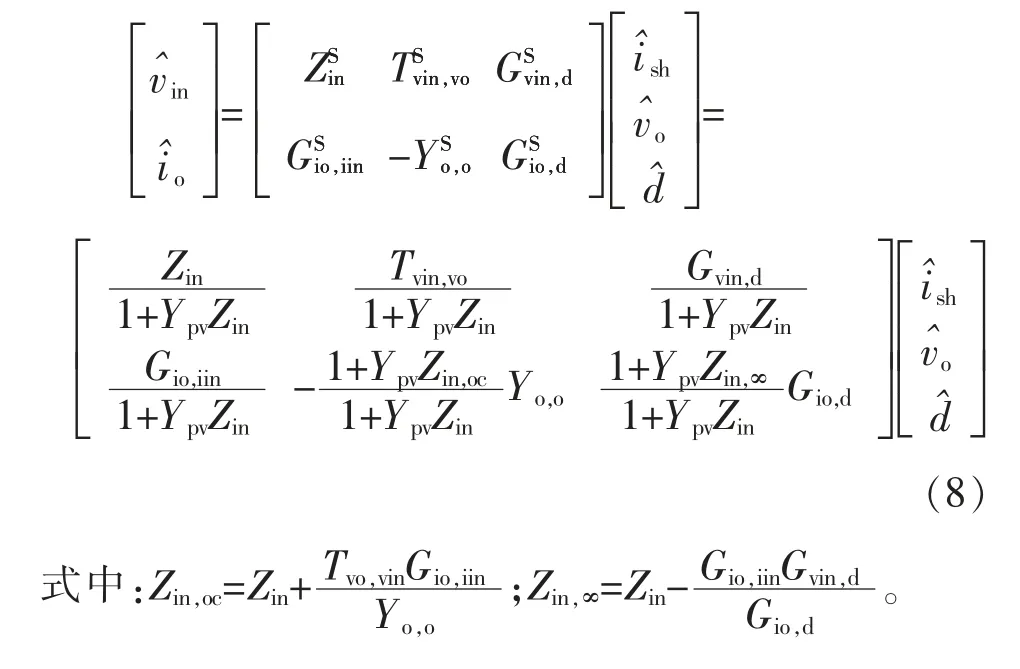
3 闭环控制策略设计和分析
Superbuck 变换器采用双环控制策略,分为MPPT 外环和输出电流内环。MPPT 外环控制输入端以最大功率给蓄电池快速充电,同时为了防止输出电流过大,加入限流环对输出电流进行限流。控制电路还包括输出电流采样电路、驱动电路等。
3.1 双闭环环路设计
采用平均电流控制的Superbuck 变换器双闭环控制框图如图5 所示,变换器的谐振特性受到包括电路寄生元件在内的传递函数的影响。其中,GPIu(s)和GPIi(s)分别为电压调节器和电流调节器的传递函数;KPWM 为PWM 调制器的传递函数;Gio,d(s)为占空比对于输出电流的传递函数;Gvin,io(s)为输出电流对于输入电压的传递函数;Hv为输入电压的采样系数;Hi为输出电流的采样系数;Vsaref为输入电压的参考信号;Ioref为输出电流的参考信号。Superbuck 变换器的主电路参数如表1 所示。电压调节器和电流调节器采用Ⅱ型补偿器,可产生90°相位抬升,其模型如图6 所示。

图5 Superbuck 变换器的双闭环控制框图Fig.5 Double closed-loop control block diagram of Superbuck converter
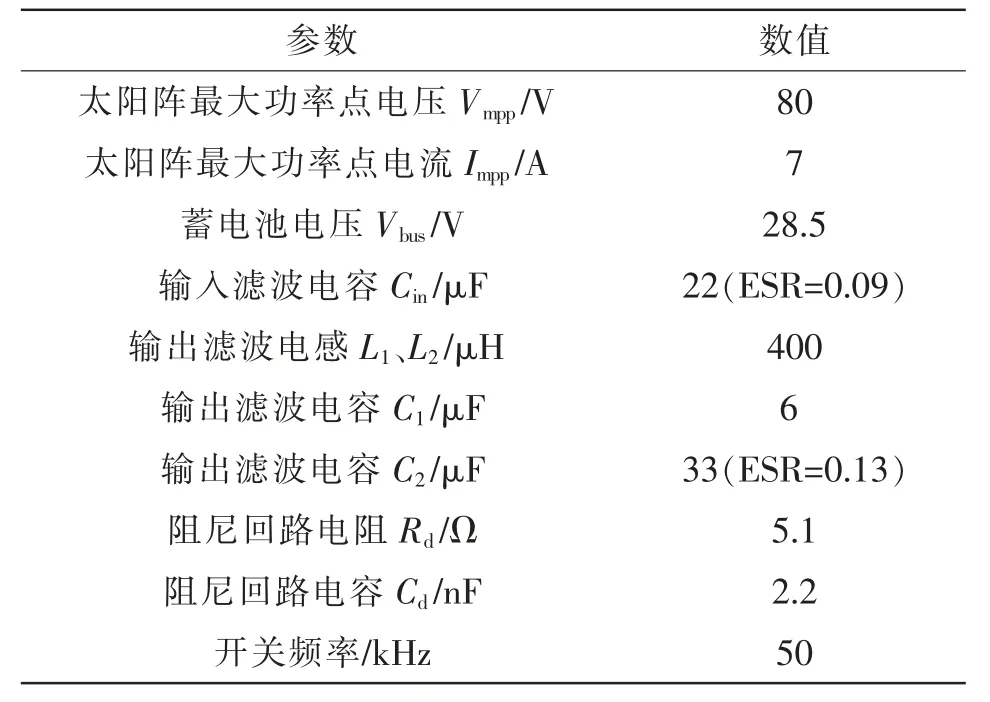
表1 Superbuck 变换器主电路参数Tab.1 Main circuit parameters of Superbuck converter
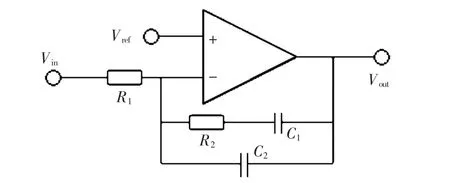
图6 Ⅱ型补偿器模型Fig.6 Ⅱ-type compensator model
Ⅱ型补偿器的传递函数为

为了使系统的动态响应更快,取电流内环的截止频率fc=20 Hz;为了抑制高频噪声,将高频极点fp设在开关频率fs处;为了提高低频增益,将低频零点fz设在0.01 fs处,联立得到
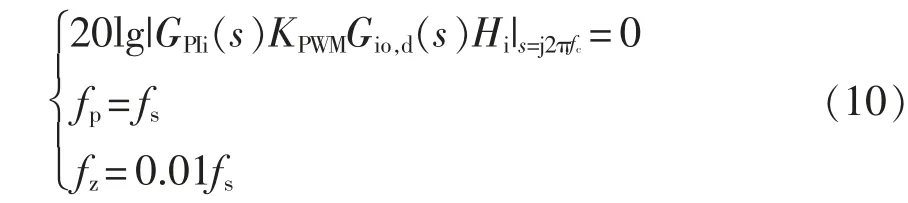
那么,Superbuck 变换器电流内环的等效功率级为
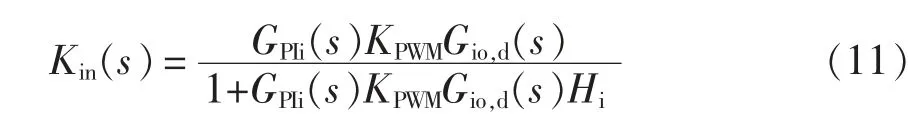
同理,取电压外环的截止频率fc=20 Hz;将高频极点fp设在0.2 fs处;将低频零点fz设在0.001 fs处,联立得到
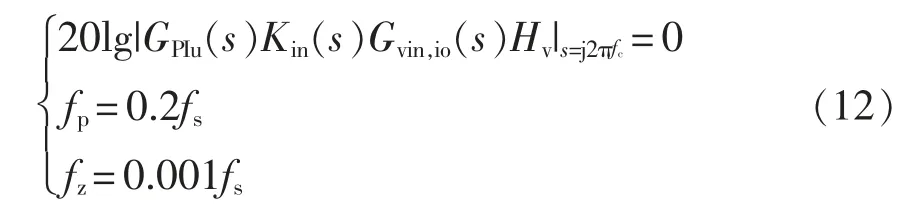
因此,设计电流内环补偿器的参数为Rin1=2 kΩ,Rin2=2 kΩ,Cin1=470 nF,Cin2=0.1 nF;设计电压外环补偿器的参数为Rout1=9.1 kΩ,Rout2=10 kΩ,Cout1=680 nF,Cout2=0.1 nF。
图7 为校正前后电流内环和电压外环的开环传递函数Bode 图。由图7(a)可以看出,补偿后电流内环的截止频率为20 Hz,相角裕度为75°,静态增益增大,稳态误差减小,电流闭环稳定性提高;由图7(b)可以看出,补偿后电压外环的截止频率为20 Hz,相角裕度为70°,稳态误差减小,电压闭环稳定性提高。

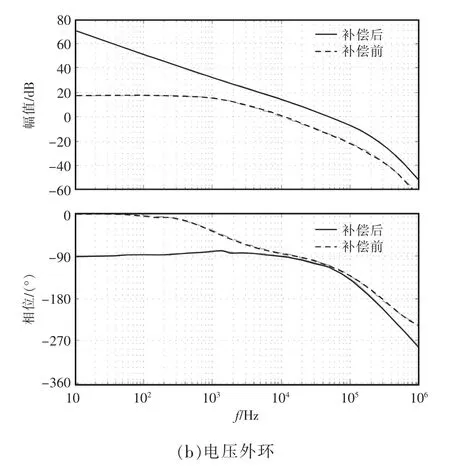
图7 校正前后电流内环和电压外环开环传递函数Bode 图Fig.7 Bode diagram of open-loop transfer function of inner current loop and outer voltage loop before and after correction
根据第2 节的小信号建模分析,给出输入电压控制下Superbuck 变换器开环和闭环的输入阻抗Bode 图,如图8 所示。

图8 开环和闭环变换器输入阻抗Bode 图Fig.8 Bode diagram of input impedance of open-loop and closed-loop converters
从图8 中可以看出,加入闭环控制后,变换器的输入阻抗在低频段得到了大幅衰减,有效提高了变换器的抗输入扰动特性,同时输入阻抗的相位保证了互联的光伏MPPT 系统将在光伏发电机的所有工作点上保持稳定,验证了闭环控制策略的有效性。
3.2 稳定性参数设计
光伏发电机的动态过程通常使得串联充电调节器所需的动态响应很低。因此,选择适当的电容器能够减小电压纹波,避免造成变换器功率损失或者EMI 噪声干扰。假设电感电流纹波很小,电容的峰间纹波电压可以表示为

由于控制传递函数中的右半平面(RHP)零点将把最大控制带宽限制在等于或小于RHP 零点的频率,当忽略寄生参数影响时有

为了避免其出现RHP 零点,应选择合适的电容比值,使得控制-输出传递函数Gio,d(s)的带宽远离谐振RHP 零点频率,即

4 实验验证
为了验证光伏MPPT 调节器的稳定性,采用LTspice 软件建立了Superbuck 变换器的仿真模型,并搭建了光伏MPPT 调节器原理样机进行实验验证,表2 给出了光伏MPPT 调节器的基本技术指标。仿真电路如图9 所示,信号回路包括MPPT 控制电路、采样电路、控制电路和驱动电路等。

表2 光伏MPPT 调节器基本技术指标Tab.2 Basic technical indexes of photovoltaic MPPT regulator

图9 光伏MPPT 调节器仿真电路Fig.9 Simulation circuit of photovoltaic MPPT regulator
图9 中MPPT 控制电路的作用是对太阳电池阵列进行最大功率跟踪。基本原理是对太阳电池阵列电压、电流进行交错扰动,在数次扰动后,太阳电池阵列的工作点将稳定波动在最大功率点附近。这种方法摒弃了传统算法中存在的大量乘除法运算,完全通过采样与小信号扰动完成,因此可以通过继承性更强的模拟电路实现。并且由于太阳电池阵列的输出特性,此算法还具有较快的追踪速度和较高的可靠性。
图10 示出了太阳电池阵列输入电流和输入电压交错扰动的仿真结果,算法每0.5 s 更新一次扰动,由于MPPT 控制是一种慢速控制,对输出端母线和负载电压的瞬态的稳定性提出了更高要求。

图10 太阳电池阵列输入电压和输入电流交错扰动仿真结果Fig.10 Simulation results under input voltage and input current staggered disturbance of solar cell array
如图11 所示,在波动过程中,实验测得的输出电压从28.5 V 下降到27.2 V,并在500 ms 内重新恢复到28.4 V。
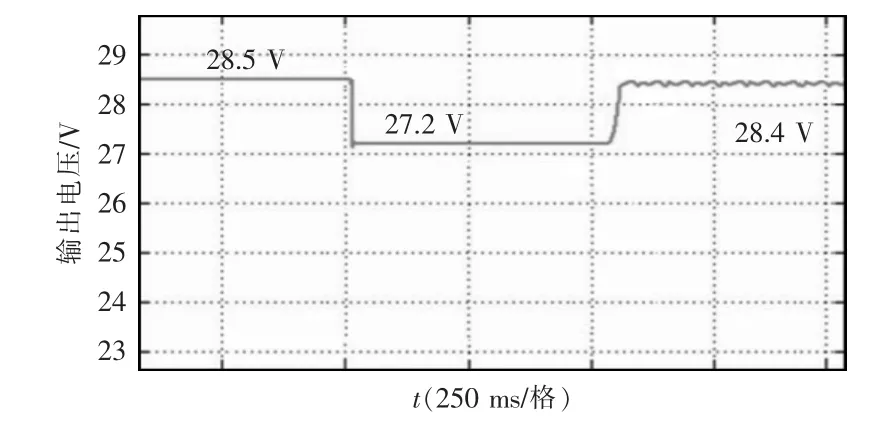
图11 扰动过程中的实测输出电压Fig.11 Measured output voltage during disturbance
设置仿真的太阳电池阵列最大功率点电压Vmpp=38.84 V,允许电压波动范围为±5%。如图12 所示,仿真得到的输入电压最终稳定在37.5~40.5 V之间波动,算法给出的MPPT 参考信号在3.6~4.2 V之间波动。
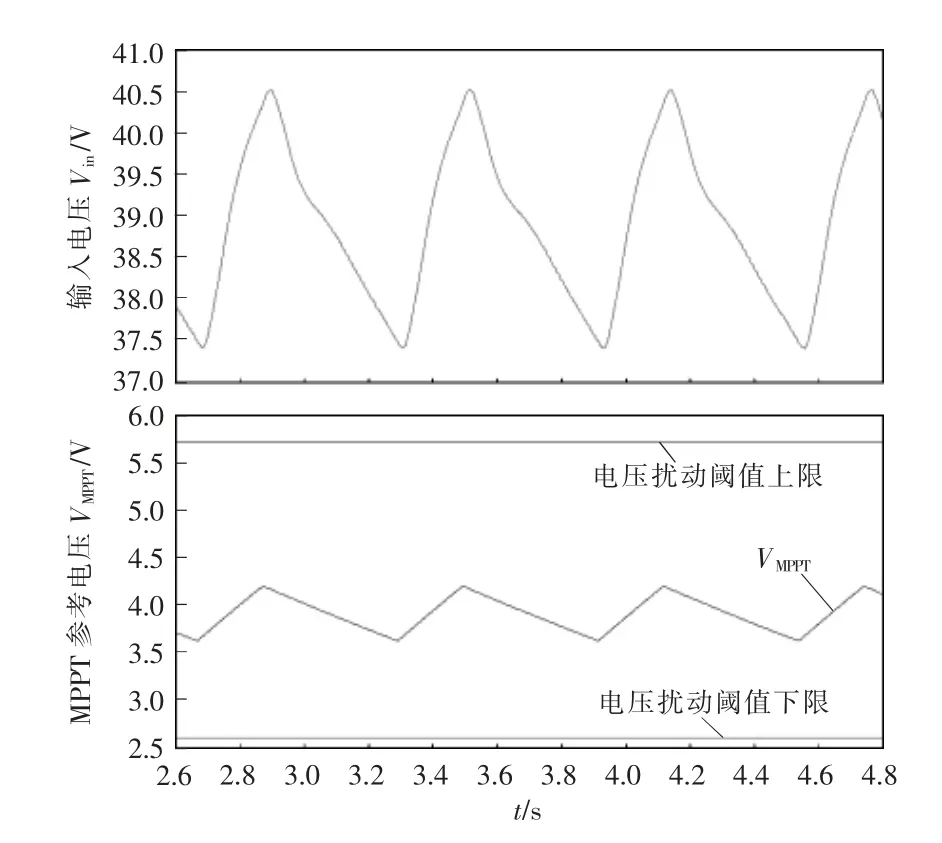
图12 太阳电池阵列输入电压和MPPT 参考值仿真结果Fig.12 Simulation results of input voltage and MPPT reference value of solar cell array
图13 示出了由示波器测得的光伏MPPT 调节器输入电压(Vin)和电流(Iin)波形。可以看出,输入电压的平均值为39.2 V,纹波的峰峰值约为4 V,与仿真结果十分吻合,MPP 电压跟踪误差为(39.2-38.84)/38.84=0.93%。实验表明,MPP 电压跟踪精度大于99%,所提出的控制策略能够对太阳电池阵列输出电压进行实时跟踪并调节,实现太阳电池阵列最大功率传输,提高了太阳电池阵列能量利用率。
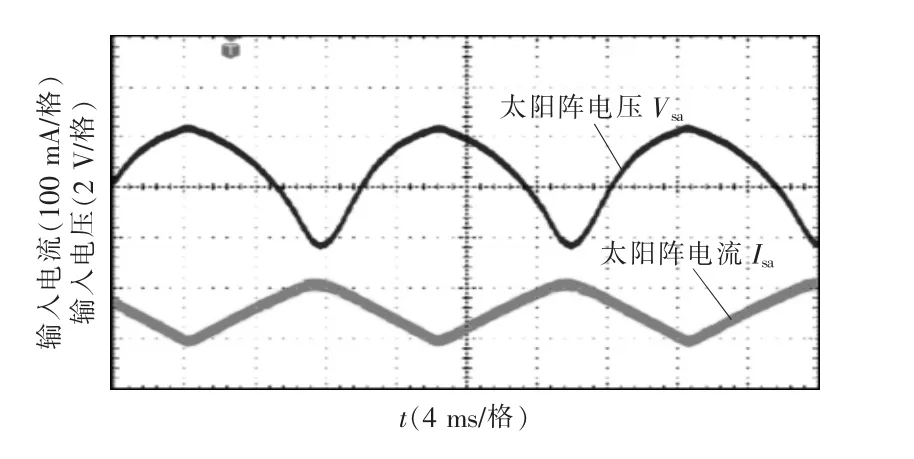
图13 太阳电池阵列输入电压和电流实际测量波形Fig.13 Actual measured waveforms of input voltage and input current of solar cell array
再将MPPT 的参考电压设置为固定值,观察MPPT 电路启动过程中输入电压和电流波形,如图14 所示。

图14 太阳电池阵列输入电压和电流启动波形Fig.14 Start waveforms of input voltage and input current of solar cell array
可以看出,电路的暂态过程持续约132 ms,电压超调量约为11.3 V,所设计的闭环负反馈能够满足电路对响应速率和稳定性的要求。
本文还给出了两个关键参数的实验测量结果,即功率跟踪精度和调节器的变换效率。表3 示出了太阳电池阵列模拟器在35~80 V 内不同伏安曲线的MPPT 实验测试结果,由于示波器的直流测量值存在一定偏差,表中为太阳电池阵列模拟器显示的数值。可以看出,在较宽的电压变化范围内,MPPT工作性能保持良好,功率跟踪精度大于98%。在最大功率(400 W)下,功率跟踪精度能够达到98.89%。图15 示出了光伏MPPT 调节器模块在输入电压38.8 V,3 种不同输出电压下的变换效率。可以看出,在电压不变的条件下,随着功率的增大,调节器的变化效率提高了至少1%。
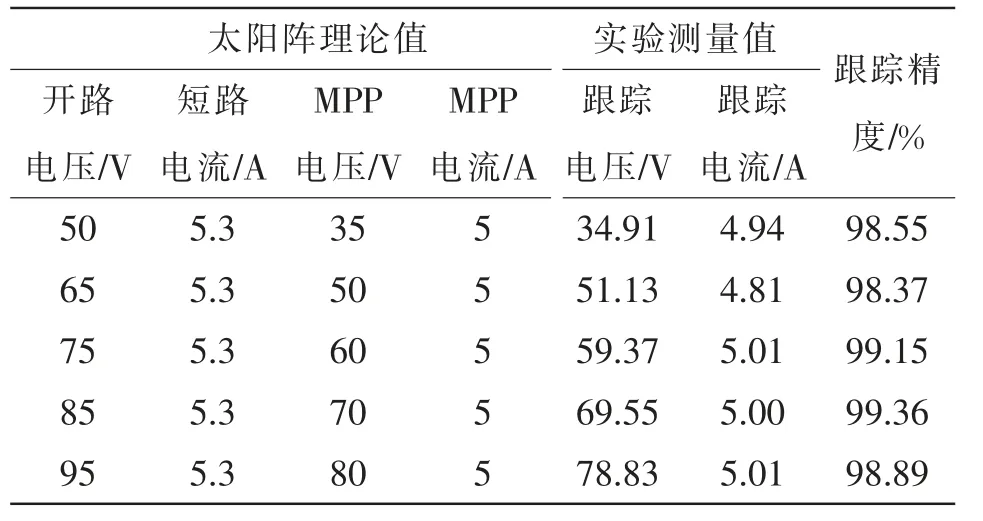
表3 MPPT 算法跟踪精度测试结果Tab.3 Test results of tracking accuracy when using MPPT algorithm
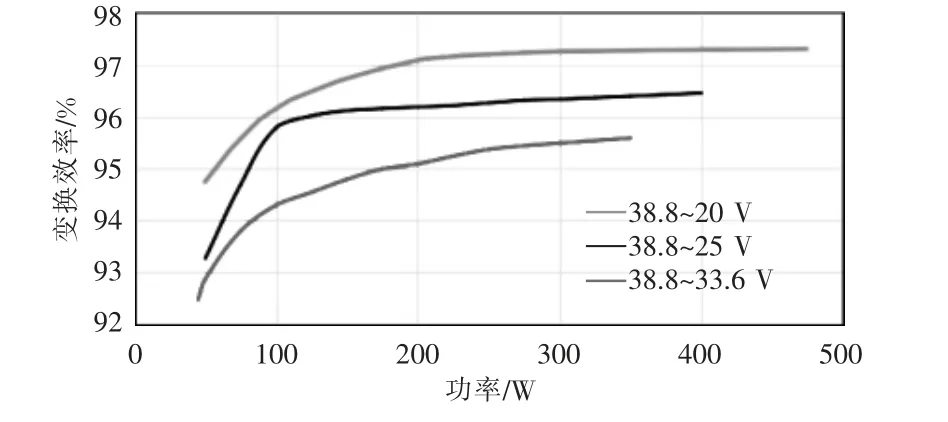
图15 模块效率Fig.15 Module efficiency
5 结论
本文基于Superbuck 变换器搭建了一种应用于航天器光伏变换系统的MPPT 调节器。通过状态空间平均法对变换器进行小信号建模,并基于MPPT 模式提出了太阳电池阵列电压控制的双闭环控制策略。实验验证了所提出的光伏MPPT 调节器具有良好的稳定性,并且MPPT 精度达到99%,提高了太阳电池阵列的能源利用率,普遍适用于具有宽范围输入、输出电压要求的降压类电源控制器。
以本文的设计为基础,后续将从以下方面继续深入研究:①增加必要的硬件故障保护功能,对输入、输出电流保护电路进行设计,避免母线过流对变换器造成损害;②MPPT 算法跟踪精度很大程度上取决于采样电压、电流的准确性,需要改进输入、输出电流检测方法,以提升MPPT 的变换效率;③为了避免单点失效,需要对MPPT 电路进行多路并联的冗余设计,进一步提高调节器的可靠性。
