典型驾驶操作行为识别及表征模型研究*

贾丙硕 金建虎 何子钦

（1-陕西工业职业技术学院 陕西 咸阳 712000 2-长安大学汽车学院）

引言

随着中国经济的快速发展，中国的汽车和交通行业发生了巨大的变化，汽车和驾驶人的数量急剧增加，随着机动车驾驶人数量的迅速增加，道路交通安全隐患是我们必须面对的一个重大问题，驾驶人是车辆的操纵者[1]，其驾驶行为是影响交通安全的最重要因素之一[2-4]。因此，对驾驶行为的研究对于预防交通事故、促进智能交通和未来驾驶辅助系统的发展具有重要意义。

国内外交通安全研究对驾驶人这一影响因素高度关注[5-6]，Liuyun 提出使用P-2dHmm 模型进行驾驶行为识别，该模型的输入为汽车的速度、纵向加速度和空间，输出为驾驶行为作为[7]；Berndt 等人基于车辆传感器数据特征向量对驾驶人的驾驶行为进行识别，然后基于隐马尔科夫模型计算出特定驾驶行为的输出概率，在此基础之上，基于驾驶人当前的驾驶行为修正概率，从而实时识别车道偏离和跟随行为[8]；清华大学的何长伟在车内构建了分布式网络，将车内实际状态转化为对应的信息和数字，建立了数据模型，为汽车驾驶操作行为的识别奠定了坚实的基础[9]。当前，对驾驶行为分析的研究已经迅速成为一个研究热点，许多研究机构相继建立驾驶行为研究的实验环境[10-12]，但是实车实验相对较少，多为仿真环境。国内外对驾驶行为的研究多为对异常驾驶行为的识别和驾驶意图等方面的研究[13-14]，鲜有人对驾驶人正常驾驶行为模式进行深入研究。

因此本文从车载智能终端记录下的GPS、视频监控系统和从CAN 总线采集的数据出发，通过数据挖掘，重点研究车辆驾驶人典型纵向驾驶操作行为识别方法和变化规律，并基于隐马尔科夫理论建立驾驶人行为模式表征模型。

1 典型纵向驾驶操作行为识别

1.1 驾驶人行为分析

驾驶人行为识别就是通过数据分析提取车辆运动学特征从而可以准确有效地识别驾驶人行为。本文将主要从CAN 总线数据出发动态识别驾驶人的快减速、慢减速、速度保持、慢加速、快加速和停止行驶6 种典型纵向驾驶操作行为。

通过对普通城市道路、城市高速道路和高速公路环境下驾驶人驾驶车辆的实验，从CAN 总线获取驾驶人行车时的速度、加速度数据，并通过视频监控系统记录整个过程。观看实验录像，结合GPS 数据，将实验道路划分为高速公路、普通城市路段和城市交叉口路段三种不同的路段，获得三种不同路段下驾驶人的速度和加速度数据。

1.2 试验设计

本研究选取了包括普通城市道路、城市高速道路和高速公路等试验路线反馈回来的数据，路试第一部分为湖州市的一段公路，第二段路试在西安市进行，所有数据来源于大众途安2.0 自动挡多功能轿车试验车。本文主要采用车载CAN 记录仪所采集到的数据（GPS 数据作为辅助）进行典型纵向驾驶行为识别和驾驶行为规律分析，用到的项目有时间、车速和加速踏板开度。

本次研究使用的数据为湖州实验12 位驾驶人和西安实验25 位驾驶人的实验数据，他们年龄在23至54 岁之间（M=39.4 岁，SD=8.0 岁）。他们拥有2至24 年（M=10.86 岁，SD=5.72 岁）和平均10.9 年的驾驶经验。其中M 表示平均值，SD 表示标准差。

1.3 阈值确定

本研究将结合实际情况和有经验的驾驶人以及交通行业专家的建议，最终确定将37 位被试驾驶人的加速度分别从小到大排序（注意这里区分正负号），计算出每位驾驶人20%、30%、40%、50%、60%和70%位的减速度和加速度，并对37 位被试驾驶人的相应位的加速度和减速度平均，最终确定快减速、慢减速、保持速度、慢加速、快加速的分类标准。

1.4 数据处理

1.4.1 数据平均处理

为了保证采集速度的精确性，本实验所用到的频率为100 Hz，考虑到驾驶操作行为的特点，驾驶人在一秒内不会完成几个加减速操作，故本研究将速度时间间隔定为1 s，为避免每秒内数据突变对分析结果有较大影响，计算得到37 位驾驶人对应的每秒速度数据的方差均小于0.12 km/h，可见直接对每秒的数据做平均对分析结果无太大影响。用MATLAB 程序计算速度每秒的平均值，处理结果如表1 所示。

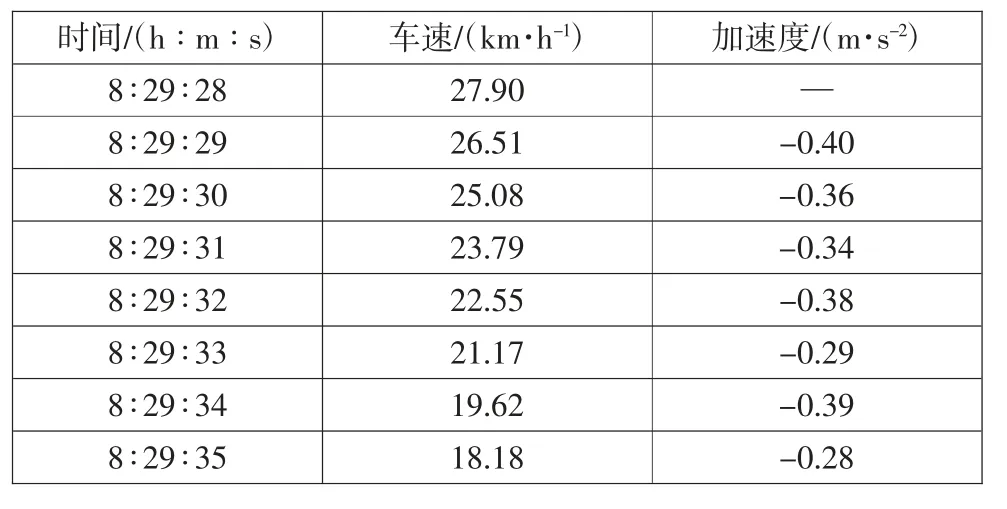
表1 加速度计算结果

1.4.2 加速度计算

正常驾驶人在行车过程中，驾驶比较平稳，一般情况下加速度会保持匀加速或匀减速状态，故而一般情况下，速度不会发生突变。但是考虑到会有紧急情况的出现，紧急情况下速度在短时间内可能会变化幅度较大，因此在本文中计算加速度时，时间间隔取1 s，采用式（1）

式中：V1为汽车初速度，单位为m/s；V2为汽车末速度，单位为m/s；t1为起始时刻，单位为s；t2为 结束时刻，单位为s

计算出加速度后，按照1.3 节典型驾驶操作行为方法确定出加速度分段的阀值。处理结果如表2 所示，对37 位驾驶人的数据采用相同的方法处理后，汇总并取平均，参照各驾驶人速度和加速度数据，最终确定取加速度30%位和70%位加速度值为加减速阈值结果如表3 和表4 所示。

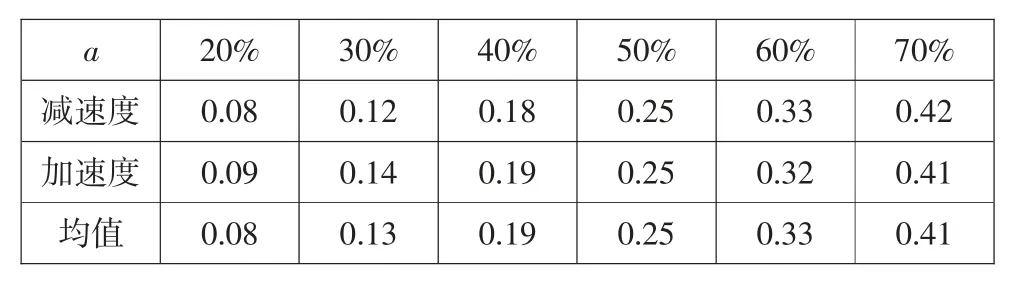
表2 某驾驶人各百分位加减速度 m/s2

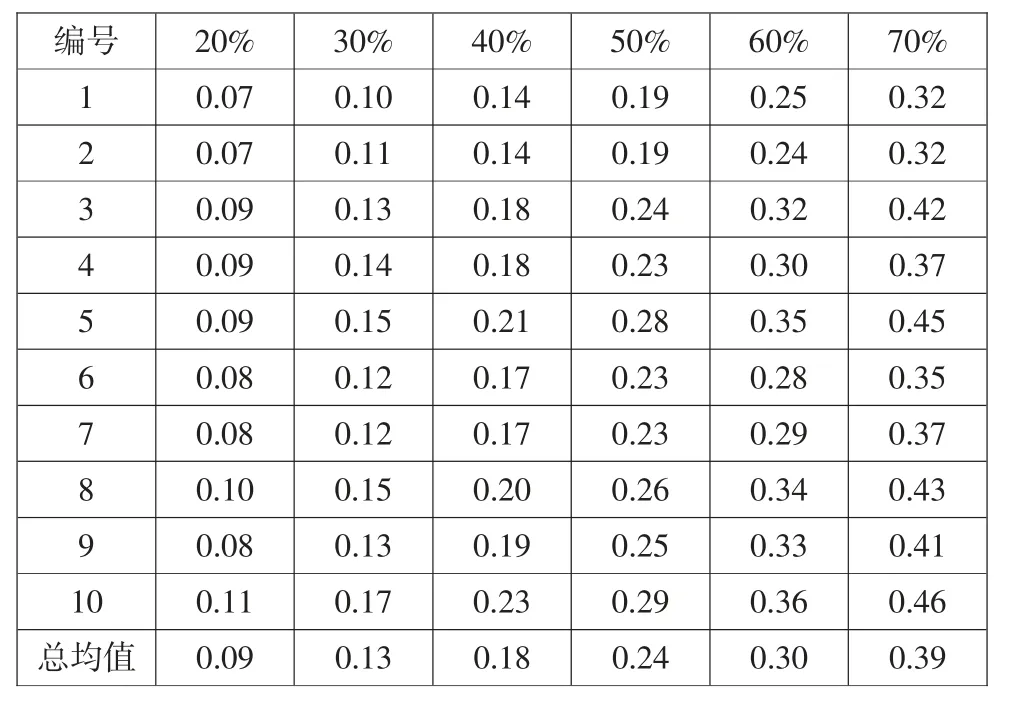
表3 部分驾驶人加速度阈值预选 m/s2

表4 加速度阈值 m/s2

1.4.3 典型纵向驾驶操作行为动态识别

根据所划定的加速度阈值，总结识别驾驶人驾驶行为的检测方法：若a ＜-0.39 m/s2,则识别为快减速；若-0.39 m/s2≤a ＜-0.13 m/s2，则识别为慢减速；若-0.13m/s2≤a ＜0.13m/s2，则识别速度保持；若0.13m/s2≤a ＜0.39 m/s2，则识别为慢加速；若a≥0.39 m/s2，则识别为快加速；而当加速度为0 且速度为0，则识别为停止行车。同时给识别的结果进行编号。若为快减速，则对应编号为1；若为慢减速，则对应编号为2；若为速度保持，则对应编号为3；若为慢加速，则对应编号为4；若为快加速，则对应编号为5；若为停止行驶，则对应编号为6。

2 驾驶行为模式表征模型建立

2.1 隐马尔科夫理论

隐马尔科夫模型由初始概率分布、状态转移概率分布以及观测概率确定。设Q 是所有可能的状态的集合，V 是所有可能的观测的集合。

式中：N 为可能状态数；M 为可能的观测数。

状态转移矩阵A：

式中：aij=p（it+1=qj∣it=qi）；j=1，2，…，N；i=1，2，…，N 表示在时刻t 处于状态qi的条件下在时刻t+1 转移到qj的概率。

观察概率矩阵B：

式中：bj（k）=P（Ot=vk∣it=qj）；k=1，2，…，M；j=1，2，…，N 表示在时刻t 处于qj的条件下生成观测vk的概率。

初始状态概率向量π：

式中：πi=P（i1=qi）；i=1，2，…，N 表示时刻t=1 处于状态qi的概率。

2.2 驾驶行为表征模型

在不同的道路类型上，驾驶人的驾驶操作行为存在不同的规律。道路类型和驾驶操作行为顺序构成马尔科夫链。道路类型为状态序列，与其对应的驾驶行为操作为观察序列，建立一个隐马尔科夫模型。为了方便研究，将高速路段、普通路段和交叉口路段分别编码为1、2 和3，然后从MATLAB 隐马尔科夫工具箱中调用hmmestimate 函数，得到所有被试驾驶人的状态转移矩阵trans 和输出矩阵emis。

平均指标可以反映现象总体的综合特征，也可以反映分配序列中各变量值分布的集中趋势。标准差可以衡量一组数据的离散程度。将所有驾驶人的状态转移矩阵数值进行平均和求标准差得到下式：

从上式中可以看出高速-高速、普通-普通、交叉口-交叉口的转移概率平均值都在97%以上，所有标准差结果都非常小，最大的为0.006 1。为了更加直观地看出路段转移矩阵的规律，制作如图1 和图2 所示。

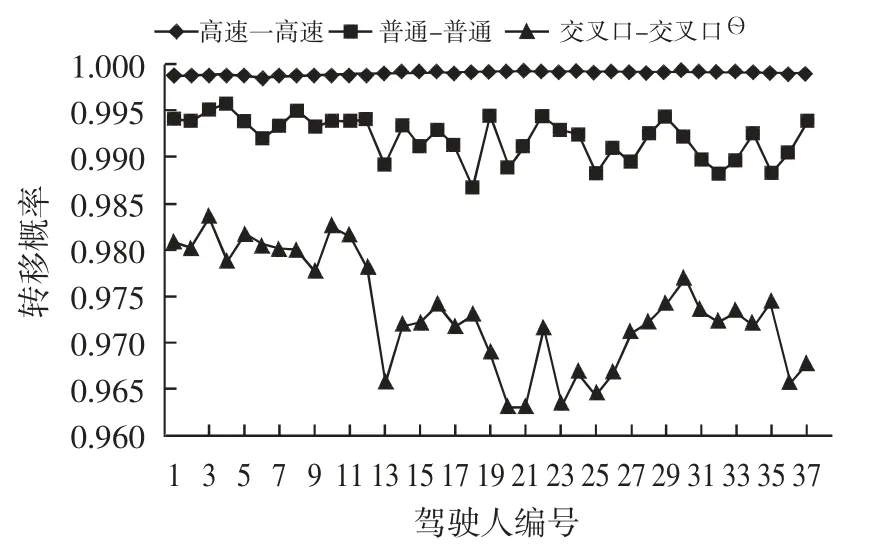
图1 高速-高速、普通-普通和交叉口-交叉口转移概率图

图2 高速-普通、普通-高速和交叉口-普通转移概率图

依据上图可以看出，各路段转移概率的大小依次为：高速-高速、普通-普通、交叉口-交叉口、交叉口-普通。高速-普通和普通-高速的概率基本相等且非常小，接近于0（但不等于0）。其中图中没有高速-交叉口和交叉口-高速的概率曲线。出现此规律的原因其实不难解释，此规律符合实际情况。因为：

1）在实验路段只有一段高速路段且是连续的，所以在路段转移过程中，高速-普通只有一次，普通-高速也只有一次，是在上高速和下高速的时候。

2）在行驶路线中，高速路段和普通路段占比很高，观察序列长度都在3 000 左右，所以在车辆行驶过程中基本是在高速-高速和普通-普通的转换。

3）在行驶线路中，交叉口的个数只有二十几个，所以普通-交叉口和交叉口-普通就转换了二十几次，分别是在进交叉口和出交叉口的时候。

2.3 输出矩阵分析

根据驾驶行为表征模型输出矩阵结果，高速路段、普通路段和交叉口路段下驾驶人驾驶行为操作输出概率如图3、图4 和图5 所示。

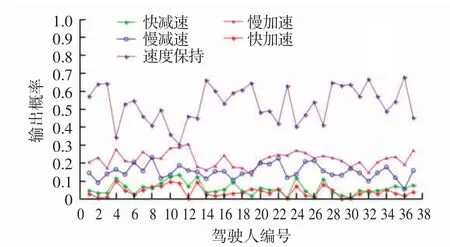
图3 高速路段驾驶人驾驶行为操作输出概率图

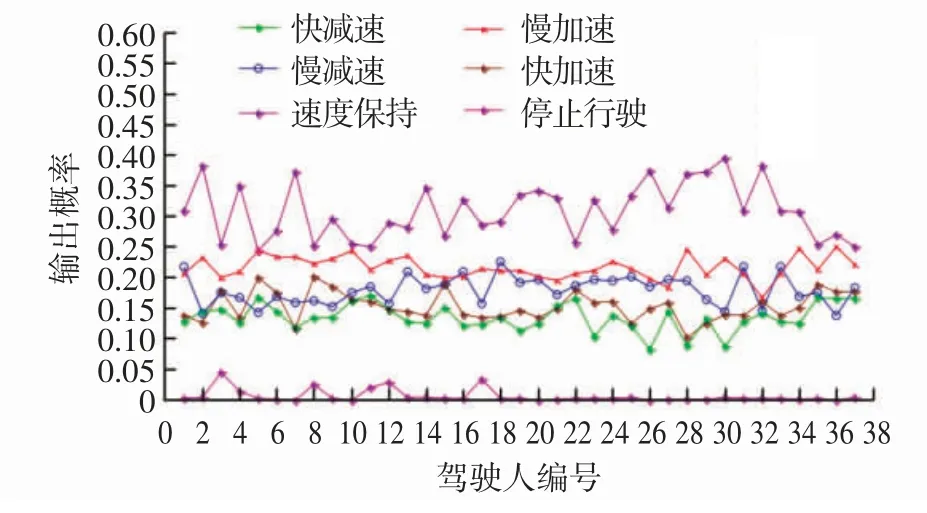
图4 普通路段驾驶人驾驶行为操作输出概率图

从图3 可以看出每位驾驶人在高速路段出现的操作行为概率基本为速度保持、慢加速、慢减速、快减速、快加速。其中出现速度保持的概率除极个别（4、11）外都在40%以上；出现慢加速的概率基本都在10%～30%之间，出现慢减速的概率绝大部分在10%～20%之间；出现快减速操作的概率都在15%以下，绝大部分在10%以下；出现快加速的概率都在10%以下。

从图4 可以看出每位驾驶人在普通路段出现速度保持的概率最大，基本都在25%～40%之间；出现慢加速的概率都在15%～25%之间，除极个别（27、32）外都在19%～25%之间；出现慢减速的概率都在14%～25%之间；出现快减速的概率在7%～18%之间；出现快加速的概率在10%～20%之间。绝大多数人出现停止行驶的概率为接近或等于0，个别不为0 的也在5%以下，其中湖州路线出现停止行车的概率较西安路线大，但是差别很小，这是因为湖州实验路线比西安实验路线拥堵程度略高一点。

依据图5 可以看出：（前12 位为湖州被试驾驶人，后面都为西安被试驾驶人）湖州路线和西安路线的操作行为规律大致相同，但是在数值上还是有些差别，所有驾驶人在交叉口路段表现出：

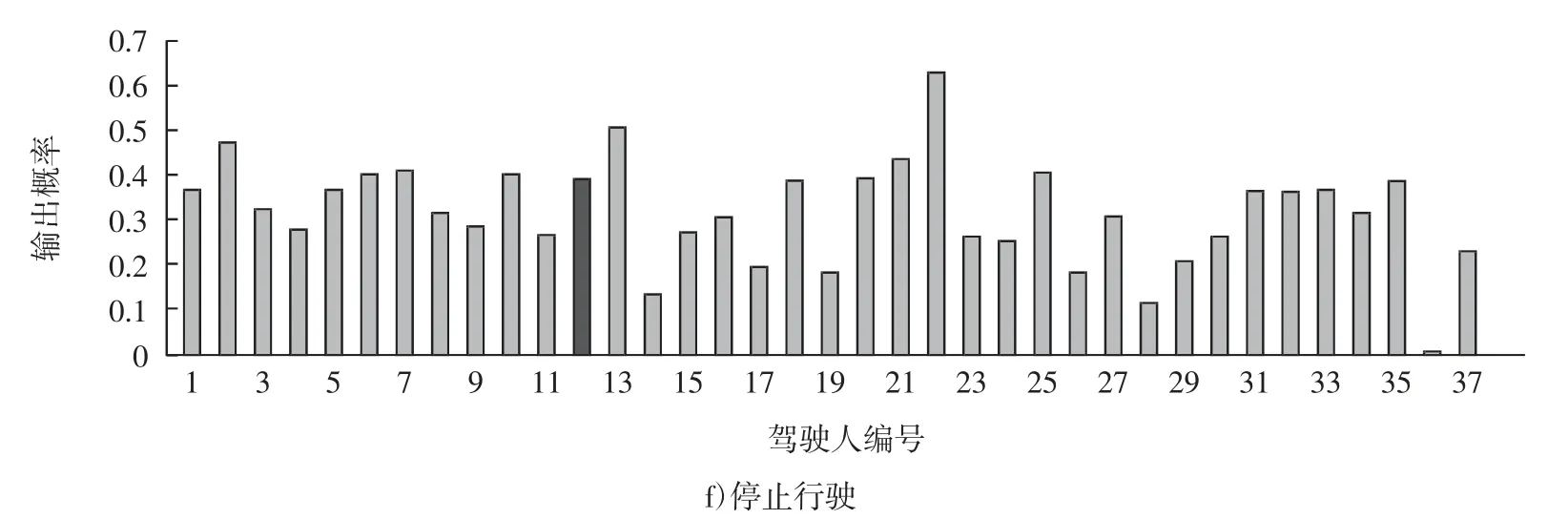
图5 交叉口路段各驾驶操作行为输出概率图

1）出现快减速操作的概率都在25%以下，总体上湖州路线的概率略高于西安路线的概率，湖州路线大部分在15%～25%之间，西安路线绝大部分在5%～25%之间。

2）出现慢减速操作的概率，总体上湖州路线略小于西安路线。湖州路线都在10%以下，绝大部分都在5%～10%之间；西安路线都在20%以下，绝大部分在10%～15%之间。

3）出现速度保持的概率，总体上湖州路线略小于西安路线。其中湖州路线都在15%以下，除1 号外都在10%以下。西安路线基本上都在10%～30%之间。

4）出现慢加速的概率，总体上湖州路线略低于西安路线。湖州路线都在15%以下，其中绝大部分在10%以下。西安路线都在20%以下，其中绝大部分不小于10%。

5）出现快加速的概率，总体上湖州路线略高于西安路线。湖州绝大部分在20%～30%之间，西安路线绝大部分在10%～20%之间。

6）出现停止行车的概率，两段路线基本都在50%以内，湖州路线比西安路线停止行车概率稍高一点，但不太明显。

3 结论

本文在前人研究的基础上提出了对典型纵向驾驶行为的识别方法，并基于驾驶人在不同道路类型驾驶数据基于隐马尔科夫理论建立了驾驶人典型驾驶行为表征模型，研究发现：

1）基于实车实验确定了正常驾驶人加速度阈值，确定了a ＜-0.39 m/s2为快减速，-0.39 m/s2≤a ＜-0.13 m/s2为慢减速，-0.13 m/s2≤a ＜0.13 m/s2为速度保持，0.13 m/s2≤a ＜0.39 m/s2为慢加速；a≥0.39 m/s2为快加速；而当加速度为0 且速度为0，则为停止行驶。进而提出了对典型纵向驾驶行为动态识别的方法。

2）在同一道路上不同驾驶人的状态（道路类型）转移概率基本是一致的，并且相同路段类型之间的转移概率最大。

3）高速路段出现速度保持的概率最高，明显高于其它两种路段，其次为普通路段。三种路段出现快减速和快加速操作的概率为高速路段＞普通路段＞交叉口路段；交叉口路段出现停止行车的概率最大，高速路段为0。