斜逆洛朗级数环的弱McCoy性*

王尧，史叶萍，任艳丽

1. 南京信息工程大学数学与统计学院，江苏 南京 210044

2. 南京晓庄学院信息工程学院，江苏 南京 211171

1 (σ，δ)-SILS 右弱McCoy环的刻画

以下，我们以nil(A)表示一个环A的所有幂零元素构成的集合。

定义2设R是一个环，σ是R上的一个自同构，δ是环R的一个σ-导子，那么称环R是一个线性(σ，δ)-SILS 右弱McCoy 环，如果对任意f(x) =a-1x-1+a0，g(x) =b-1x-1+b0∈R((x-1；σ，δ)){0}且满足f(x)g(x) = 0，则存在非零元c∈R使得aixic∈nil(R((x-1；σ，δ)))，其中i，j∈{0，- 1}.

易见，(σ，δ)-SILS右弱McCoy环一定是线性(σ，δ)-SILS右弱McCoy环；(σ，δ)-SILS右McCoy环一定是(σ，δ)-SILS 右弱McCoy 环。但反过来未必成立（见例1）。当R((x-1；σ，δ))是约化环（没有非零的幂零元）时，两者相同。

例1设R是一个约化环，令S=T2(R)表示R的2阶上三角矩阵环，则S是(1，0)-SILS右弱McCoy环，但不是(1，0)-SILS右McCoy环。

证明 根据下面的定理2知S是(1，0)-SILS右弱McCoy环。令

推论1设R是一个约化环，Mn(R)表示R上的n阶矩阵环，其中n≥2. 则Mn(R)不是(1，0)-SILS 右弱McCoy环。

证明 文献［8］的命题1.1 证明了Mn(R)不是幂级数右弱McCoy 环，可以类似证明Mn(R)不是负幂级数右弱McCoy环，再由引理1，Mn(R)更不是(1，0)-SILS右弱McCoy环。

例2设R是一个环，Tn(R)表示R的n阶上三角矩阵环，则Tn(R)是负幂级数右弱McCoy 环，但Tn(R)不是负幂级数右McCoy环。

证明 根据文献［8］的例1.1，可以同理证得。

所以，S不是负幂级数弱Armendariz 环。根据文献［8］的例1.2，知Tn(S)不是负幂级数弱Armendariz 环，因此也不是一个（1，0）-SILS弱Armendariz环。

若一个环R是(σ，δ)-SILS右弱McCoy环，下面考虑它关于环同构是否封闭。

命题2设R是一个环，σ是R上的一个自同构，δ是环R的一个σ-导子。设S为一个环且存在环同构γ：R→S，则R是(σ，δ)-SILS右弱McCoy环当且仅当S是(γσγ-1，γδγ-1)-SILS右弱McCoy环。

证明 令σ′=γσγ-1，δ′=γδγ-1. 易得σ′是环S上的自同构，下证δ′是S的一个σ′-导子。对任意a，b∈S，由

知δ′是S的一个σ′-导子。

下证当R是(σ，δ)-SILS右弱McCoy环时，S是(γσγ-1，γδγ-1)-SILS右弱McCoy环。

推论3设R是一个环，σ是R上的一个自同构，δ是环R的一个σ-导子。e∈R是一个中心正则幂等元且满足σ(e) =e，δ(e) = 0，则下列命题等价：

（i）R是一个(σ，δ)-SILS右弱McCoy环；

（ii）eR（Re）是一个(σ，δ)-SILS右弱McCoy环；

（iii）(1 -e)R（R(1 -e)）是一个(σ，δ)-SILS右弱McCoy环。

证明 （i）⇔（ii） 因为e∈R是中心的，所以eR=Re，再由命题3即证。

文献［11］给出了弱-相容的概念。设σ是环R的一个自同态，如果对于任意a，b∈R，ab∈nil(R) ⇔aσ(b) ∈nil(R)，就称σ是弱-相容的。如果环R存在一个弱-相容的自同态σ，则称环R是弱σ-相容的。设δ是一个σ-导子，如果对于任意a，b∈R，ab∈nil(R) ⇒aδ(b) ∈nil(R)，则称环R是弱δ-相容的。如果一个环R既是弱σ-相容的又是弱δ-相容的，则称R为弱(σ，δ)-相容环。我们在文献［10］中将弱(σ，δ)-相容环的部分性质进行了推广，得到以下结论。

引理3[10］若R为弱(σ,δ)-相容环，则有

（i）ab∈nil(R) ⇔σm(a)σn(b) ∈nil(R)，对任意m，n∈Z.

（ii）ab∈nil(R) ⇒σm(a)δs(b)，δt(a)σn(b) ∈nil(R)，对任意m，n∈Z，s，t∈N.

定理1设R是弱(σ，δ)-相容环且nil(R)是幂零理想，那么以下结论成立且是等价的：

（i）R是(σ，δ)-SILS右弱McCoy环。

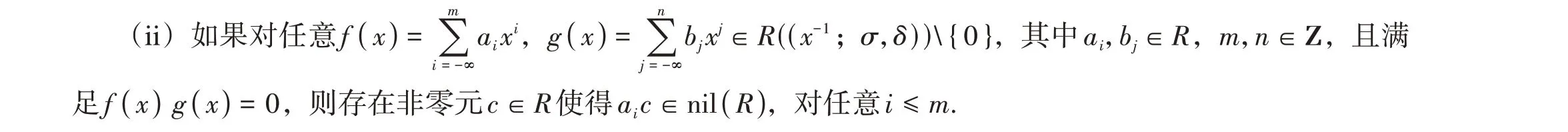
证明 结论成立是显然的，下证两个命题是等价的。

（i）⇒（ii）设f(x)，g(x)是满足（ii）中要求的幂级数。因为R是(σ，δ)-SILS 右弱McCoy 环，则一定存在0 ≠c∈R满足aixic∈nil(R((x-1；σ，δ))). 根据文献［10］的命题3 可得aixic∈nil(R) ((x-1；σ，δ))，再由文献［10］的命题4，有aic∈nil(R).

（ii）⇒（i）已 知 存 在 非 零 元c∈R满 足aic∈nil(R)， 对 任 意i≤m. 那 么 根 据 引 理3， 有aixic∈nil(R) ((x-1；σ，δ))，再由文献［10］的命题4得到aixic∈nil(R((x-1；σ，δ))).

一个环R称为NI环，如果nil(R) = Nil*(R)，其中Nil*(R)表示R的上诣零根（R的所有诣零理想的和）。R是NI环当且仅当nil(R)是R的理想当且仅当R/Nil*(R)是约化环。关于NI环的更多性质可见文献［12］。

推论4设R为NI 环且是弱(σ，δ)-相容的环，对左、右零化子有升链条件或R是左（右）Goldie 环，或对理想有升链条件，或R有右Krull维数时，则R是(σ，δ)-SILS右弱McCoy环。

证明 当环R对左、右零化子有升链条件或R是左（右）Goldie 环，或对理想有升链条件，或R有右Krull维数时，nil(R)是幂零理想，则由定理1可得R是(σ，δ)-SILS右弱McCoy环。

设R是一个环，σ是R上的一个自同构，δ是环R的一个σ-导子。我们称环R的一个理想I为σ-理想（σ-不变理想），若σ(I) ⊆I（σ(I) =I）；称I为δ-理想，若δ(I) ⊆I. 若I既是σ-理想（σ-不变理想）又是δ-理想，就称I是一个(σ，δ)-理想（(σ，δ)-不变理想）。

文献［5］给出了q-量子化导子的概念：设δ是环R的一个σ-导子，如果存在q∈R使得qσδ=δσ，就称δ是一个q-量子化σ-导子［5］。

引理4[5］设R是一个环，σ是R上的一个自同构，δ是环R的一个q-量子化σ-导子，其中q是环R的一个中心可逆元且满足σ(q) =q，δ(q) = 0. 如果I是R的一个幂零(σ，δ)-不变理想，则I((x-1；σ，δ))是R((x-1；σ，δ))的一个幂零理想。

命题4设R是一个环，σ是R上的一个自同构，δ是环R的一个q-量子化σ-导子，其中q是环R的一个中心可逆元且满足σ(q) =q，δ(q) = 0. 只要I是R的一个幂零(σ，δ)-不变理想，就有I是(σ，δ)-SILS 右弱McCoy环。

2 (σ，δ)-SILS右弱McCoy的扩张

证明 与命题5类似可证。

推论6设R是一个环，σ是环R上的一个自同构，δ是环R的一个σ-导子，e∈R是一个中心幂等元。如果eR和(1 -e)R都是(σ，δ)-SILS右弱McCoy环，那么R是(σ，δ)-SILS右弱McCoy环。

证明 因为e是R的中心幂等元，由于R=eR⊕(1 -e)R，那么根据推论5，R是(σ，δ)-SILS 右弱Mc-Coy环。

文献［13］介绍了环R[D，C]的相关概念。设D是一个环，C是D的一个子环且包含单位元1，R[D，C]={(d1，d2，…，dn，c，c，…)|di∈D，c∈C，n∈Z+}，则该集合关于分量的加法和乘法构成环。因此若环D上定义了一个自同构σ和σ-导子δ，则可延拓成σˉ，δˉ：R[D，C]→R[D，C]，

推论7设D是一个环，σ是环D上的一个自同构，δ是环D的一个σ-导子，C是D的一个幂零(σ，δ)-不变理想，则D是一个(σ，δ)-SILS右弱McCoy环可推出R[D，C]是一个(σˉ，δˉ)-SILS右弱McCoy环。

上述矩阵有以下包含关系：T(R，n) ⊆Sn(R) ⊆Tn(R). 再用T(R，R)表示环R通过R的平凡扩张，其中加法定义为：(a，b) +(c，d) =(a+c，b+d)，乘法为(a，b)*(c，d) =(ac，ad+bc). 易见，T(R，R)与S2(R)同构。

如果环R上定义了自同构σ和σ-导子δ，那么σ，δ可以延拓到Tn(R)，Sn(R)，T(R，n)或T(R，R)上：σˉ((aij)) =(σ(aij))，δˉ((aij)) =(δ(aij)).

定理2设R是一个环，σ是环R上的一个自同构，δ是环R的一个σ-导子，则S是一个(σˉ，δˉ)-SILS 右弱McCoy环，其中S为Tn(R)，Sn(R)，T(R，n)，T(R，R)中任意一个环。(dij)2= 0，即(dij) ∈nil(Tn(R((x-1；σ，δ)))). 于是有

因而S是(σˉ，δˉ)-SILS右弱McCoy环。

文献［14］介绍了n阶斜上三角矩阵环Tn(R，α). 设R是一个环，α是R的自同态且满足α(1) = 1.Tn(R，α)中元素为上三角矩阵，加法为一般矩阵的加法，乘法满足：Eijr=αj-i(r)Eij，i≤j. 即若A=(aij)，B=(bij) ∈Tn(R，α)，AB=C=(cij)，则cij=aiibij+ai，i+1α(bi+1，j)+ … +aijαj-i(bjj).Tn(R，α) 有 下 列 子 环：S(R，n，α)表示主对角线元素相同的矩阵构成的环，T(R，n，α)表示所有主、次对角线上元素相同的矩阵构成的环，以及

本文中关于(σ，δ)-SILS 右弱McCoy环的结论对(σ，δ)-SILS 左弱McCoy环同样成立，更进一步地，对(σ，δ)-SILS弱McCoy环仍然成立。