有界线性算子及其函数的Browder定理的判定*
2022-10-13仇思楠曹小红
仇思楠,曹小红
陕西师范大学数学与统计学院,陕西 西安 710119
线性算子的谱理论是算子理论的重要组成部分。该理论源于代数方程、线性方程组、积分方程和微分方程的特征值求解问题,与算子方程的求解关系密切。1909 年,Weyl[1]在检测Hilbert 空间上自伴算子所有紧摄动的谱时发现:自伴算子T的所有紧摄动谱集的交集恰好是其谱集中非孤立的有限重特征值全体,这一性质被人们称为Weyl定理。自此之后,一方面,许多学者开始研究哪些算子满足Weyl定理,于是满足Weyl 定理的算子范围不断地扩大[2-9];另一方面,Weyl 定理的形式也在不断变化,其中Weyl 定理的一种变形就是由Harte 和Lee 定义的Browder 定理[10]。近年来,许多学者利用不同的谱集给出了算子满足Weyl 型定理的各种判定方法[11-13]。本文将借鉴文献[11]的思想方法,用一种新定义的谱集来刻画有界线性算子及其函数的Browder定理。
1 预备知识
在本文中,H表示无限维复可分的Hilbert 空间,B(H)表示H上的有界线性算子全体,T*表示T∈B(H)的共轭算子。称算子T∈B(H)为上半Fredholm 算子,若T的零空间N(T)是有限维的且值域

对T∈B(H),算子T的谱,本质谱,Weyl谱,Browder谱,本质逼近点谱,Saphar谱,Kato谱分别表示为σ(T),σe(T),σw(T),σb(T),σea(T),σS(T)以及σK(T). 相应的预解集分别为:ρ(T) = Cσ(T),ρe(T) = Cσe(T),ρw(T) = Cσw(T),ρb(T) = Cσb(T),ρea(T) = Cσea(T),ρS(T) = CσS(T),ρK(T) = CσK(T). 记σC(T) ={λ∈C:R(T-λI)不闭},由Kato 算子定义可知σK(T) =σS(T) ∪σC(T). 此外,记σ0(T) =σ(T)σb(T),ρ+e(T) ={λ∈ρe(T):ind(T-λI) >0}. 用B∘(λ0;ε)表示λ0的ε空心邻域,D 表示单位闭圆盘,Γ 表示单位圆周。对集合E⊆C,用isoE表示E中孤立点的全体,∂E表示E中边界点的全体,accE表示E中聚点的全体,intE表示E中内点的全体。
我们知道,对于T∈B(H),任给多项式p,有σ(p(T)) =p(σ(T)),σe(p(T)) =p(σe(T)),σb(p(T)) =p(σb(T)),σa(p(T)) =p(σa(T)). 特别地,由文献([14,Satz6])知,对于T∈B(H),任给多项式p,有σK(p(T)) =p(σK(T)).
2 有界线性算子的Browder定理
在文献[11]中,作者定义了一个新的谱集σ3(T)并由此研究了有界线性算子T及其函数演算的Weyl型定理。下面将继续该项工作。首先定义集合

令σ3(T) = Cρ3(T),则σ3(T) ⊆σw(T) ⊆σb(T) ⊆σ(T).
设T∈B(H), 算 子T满 足Browder 定 理 是 指σ(T)σw(T) ⊆π00(T) 或σw(T) =σb(T), 其 中π00(T) ={λ∈isoσ(T):0 <n(T-λI) <∞};算 子T满 足Weyl 定 理 是 指σ(T)σw(T) =π00(T). 显 然,Browder 定理只是Weyl 定理的一部分,算子满足Weyl 定理则必定满足Browder 定理,反之,若算子满足Browder定理,则未必满足Weyl定理。
下面,借助σ3(T)来刻画有界线性算子及其函数的Browder定理。
定理1设T∈B(H),则下列叙述等价:
(i)T满足Browder定理;
(ii)σ(T) =σ3(T) ⋃isoσ(T);
(iii)accσ(T) ⊆σ3(T);
(iv)σ3(T) = accσ(T) ⋃{λ∈C:n(T-λI) = ∞};
(v)intσ(T) ⊆σ3(T);
(vi)σ(T) =σ3(T) ⋃∂σ(T);
(vii)intσ(T) = intσ3(T);
(viii)accσ(T) = accσ3(T) ⋃accisoσ(T);
(ix)σ3(T) = intσ(T) ⋃{λ∈C:n(T-λI) = ∞}⋃[accσ(T) ⋂∂σ(T)];
(x)σ(T) = accσ3(T) ⋃{λ∈C:n(T-λI) = ∞}⋃σC(T) ⋃σ0(T);
(xi)σ(T) = accσ3(T) ⋃{λ∈C:n(T-λI) = ∞}⋃σK(T);
(xii)σ(T) =σ3(T) ⋃σC(T) ⋃σ0(T);
(xiii)σ(T) =σ3(T) ⋃σK(T).
证明
(i)⇒(ii)任 给λ0∉σ3(T) ⋃isoσ(T),由ρ3(T) 的 定 义 及 已 知 条 件T满 足Browder 定 理 可 知λ0∈ρ(T) ⋃isoσ(T). 又由于λ0∉isoσ(T),因此λ0∉σ(T).反包含显然成立。
(ii)⇒(iii)由accσ(T) ⊆σ(T) =σ3(T) ⋃isoσ(T)知accσ(T) ⊆σ3(T).
(iii)⇒(iv)对任意λ0∉accσ(T) ⋃{λ∈C:n(T-λI) = ∞},则λ0∈ρ(T) ⋃isoσ(T),且n(T-λ0I) <∞,于是λ0∉σ3(T).反包含显然成立。
(iv)⇒(v)显然。
(v)⇒(vi)σ(T) = intσ(T) ⋃∂σ(T) ⊆σ3(T) ⋃∂σ(T).
(vi)⇒(vii)由intσ(T) ⊆σ(T) =σ3(T) ⋃∂σ(T)知intσ(T) ⊆σ3(T),于是intσ(T) ⊆intσ3(T). 反包含显然成立。
(vii)⇒(i)设T-λ0I是Weyl 算子,则λ0∉intσ3(T) = intσ(T),所以λ0∈ρ(T) ⋃∂σ(T),故T-λ0I是Browder算子。
(ii)⇒(viii)显然。
(viii)⇒(i)设T-λ0I是Weyl 算子,则λ0∉accσ3(T) ⋃accisoσ(T),因此λ0∉accσ(T),于是T-λ0I是Browder算子。
(iii) ⇒ (ix) 对 任 意λ0∉intσ(T) ∪{λ∈C:n(T-λI) = ∞}⋃[accσ(T) ⋂∂σ(T)], 则λ0∈ρ(T)⋃isoσ(T),且n(T-λ0I)<∞,因此λ0∉σ3(T). 反包含显然成立。
(ix)⇒(v)显然。
(i)⇒(x)任给λ0∉accσ3(T) ⋃{λ∈C:n(T-λI) = ∞}⋃σC(T) ⋃σ0(T),则T-λ0I是上半Fredholm算子且λ0∈ρ3(T) ⋃isoσ3(T)且λ0∉σ0(T). 由半Fredholm 算子的摄动理论以及ρ3(T)的定义知T-λ0I为Weyl算子。由于T满足Browder定理,则T-λ0I为Browder算子,又由于λ0∉σ0(T),于是λ0∉σ(T). 反包含显然成立。
(x)⇒(xi)显然。
(xi)⇒(i)设T-λ0I是Weyl 算子,则存在ε>0,当0 <|λ-λ0|<ε时,λ∈ρw(T) ⋂ρK(T). 所以λ∉accσ3(T) ⋃{λ∈C:n(T-λI) = ∞}⋃σK(T),从而T-λI可逆。于是T-λ0I是Browder算子。

(xii)⇒(xiii)显然。
(xiii)⇒(i)设T-λ0I是Weyl 算子,则存在ε>0,当0 <|λ-λ0|<ε时,λ∈ρw(T) ⋂ρK(T). 所以λ∉σ3(T) ⋃σK(T),从而T-λI可逆。于是T-λ0I是Browder算子。
注1
(i)当T满足Browder定理时,定理1的(x)中σ(T)分解的四部分缺一不可。
例2令T∈B(ℓ2)定 义 为:T(x1,x2,x3,…) =(0,x1,x2,x3,…),则σ(T) =σw(T) =σb(T) = D,但 是{λ∈C:n(T-λI) = ∞}=σ0(T) = ∅,σC(T) = Γ,σ(T) ≠{λ∈C:n(T-λI) = ∞}⋃σC(T) ⋃σ0(T), 故accσ3(T)不能缺。
例3令T∈B(ℓ2)定义为:T(x1,x2,x3,…) =(0,x2,x3,x4,…),则σ(T) ={0,1},σw(T) =σb(T) ={1},即T满 足Browder 定 理。 但 是accσ3(T) =σC(T) = ∅,{λ∈C:n(T-λI) = ∞}={1},σ0(T) ={0},σ(T) ≠accσ3(T) ⋃σC(T) ∪σ0(T),故{λ∈C:n(T-λI) = ∞}不能缺。σ(T) ≠accσ3(T) ⋃{λ∈C:n(T-λI) = ∞}⋃σC(T),故σ0(T)不能缺。

(iv)σ(T) =σ3(T)当且仅当T满足Browder定理且{λ∈isoσ(T):n(T-λI) <∞}= ∅.
证 明 必 要 性。根 据 定 理1,T满 足Browder 定 理 显 然 成 立。由{λ∈isoσ(T):n(T-λI) <∞}⊆ρ3(T) =ρ(T)知{λ∈isoσ(T):n(T-λI) <∞}= ∅.
充分性。σ(T) ⊇σ3(T) 显然。下证σ3(T) ⊇σ(T). 若λ0∉σ3(T),由T满足Browder 定理,则λ0∈ρ(T) ⋃isoσ(T),但是{λ∈isoσ(T):n(T-λI) <∞}= ∅,于是λ0∉σ(T).
(v)当accσ(T) = accσ3(T)时,T满足Browder 定理。反之不成立。如例4,虽然T满足Browder 定理,但是accσ(T) ={0},accσ3(T) = ∅,accσ(T) ≠accσ3(T).
(vi)accσ(T) = accσ3(T)当且仅当T满足Browder定理且E= ∅,其中
E={λ∈C:存在ε>0,当0 <|μ-λ|<ε时,n(T-μI) <∞,并且μ∈ρ(T) ⋃isoσ(T)}⋂accisoσ(T).
证明 必要性。当accσ(T) = accσ3(T)时,E⊆accσ(T),但E∩accσ3(T) = ∅,故E= ∅.
充分性。任给λ0∉accσ3(T),则由T满足Browder 定理可知存在ε>0,使得当0 <|μ-λ0|<ε时,n(T-μI) <∞并且μ∈ρ(T) ⋃isoσ(T). 由E= ∅ 知,λ0∉accisoσ(T). 从 而 当0 <|μ-λ0|<ε时,μ∈ρ(T),即λ0∈ρ(T) ⋃isoσ(T). 故accσ(T) = accσ3(T).
在定理1 中,主要用σ(T)与σ3(T),accσ(T)与σ3(T),intσ(T)与σ3(T),σ(T)与accσ3(T)之间的关系来刻画算子T的Browder 定理。接下来,继续用σ(T)与accσ3(T)之间的关系来讨论算子T的Browder定理。
推论1设T∈B(H),则下列叙述等价:
(i)T满足Browder定理;

证明
(i)⇒(ii) 任 给λ0∉accσ3(T) ⋃accisoσ(T) ⋃{λ∈C:n(T-λI) = ∞}⋃{λ∈isoσ(T):n(T-λI) <d(T-λI)}⋃σ0(T),由定理1 可知,λ0∈ρ(T) ⋃isoσ(T). 断言:λ0∉isoσ(T). 若否,则n(T-λ0I) ≥d(T-λ0I),又n(T-λ0I) <∞,从而T-λ0I是Fredholm算子。由于λ0∈isoσ(T),因此λ0∈σ0(T). 这与λ0∉σ0(T)矛盾。于是λ0∉σ(T)得证。反包含显然成立。
(ii)⇒(iii)显然。
(iii)⇒(i)设T-λ0I是Weyl 算子,则存在ε>0,使得当0 <|μ-λ0|<ε时,μ∈ρw(T) ⋂ρS(T). 故μ∉accσ3(T) ⋃accisoσ(T) ⋃{λ∈C:n(T-λI) = ∞}⋃{λ∈isoσ(T):n(T-λI) <d(T-λI)}⋃σS(T),从而μ∉σ(T). 于是λ0∈ρ(T) ⋃isoσ(T),即T-λ0I是Browder算子。
接下来,用σ(T)和intσ3(T)之间的关系来讨论算子T的Browder定理。推论2设T∈B(H),则下列叙述等价:
(i)T满足Browder定理;
(ii)σ(T) = intσ3(T) ⋃{λ∈∂σ(T):n(T-λI) <d(T-λI)}⋃{λ∈C:n(T-λI) = ∞}⋃σ0(T);
(iii)σ(T) = intσ3(T) ⋃{λ∈∂σ(T):n(T-λI) <d(T-λI)}⋃{λ∈C:n(T-λI) = ∞}⋃σS(T).
证明
(i)⇒(ii)任给λ0∉intσ3(T) ⋃{λ∈∂σ(T):n(T-λI) <d(T-λI)}⋃{λ∈C:n(T-λI) = ∞}⋃σ0(T),则 对 任 意Bo(λ0,ε), 存 在λ1∈Bo(λ0,ε), 使 得λ1∈ρ3(T). 于 是 存 在λ2∈Bo(λ0,ε), 使 得λ2∈ρw(T) ∪ρS(T). 由T满足Browder 定理,所以λ2∈ρ(T). 因此λ0∈ρ(T) ⋃∂σ(T). 若λ0∈∂σ(T),则T-λ0I是Fredholm 算子,由Fredholm 算子的摄动定理可知,T-λ0I是Weyl算子,又由T满足Browder定理且λ0∉σ0(T) 得到λ0∈ρ(T). 反包含显然成立。
(ii)⇒(iii)显然。
(iii)⇒(i)设T-λ0I是Weyl 算子,则存在ε>0,使得当0 <|μ-λ0|<ε时,μ∈ρw(T) ⋂ρS(T). 故μ∉intσ3(T) ⋃{λ∈∂σ(T):n(T-λI) <d(T-λI)}⋃{λ∈C:n(T-λI) = ∞}⋃σS(T), 从 而μ∉σ(T).于是λ0∈ρ(T) ⋃isoσ(T),因此T-λ0I是Browder算子。
注2
(i)在推论1和推论2中,通过举例可知,当T满足Browder定理时,σ(T)分解的几部分仍然是缺一不可的。
(ii)intσ3(T) = ∅且T满足Browder定理当且仅当
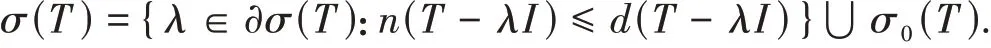
证明 必要性。由条件及推论2 知σ(T) ={λ∈∂σ(T):n(T-λI) <d(T-λI)}⋃{λ∈C:n(T-λI) =∞}⋃σ0(T). 容易证明

于是可得
所以σ(T) ={λ∈∂σ(T):n(T-λI) ≤d(T-λI)}∪σ0(T).
充分性。因为σ(T) ={λ∈∂σ(T):n(T-λI) ≤d(T-λI)}⋃σ0(T) ⊆∂σ(T),所以intσ(T) = ∅,于是intσ3(T) = ∅,根据定理1可知T满足Browder定理。
(iii)由前面的结论,当σ(T) =σ3(T) 或accσ(T) = accσ3(T) 或intσ(T) = intσ3(T) 时,T均 满 足Browder定理。但是,当∂σ(T) = ∂σ3(T)时,无法确定T是否满足Browder定理。下面,举例进行说明。
例5设A,B∈B(ℓ2)分别定义为:A(x1,x2,x3,…) =(0,x1,x2,x3,…),B(x1,x2,x3,…) =(x2,x3,x4,…),令T= diag(A,B),则σ(T) = D,σ3(T) = Γ,∂σ(T) = ∂σ3(T),但是σb(T) = D,σw(T) = Γ,故T不满足Browder定理。

(i)T满足Browder定理;
(ii)σ3(T) = intσ(T) ⋃∂σ3(T);
(iii)σ(T) = ∂σ3(T) ⋃isoσ(T) ⋃accσw(T);
(iv)σ(T) = ∂σ3(T) ⋃{λ∈C:n(T-λI) <d(T-λI)}⋃accσw(T) ⋃σ0(T);
(v)σ(T) = ∂σ3(T) ⋃{λ∈C:n(T-λI) <d(T-λI)}⋃accσw(T) ⋃σS(T).
证明
(i)⇒(ii)因为T满足Browder定理,根据定理1,故σ3(T) = intσ(T) ⋃∂σ3(T).
(ii) ⇒(iii)σ(T) =σ3(T) ⋃[ρ3(T) ⋂σ(T)]= intσ(T) ⋃∂σ3(T) ⋃[ρ3(T) ⋂σ(T)]. 由σ3(T) =intσ(T) ⋃∂σ3(T) 知,ρw(T) ⊆ρ(T) ⋃∂σ(T). 故T满 足Browder 定 理,于 是intσ(T) ⊆accσw(T),ρ3(T) ⋂σ(T) ⊆isoσ(T). 因此∂σ3(T) ⋃isoσ(T) ⋃accσw(T) ⊇σ(T). 反包含显然成立。
(iii)⇒(iv)由(iii)知σ(T) = ∂σ3(T) ⋃isoσ(T) ⋃accσw(T),又因为

所以σ(T) ⊆∂σ3(T) ∪{λ∈C:n(T-λI) <d(T-λI)}⋃accσw(T) ⋃σ0(T). 反包含显然成立。
(iv)⇒(v)显然。
(v)⇒(i)设T-λ0I是Weyl 算子,则存在ε>0,使是当0 <|μ-λ0|<ε时,μ∈ρw(T) ⋂ρS(T). 故μ∉∂σ3(T) ⋃{λ∈C:n(T-λI) <d(T-λI)}⋃accσw(T) ⋃σS(T), 从 而μ∉σ(T). 于 是λ0∈ρ(T) ⋃isoσ(T),因此T-λ0I是Browder算子。
注3
(i)设T满足Browder定理且{λ∈isoσ(T):n(T-λI) <∞}= ∅,则∂σ(T) = ∂σ3(T). 反之不成立。
事实上,由T满足Browder 定理知ρ3(T) ={λ∈isoσ(T):n(T-λI) <∞}⋃ρ(T) =ρ(T),于是∂σ(T) =∂σ3(T). 而当∂σ(T) = ∂σ3(T)时,一定有{λ∈isoσ(T):n(T-λI) <∞}= ∅.
(ii)T满足Browder定理且{λ∈isoσ(T):n(T-λI) <∞}= ∅当且仅当σ(T) =σ3(T).
(iii)T满足Browder定理且∂σ(T) = ∂σ3(T)当且仅当σ(T) =σ3(T).
3 算子函数的Browder定理
我们知道,算子满足Browder 定理并不能推出其函数演算满足Browder 定理。接下来,借助σ(T)和σ3(T)之间的关系来讨论算子函数的Browder定理。
定理2设T∈B(H),则对任意的多项式p,p(T)满足Browder定理当且仅当
(i)T满足Browder定理;
(ii) 对任意多项式p,p(σ3(T)) ⊆σw(p(T)).
证明 必要性。(i)显然成立。对任意多项式p,p(σ3(T)) ⊆p(σb(T)) =σb(p(T)) =σw(p(T)),故(ii)成立。
充分性。先证明对任意λ,μ∈ρe(T),有ind(T-λI) · ind(T-μI) ≥0. 反证:若存在λ0,μ0∈ρe(T),使得ind(T-λ0I) =n>0,ind(T-μ0I) = -m<0,其中n和m都是正整数。令p0(T) =(T-λ0I)m(T-μ0I)n,则p0(T)为Weyl算子,而0 =p0(λ0)=p0(μ0) ∈p0(σ3(T)) ⊆σw(p0(T)),矛盾。故对任意λ,μ∈ρe(T),有ind(T-λI) · ind(T-μI) ≥0. 设p(T) -μI是 Weyl 算 子, 令p(x) -μ=a(x-λ)n1(x-λ)n2…(x-12λk)nk,μ=p(λi),i= 1,…,k.则p(T) -μI=a(T-λ1I)n1(T-λ2I)n2…(T-λkI)nk,且

所以T-λiI是Weyl算子。故T-λiI是Browder算子,于是p(T) -μI是Browder算子。
注4对于定理2,考虑这样一个问题:条件“对任意多项式p,p(σ3(T)) ⊆σw(p(T))”在什么情况下可以加强为“对任意多项式p,p(σ3(T)) =σw(p(T))”?为此,有如下结论。
设T∈B(H),则对任意的多项式p,p(T)满足Browder 定理且{λ∈isoσ(T):n(T-λI) <∞}=σ0(T)当且仅当
(i)T满足Browder定理;
(ii)对任意多项式p,p(σ3(T)) =σw(p(T)).
证明 必要性。只需证p(σ3(T)) ⊇σw(p(T)). 对任意μ0∉p(σ3(T)),令p(x) -μ0=a(x-λ1)n1(x-λ2)n2…(x-λk)nk,μ0=p(λi),i= 1,…,k. 则p(T) -μ0I=a(T-λ1I)n1(T-λ2I)n2…(T-λkI)nk. 显 然λi∉σ3(T). 从而λi∈ρ(T) ⋃isoσ(T). 不妨设λi∈isoσ(T),则由已知条件得λi∈σ0(T),因此T-λiI是Browder算子。故μ0∉σw(p(T)).
充分性。只需证{λ∈isoσ(T):n(T-λI) <∞}⊆σ0(T). 由已知条件可知σ3(T) =σw(T),又因为{λ∈isoσ(T):n(T-λI) <∞}⊆ρ3(T),所以{λ∈isoσ(T):n(T-λI) <∞}⊆σ0(T).
推论4设T∈B(H),则对任意的多项式p,p(T)满足Browder定理当且仅当
(i)T满足Browder定理;
(ii)对任意多项式p,p(σ3(T) ⋂ρe(T)) ⋂ρw(p(T)) = ∅.
证明 必要性。由定理2 知,对任意多项式p,p(σ3(T) ⋂ρe(T)) ⊆p(σ3(T)) ⊆σw(p(T)). 因此p(σ3(T) ⋂ρe(T)) ⋂ρw(p(T)) = ∅.
充分性。根据定理2,只需证对任意多项式p,p(σ3(T)) ⊆σw(p(T)). 对任意μ0∉σw(p(T)),设p(T) -μ0I=a(T-λ1I)n1(T-λ2I)n2…(T-λkI)nk,则T-λiI是Fredholm 算子,其中i= 1,…,k.若存在j,使得ind(T-λjI) >0,则λj∈σ3(T),从而p(σ3(T) ⋂ρe(T)) ⋂ρw(p(T)) ≠∅,矛盾。于是任意1 ≤i≤k有ind(T-λiI) ≤0. 同理可得任意1 ≤i≤k有ind(T-λiI) ≥0. 从而λi∉σ3(T),故μ0∉p(σ3(T)).
推论5设T∈B(H),则对任意的多项式p,p(T)满足Browder定理当且仅当
(i)T满足Browder定理;
(ii)对任意多项式p,p(σ3(T)) =σ3(p(T)).
证明 充分性。由定理2,显然。

下证σ3(p(T)) ⊆p(σ3(T)). 任意μ0∉p(σ3(T)),设p(T) -μ0I=a(T-λ1I)n1(T-λ2I)n2…(T-λkI)nk,其中i= 1,…,k. 则λi∉σ3(T),从而n(p(T) -μ0I) <∞. 由T满足Browder 定理,λi∈ρ(T) ⋃isoσ(T). 不妨设λi∈isoσ(T),i= 1,…,k. 则{λi},i= 1,…,k,为k个开闭集,从而T= diag(T1,T2,…,Tk,A),其中σ(Ti)={λi},σ(A) =σ(T){λ1,…λk}. 于 是p(T) = diag(p(T1),p(T2),…,p(Tk),p(A)), 其 中σ(p(Ti)) =p(σ(Ti)) ={μ0},σ(p(A)) =p(σ(A)). 因 为λi∉σ(A),故μ0∉p(σ(A)),于 是μ0∈isoσ(p(T)),因 此μ0∉σ3(p(T)).
定理3设T∈B(H),则对任意的多项式p,p(T)满足Browder定理当且仅当T满足Browder定理且下列之一成立:
(i)ρ+e(T) = ∅;
(ii)σ3(T) ⊆σe(T) ⋃σea(T).
证明 必要性。T满足Browder定理显然成立。下面证明(i),(ii)至少有一个成立。采用反证法,若存在λ1∈ρ+e(T)且λ2∈σ3(T) ⋂ρe(T) ⋂ρea(T),则T-λ1I是Fredholm 算子且ind(T-λ1I) =n>0,T-λ2I是Fredholm 算子且ind(T-λ2I) = -m<0,其中n和m都是正整数。令p(T) =(T-λ1I)m(T-λ2I)n,则p(T)为Fredholm 算子且ind(p(T)) = 0,由p(T)满足Browder 定理,从而p(T)是Browder 算子,因此T-λ1I是Browder 算子,这与ind(T-λ1I) >0 矛盾。故ρ+e(T) = ∅与σ3(T) ⊆σe(T) ⋃σea(T)至少有一个成立。
充分性。若(i)成立,即若T-λI是Fredholm 算子,则ind(T-λI) ≤0. 设p(T) -μ0I是Weyl算子,令p(x) -μ0=a(x-λ1)n1(x-λ2)n2…(x-λk)nk,μ0=p(λi),i= 1,…,k. 则p(T) -μ0I=a(T-λ1I)n1(T-λ2I)n2…(T-λkI)nk且0 = ind(p(T) -μ0I) =n1ind(T-λ1I) +n2ind(T-λ2I) + … +nkind(T-λkI), 所 以T-λiI是Weyl算子,又T满足Browder定理,故T-λiI是Browder算子,于是p(T) -μ0I是Browder算子。
同理,若(ii)成立,由ρ3(T)的定义及Fredholm 算子的摄动定理可知,若T-λI是Fredholm 算子,则ind(T-λI) ≥0. 于是,仍可证得对任意的多项式p,p(T)满足Browder定理。
事实上,σ3(T) ⊆σe(T) ⋃σea(T*)当且仅当ρ+e(T) = ∅. 因此,有如下推论。
推论6设T∈B(H),则对任意的多项式p,p(T)满足Browder定理当且仅当T满足Browder定理且下列之一成立
(i)σ3(T) ⊆σe(T) ⋃σea(T*);
(ii)σ3(T) ⊆σe(T) ⋃σea(T).
