无人机高机动抗扰轨迹跟踪控制方法
2022-10-13王英勋宋欣屿赵江蔡志浩
王英勋 宋欣屿 赵江 蔡志浩
(北京航空航天大学 自动化科学与电气工程学院, 北京 100083)
近年来,四旋翼无人机以其独特的外形、结构与飞行方式逐渐成为国内外关注的热点。 与常规布局的直升机相比,四旋翼无人机机械结构简单,成本较低,易于维护,4 个螺旋桨对称分布,使得四旋翼无人机的机动能力更强,静态盘旋的稳定性更好,也更容易实现机型的微小型化。 四旋翼无人机特别适合在近地面环境(如室内、城市和丛林等)中执行监视、侦察等任务,具有广阔的应用前景[1]。 在进行这些任务时,往往需要无人机进行高速度、高加速度、高角速度、高角加速度的运动,然而,四旋翼在高机动飞行时,系统呈现严重的非线性和非定常特性,气动阻力难以建模,给控制器设计带来了很大的难度。 此外,精准的跟踪高机动轨迹还需要参考其高阶时间导数,即加加速度和加加加速度。 传统的控制方法难以解决建模不准和扰动的问题,也无法考虑轨迹的高阶时间导数,在高机动飞行时控制效果不佳,难以跟踪机动性较强的轨迹[2]。
非线性动态逆控制(nonlinear dynamic inversion, NDI)通过对动态系统求逆来实现非线性控制系统反馈线性化,是非线性控制中的一种较为有效的方法[3],在飞行器控制领域被广泛应用[4],对非线性控制系统具有很好的跟踪性能。但是NDI 对建模误差十分敏感,控制器的鲁棒性较低[5]。 针对这一问题,Sieberling 等[6]在NDI 基础上提出了增量非线性动态逆控制(incremental nonlinear dynamic inversion, INDI),通过角加速度反馈解决了NDI 鲁棒性不足的问题,实现了对固定翼无人机姿态的控制,但只进行了仿真,未进行试飞测试。 Simplício 等[7]将INDI 用于 直 升 机 悬停控制,验证了INDI 对模型的依赖性较低,具有较强的鲁棒性,但不适用于轨迹跟踪控制。 Lu等[8]用INDI 实现了固定翼有人机作动器故障时的轨迹跟踪控制。 近年来,INDI 逐渐被用于四旋翼无人机的控制领域[9-14],但在估计角加速度时,均采用了延迟较大的方法,对控制精度有着较大的影响。
角加速度不易测量[11,15],角加速度计是测量飞行器角加速度最直接的装置,但由于成本和飞行器尺寸的限制,还未应用于小型无人机[16-18]。虽然也可以通过线加速度计间接测量角加速度值,但需要在机身上合理布置至少3 组加速度计,难以实现[19-21]。 除却测量角加速度外,国内外也提出了多种数值估计方法用以计算角加速度的估计值。 最常见的方法是对角速度进行微分获取角加速度的估计值,但其会放大噪声的影响,为此引入低通滤波器,但又会带来一定的延迟。 为了在不引入延迟的同时抑制噪声,Valiviita 和Ovaska[22]提出了一种预测低通滤波器,虽然取得了很好的效果,但其假设加速度可以通过分段低次多项式准确近似,不适用于机动性较强的无人机。Smeur 等[9]使用低通滤波同时处理角加速度和控制输入,实现了滞后同步,虽然看起来很简单,但滞后时间是不确定的。 此外,卡尔曼滤波器基于以高斯白噪声为输入的恒定加速度模型[23-25],但实际上无人机的飞行并不一定表现出类似的稳定随机过程[26-27]。
本文主要创新点如下:①设计了基于INDI 方法的轨迹跟踪控制器,为减小轨迹跟踪的延迟,引入了微分平坦前馈。 ②由于角加速度无法直接获得,INDI 方法对其又非常敏感,本文设计了多种角加速度估计方法,并通过飞行试验选择了效果最佳的估计方法。 ③通过飞行试验验证了所提控制器具有高精度的高机动轨迹跟踪效果,且具有较强的抗扰能力。
1 预备知识
1.1 无人机模型
本文研究对象为小型四旋翼无人机,惯性参考坐标系选择北东地坐标系,其正交基为(ix,iy,iz),机体坐标系固定在四旋翼飞行器上,坐标原点与其质心重合,如图1 所示。
图1 中所示的单位矢量是机体坐标系下的基向量,形成从机体坐标系到惯性参考坐标系的转换旋转矩阵R=(bxbybz)∈SO(3),即
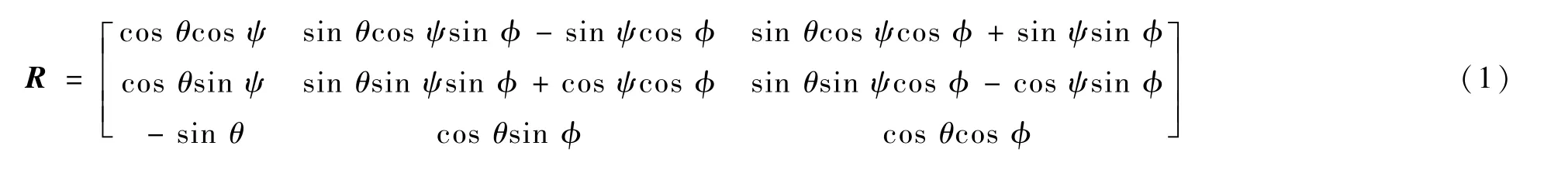

图1 四旋翼及机体坐标系定义Fig.1 Quadrotor with body-fixed reference system
四旋翼无人机的质心运动模型为

式中:x和v分别为惯性参考坐标系下的位置和速度。 加速度主要考虑3 项:①向下的重力加速度g;②推重比τ为总推力T和机体质量m之比,由于推力矢量沿机体坐标系的bz的反方向,四旋翼向前、向后或侧向加速时必须进行俯仰或滚转运动;③外部干扰力矢量fext,其包含所有作用于机体的其他力(如空气阻力)。

假定每个螺旋桨轴均与bz轴完美平行,用Ti和Qi来描述每个电机产生的推力和扭矩,则有
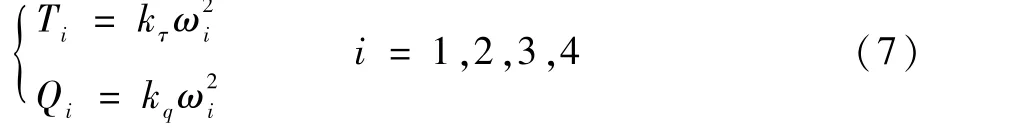
式中:ωi>0(i=1,2,3,4)为每个电机的旋转速度;kτ为电机推力系数;kq为电机扭矩系数。
电机的序号和旋转方向如图2 所示。
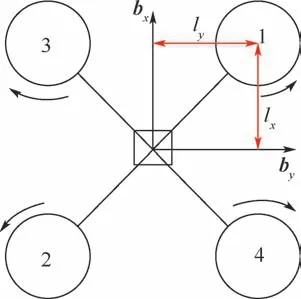
图2 旋翼序号及旋转方向Fig.2 Rotor serial number and rotation direction

1.2 微分平坦前馈
控制器的目标是精准地跟踪由式(12)定义的参考轨迹:
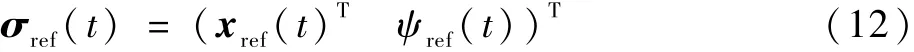
σref(t)由4 个微分平坦输出组成,即惯性参考坐标系下的四旋翼位置xref(t) ∈R3和机身偏航角ψref(t)∈T,T 表示圆组。
假设xref的前四阶导数存在且连续,ψref前二阶导数存在且连续。 在惯性参考坐标系中,xref对时间求导依次产生参考速度vref、参考加速度aref、参考加加速度jref和参考加加加速度sref,即


通过上面的推导,可以将轨迹跟踪问题重新构造为状态跟踪问题,将推导出的参考角速度Ωref和参考角加速度Ω·ref关于参考轨迹加加加速度sref、加加速度jref、偏航角速度̇ψref和偏航角加速度¨ψref的表达式,作为轨迹跟踪控制中的前馈输入。
1.3 增量非线性动态逆控制原理
常规非线性系统的状态空间表达式可以写为
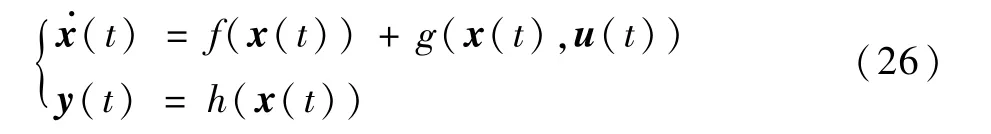
式中:x(t)为状态向量;u(t)为控制输入向量;y(t)为输出向量。 不同于NDI 方法将整个系统的动态特性求逆,INDI 方法在当前时刻的状态x0和控制输入u0下对系统的动态特性进行线性化并求逆。
使用一阶泰勒级数展开式重写式(26),忽略其他高阶项可得

2 基于前馈INDI 的抗扰控制器设计
总体控制框架如图3 所示。 其中,无人机的加速度由加速度计测得,用ab表示在机体坐标系下未经过滤波的加速度测量值,用a表示惯性参考坐标系下经过重力加速度校正的加速度,则有
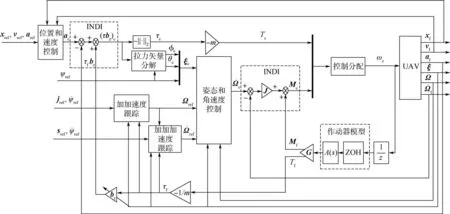
图3 总体控制框图Fig.3 Overall control diagram

无人机的位置信息由OptiTrack 提供,为了融合加速度计和OptiTrack 的信息,采用了扩展卡尔曼滤波(EKF)方法,获得了经过EKF 处理后的位置xf、速度vf、加速度af。 角速度由陀螺仪测量得到,根据角速度信息和角加速度估计方法得到角加速度的估计值Ω·f。
2.1 位置和速度控制
位置和速度控制基于2 个串联的PD 控制器,所得的控制器表达式为

式中:Kx为位置环对角增益矩阵;Kv为速度环对角增益矩阵;下标ref 表示从参考轨迹获得的参考值,下标c 表示控制器计算的命令值。 式中的前2 项确保跟踪参考位置和参考速度,最后1 项作为前馈输入以确保跟踪参考加速度,得到的加速度命令用于计算推力和姿态命令。
位置和速度控制原理框图如图4 所示。
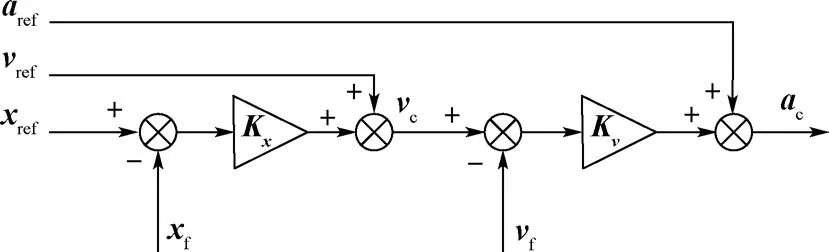
图4 位置和速度控制Fig.4 Position and velocity control
2.2 INDI 加速度控制

加速度控制原理框图见图3 左侧虚线部分。
2.3 姿态和角速度控制
式(36)和已知的偏航角参考值ψref共同构成姿态角指令:

式中:τf为根据电机转速估计值和推力模型估算的当前推重比。
式(34)增量性质使控制器可以在存在干扰或建模误差的情况下实现对加速度的控制,所需的推重比为


姿态和角速度控制的原理框图如图5 所示。
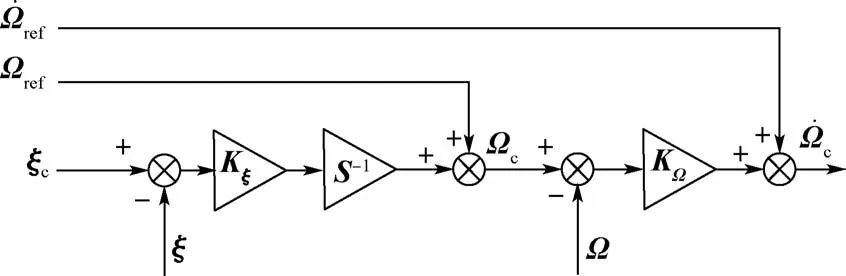
图5 姿态和角速度控制Fig.5 Attitude and angular rate control
2.4 INDI 角加速度控制
由式(5)可知
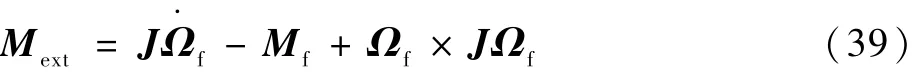
式中:Mf为机体坐标系下根据转速指令计算的控制力矩。
将式(39)代入式(5)可得
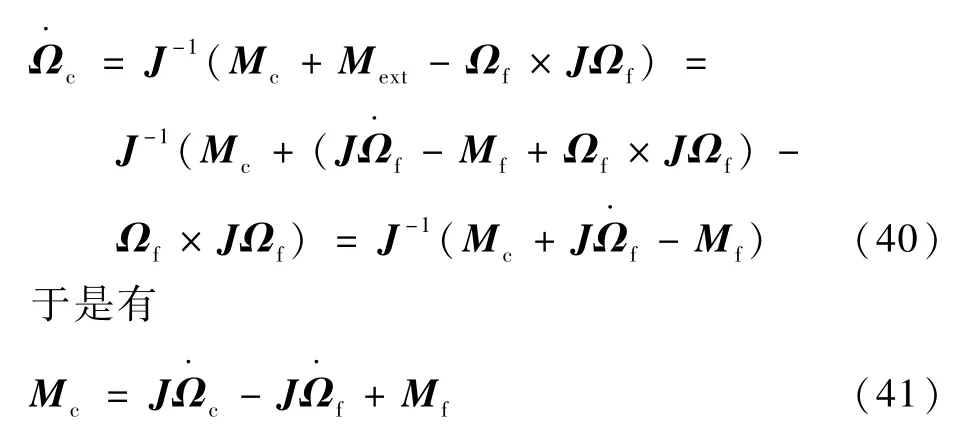
由于角加速度无法直接获得,需要通过角加速度估计方法进行估算,Ω·f有一定时间延迟,式(41)中所有变量应为同一时刻,否则该式是错误的,造成系统振荡发散。 因此,在利用当前时刻电机转速估算控制力矩Mf时,应使其延迟与角加速度估计延迟保持一致。 角加速度控制原理框图见图3 中间虚线部分。
2.5 电机转速估计
由于缺少电机转速的传感器和电调的转速反馈,引入作动器模型以获得当前时刻的电机转速的估计值。 电机转速指令与其响应之间的动态关系可以表示为连续的一阶传递函数。
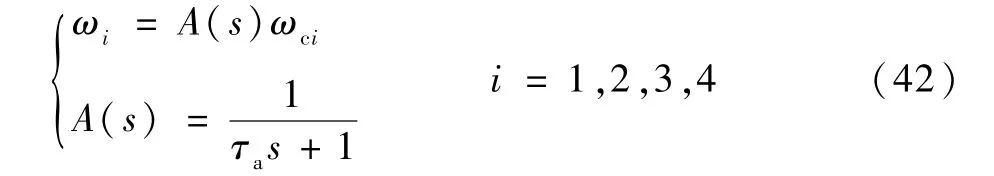
式中:ωci(i=1,2,3,4)为每个电机的转速指令;τa为可以通过参数辨识获得的作动器时间常数。
根据估计的转速和1.1 节中的无人机模型,即可估算无人机当前时刻的推重比τf和控制力矩Mf。
2.6 基于互补滤波的低延迟角加速度估计
INDI 基于加速度反馈,降低了对模型气动参数的敏感性,提高了控制的鲁棒性,因此,加速度值的准确性和实时性是实现上述方法的基础。 在实际应用中,小型无人机由于体积和成本的原因,主要装备的是惯性传感器(inertial measurement unit,IMU),无法直接获得角加速度,因此需要设计延迟低、精度高的方法对角加速度进行估计。
2.6.1 基于模型预测法的角加速度估计
根据飞行器的动力学方程(5),可以通过理论估计方法计算出角加速度信号,如下:


由于实际中无法对飞行器的参数和空气动力学准确建模,控制力矩会受到模型不确定性的影响,无法准确估计,此外系统扰动无法准确建模,模型预测方法无法考虑实际飞行中外界干扰的影响,外界干扰的影响会导致估计结果偏离真值。虽然该方法的鲁棒性较差,在实际中不能很好地估计角加速度,但其不使用微分运算,也不需要低通滤波器,因此噪声很小,相位滞后几乎为零。 由于模型预测方法是一种基于系统非线性动力学方程的理论估计方法,其动态响应非常快。
2.6.2 基于微分法和低通滤波的角加速度估计
微分法是现实中估计角加速度信号最直接和最常用的方法。 由于微分运算对系统噪声有严重的放大作用,会导致信号性能变差,通常使用二阶巴特沃斯低通滤波器(low-pass filter, LPF) 对IMU 信号进行滤波,以减轻机身振动和其他噪声的影响,再进行微分运算获取角加速度。
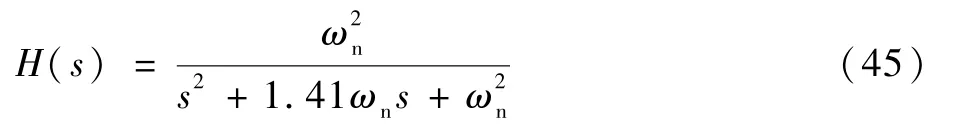
式中:ωn为低通滤波器的截止频率。
很难找到一种低通滤波器,既能表现出小的相位滞后,又能抑制微分操作引起的放大噪声。但该方法不依赖于系统模型参数,其估计结果可以有效地反映外界干扰和系统不确定性的影响,从而能够真实地估计出实际角加速度信号的变化。
2.6.3 基于互补滤波的角加速度估计
模型预测方法具有噪声少、相位滞后小的优点,可以弥补微分法的不足。 微分法可以估计实际角加速度信号的真值,弥补模型预测估计结果的误差。 因此,基于互补滤波(complementary filter, CF)理论的思想对估计结果进行数据融合,可以得到较好的估计结果。

通过推导,角加速度的最终估计值如下:

图6 互补滤波Fig.6 Complementary filter

从方程(48)可以看出,T(s)为一个高通滤波器,其保留了模型预测方法的有益的高通特性,并抑制影响低频不确定性和干扰;S(s)为一个低通滤波 器,可 滤除Ω·^D(s)的高频噪声并保留信号的低通特性。 由于G(s)是一个积分器,G(s)Ω·^D(s)
是可以通过IMU 测量的角速度信号。 因此,IMU的测量值可以直接用于数据融合方法的实际实现中,巧妙地避免了整个估计过程中的微分运算。因此,该方法不会遇到由差分操作引起的噪声放大问题。
T(s) +S(s) =1 是互补性的体现。 它将每种方法的有利部分保留在最终估计结果中,并确保截止频率彼此相同。 因此,微分法的相位滞后问题通过补偿模型预测方法的高通特性来解决。 通过角速度信号的反馈,可以消除外界干扰和模型不确定性的影响。 综上所述,该估计方法的最大优点是在估计过程中巧妙避免了微分运算,有效降低噪声的放大效应,提高信号性能。
采集实飞数据,分别用较为常用的直接微分法、卡尔曼滤波方法和互补滤波方法进行角加速度估计。 直接微分法由于噪声被放大,根据多次试验,选择了延迟相对较小且对噪声抑制效果较好的、截止频率为70 rad/s 的二阶巴特沃斯低通滤波器滤波处理。 卡尔曼滤波器中由于控制器的控制周期为250 Hz,因此ΔT=0.004 s。 互补滤波器的H(s)根据试验反复调整到最佳效果。三者对角加速度估计结果如图7 所示,其中虚线为真实值,红色实线为互补滤波方法估计结果,蓝色虚线为卡尔曼滤波方法估计结果,绿色点线为对角速度直接微分后低通滤波的估计结果。

图7 角加速度估计结果Fig.7 Angular acceleration estimation results
低通滤波方法虽然抑制噪声的效果很好,但其时间延迟较大,卡尔曼滤波方法虽然可以实时计算最优卡尔曼增益,但由于其计算角加速度预测值时采用了线性模型,在姿态变化剧烈时测量值与预测值误差较大,也导致了时间延迟较大。与卡尔曼滤波和微分后低通滤波方法相比,互补滤波方法虽然计算量更大,但其抑制噪声的能力更强,时间延迟也更小。 因此,在实现高机动轨迹跟踪控制时,采用互补滤波方法获得角加速度反馈以提高INDI 方法的精度。
3 飞行试验
为了验证本文所设计控制器的精度和抗扰性能,采用图1 中所示四旋翼无人机进行飞行试验。该四旋翼重667 g,推进系统由T-MOTOR F1507 3 800 kV 电机、T-MOTOR T3140 桨叶和T-MOTOR V45A V2 电调组成,相邻电机相距15 cm,由一个4S LiPo 电池供电。 飞控选用Pixraptor,控制频率为250 Hz,飞机的姿态、角速度、加速度等由其内部IMU 测量得到,位置信息由120 Hz 的OptiTrack动作捕捉系统提供。 利用EKF 方法对OptiTrack 的位置信息和IMU 的加速度信息进行处理融合,得到融合后的位置、速度和加速度信息,根据试验选择延迟最小、精度最高的互补滤波方法对角加速度进行估计。
首先,使跟踪速度和加速度都很大的高机动轨迹验证其对高机动轨迹的跟踪能力;其次,通过附加超过飞行器正面面积4 倍以上的纸板增大飞行过程中的阻力,增大其模型误差,验证其对内部干扰的鲁棒性;然后,利用风扇测试其在5 m/s 的风干扰中的悬停能力,进一步展示了对外部干扰的鲁棒性;最后,将设计的控制器性能与常规PID控制器进行对比分析。
3.1 轨迹跟踪试验
为了保证试验的安全,轨迹跟踪的起始和终止状态飞机应保持悬停,根据参考文献[27]中的Minimum snap 方法,设计了不同加速度、速度的8 字形参考轨迹,分别利用前馈PID 方法和本文所设计的前馈INDI 方法对其进行跟踪。 当参考轨迹的最大速度为4. 481 m/s,最大加速度为5.117 m/s2时,前馈PID 方法和前馈INDI 方法均能很好地跟踪参考轨迹,但前馈INDI 方法跟踪的均方根误差远小于前馈PID 方法。 试验结果如图8和表1 所示。
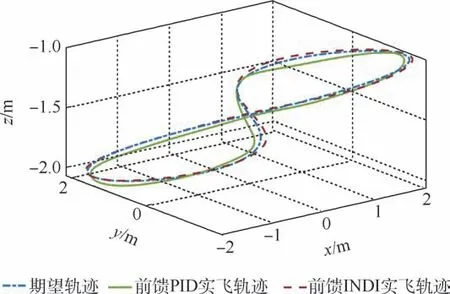
图8 低速轨迹跟踪曲线Fig.8 Low speed trajectory tracking curves
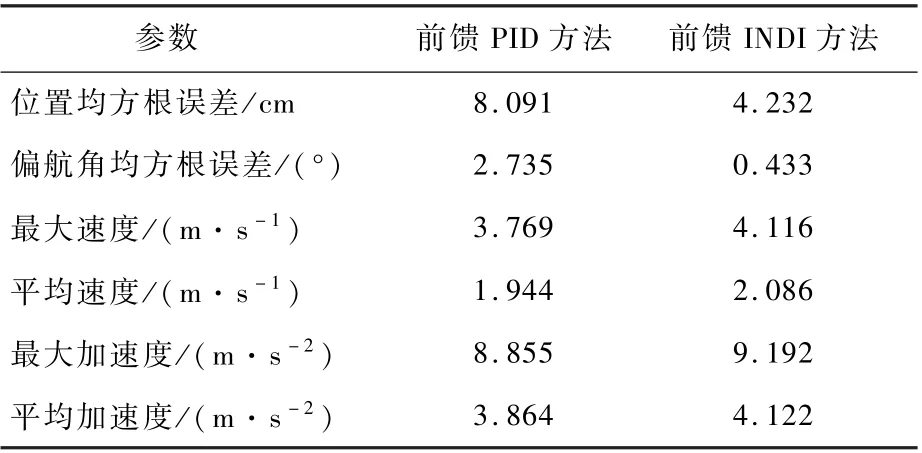
表1 低速轨迹跟踪效果Table 1 Low speed trajectory tracking performance
在跟踪最大速度为6. 098 m/s、最大加速度为12.648 m/s2的8 字形轨迹时,前馈PID 方法的跟踪误差为17.238 cm,而前馈INDI 方法仅为7.175 cm。 此时,前馈PID 方法控制飞行器进行轨迹跟踪时,姿态较为振荡,稳定性下降。 试验结果如图9和表2 所示。
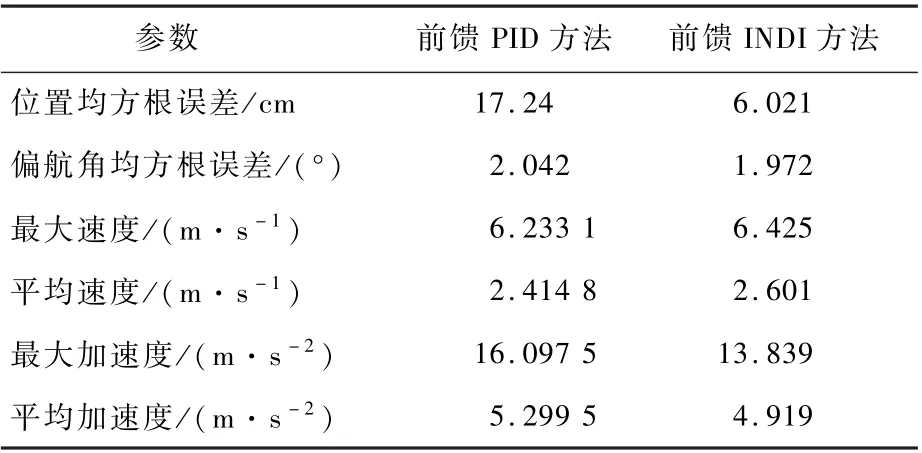
表2 中速轨迹跟踪效果Table 2 Medium speed trajectory tracking performance

图9 中速轨迹跟踪曲线Fig.9 Medium speed trajectory tracking curves
当参考轨迹的速度和加速度进一步提高时,前馈PID 方法无法跟踪,而前馈INDI 方法仍然能保持很高的精度。 采用不同的角加速度估计方法跟踪最大速度10.18 m/s、最大加速度15.36 m/s2的参考轨迹时,跟踪结果如图10 所示,飞行过程中的位置误差、偏航角误差、速度和加速度曲线如图11所示,试验数据如表3 所示。
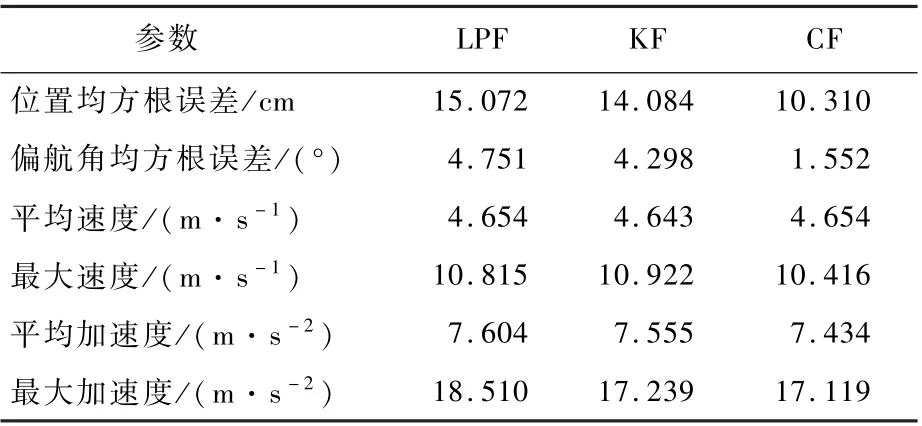
表3 高机动轨迹跟踪效果Table 3 Aggressive trajectory tracking performance
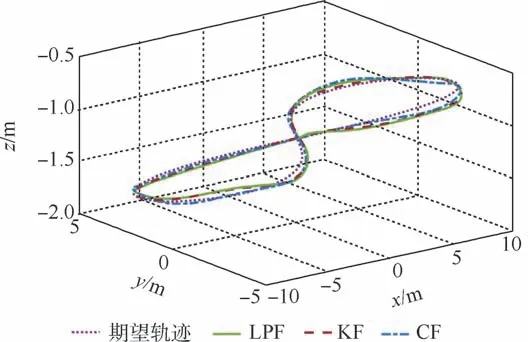
图10 高机动轨迹跟踪曲线Fig.10 Aggressive trajectory tracking curves
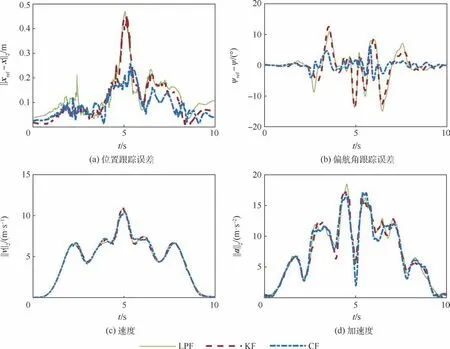
图11 高机动轨迹跟踪曲线Fig.11 Aggressive trajectory tracking curves
跟踪过程中,基于互补滤波的前馈INDI 控制方法的跟踪误差仅为10.310 cm,偏航角的均方根误差为2.645°。 飞行器的最大速度为10.416 m/s,平均速度为 4. 654 m/s, 最大加速度为17.119 m/s2,平均加速度为7.434 m/s2。 可见设计的基于互补滤波的前馈INDI 控制器可以跟踪高机动轨迹,有着较高的精度。
3.2 抗扰试验
3.2.1 内部干扰
在飞机下方悬挂如图12 所示面积大于其4 倍的硬纸板,增大其运动时的空气阻力,增大其与仿真模型的不匹配度,以测试该控制器对内部模型误差干扰的鲁棒性。

图12 悬挂纸板的四旋翼无人机Fig.12 Quadrotor with cardboard drag plate
分别用微分平坦前馈PID 控制器和本文所设计的控制器控制四旋翼跟踪最大速度4.07 m/s、最大加速度8. 45 m/s2的轨迹,效果如图13 所示,飞行过程中的位置误差、偏航角误差、速度和加速度曲线如图14 所示。
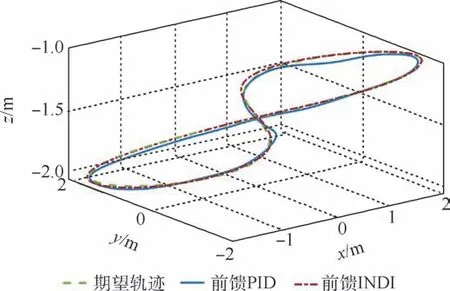
图13 带纸板轨迹跟踪曲线Fig.13 Tajectory tracking curves with cardboard drag plate
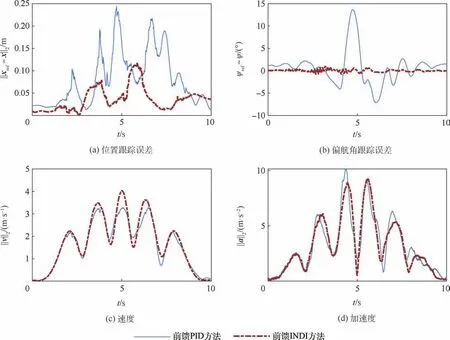
图14 带纸板轨迹跟踪曲线Fig.14 Trajectory tracking curves with cardboard drag plate
前馈PID 控制器跟踪该轨迹时,均方根误差为8. 091 cm,但加入纸板后,均方根误差变为10.00 cm,精度有所下降。 前馈INDI 控制器跟踪轨迹时,均方根误差为4.232 cm,加入纸板后为4.494 cm,变化不明显。 其他参数如表4 所示。 可见,前馈INDI 控制器不仅精度更高,对模型误差的容忍性也更强,对内部干扰有着优秀的抗扰能力。
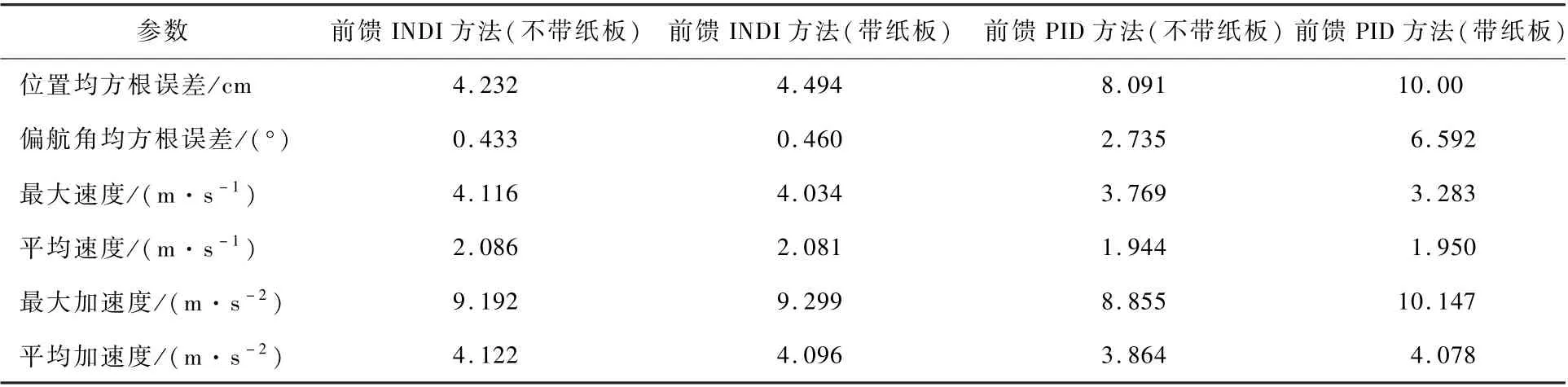
表4 轨迹跟踪效果Table 4 Trajectory tracking performance
3.2.2 外界干扰
为了验证前馈INDI 控制器对外界干扰的抗扰能力,将功率为280 W 的华生FL750 工业风扇置于飞机悬停点前方2 m 处(见图15),用风速仪测得此处风速约为5 m/s,进行悬停抗扰试验,得到的悬停效果如图16 所示。

图15 悬停抗扰试验Fig.15 Hover test with disturbance

图16 悬停抗扰曲线Fig.16 Curves for hover with disturbance
前馈PID 控制器控制四旋翼进行悬停时,风扇启动后位置和偏航角误差都显著增大,位置最大误差达12.273 cm。 前馈INDI 控制悬停加入风干扰后,位置误差虽有所增大,但位置误差最大时也仅为4. 502 cm,风干扰对其悬停的影响不大。 可见对于外界干扰,前馈INDI 方法的鲁棒性明显优于前馈PID 方法。 其他参数如表5所示。
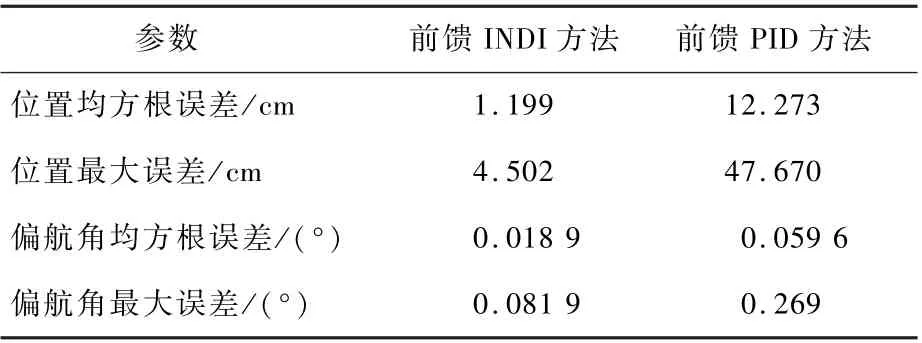
表5 悬停抗扰效果Table 5 Performance for hover with disturbance
综上所述,不论是对于建模不准确引起的内部干扰,还是外界阵风干扰,前馈INDI 方法都表现出了优秀的抗扰能力。
4 结 论
1) 设计的前馈INDI 控制器在跟踪高机动轨迹时具有较高的控制精度,在跟踪最大速度为10.416 m/s,最大加速度为17.119 m/s2,平均速度为4.654 m/s,平均加速度为7.434 m/s2的高机动轨迹时,均方根误差仅为10.310 cm。
2) 该控制器对内部扰动具有较强的抗扰能力,加入纸板增大模型误差后,跟踪最大速度为4.034 m/s,最大加速度为9.299 m/s2的轨迹时,均方根误差由4.232 cm 变为4.494 cm,无明显增大。
3) 该控制器对外界风干扰具有较强的抗干扰能力,令控制器控制飞行器保持悬停,在其悬停正前方2 m 处引入风速为5 m/s 的风干扰,位置均方根误差仍能保持在1.199 cm。
飞行试验表明,本文设计的基于互补滤波的前馈INDI 轨迹跟踪控制器可以控制飞行器精准、快速跟踪参考轨迹,在高机动飞行时仍保持极高的控制精度,对外界风干扰和内部模型误差有着较强的抗扰能力。
