斧形齿破岩机理数值模拟研究*
2022-10-13龚均云吴文秀周宗赣
龚均云 吴文秀 周宗赣
(长江大学机械工程学院)
0 引 言
PDC钻头广泛用于石油、天然气及煤炭等领域的软中硬岩钻探中,目前已占据市场主导地位[1]。然而,在高研磨性、硬地层钻井时,传统PDC钻头切削齿经常遭遇碎裂、压裂、磨损等损伤,这很难满足深地层非常规资源的勘探要求[2]。
近年来,随着PDC切削齿的加工技术不断的进步,PDC切削齿表面的金刚石层不再局限于平面,非平面PDC切削齿应运而生,如锥形齿、斧形齿、三棱齿和波形齿等。在2016年,斯伦贝谢公司推出了Axe-blade 屋脊齿,由于其金刚石层类似于斧头,也称之为斧形齿,相比于传统PDC切削齿,其耐磨性和抗冲击性得到明显提升[3-6],寿命也显著延长。
到目前为止,国内外研究人员针对斧形齿破岩进行了多方面研究。SHAO F.Y.等[7]利用 vertical turret lathe(VTL)对斧形齿与常规切削齿进行比较试验,试验结果表明,斧形齿比传统平面齿具有更好的耐磨性和切削效率,并且消耗的能量比传统平面齿要小;LOMOV等采用有限元分析(FEA)软件对斧形齿和传统平面齿进行模拟,研究发现,在不同的地层,在给定的切削深度下,斧形齿比传统切削齿所需的切削力更小。谢晗等[8]利用有限元软件,模拟了非平面齿在含砾石和软硬交错地层的切削过程,结果表明,斧形齿的接触更平稳,破岩效率更高,切削力以及切削力波动幅度比常规切削齿小。李乾等[9]通过分析斧形齿的性能优势,研制出斧形齿PDC钻头,并将其应用于东海深部地层钻进,结果表明,相比常规PDC钻头,斧形齿PDC钻头机械钻速明显增加,钻井周期缩短,经济效益显著。赵润琦等[2]利用有限元数值模拟的方法,分析斧形齿破岩特性,并与常规PDC切削齿比较,斧形齿更容易吃入地层,在相同的情况下,破岩比能更小,破岩效率更高。
目前,国内外对于斧形齿的研究大多集中在与常规平面齿的对比方面,关于斧形PDC切削齿的切削工艺参数方面的研究较少。因此,笔者基于弹塑性力学与岩石力学,以Drucker-Prager准则作为岩石的屈服准则,利用有限元软件建立三维数值仿真模型,研究了齿面角、后倾角、切削速度和切削深度等因素对斧形齿破岩规律的影响,从而进一步优化斧形齿PDC钻头的布齿,提高钻井效率,缩短钻井周期。
1 破岩性能评估与岩石本构关系
1.1 斧形PDC切削齿受力分析与破岩性能评价指标
斧形PDC切削齿在破碎岩石的过程中,受到的力可分解为切向力Fh、轴向力Fn以及齿面法向力Ff,其中Fh与切削速度相反,Fn与Fh方向相互垂直,Ff与Fn的夹角为α。当单个切削齿以恒定的速度切削时,其受力如图1所示。

图1 斧形PDC切削齿受力图Fig.1 Stress diagram of axe-shaped PDC cutter
图1中:φ为斧形齿的齿面角;d为切削的距离;v为斧形齿的切削速度;h为切削深度;α为后倾角。
在破岩过程中,破岩比功PMSE是计算破岩效率的关键指标,是指破碎单位体积所需的能量,表达式如下:
(1)
式中:W为破碎岩石所需要的功;V为破碎岩石的体积。
对于单个切削齿,如果切削距离为d,岩石断口截面面积为S,那么式(1)就可写成
(2)
1.2 岩石强度标准与失效准则
岩石是一种不均匀的各项异性材料,选择有效的岩石本构模型是模拟岩石切削的前提,目前通常采用Drucker-Prager(D-P)模型来描述岩石塑性阶段下的本构关系。D-P准则是在Mises和Mohr-Coulomb(M-C)准则基础上拓展而来的,其表达式如下:
(3)
I1=σ1+σ2+σ3
(4)
(5)
(6)
(7)
式中:I1为第一不变量的应力量;J2为第二不变量的应力偏量;λ和K是与岩石内摩擦角β和黏结力C有关的试验常数;σ1、σ2、σ3分别为第一、第二、第三主应力。
岩石破坏过程中的应力-应变关系见图2。

图2 岩石破坏过程中的压力-应变曲线Fig.2 Pressure-strain curve during rock failure

2 单齿切削破岩有限元模型建立
2.1 有限元仿真方案
为研究斧形齿切削工艺参数对切削效果的影响,并分析斧形齿的破岩机理,通过在ABAQUS装配模块改变后倾角α等,设置不同的边界条件,使斧形齿在不同的状态下切削岩石。具体方案如表1所示。

表1 仿真计算方案Table 1 Simulation calculation scheme
2.2 仿真的基本假设与模型简化
由于井下环境复杂,为了方便计算,做出如下假设与简化[10-16]:
(1)将PDC切削齿当作刚体,不考虑切削齿的磨损;
(2)不考虑温度、钻井液射流对岩石的影响,且假设岩石为均质、各向同性介质;
(3)被切削的岩石单元立刻失效,不影响后面的切削;
(4)岩石模型周围及底部属于井眼远场部分。
2.3 模型参数设置
利用三维软件UG完成几何模型的建立,如图3所示。

图3 斧形齿与岩石三维几何模型Fig.3 3D geometric model of axe-shaped cutter and rock
斧形齿的基本尺寸为ø13.44 mm×13 mm,齿面角φ根据表1的仿真试验方案来确定,岩石尺寸为50 mm×45 mm×20 mm。
将斧形齿绕轴线的旋转切削转化为以速度为v、切削深度为h、后倾角为α的直线切削。切削速度、后倾角及切削深度根据表1的仿真方案来确定。斧形齿与岩石材料参数如表2所示。

表2 有限元模型材料参数Table 2 Material parameters of finite element model
在ABAQUS中为模型赋予相应的材料,并根据剪切损伤准则,定义损伤系数,模拟岩屑并在失效之后及时删除网格单元。斧形齿与岩石的接触为非线性接触,为体现出切削效果,将斧形齿表面与被切削岩石采用面与节点集相互作用,并将金刚石设置为刚体。为提高计算效率,在斧形齿与岩石相互作用处细化网格。岩石网格单元采用C3D8R六面体单元,缩减积分,沙漏控制,岩石的单元数量107 100;斧形齿采用C3D10M十节点四面体网格,结果如图4a所示。对岩石下部以及两边施加固定约束,对斧形齿施加上表1的速度,并限制除速度方向的其他方向移动,结果如图4b所示。

图4 斧形齿切削有限元模型Fig.4 Finite element model for cutting of axe-shaped cutter
3 仿真结果与讨论
3.1 齿面角对切削过程的影响
从斧形齿结构上看,齿面角无疑是斧形齿能高效破岩的关键参数之一。齿面角对切削过程的影响如图5所示。
由图5可知:切向力随着齿面角的增大而增大,并且随着切削深度的增加,切向力也不断增大;从增长的幅度来看,切削深度的影响大于齿面角的影响。另外,齿面角对破岩比功无明显的影响规律,但随着切削深度的增加,斧形齿破岩比功开始变小,并且切削深度由1 mm增大到2 mm比从2 mm增大到3 mm破岩比功变化幅度小。随着齿面角的不断增大,切向力标准差呈现起伏波动,但整体的趋势是随着齿面角的增大而增大。切削深度的增大,进一步加大了切削力的波动。当切削深度为1 mm时,随着齿面角的增大,切向力标准差较小,增长较为平缓;当切削深度达到2 mm时,标准差开始增大;当切削深度达到3 mm时,标准差成倍增加;此时破岩比功较小,破岩效率较高,但此时的切削力所受的波动也增大,破岩过程平稳性变差,可能导致斧形齿的寿命缩短。

图5 齿面角对斧形齿切向力、破岩比功和切向力标准差的影响Fig.5 Effects of ridge angle on tangential force,specific work of rock breaking and standard deviation of tangential force of axe-shaped cutter
斧形齿轴向力(平均值)与轴向力标准差如图6所示。从图6a可以看出,轴向力明显小于切向力,随着齿面角和切削深度的增加,轴向力也随之增大,这会导致随着齿面角的增大斧形齿吃入能力减弱,在相同的工况下,齿面角增大会导致钻压也随之增加。由图6b可以看出,切削深度对轴向力标准差的影响比齿面角的变化更大,总体呈现上升趋势。当切削深度大于2 mm时,标准差急剧增大,切削时振幅越大,这会导致斧形齿寿命缩短,破岩效率降低。
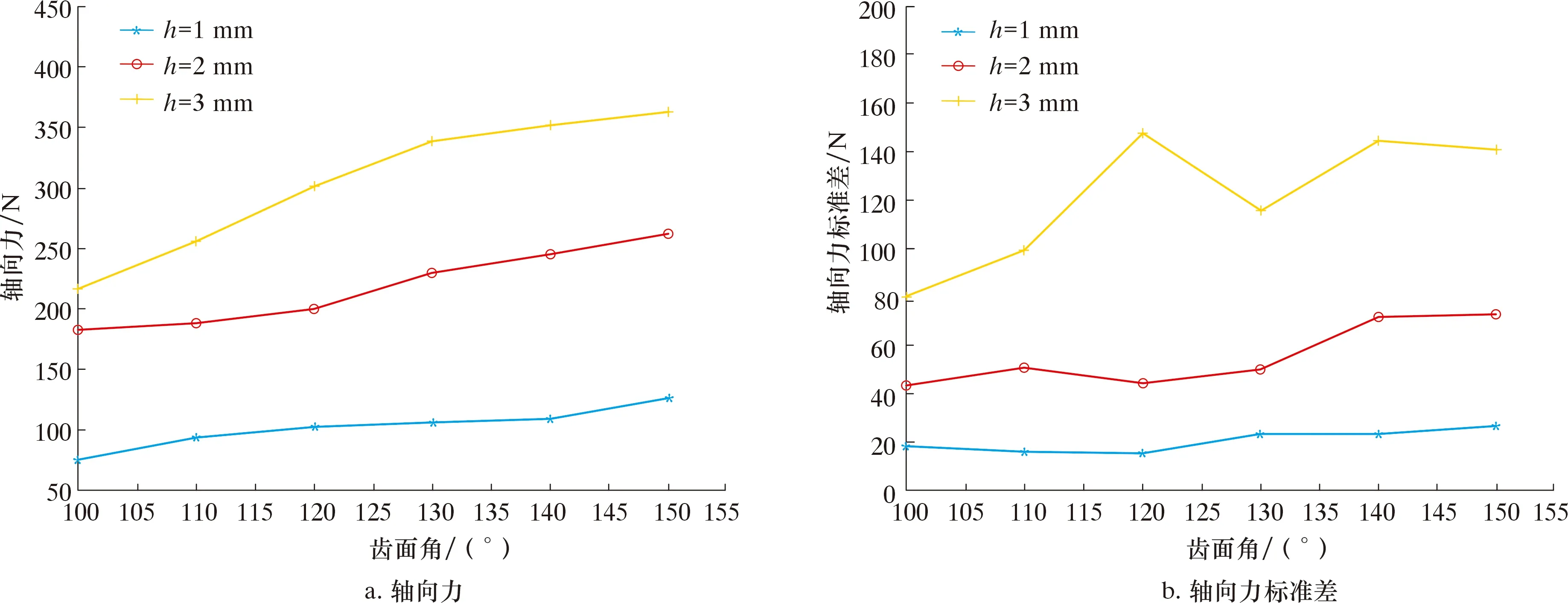
图6 齿面角对斧形齿轴向力和轴向力标准差的影响Fig.6 Effects of ridge angle on axial force and standard deviation of axial force of axe-shaped cutter
图7为斧形齿在2.5 m/s的切削速度、后倾角15°、切削深度2 mm的条件下切削时,不同齿面角的齿面接触应力云图。从整体上看,只有与岩石接触的地方有接触应力,其他区域的接触应力为0。在接触区域内,斧形齿的接触应力主要集中在棱脊附近。这是由于在破岩过程中,斧形齿先以棱脊的集中力入侵岩石,引起岩石的塑性变形,随后两边的齿面才慢慢开始接触岩石,所以棱脊处的应力远大于两边齿面的应力。正因如此,斧形齿的磨损会由棱脊的下面开始,直到切削齿慢慢失效,导致破岩效率降低。当齿面角从100°增加到150°时,齿面接触应力开始由棱脊的应力集中慢慢向两边扩散。由于齿面角的增大,两边的齿面开始为中间的棱脊承担破岩压力,导致棱脊处的压力减小,并且由于齿面角的增大,接触区域上方的应力也在慢慢增加,进一步分担了棱脊处破岩的压力。

图7 不同齿面角下齿面接触应力云图Fig.7 Contact stress of cutter surface at different ridge angles
图8为对应图7条件下,切削过程中岩石的塑性应变云图。
从整体上看,岩石发生最大的塑性变形集中在中间的切削区域,两边的塑性变形较小。这是由于斧形齿的棱脊先与岩石相互接触,导致岩石产生了局部裂缝,岩石的内应力得到释放,随后两边的齿面与岩石接触,并使岩石发生倾斜。因此在破碎和剪切的联合作用下,前面的岩石迅速破碎,最终形成如图8所示的塑性变形区。当齿面角慢慢增大时,中间塑性变形区的颜色慢慢变浅,区域有向两边扩散的趋势。
3.2 后倾角对切削过程的影响
后倾角对切削过程的影响如图9所示。由图9可知:后倾角的变化对切向力无显著影响,但破岩比功随着角度的增大有上升的趋势;随着切削深度的增大,切向力增大而破岩比功减小;切向力标准差随着切削深度增加而增大。

图9 后倾角对斧形齿切向力、破岩比功和切向力标准差的影响Fig.9 Effects of back rake angle on tangential force,specific work of rock breaking and standard deviation of tangential force of axe-shaped cutter
后倾角对斧形齿轴向力(平均值)与轴向力标准差的影响如图10所示。由图10可以看出,后倾角对轴向力的影响明显大于切向力。随着后倾角和切削深度的增大,轴向力明显呈现上升的趋势。在切削深度较浅时,轴向力标准差的波动较小,与后倾角无显著关系;但随着切削深度的增加,在后倾角大于15°时,轴向力标准差快速增大,轴向力越来越不平稳,导致破岩效率减低,切削齿寿命也会大幅度缩短。切削齿的失效从本质上会导致PDC钻头的失效,使钻井成本大幅增加,钻井周期延长。

图10 后倾角对斧形齿轴向力和轴向力标准差的影响Fig.10 Effects of back rake angle on axial force and standard deviation of axial force of axe-shaped cutter
3.3 切削速度对切削过程的影响
设置切削速度分别为1.0、1.5、2.0、2.5和3.0 m/s,以齿面角130°、后倾角15°,在3个切削深度(1、2和3 mm)下进行数值模拟,结果如图11所示。从图11可以看出,切向力与破岩比功随着切削速度增大而增大,在给定的条件下,当切削速度大于2 m/s时,切向力和破岩比功的增长开始逐渐平稳,而切向力标准差却有上升的趋势。随着切削深度的增加,切向力与切向力标准差均增大,破岩比功却不断减小。
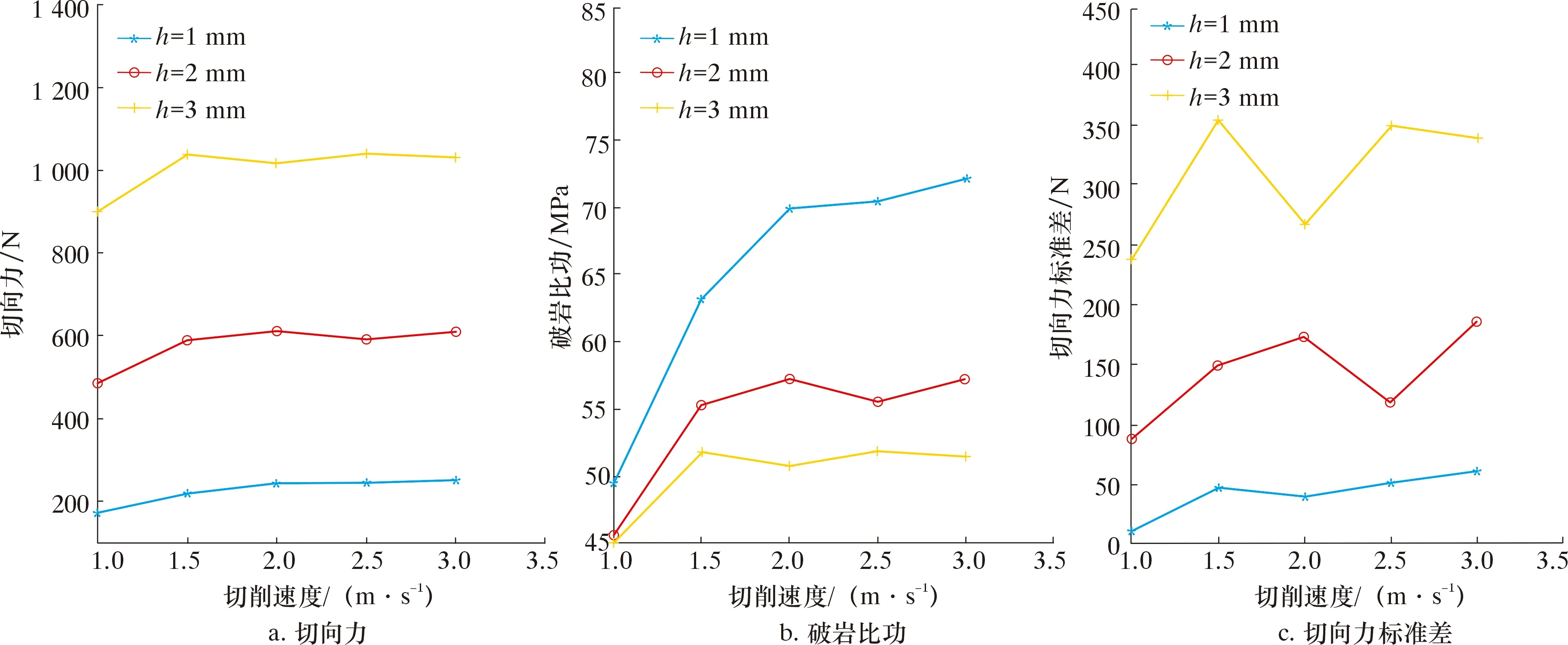
图11 切削速度对斧形齿切向力、破岩比功和切向力标准差的影响Fig.11 Effects of cutting speed on tangential force,specific work of rock breaking and standard deviation of tangential force of axe-shaped cutter
4 结论及建议
(1)在后倾角15°、切削速度2.5 m/s的情况下,斧形齿的切向力、轴向力都随着齿面角和切削深度的增大而增大,破岩比功随着切削深度的增大而减小,破岩效率也越高,但随着切削深度的增大,切向力和轴向力的波动也越来越大。
(2)在齿面角130°、切削速度2.5 m/s的情况下,后倾角对斧形齿轴向力的影响比切向力大,随着后倾角的增大,轴向力和破岩比功均增大,设计时应选择较小的后倾角。
(3)在齿面角130°、后倾角15°的情况下,以不同的切削速度切削岩石,切向力、破岩比功均随着速度的增加而增大。
(4)从模拟结果来看,随着切削深度的增加,斧形齿的轴向力与切向力的波动均大幅度上升,稳定性变差,破岩比功不断减小。综合考虑,为了使斧形齿有较好的切削性能,建议将切削深度选取为2 mm左右。
