成组序贯设计中基于实际信息量的临界值校正方法的比较研究*

南方医科大学公共卫生学院生物统计学系(510515)

傅利强 陈思敏 吴海燕 谭旭辉Δ

【提 要】 目的 在大样本条件下，比较成组序贯设计中基于实际信息量的不同临界值校正方法之间的差异。方法 基于O′Brien-Fleming(OBF)法和指数损耗函数法，通过设定不同的参数以及匹配条件，比较线性插值校正法、OBF损耗函数校正法、指数损耗函数校正法之间的I类错误α和功效Power的差别。结果 当设计方法为OBF法和指数损耗函数法(ρ=2)时，与之相匹配的OBF损耗函数校正法、指数损耗函数校正法(ρ=2)以及线性插值校正法均能将I类错误控制在0.05，功效Power控制在0.9；当设计方法为指数损耗函数法(ρ=1或ρ=3)时，与设计方法不匹配的校正方法仍可将I类错误维持在0.05左右，但功效Power明显偏离0.9。结论 在进行成组序贯期中分析时，线性插值校正法作为通用方法能够适用于各类设计，损耗函数校正法只适用于已知损耗函数形式的设计。

随着临床试验的不断发展，研究者对试验的设计需求不断提高。成组序贯设计由于具有早期终止试验，节约样本量[1]等优点，逐渐被广泛应用[2-3]。成组序贯设计本质特征是对试验过程中累积资料分阶段进行多次期中分析，直到以一定的显著性水准拒绝或不拒绝原假设而终止试验。然而在实际应用时，由于每阶段的实际信息量与理论信息量并不相同，从而在进行期中分析时必须对每阶段的临界值进行调整，其中最常用的方法就是通过实际信息量去校正临界值，即基于实际信息量的临界值校正方法。其原理是通过实际信息量去调整每阶段的临界值，并使得最终的显著性水平满足设定值。但是目前的研究中，尚未有关于各个基于实际信息量的临界值校正方法之间对比研究的论述，因此本文将会通过模拟比较各种基于实际信息量的临界值校正方法，为研究者在进行成组序贯期中分析时，对相关临界值校正方法的选择提供理论参考。

方法原理

成组序贯设计(group sequential design)因具有良好的灵活性和经济性等设计特性备受人们关注，而实现这些特性最重要的方法基础是对α或β损耗过程的调整。损耗过程设计方法分为固定边界值法[4]、损耗函数法[5]以及自定义损耗过程，对应的基于实际信息量的临界值校正方法有线性插值校正法和损耗函数校正法，其中最常用的损耗函数校正法有指数损耗函数校正法、O′Brien-Fleming(OBF)损耗函数校正法，方法原理如下。

1.线性插值校正法

线性插值法由Kittelson等人于1999年提出[4]，其提出的初衷就是想解决成组序贯不同设计间如何校正临界值以确定停止规则的问题。其原理是基于实际信息量利用两个相邻期中分析阶段的累计理论损耗错误进行插值计算，近似得到实际错误损耗的变化趋势，公式如下：

其中αj为第j阶段的设计损耗I类错误α或II类错误β，e1，e2，…，eK为设定的第1至K阶段的累积损耗I类错误或II类错误，e(I)为校正后的累积损耗错误，Ij为第j阶段的设计信息量，I为实际信息量。

2.OBF损耗函数校正法

OBF设计[6]如前文所述，原属于固定边界值方法[7]，即预先设定边界值和名义检验水准，其灵活性在实际应用中受到限制，故在损耗函数法中发展出了其近似的损耗函数形式，OBF损耗函数如下所示：

其中t为信息比，a为设计中设定的α或β，Φ是Z统计量的累积分布函数，对于给定的α或β，第k阶段的累积错误损耗为αE(Πk；α)或βE(Πk；β)，式中Πk=Ik/IK为第k阶段设计信息量与最大信息量之比。

OBF损耗函数校正法则是基于实际信息量进行损耗调整[8]，从而改变各阶段的临界值，即在计算时，将Πk=Ik/IK中的第k阶段理论信息量Ik替换为实际信息量I，公式如下：

公式中IK为设计时理论最大信息量，计算得到的e(I)为校正后的累积错误损耗。

3.指数损耗函数校正法

OBF法作为经典的方法，其特点是较为保守。而指数损耗函数法[5]相较于OBF法，虽然可能损失了较多检验效能，但是其能够在试验早期以较大可能拒绝原假设使得试验提前结束。例如，二次方损耗函数在现实应用中就因为其拒绝早而损失的检验效能较少而被广泛推荐应用。指数损耗函数[9]公式如下：

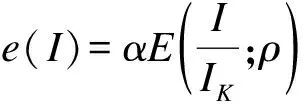
模拟比较

本文的模拟研究以成组序贯设计中最常用的两样本均数比较作为设计框架，其原假设和备择假设为：H0：θ=0，H1：θ>0(δ=2)，模拟设定的I类错误为0.05，功效为90%，即α=0.05，β=0.1。成组序贯试验阶段数K为3，试验组均值Mt=5或7，对照组均值Mc=5。由于指数损耗函数法和OBF法是比较常用的期中分析方法，故本文选用OBF法与指数损耗函数法作为设计方法。试验样本量为每组每阶段50例和100例。这里需要指出的是，当试验设计终止规则为拒绝型(reject)时(即期中分析只能以拒绝H0而终止试验)，只有I类错误α在期中分析过程中损耗；当设计为接受型(accept)时(即期中分析只能以接受H0而终止试验)，只有II类错误β在期中分析过程中损耗。为了探讨校正方法对α和β的影响，我们将在拒绝型和接受型设计下，分别比较两种方法相对应的基于实际信息量的临界值校正方法之间的区别与联系。随后，进一步对校正方法的错误应用情况进行分析，探究校正方法错误使用时的影响。模拟程序基于SAS 9.4软件实现，为了确保得到稳定的结果，模拟次数设定为50000次。

1.校正方法正确匹配时的参数设置

在上文设定的条件下，基于OBF法和指数损耗函数法(ρ=2)来研究和比较临界值校正方法之间的差异，其中OBF法对应的校正方法为线性插值法和OBF损耗函数法，指数损耗函数法对应的校正方法为线性插值法和同形式的损耗函数法。根据以上参数设定分别求其50000次模拟下拒绝型设计的I类错误α以及接受型设计的功效Power。第一部分模拟试验的参数设置如表1所示。

表1 校正方法正确匹配时参数设置

2.校正方法错误匹配时的参数设置

为了对损耗形式与校正方法不匹配的情况进行研究，我们以ρ=3和ρ=1的指数族损耗函数为设计方法，通过模拟分别计算I类错误α以及功效Power，相应的参数设置如表2所示。

表2 校正方法错误匹配时参数设置

结 果

1.校正方法正确匹配时的结果

按照表1中设置的参数，通过模拟我们得到的I类错误α和功效Power，如表3所示。由表3中的结果可知，无论是OBF法还是损耗函数法，其相同形式的损耗函数方法和线性插值校正法均较好地维持住了I类错误α以及功效Power，线性插值法校正后的效果略差，但随着样本量的增加，差异可以忽略不计。同时我们也可以看到，在样本量为50的情况下，指数损耗函数法(ρ=2)的I类错误α有轻微的膨胀，而在样本量为100时I类错误就能稳定在0.05附近。

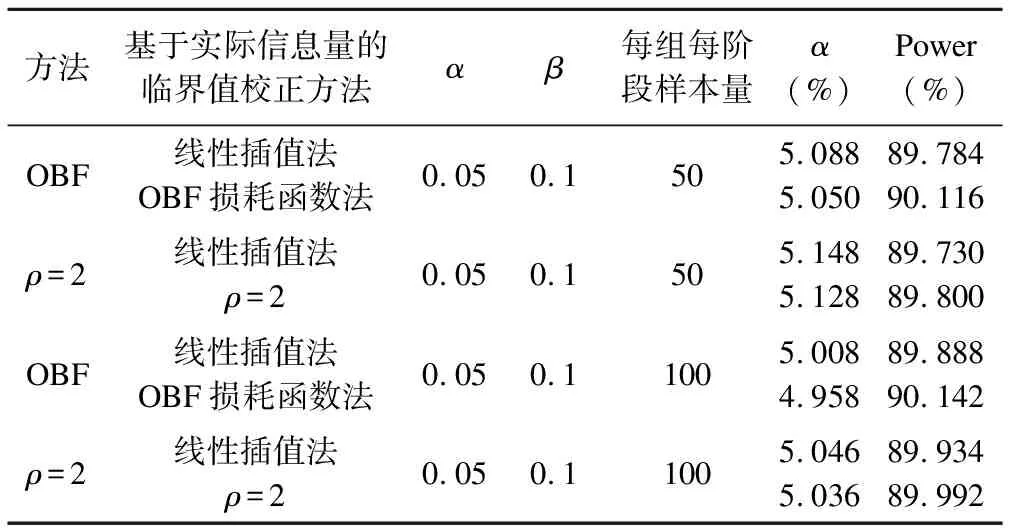
表3 校正方法正确匹配时的结果

2.校正方法错误匹配时的结果

根据表2的参数设置，校正方法错误匹配时的结果如表4所示。从表4中我们可以看到在校正方法错误匹配的情况下，两种对应方式的I类错误虽然有轻微的波动，但还是能大致稳定在0.05附近。反观两种对应方式的功效Power有明显的下降或上升情况，偏离试验设定的预期功效值0.9。

表4 校正方法错误匹配时的结果

讨 论

本文所研究的是成组序贯试验中采用不同的基于实际信息量的临界值校正方法对期中分析以及最终结果的影响。为此进行了两部分的模拟研究，并对模拟结果进行了分析比较。

模拟结果显示，无论OBF法还是指数族损耗函数法，其对应的损耗函数校正法和线性插值法均可以较好地维持I类错误α和功效Power。在样本量为50的情况下，指数损耗函数法(ρ=2)的I类错误α有轻微的膨胀，这是由于该设计第一阶段的样本量不够大[10]，同时该方法早期拒绝概率比OBF法更高[11]。因此，当样本量为100时I类错误就能稳定在0.05附近。而对于线性插值法的适用性，分析其方法原理可知，线性插值法通过线性插值拟合试验设计方法设定的α或β损耗过程，得到一个近似的损耗形式去校正临界值，较好地保持了试验设计的I类错误α和功效Power，由此适应各种损耗形式情况下的校正需求，这也证明了SAS软件将该方法设定为默认选项的合理性。另外，OBF虽然是固定边界值法，依然可以采用相对应的OBF损耗函数校正法去进行临界值校正。由此可推知，在进行临界值校正时，当α或β损耗形式已知时，其相同损耗形式的校正方法和线性插值法均可以使用，而从设计需求方面考虑，与损耗形式相同的校正方法能更好的保持原设计特性，更符合设计需求，应当成为校正方法的首选。

另一方面，当临界值校正方法与设计方法不匹配时，由于试验的设计特性是优先保证试验的α，因此I类错误依然可以相对稳定控制，但是功效Power则会受到较大影响，这是由于在指数损耗函数法(ρ=3)的情况下，指数损耗函数法校正法(ρ=1)所需的最大信息量与设定损耗函数(ρ=3)所需的最大信息量不符(即指数损耗函数校正法ρ=1时所需的最大样本量大于设定损耗函数ρ=3时所需的最大样本量)，从而使得检验功效Power不足。反之，当校正方法所需的最大信息量小于设定损耗函数方法所需的最大信息量时，检验的总体功效Power则会上升。由此可见，当临界值校正方法选择错误的时候，期中分析的功效会受到严重影响。因此，当损耗函数形式未知或自定义损耗形式时，线性插值校正法是唯一可以适用的方法，该方法通过对损耗过程的近似拟合来进行临界值校正，不受未知损耗函数形式的影响。

综上所述，在进行成组序贯期中分析时，基于实际信息量的临界值校正方法选择准则如下：当试验设计的损耗函数形式已知时，选择相同损耗形式的临界值校正方法；当损耗函数形式未知或自定义损耗形式时，选择线性插值校正法；当试验设计为固定边界值法时，其相似的损耗函数形式校正法与线性插值校正法效果相近。