矿用千米定向钻机动作识别方法
2022-10-12向学艺雷志鹏栗林波任瑞斌李杰王飞宇
向学艺,雷志鹏,栗林波,任瑞斌,李杰,王飞宇
(1. 太原理工大学 矿用智能电器技术国家地方联合工程实验室, 山西 太原 030024;2. 太原理工大学 煤矿电气设备与智能控制山西省重点实验室, 山西 太原 030024;3. 晋能控股山西科学技术研究院有限公司(晋城)技术中心,山西 晋城 048000;4. 山西金鼎高宝钻探有限责任公司,山西 晋城 048000)
0 引言
近年,煤炭行业正迈入智能化转型的关键期,八部委在《关于加快煤矿智能化发展的指导意见》中倡导煤炭行业与现代信息技术高度结合,实现煤矿管理无人化、煤炭生产智能化的发展目标[1]。矿用千米定向钻机是实现煤炭智能化生产必备的装备。然而目前千米定向钻机的行走、钻进等各项操作均由司钻工人手动操作实现,钻进效率与司钻工人经验水平和操控熟练程度密切相关,严重制约了煤层气抽采效率和煤矿智能化发展进程。因此,远程识别钻机各项动作和智能操控钻机运行成为实现这一发展目标必须解决的难题。
矿用千米定向钻机的动作主要包括动力头不带钻杆旋转、带钻杆旋转、带钻杆向前慢速钻进、带钻杆向前快速钻进、带钻杆慢速后退、带钻杆快速后退等类型。液压泵站作为千米定向钻机的动力源,为其实现各项动作提供能量。液压泵站为千米定向钻机提供动力的过程中会产生一系列与千米定向钻机当前执行动作密切相关的振动信号,如能从这些振动信号中提取某些特征量,就能识别液压泵站运行状态,从而实现钻机动作类型识别[2],对于远程掌握千米定向钻机状态,促进千米定向钻机控制技术的智能化发展具有重要意义。但液压泵站上的振动信号往往呈现出非线性、非平稳、低信噪比等特点,提取这类信号的特征量比较困难,为此不少研究者进行了大量的研究工作。李洪儒等[3]、姜万录等[4]、郑直等[5]分别利用改进多尺度熵故障特征提取方法、递归定量法和对数-频谱振幅调制方法提取液压泵振动信号特征值,能够有效判别液压泵的运行状态,但这些方法多是针对液压系统某一部件在单一工况下的振动信号分析,对液压泵站其他部位(如电动机和联轴器等)的振动特征提取效果不佳[6]。杜名喆等[7]、Hu Mantang 等[8]基于经验小波分解和卷积神经网络方法,分别建立了联轴器和液压泵的智能诊断模型,但该模型所需数据量大,效率低。以上方法为提取液压泵站状态识别特征量提供了有力借鉴,但都仅研究了液压泵站自身工作状态下的振动特征。目前仍缺少对液压泵站振动状态与千米定向钻机动作类型二者关联性的研究,导致无法有效识别钻机的具体动作类型。针对该问题,本文提出了一种基于经验小波变换(Empirical Wavelet Transform,EWT)和模糊C均值(Fuzzy C-means,FCM)聚类算法的矿用千米定向钻机动作识别方法,对5种不同动作下千米定向钻机液压泵站的振动数据进行处理与分析,利用EWT提取出表征动作类型的特征量,利用FCM聚类算法获得隶属度矩阵,实现对千米定向钻机5种动作类型的智能识别。
1 理论基础
1.1 EWT
信号特征提取的关键是运用合适的分解算法对信号进行有效分解。EWT是一种基于频域构建自适应小波的工具,能够从目标信号中提取具有紧支撑傅里叶频谱的调幅-调频分量,并通过检测每个分量自适应地构建经验小波来分解信号。EWT分解克服了经验模态分解及集合经验模态分解模态混叠、复杂程度高和计算量大等问题,更适合于复杂非平稳信号的分解[8]。
EWT分解包括2个步骤:① 将原始信号傅里叶频谱进行自适应分割,得到若干个连续区间。② 构建正交小波滤波器组,提取每个分割区间的模态分量,即经验小波函数(Empirical Wavelet Function,EWF)分量[9]。
EWT能快速提取出富含工况信息的特征量,且具备计算复杂度低、计算量小的特点[10]。本文利用EWT在千米定向钻机执行不同动作时快速分析和处理液压泵站不同测振点的多组振动信号,及时提取表征液压泵站运行状态及对应钻机动作信息的振动特征量样本。
1.2 FCM聚类算法
在通过EWT分解和提取特征量后,为了实现对特定动作类型的识别,需要对特征量准确地进行分类。传统分类方法往往需要大量的训练样本,但实际中并不总是能获得足够多的样本,为减小对样本数量的依赖,可以利用FCM聚类算法进行分类。FCM聚类算法是基于目标函数的一种模糊聚类方法,其核心思想是利用模糊数学聚类分析理论,解决运行状态和事件之间的模糊问题[11]。
FCM聚类算法通过对目标函数的迭代优化达到准确分类的目的,并用隶属度来描述样本与对应类别的相似程度。隶属度越大,两者的相似度就越大。目标函数为
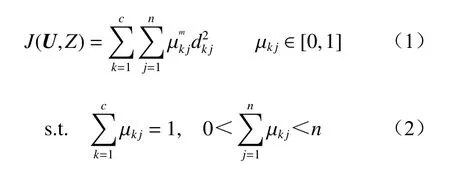
隶属度μkj的计算式为

式中:U为样本集的隶属矩阵;Z为聚类中心;k为类别,k=1,2,…,c,c为类别总数;j为样本,j=1,2,…,n,n为样本长度;μkj为第j个样本属于第k类的隶属度,其值为0~1;m为模糊指数,用来控制模糊程度,m>1,本文取1.5;dkj为第j个样本到第k类聚类中心的欧氏距离;dlj为第j个样本到第l类聚类中心的欧氏距离。
液压泵站每种运行状态下的振动数据都具有一定的聚类结构特点[12],为此,本文利用FCM聚类算法获得隶属度矩阵,将提取的振动特征量样本进行分类和比对,实现自动识别千米定向钻机动作类型的目标。
2 基于EWT和FCM聚类算法的动作识别
基于EWT和FCM聚类算法的矿用千米定向钻机动作识别流程如图1所示。采用EWT求解信号的特征量,利用FCM聚类算法分类结果可靠性强的特点,对千米定向钻机动作类型进行识别。
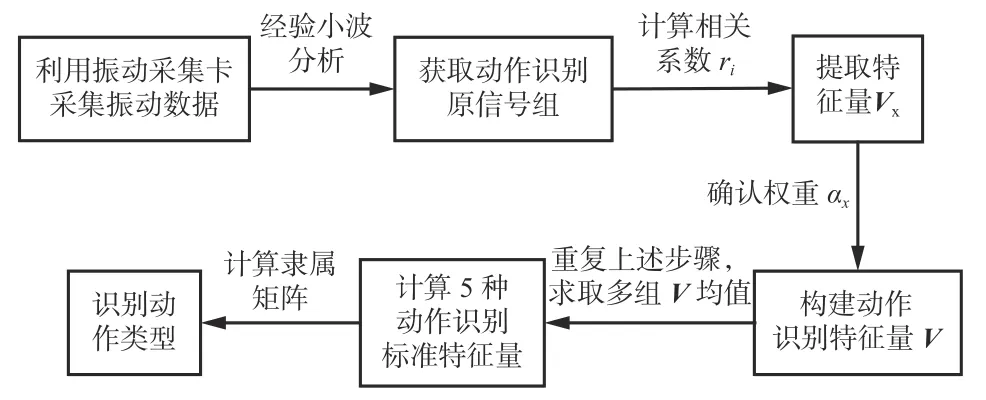
图1 基于EWT和FCM聚类算法的矿用千米定向钻机动作识别流程Fig. 1 Action recognition process of mine directional kilometer drilling rig based on EWT and FCM clustering algorithm
基于EWT和FCM聚类算法的矿用千米定向钻机动作识别具体步骤如下:
(1) 将千米定向钻机的启动和动力头不带钻杆旋转、带钻杆旋转、带钻杆向前慢速钻进、带钻杆向前快速钻进5种动作类型分别记为R1,R2,R3,R4和R5。对5种动作下的振动信息进行经验小波分析,选取p个特征明显的测振点信号作为动作识别原信号组。
(2) 分别对动作识别原信号组进行EWT分解,得到q个EWF分量,分别计算EWF分量与原信号的相关系数ri(i=1,2,…,q)[13]。
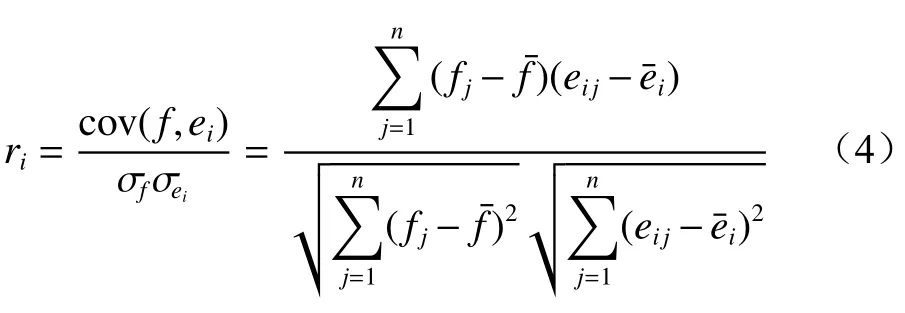
式中:f为原信号;ei为第i个EWF分量;σf和σei分别为原信号和第i个EWF分量的标准差;fj为原信号中第j个元素;和分别为原信号和第i个EWF分量的均值;eij为第i个EWF分量的第j个元素。
由于并非所有的EWF分量都包含丰富的特征信息,结合文献[14]相关系数的选取规则,在ri≥0.3的条件下,选取与原信号相关系数最大的4个EWF分量(如果数量不足,用0填充),从而达到降维和减少计算量的目的[10]。使用平均能量构建每个测振点信号的4维特征量Vx=[v1v2v3v4](x为测振点个数,x=1,2,…,p)。
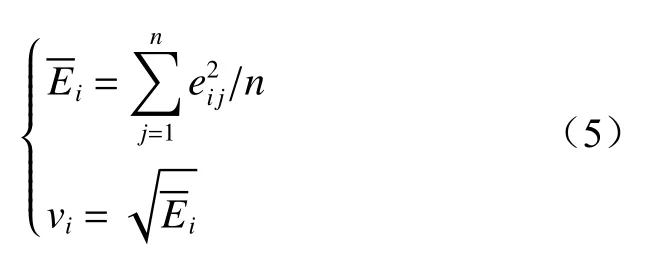
(3) 利用FCM聚类算法研究特征量Vx与千米定向钻机动作类型的关系,构成4×p维动作识别特征量V:
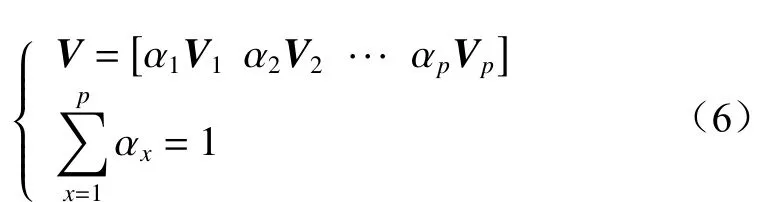
式中αx为权重, αx≥0。
(4) 对多组R1,R2,R3,R4,R5动作的振动信号按上述步骤得到多组动作识别特征量V,计算其平均值,得到5种动作识别标准特征量VR1,VR2,VR3,VR4,VR5。
(5) 计算待识别动作的振动特征量与上述5种动作识别标准特征量之间的隶属度,根据待识别动作的振动特征量与5种动作识别标准特征量之间隶属度的大小,判断千米定向钻机的动作类型。
3 实验验证
3.1 动作原信号组获取
本文以ZYL-17000D型矿用千米定向钻机(图2)为研究对象,对基于EWT和FCM聚类算法的矿用千米定向钻机动作识别方法的可靠性进行实验验证。千米定向钻机的不同动作通过控制液压泵站实现,液压泵站主要由电动机、液压泵和联轴器组成,这3处的振动情况能够比较完整地反映出液压泵站的运行状态,即千米定向钻机的动作类型[15-16]。实验采集了ZYL-17000D型矿用千米定向钻机的电动机和液压泵站的液压泵、联轴器的轴向、水平径向、垂直径向等方向在5种动作下的振动数据,振动方向编号见表1。实验所用采集仪为DEWESoft Sirius,采样频率为10 kHz ,每组数据采样时间为0.25 s。所用振动传感器为Kistler 8692C10三轴加速度传感器,分别安装在电动机、液压泵(远离支撑点位置)和联轴器顶部,x,y,z方向分别对应轴向、水平径向和垂直径向。5种动作下的典型振动数据如图3所示。

图2 ZYL-17000D型矿用千米定向钻机Fig. 2 ZYL-17000D mine kilometer directional drilling rig
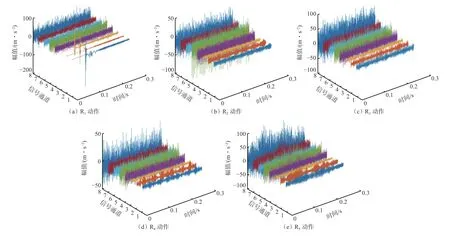
图3 5种动作下8路振动原信号Fig. 3 Eight channels original vibration signals under five actions
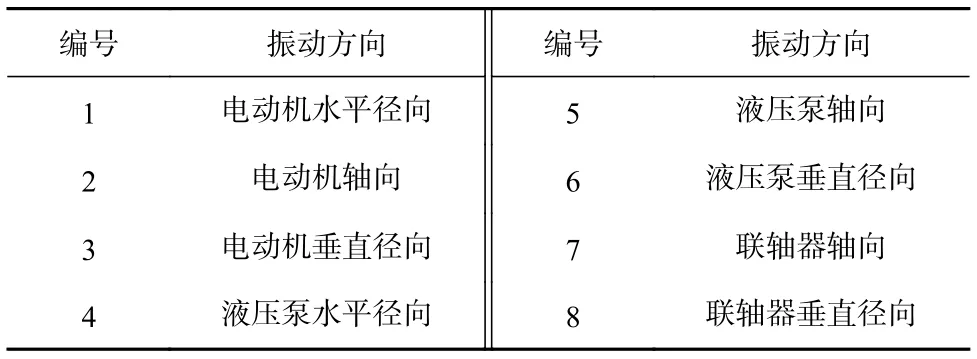
表1 振动方向编号Table 1 Label of vibration direction
3.2 EWT分析波形
将获取的动作原信号组进行EWT分解得到8个EWF分量,并提取相应的振动特征量。5种动作下电动机轴向振动信号经EWT分解的频谱如图4所示。可看出相邻2个EWF分量的频带没有出现交叉,即没有出现模态混叠现象,且EWF分量在各自频带上的幅值有差异;ei幅值与振动能量成正比,幅值越大,电动机轴向信号在该频段的振动加速度越大,相应的振动能量越大,特征越明显。在执行R1动作时,e1和e2幅值相对较大,特征显著;在执行R2动作时,e4和e5特征比较显著,且e4幅值最大;在执行R3动作时,e2,e3,e4,e7特征比较显著;在执行R4动作时,e4和e5特征比较显著,且e5幅值比e4略大;在执行R5动作时,e4特征最显著。由此可以得出,钻机执行不同动作时,EWF分量ei幅值分布情况呈现不同特征,提取的特征量也不同,所以,根据提取的特征量在不同动作下的差异性可实现对动作类型的区分。
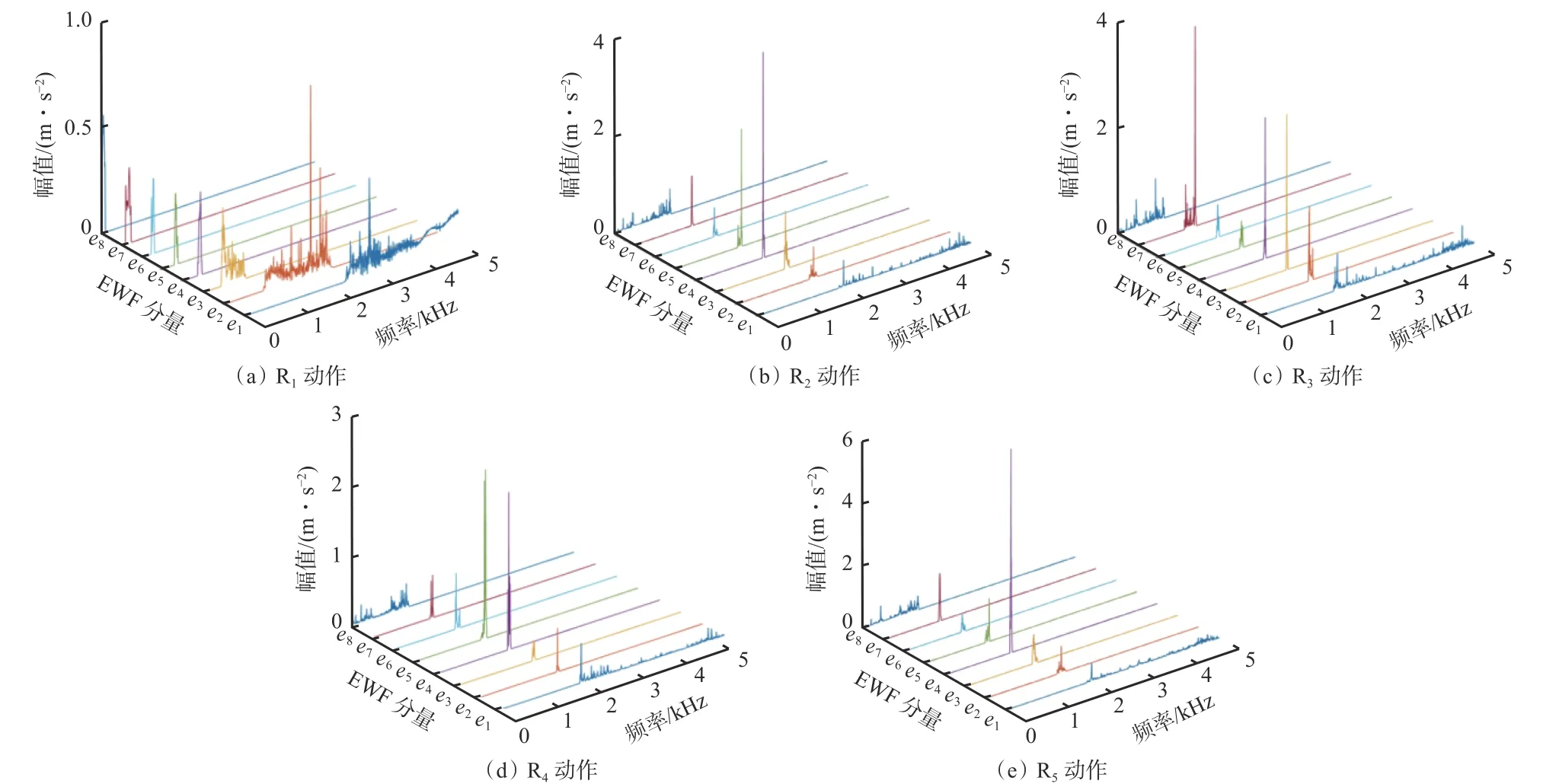
图4 5种动作下电动机轴向振动信号的EWF各分量频谱Fig. 4 Spectrum of EWF components of motor axial vibration signal under five actions
从电动机轴向振动信号的EWT时频谱(图5)中可更直观地分析执行5种不同动作时振动信号所包含的频率和瞬时能量等特征信息。从图5可看出,在执行R1动作时,振动能量主要集中在电动机启动瞬间(约0.06 s时);在执行R2动作时,Hilbert谱在1 kHz处分布不均且有间断,而在1.3 kHz和1.55 kHz处分布明显且连续,振动能量主要集中在1.5~1.6 kHz频段;在执行R3动作时,Hilbert谱在1.3 kHz和1.6 kHz处分布明显,且振动能量集中在1.55~1.65 kHz频段内;在执行R4动作时,Hilbert谱在1.55 kHz处分布明显,但不连续,在0.12 s和0.2 s左右处有间断,且振动能量主要集中在1.55 kHz左右;在执行R5动作时,Hilbert谱在1.3 kHz处分布明显且连续,而在1.55 kHz处分布明显,但不连续,在0.05 s左右处有间断,振动能量主要集中在1.55 kHz左右。
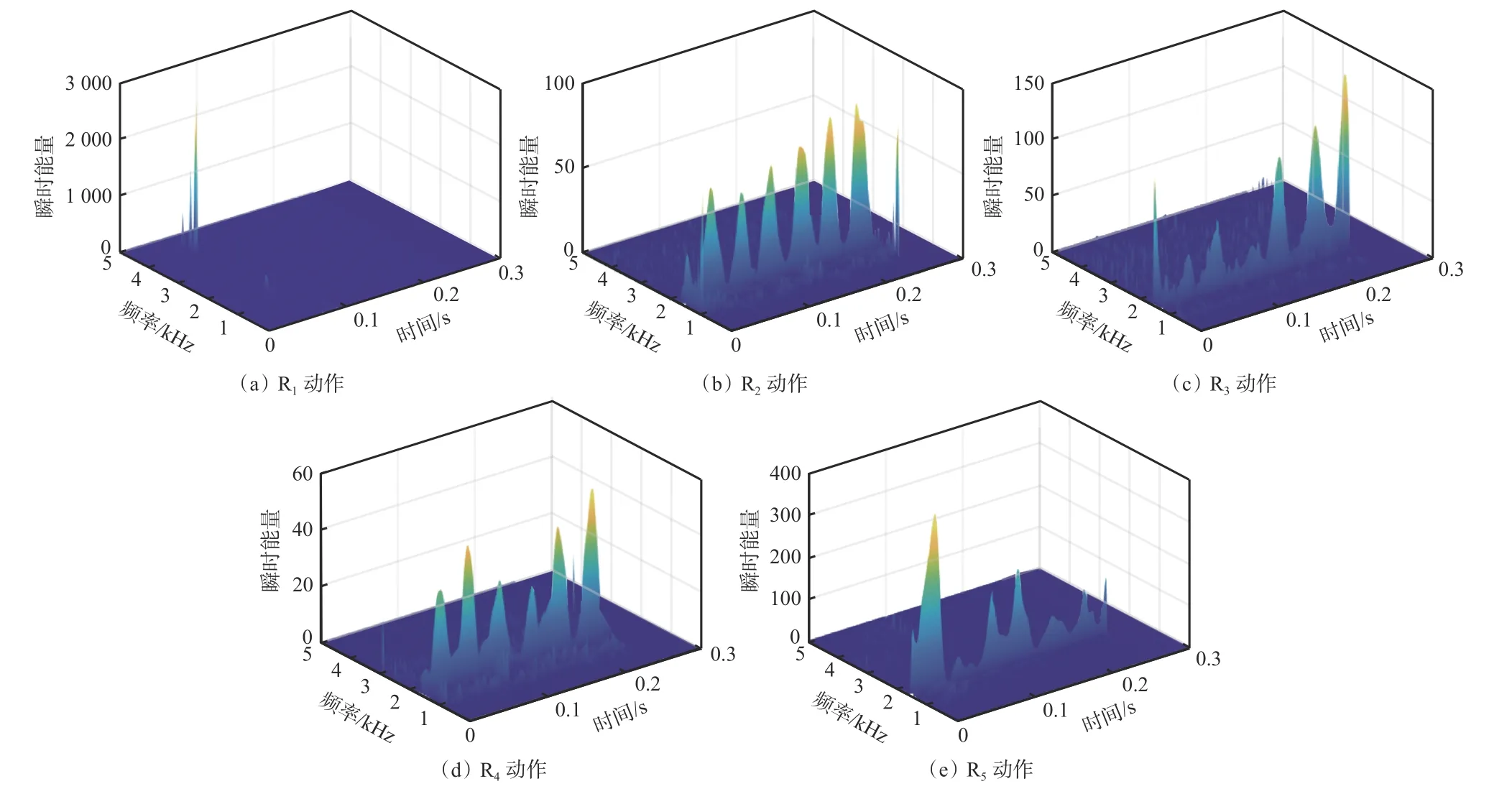
图5 电动机轴向振动信号EWT时频谱Fig. 5 The EWT time-frequency spectrum of the motor axial vibration signal
3.3 动作识别标准特征量构建
除R1动作外,其他4种动作下电动机轴向振动信号能量主要分布频带非常接近,提取的特征量差异较小,会降低千米定向钻机动作类型的识别精度,所以需要结合液压泵和联轴器振动信号进行综合分析判别。经过对8组振动信号的时频能量进行分析,分别选取电动机、液压泵和联轴器振动能量分布较为明显的方向上的信号(即表1中编号为2,5,8对应的信号)作为动作识别原信号组,用来构建动作识别特征量。
针对5种动作各选取10组振动数据,每组数据样本长度均为5 000,提取电动机轴向、液压泵轴向和联轴器垂直径向振动信号的特征量,分别记为V1,V2,V3,见表2。可看出相同动作下,特征量相似;而不同动作下,特征量差别较大, 可通过提取的特征量识别动作。
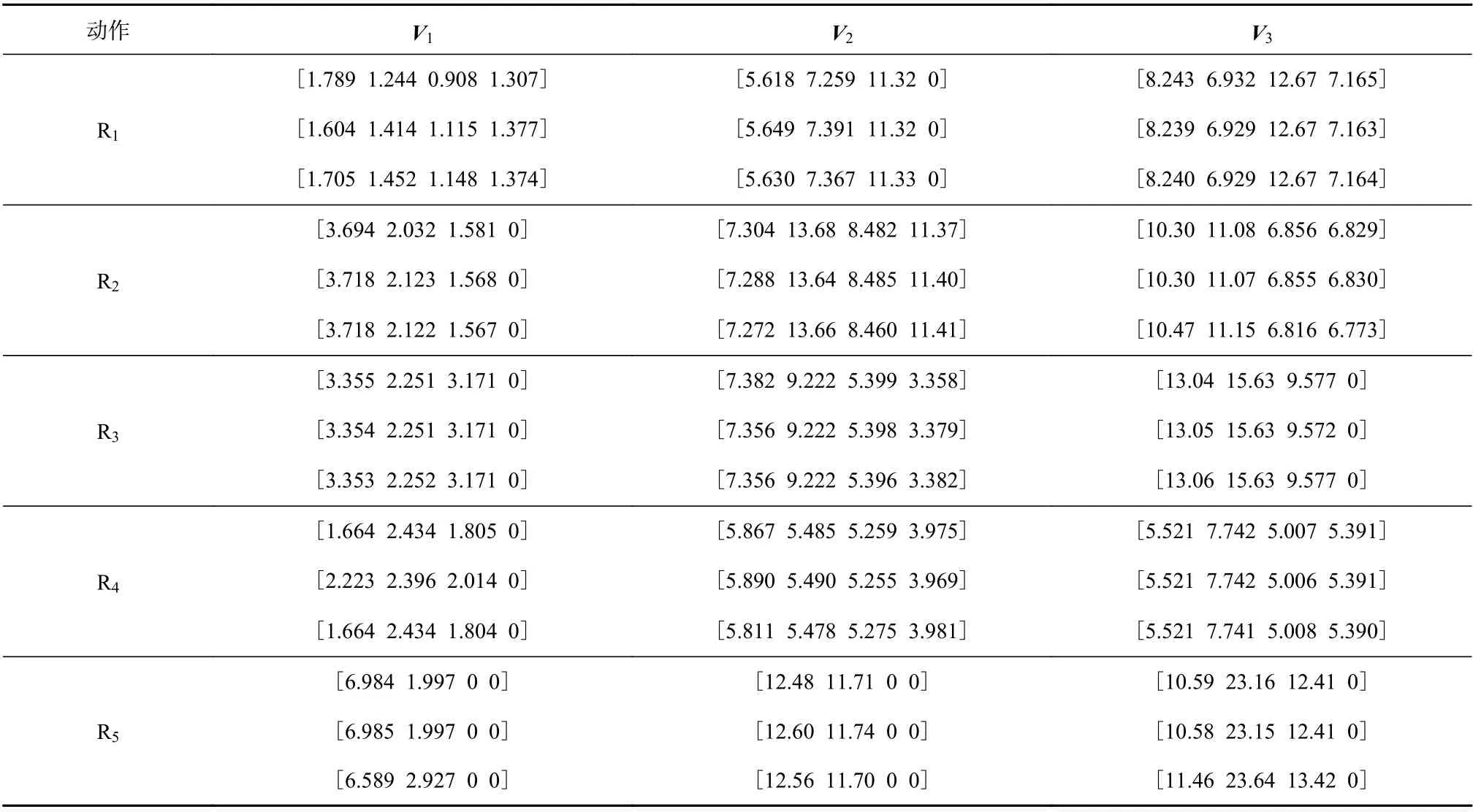
表2 5种动作识别原信号组的特征量Table 2 Eigenvectors of the original signal group for action recognition under five working conditions
由特征量构建动作识别特征量V =[α1V1α2V2α3V3],应 用FCM聚 类 算 法,改 变 权 重α1,α2,α3取值,获得一系列不同动作下的特征量聚类效果图,选择聚类效果最佳的一组权重构建动作识别特征量。在千米定向钻机工作时,动力头带动钻杆旋转,而液压泵的位置距离动力头最近,因此液压泵轴向信号更有利于表征千米定向钻机的动作信息,则α2占比应相对较大。
当α1=1,α2=α3=0时,5种动作识别特征量聚类结果如图6(a)所示,可看出聚类性能较差,R1和R4、R4和R5动作间有交叉混叠现象出现,而且在执行R3,R4,R5动作时有3组数据识别错误。当α1=α3=0,α2=1时,5种动作识别特征量聚类结果如图6(b)所示,可看出钻机执行5种动作时的振动特征量被完全区分开,而且类内聚合度高,聚类性能较好。当α1=α2=0,α3=1时,5种动作的识别特征量聚类结果如图6(c)所示,可看出虽然振动特征量被区分开,但在执行R2动作时,数据比较分散,类内聚合度较低,聚类性能一般。
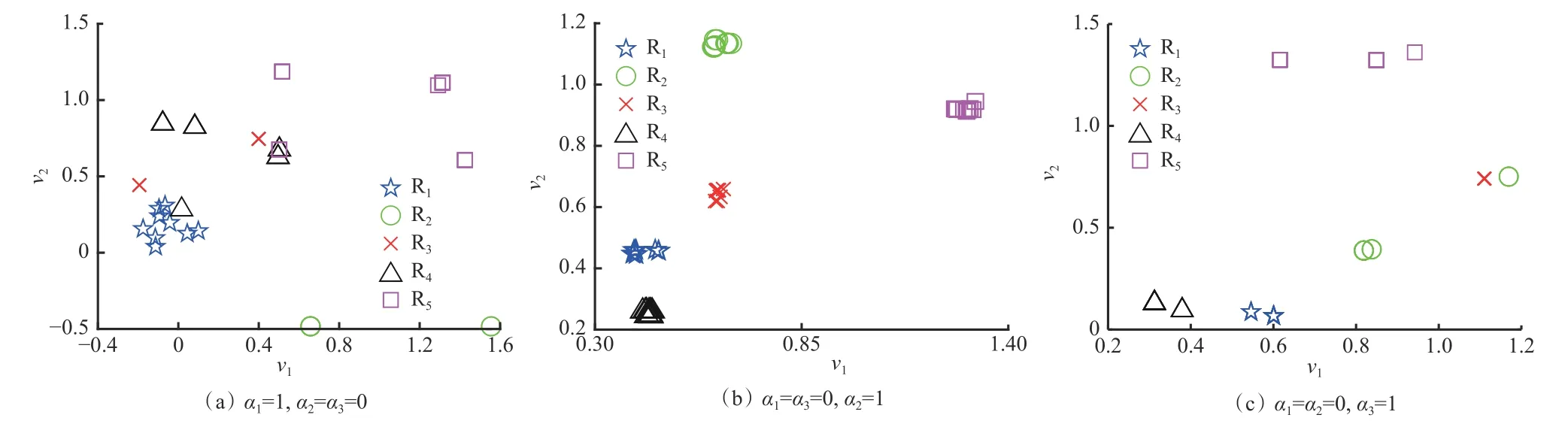
图6 不同权重下动作识别特征量聚类结果Fig. 6 Clustering results of action recognition characteristic quantities under different weights
在分别执行5种动作时,液压泵轴向振动信号特征量的聚类效果最显著。当选取α1=α3=0,α2=1,以液压泵轴向振动特征量作为动作识别特征量时,识别效果最佳,结论与分析结果相符。
分别求取5种动作下各10组V2的平均值,得到动作识别标准特征量依次为VR1=[5.786 7.317 11.32 0],VR2=[7.416 13.75 8.44 11.32],VR3=[7.375 9.135 5.390 3.384],VR4=[5.897 5.431 5.295 3.954],VR5=[12.51 11.74 0 0]。
3.4 动作类型识别
分别选取千米定向钻机5种动作下各25组振动数据,即125组数据作为测试样本,利用FCM聚类算法计算待识别动作的振动特征量与状态识别标准特征量之间的隶属度,隶属度越大,表明该待测样本属于对应动作的概率越大。分别列举5种动作下前2组样本,共计10组样本的隶属度,见表3。其中,加粗部分为测试样本判定动作与样本实际动作之间的隶属度。从表3可看出,样本的特征量与对应的动作识别特征量的隶属度远大于与其他动作识别特征量的隶属度,且隶属度均大于0.98,判别结果与钻机实际动作类型一致。125组测试样本中仅有4组测试样本的隶属度较低,依次为0.619,0.684,0.602,0.667。经分析,这4组测试样本属于R1动作,由于R1动作时间短,在采集R1动作信号时,采集了一部分R2动作信号,使得这4组测试样本与R2动作的隶属度达到了0.3以上,最终导致这4组测试样本与R1动作的隶属度较小。实验结果表明,本文所述方法在隶属度大于0.9的条件下判别准确率达96.8%。
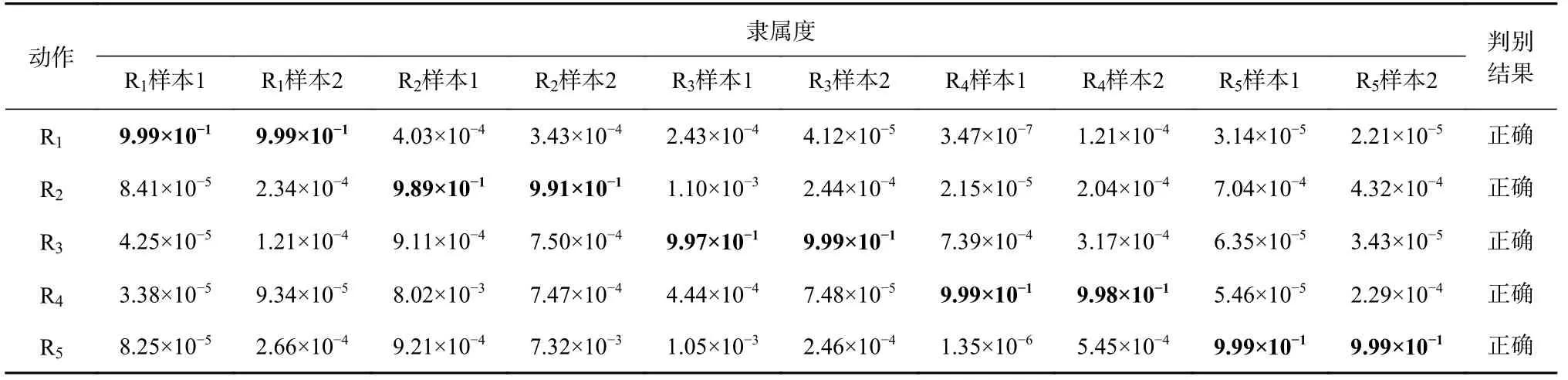
表3 10组测试样本的隶属度Table 3 Membership degree of test samples (group 1-10)
4 结论
(1) 千米定向钻机执行不同动作时,其电动机、液压泵和联轴器振动信息的经验小波函数可体现出不同的特征。
(2) EWT时频谱图表明,电动机轴向、液压泵轴向和联轴器垂直径向振动信号可作为千米定向钻机动作识别原信号组,其中液压泵轴向的振动信号表征千米定向钻机动作类型的效果最佳。
(3) 利用FCM聚类算法对提取的千米定向钻机动作类型特征量进行识别,结果表明:在待识别动作与标准识别特征量之间的隶属度大于0.9的条件下,识别准确率达96.8%,验证了基于EWT和FCM聚类算法的千米定向钻机动作识别方法的准确性,为实现远程监测千米定向钻机运行状态提供了技术支持。
(4) 该方法利用加载试验台模拟千米定向钻机运行负载,与实际工况存在一定的差距。因此,下一阶段的研究工作是进行现场试验,以进一步提高千米定向钻机动作识别方法的有效性和准确性。
