基于正交试验的钢丝绳探伤仪结构参数优化

田劼，孙钢钢，李睿峰，王伟

（1. 中国矿业大学（北京） 机电与信息工程学院，北京 100083；2. 中国矿业大学（北京） 煤矿智能化与机器人创新应用应急管理部重点实验室，北京 100083）

0 引言

钢丝绳由于具有强度高、弯曲性能好、运动平稳、不易整根骤断、承受动载和过载能力强及在高速工作条件下运行和卷绕无噪声等优点，被广泛应用于矿山、石油钻井、冶金、建筑、交通、港口、军工等多个领域[1]。矿井提升机是联系井下与地面的主要运输设备，担负提升煤炭和矸石、下放材料、升降人员和设备的重要任务。钢丝绳是矿井提升机的主要组成构件，被称为提升机的“生命线”，但由于钢丝绳工作环境恶劣、工作状况复杂，在运行中易出现金属截面损失和局部损伤，如断丝、磨损、锈蚀等[2-3]，因此，对钢丝绳运行状态进行检测至关重要。现有钢丝绳无损检测方法有固体声测法、光学法、声学检测法、电磁检测法、X-射线法、磁致伸缩法、电涡流法、电流法、振动法及图像识别等[4-5]，应用最多的是图像视觉[6]和基于电磁的无损检测法[7]，基于电磁的钢丝绳探伤仪是最可靠的检测方式[8]。基于电磁的钢丝绳探伤仪作为钢丝绳无损检测的重要设备，可以准确检测钢丝绳的在役状况，大幅提高钢丝绳的使用周期。

在钢丝绳损伤检测中，探伤仪结构设计对钢丝绳损伤检测精度至关重要。为了设计一种体积小、质量小且励磁能力强的钢丝绳探伤仪，通常需对其结构参数进行分析。但是，大多数学者仅对单个结构参数做了分析，仅对单因素不同条件下的数据进行了试验探究并得出一组基于该单因素下的数据结论[9-10]。但钢丝绳探伤仪检测精度受多方面因素的影响，单因素研究仅是针对其他因素不变的情况下该因素的影响规律，使得不同因素的变化也会产生相同的效果，不利于钢丝绳探伤仪的轻量化设计[11-12]。针对以上问题，本文提出了一种基于正交试验的钢丝绳探伤仪结构参数优化方法[13]，并对影响钢丝绳探伤仪的各参数进行显著性分析，对同因素下不同水平之间的影响效果进行了多种分析，得出了影响钢丝绳探伤仪检测精度的几个重要结构参数，并依此优化探伤仪结构，提升其检测性能。

1 钢丝绳探伤仪结构参数对检测精度的影响

钢丝绳由铁磁性材料制成，其磁探伤原理如图1所示。钢丝绳探伤仪主要由衔铁、磁铁、检测元件等组成。磁铁磁化钢丝绳，并与衔铁、钢丝绳、空气形成励磁回路，当钢丝绳存在缺陷时，缺陷周围的磁感应强度值会发生变化，通过检测元件测得钢丝绳缺陷周围的磁感应强度变化量，可判断钢丝绳损伤状况[14]。

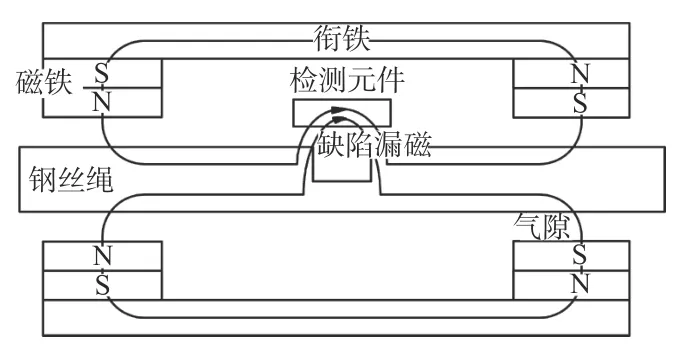
图1 钢丝绳探伤原理Fig. 1 Wire rope flaw detection principle

单个和组合径向环形磁铁励磁环结构简图如图2所示。环形磁铁励磁环的磁化方向沿磁环半径向内或向外。

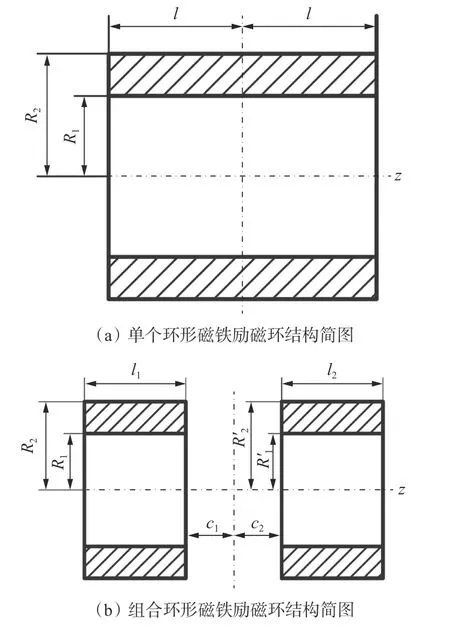
图2 单个和组合磁铁励磁环结构简图Fig. 2 The structure of single and combined permanent magnet excitation ring

由毕奥-萨伐尔定律可得单个环形励磁磁铁轴线磁场强度表达式[15]：

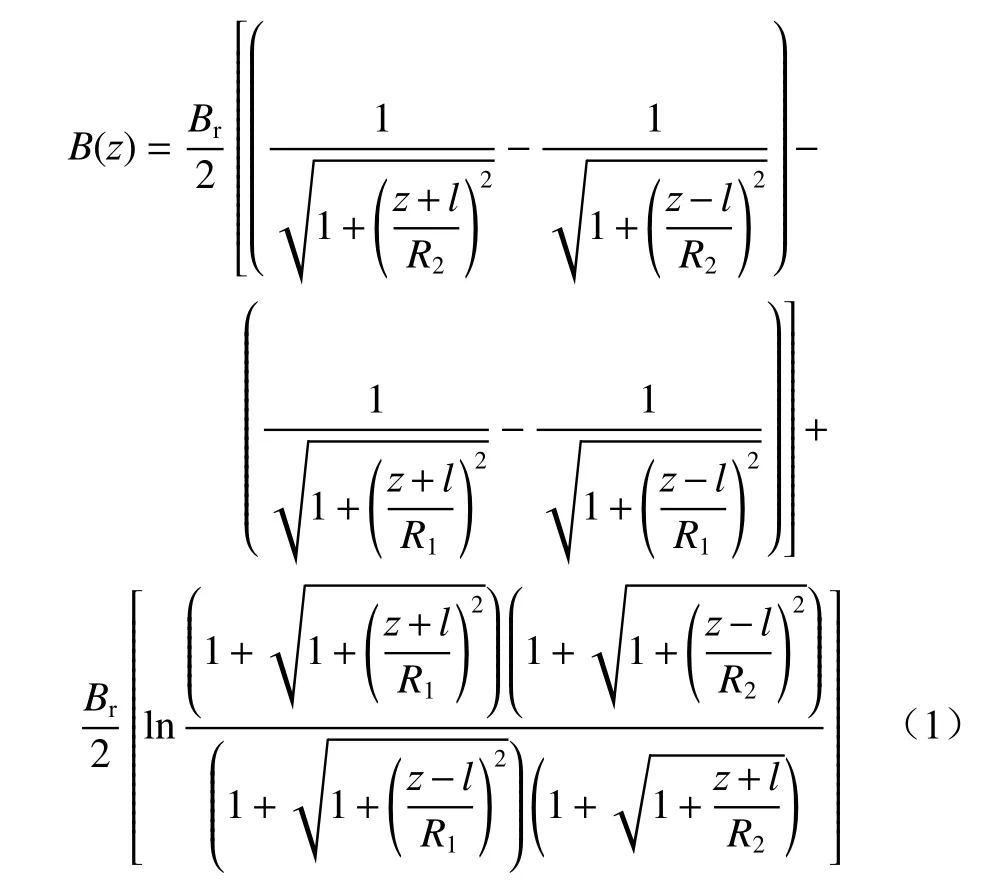
式中：B(z)为轴线上的磁感应强度，z为磁环中轴线坐标，左正右负；Br为剩磁；l为1/2场磁环长度；R2为单个磁环外半径；R1为单个磁环内半径。

一副环形组合磁铁轴线磁感应强度表达式为

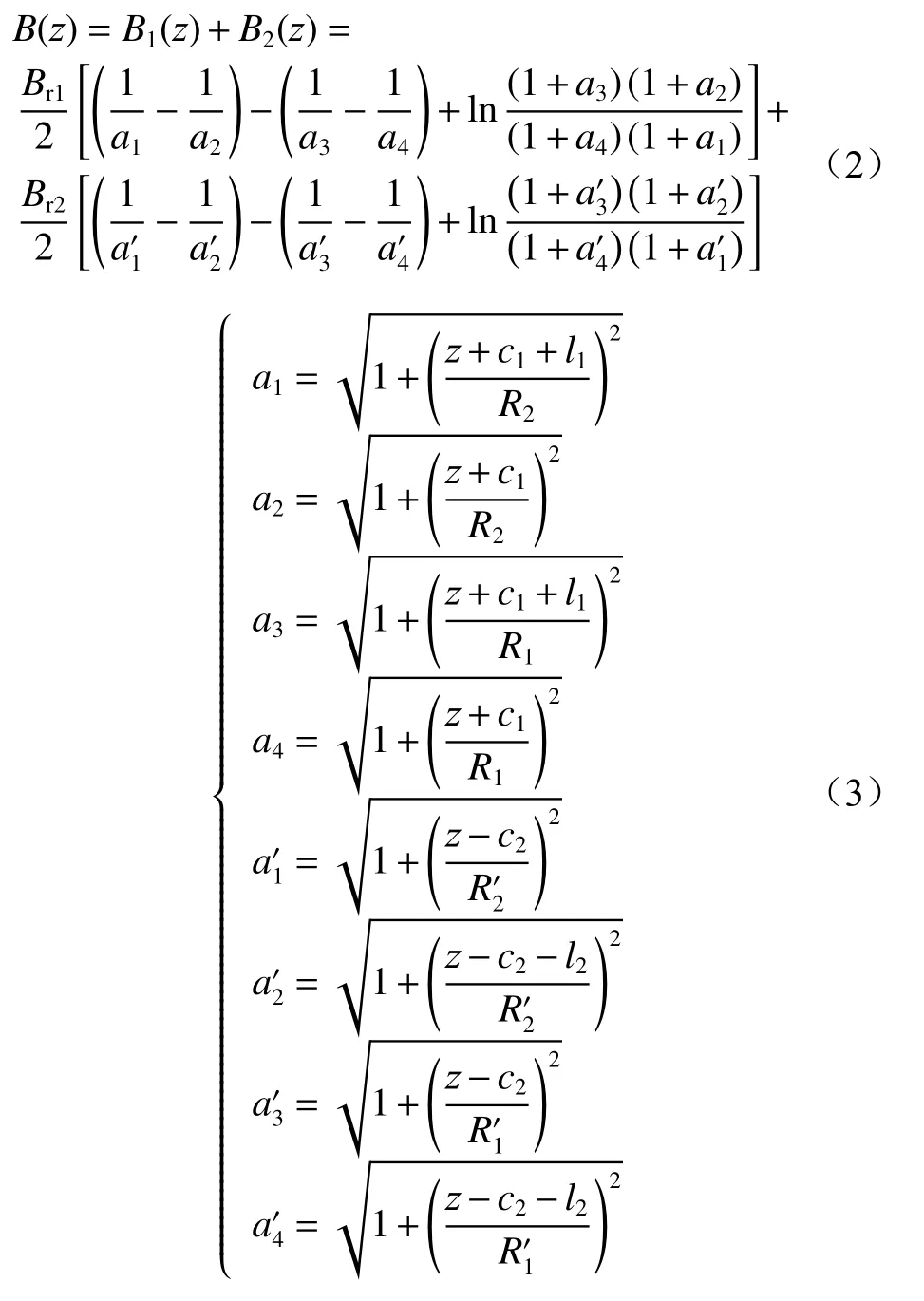
式中：B1(z)，B2(z)为组合磁环的两磁环在z位置产生的磁感应强度；Br1和Br2为组合磁环的两磁环的剩磁；a1-a4，a′1-a′4为中间变量；c1，c2为组合磁环靠近原点坐标一端距离原点组合的长度；l1，l2为组合磁环单个磁环的全长；R2′为组合磁环中另一个磁环的外半径；R1′为组合磁环中另一个磁环的内半径。

依据磁环的磁场理论分析，由式（2）和式（3）可得影响磁环磁场分布的关键参数主要有磁环的厚度和长度及两磁环之间的距离（衔铁的长度）。

为进一步探究钢丝绳探伤仪结构参数对检测精度的影响，将图1所示的检测原理根据磁路定理等效简化为如图3所示的模型[16]。

图3 钢丝绳探伤仪等效电路模型Fig. 3 Equivalent circuit model of wire rope flaw detector

基于磁路欧姆定律和磁路基尔霍夫定律可知

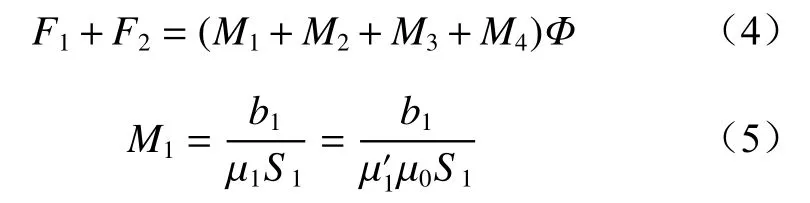
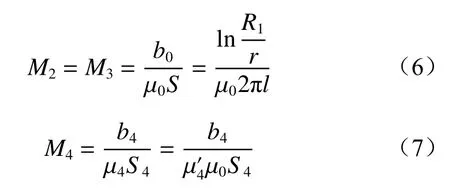
式中：F1，F2为磁铁的磁势；M1为钢丝绳磁阻；M2和M3为钢丝绳与磁环间空气的磁阻；M4为两磁环间衔铁的磁阻；Φ为磁路磁通；b1为钢丝绳磁路中的有效长度；μ1为钢丝绳磁导率；S1为钢丝绳等效截面积；μ′1为钢丝绳相对磁导率；μ0为空气磁导率；b0为磁环与钢丝绳间气隙磁路的等效平均长度；S为磁环与钢丝绳间气隙磁路的等效截面积；r为钢丝绳等效半径；b4为衔铁所在磁路中的有效长度；μ4为衔铁磁导率；S4为衔铁等效截面积；μ′4为衔铁相对磁导率。

将式（5）-式（7）代入式（4）可得

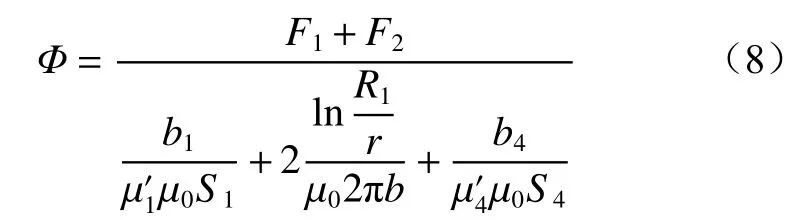
式中b为磁铁磁环的长度，即磁路中气隙的长度。

综上可得，影响钢丝绳探伤仪检测精度的结构参数有衔铁的结构参数（长度、截面积）、气隙的结构参数（气隙的宽度、气隙的长度）及磁环理论结构中的永磁环的参数等。

2 基于正交试验的钢丝绳探伤仪结构参数优化分析

2.1 正交设计及试验

影响钢丝绳探伤仪励磁效果从而影响最终检测精度的因素有很多，本文结合钢丝绳探伤仪的实际工况，选取磁铁长度Lc、磁铁厚度Hc、衔铁厚度Hx、衔铁长度Lx（或者两磁铁的距离）和倒角参数C为主要可变参数对钢丝绳探伤仪进行变量化的正交试验研究，各参数如图4所示。要获得最优的钢丝绳探伤仪结构参数，就要对以上5组因素的影响进行具体分析。若每组因素都有5个水平，就要进行55=3 125组试验，需耗费巨大的人力物力资源。正交试验是研究多因素多水平的一种试验方法，根据正交性从全面试验中挑选出部分有代表性的点进行试验，这些有代表性的点具备了“均匀分散，齐整可比”的特点，是一种高效、快速、经济的试验设计方法。

图4 钢丝绳探伤仪结构参数Fig. 4 Structure parameters of wire rope flaw detector

基于正交表进行各因素参数的设置后，需要对组合水平的结果进行评价。钢丝绳探伤仪所检测到的钢丝绳损伤信号为漏磁电信号，漏磁电信号是依靠霍尔元件感应漏磁场的变化转换而来，因此选用损伤处漏磁强度的大小作为试验的评价结果。由于结构参数的变化，使得钢丝绳探伤仪的磁路发生变化，从而使最终的损伤处的漏磁强度发生变化，针对该问题，本文调整评价指标，将最终评价指标定为有损伤和无损伤之间的漏磁差值。

在以上5组因素上添加1组空白列O作为误差因素，以便进行误差分析。按正交表L25(56)安排试验，只需要进行25组试验，从而大大减少了工作量。依据经验，选取常见的主要水平得出表1的因素水平分布情况。依据正交表进行试验的结果见表2。

表1 正交试验的因素水平情况Table 1 Factors level of orthogonal test

2.2 极差分析

极差分析方法是利用数理统计方法计算出正交表中每列的极差值Δ，根据水平均值和每个因素的极差值可求得最佳水平组合和影响因素的主次顺序。某个因素的极差定义为该因素的最大水平均值与最小水平均值之差，极差大，表明该因素的影响大，是主要因素；极差小，表明该因素的影响小，为次要因素。

进行极差分析时，首先计算每个因素中具体水平值的总值Tij，它等于第i个 因素中第j个水平值所做所有实验结果之和；然后计算水平均值；最后可计算得到每个因素的极差值Δij。和 Δij计算公式如下:

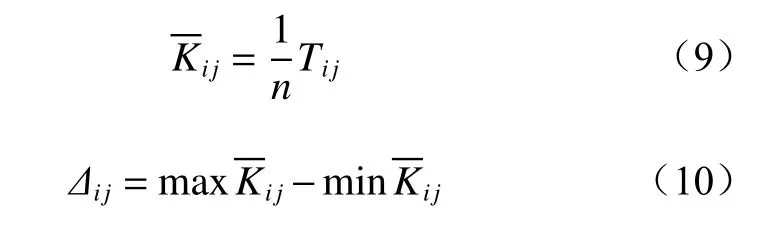
式中n为水平j出现的次数。

通过式（9）和式（10）可求出该因素的极差值。根据表2中的损伤程度数据，对钢丝绳探伤仪结构的各个参数进行极差分析计算，结果见表3。

表2 参数水平组合正交表及损伤程度结果Table 2 Parameter level combination orthogonal table and damage degree results

由表3计算出的极差值可知，磁铁长度Lc、磁铁厚度Hc、衔铁厚度Hx、衔铁长度Lx、倒角C和空白列O这6个因素极差值按从大到小的排序为Hc＞Lc＞Lx＞Hx＞O＞C，即对钢丝绳探伤仪结构产生影响的6个因素中，磁铁厚度Hc所对应的极差值最大，其对钢丝绳探伤仪检测精度的影响最大；其次为磁铁长度Lc、衔铁长度Lx。而在仿真过程中，虽然对钢丝绳探伤仪的实际工作环境做过充分的模拟，但仍有其他因素干扰仿真结果，本文中加入的空白列也是对其他误差因素的一种考虑。试验结果表明空白列的极差值大于倒角因素，说明可能存在其他因素的影响比倒角因素的影响更大，实际中可忽略不计。

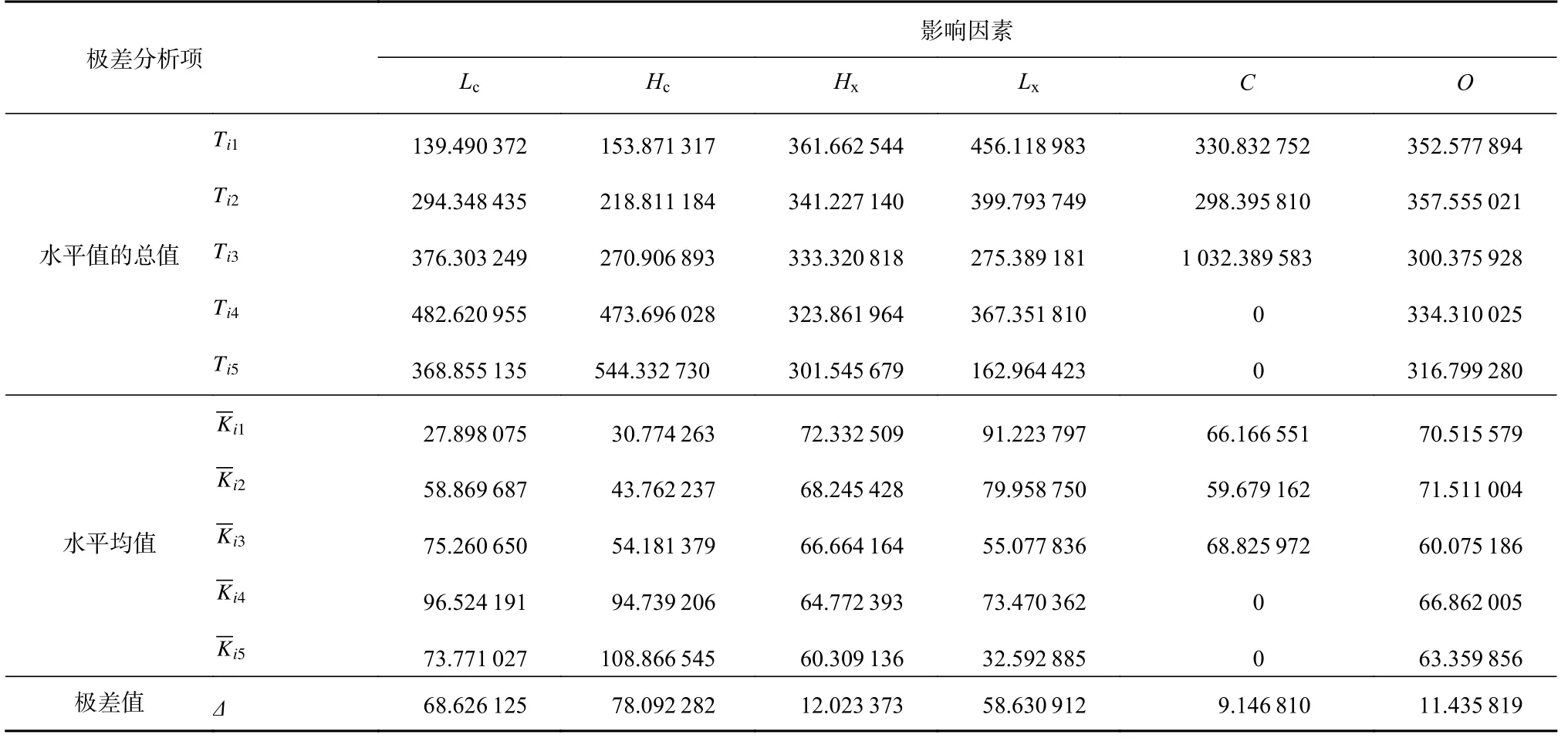
表3 影响钢丝绳探伤仪检测精度的因素极差分析Table 3 Range analysis of factors affecting detection precision of wire rope detector

各因素的水平变化如图5所示，可看出在多因素水平的共同参与下，磁铁厚度Hc对于损伤程度的影响整体呈正相关关系，即随着磁铁厚度Hc的增大，检测精度会明显提升；磁铁长度Lc在70 mm以下呈正相关关系，检测精度随磁铁长度Lc增加而明显提升；衔铁厚度Hx对于损伤程度的影响呈负相关关系，精度的变化不明显；衔铁长度Lx对于损伤程度的影响整体呈负相关关系，长度越长，检测精度越差；倒圆角的效果最好，倒直角效果最差。

图5 损伤程度随各水平的变化趋势Fig. 5 Change trends of damage degree with different levels

2.3 方差分析

极差分析方法只能得出各因素对损伤程度影响的相对大小，不能确定每个因素对损伤程度的影响是否显著及显著性的大小，而方差分析可通过分析试验数据，研究因素对损伤结果的影响是否显著。因此，通过对钢丝绳探伤仪结构的各参数数据进行方差分析，可探究磁铁长度Lc、磁铁厚度Hc、衔铁厚度Hx、衔铁长度Lx、倒角C和空白列O这6个因素对钢丝绳探伤仪所产生影响的显著性，根据显著性结果可以有针对性地控制该因素相关参数的水平，从而在钢丝绳探伤仪的设计过程中选择性的控制这些结构参数，达到最优的检测效果。

根据正交试验方差分析理论及表2中在各个因素水平下的钢丝绳损伤数据，可计算出各因素的离差平方和、自由度、均方值和方差比（f值，f值越大，表示越显著），见表4。表中P值是用来判定假设检验的一个参数。由表4可知，在影响钢丝绳探伤仪检测精度的可控5个因素中，磁铁厚度Hc、磁铁长度Lc和衔铁长度Lx对钢丝绳探伤仪的检测精度都有显著性的影响，而倒角C和衔铁厚度Hx相对呈现不显著性（这里取置信水平为95%），尤其是衔铁厚度Hx，其均方值还没有空白列O大，进一步说明了衔铁厚度Hx对钢丝绳探伤仪检测精度的影响很小，设计时可忽略不计。

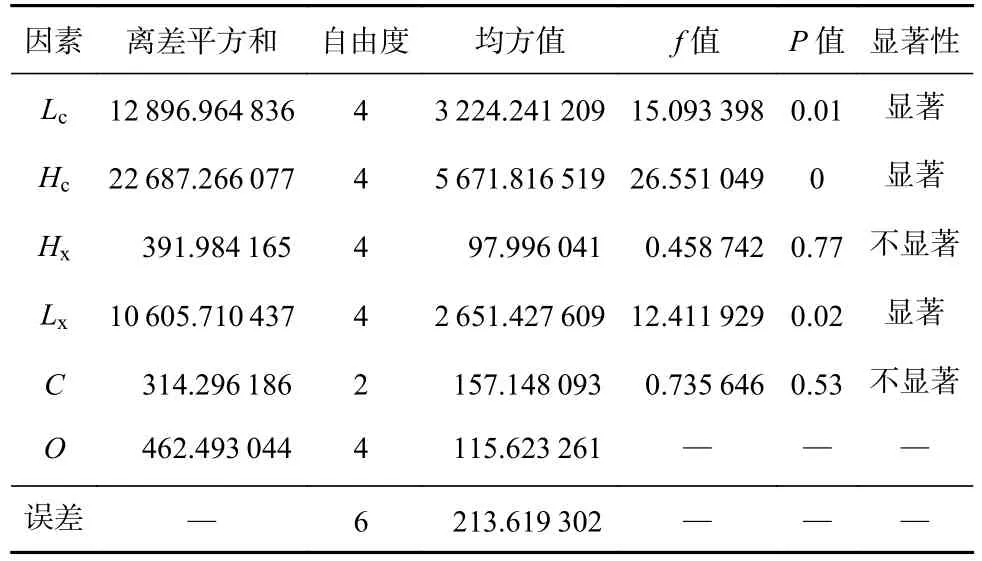
表4 影响钢丝绳探伤仪检测精度因素的方差分析Table 4 Variance analysis of factors affecting detection precision of wire rope detector

3 探伤仪优化效果对比

3.1 优化后探伤仪磁化效果

根据上述分析结果，本文最终确定的钢丝绳探伤仪各参数如下[17-18]：磁铁厚度Hc=30 mm，磁铁长度Lc=70 mm，衔铁长度Lx=180 mm，衔铁厚度Hx=3 mm ，倒角C为倒圆角。

根据以上参数绘制其等效简化模型，并根据等效简化模型，采用Ansoft maxwell分析软件对其检测性能进行研究。采用基于正交试验的优化方法优化后的钢丝绳探伤仪检测损伤钢丝绳时的磁场分布情况如图6所示。可看出经过优化后的钢丝绳探伤仪表现出磁路整齐，其主要磁感应强度集中在钢丝绳和衔铁中部，钢丝绳等效简化模型内部的磁感应强度更是达到了2 T以上，符合钢丝绳励磁效果的最低标准；对于损伤处有明显的磁场泄露情况（图中圈出部分），从而验证了优化后的探伤仪具有检测钢丝绳损伤的效果。

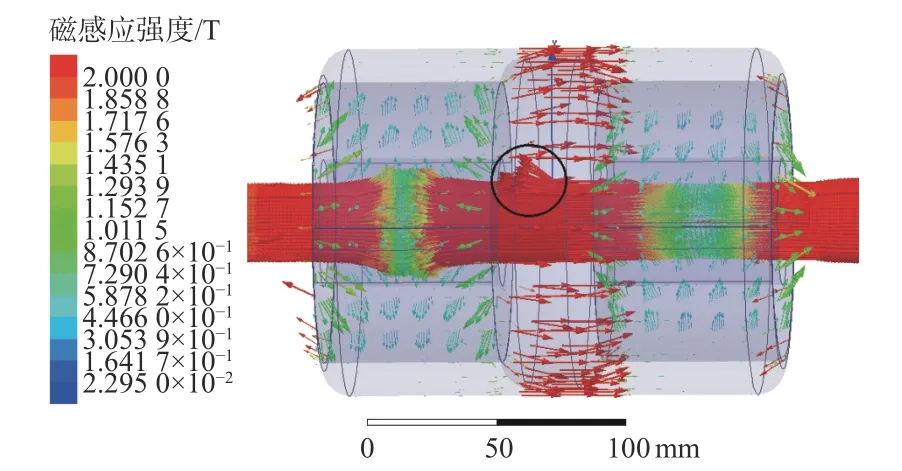
图6 优化后模型磁场分布Fig. 6 Magnetic field distribution of the optimized model

同时，对钢丝绳取提离值为3 mm的位置（损伤位置前后20 mm的距离内）做其周向均布一周的磁感应强度的提取，结果如图7（a）所示，可看出所提取的钢丝绳损伤在圆周上的磁感应强度仅传感器对应的位置（图中0°曲线）有明显的变化，也验证了基于正交试验的优化方法优化后的钢丝绳探伤仪对损伤相位的检测有一定的效果。将其损伤所在位置的8个轴向检测相位[19]所提取的磁感应强度值以雷达图形式绘出（图7（b）），可看出损伤相位的传感器所采集到的磁感应强度与其余位置有明显的差异，验证了优化后的探伤仪对损伤相位检测也具有一定的敏感性。

图7 周向八相位磁感应强度分布及各相位损伤程度分布Fig. 7 Circumferential 8-phase magnetic induction intensity distribution and phase damage distribution

3.2 优化前后探伤仪的对比

将基于正交试验的优化方法优化后的钢丝绳探伤仪与优化前的钢丝绳探伤仪做对比验证，其结果如图8和图9所示。可看出经过基于正交试验的优化方法优化后的钢丝绳探伤仪在磁铁磁性相同的情况下能为钢丝绳提供较高的励磁效果；对于漏磁场来说，相比优化前的钢丝绳探伤仪，优化后的钢丝绳探伤仪不仅在磁感应强度上有大幅度提高，在其空域分布中也有明显的改善，对传感器布置位置（提离值）的要求也相对宽泛，提高了钢丝绳探伤仪本身的检测精度。

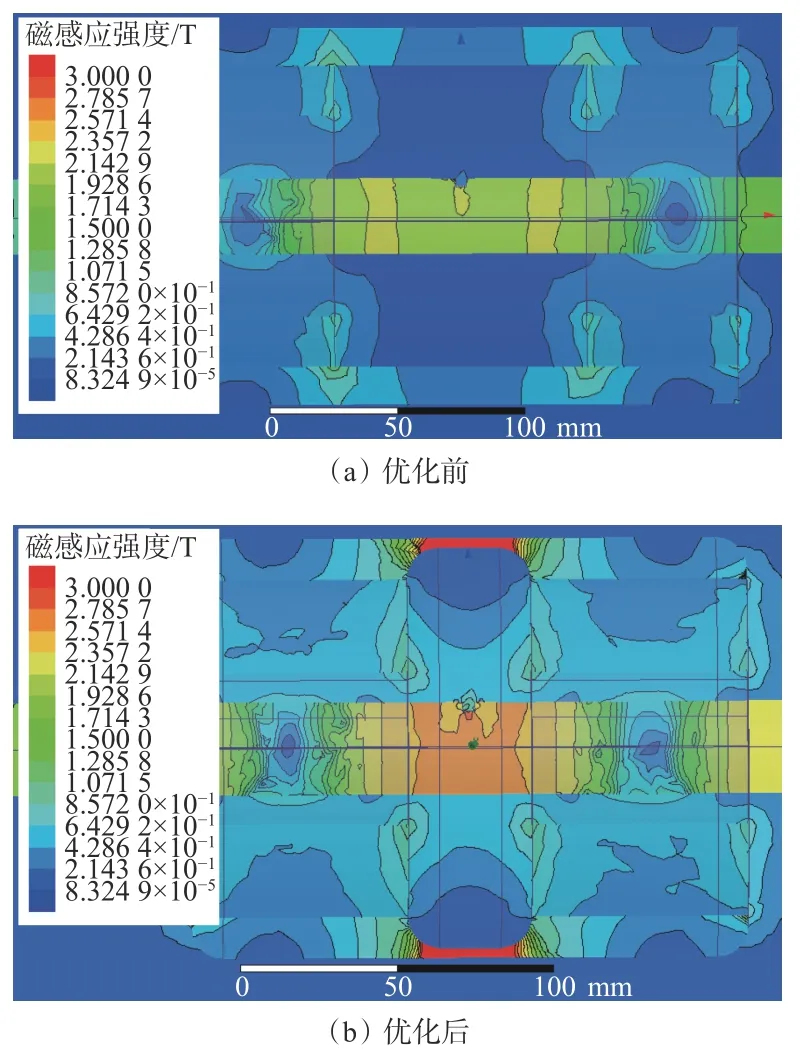
图8 优化前后钢丝绳探伤仪竖直面磁感应强度云图Fig. 8 Magnetic induction intensity cloud chart of vertical plane before and after optimization of wire rope flaw detector

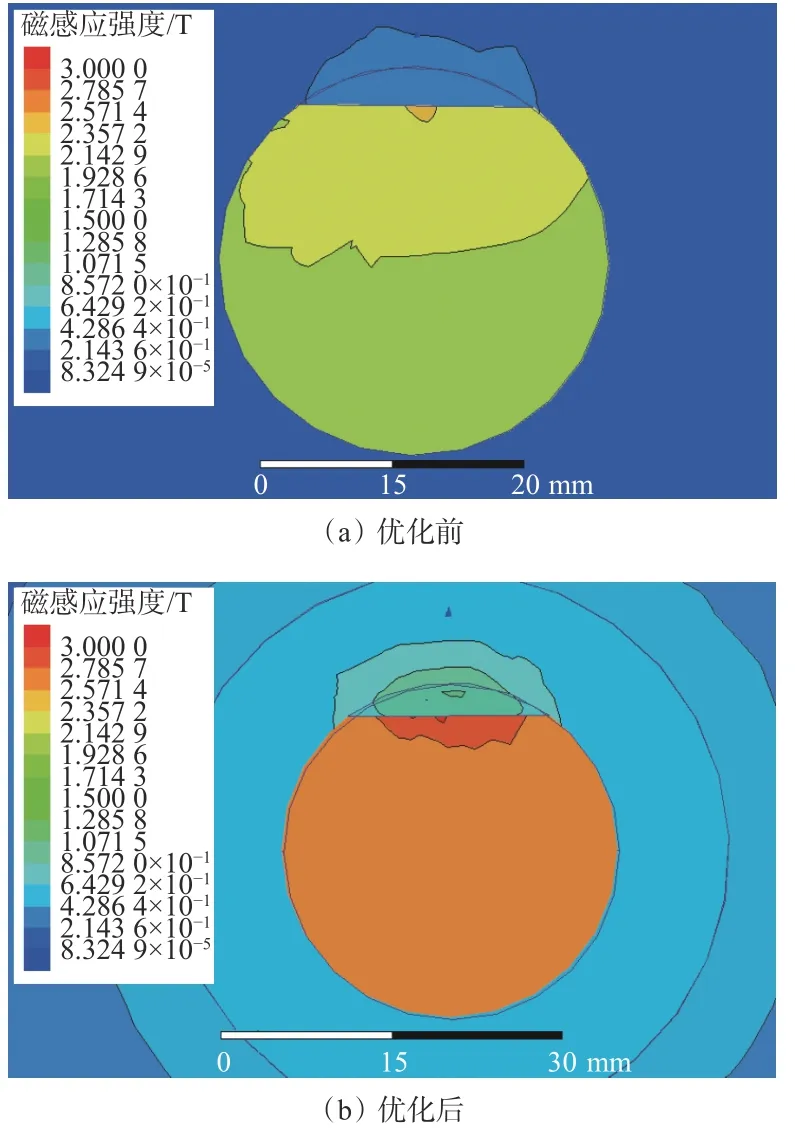
图9 优化前后钢丝绳探伤仪截面磁感应强度云图Fig. 9 Magnetic induction intensity cloud chart of section before and after optimization of wire rope flaw detector

对优化前后的钢丝绳探伤仪分别做了基于径向和轴向[20]2个方向的动态仿真，其结果如图10和图11所示。可看出优化后的钢丝绳探伤仪在径向检测方向上，其检测效果比优化前的探伤仪检测精度在峰谷值上提升了40%左右，而对于轴向检测方向的检测精度比优化前在峰值上提升约80%，漏磁的感知效果明显提升。

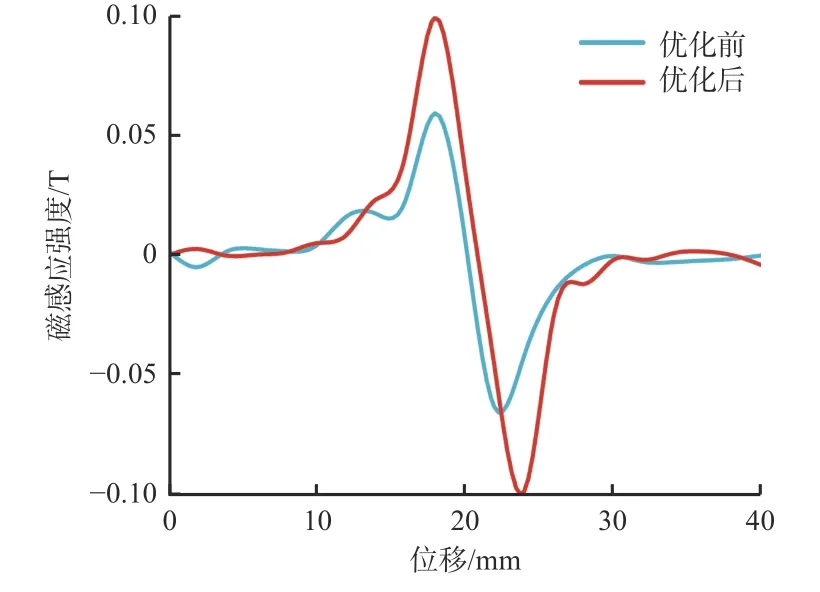
图10 径向漏磁比较Fig. 10 Comparison of radial magnetic flux leakage

4 结论

（1） 影响钢丝绳探伤仪检测精度的因素主要为衔铁的模型参数（长度、截面积）、气隙参数（宽度、长度）及磁铁参数（磁铁长度、厚度及两磁环的距离）。

（2） 在可控制的钢丝绳探伤仪参数中，各参数对钢丝绳探伤仪检测精度的影响等级为磁铁厚度、磁铁长度、衔铁长度、衔铁厚度和倒角情况。5个影响因素中，磁铁厚度、磁铁长度和衔铁长度影响显著，在设计钢丝绳探伤仪时应优先考虑，衔铁厚度及倒角显著性不强，可以忽略。其中 3个显著性因素中，磁铁厚度和磁铁长度（ ＜70 mm）的影响随着水平的增大整体呈正相关关系，而衔铁长度整体呈负相关关系。

（3） 基于正交试验的优化方法优化后的钢丝绳探伤仪磁力线分布均匀，对钢丝绳的励磁效果达到2 T以上，漏磁信号明显，不同相位下的损伤信号区别较大。与优化前的钢丝绳探伤仪相比具有磁感应强度大幅度提高、空域分布明显改善、对传感器布置位置（提离值）的要求相对宽泛的优势，径向检测精度提升40%左右，轴向检测精度提高约80%，对钢丝绳损伤的感知效果明显提升。

（4） 仅对钢丝绳探伤仪参数对漏磁检测影响进行了初步探究，仍有以下不足有待进一步探究：① 正交试验中各因素水平的选取覆盖不够全面，主要因素只取了5个。② 各因素水平也仅凭经验只选取了5个水平，且跨度较大。③ 未考虑探伤仪各结构参数之间的交互作用，比如磁铁长度和衔铁长度之间可能存在交互影响。④ 实际钢丝绳探伤仪的等效简化模型并非文中所示的等效简化模型，其他装配件可能对磁场也有一定的影响。