扭切式鼻坎挑射水流作用机理分析
2022-10-12吴锦钢周鑫宇葛亚飞黄梓涵
吴锦钢,邱 勇,周鑫宇,葛亚飞,黄梓涵
(云南农业大学水利学院,云南 昆明 650201)
0 引 言
泄水建筑物末端挑坎体型的选择是水利水电工程中消能防冲设计中的关键问题[1]。随着水利工程开发条件日趋复杂,传统的连续式鼻坎难以满足工程布置要求,需要在此基础上对体型作出相应的修改或者优化,得到能够改变出坎水舌空间形态或水股落点位置的异型鼻坎[2]。为此,许多学者在鼻坎体型选择以及水力特性研究方面做了大量的工作。练继建等[3]以提高消能率和减轻雾化现象为目的,探究了水舌在平面上对称横向扩散的舌型挑坎与连续坎水舌的液滴粒径与下游降雨强度分布规律;孙颖等[4]为防止下泄水流冲刷河岸,采用双曲型挑坎,使得出坎水舌在对冲后仍沿对称轴线方向扩散;Deng等[5]在针对大流量、窄河谷需要将水舌纵向拉伸情况下,优化出一种新型窄缝挑坎,结合数值模拟和模型试验,研究了水舌形态的形成机理;刘昉等[6]采用正交试验,对研究了扭曲式鼻坎中的参数变化对出坎水舌和下游河床的敏感性分析。
针对狭窄弯曲型河谷布置泄水建筑物,文献[7- 8]依托水工模型试验成果,采用扭切式挑流鼻坎,通过边墙的偏折,迫使水舌在平面上转向,给出了出坎水舌形态及水股落点,解决了水流平顺归河问题。本文采用连续性方程、动量方程、弯道超高经验公式结合冲击波理论,对扭切式鼻坎挑射水流作用机理进行分析,研究鼻坎内轴线立面挑射水流的水深和流速沿程变化规律、边墙偏转侧平面偏折水流水面超高经验公式以及底部斜射水流在出坎处的出射偏折角度。
1 反弧鼻坎水流结构分区
根据水工模型试验[7- 8]和数值模拟成果[9],扭切式鼻坎水流出坎后能够在空间上形成大面积的拉开,同时促使水股平面偏折,运动较为复杂。本文结合反弧段挑坎水流运动状态(见图1)的不同,将其概化为立面挑射水流、平面偏折水流和底部斜射水流[9],选取微元体进行受力分析。

图1 反弧段出坎水流平面形态
2 立面挑射水流
轴线附近直线前行的水流进入挑坎段后,水面沿反弧底板不断爬升、水深增加、流速降低。
2.1 连续方程
假定水流在轴线横向上呈均匀分布[10],流速分布沿水深满足幂指数分布规律[11],则水流的连续方程为
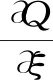
(1)
式中,Q为流量;ve为沿微元体法向距离鼻坎底部高度z的流速,m/s;v0为水流表面的速度,m/s;H为鼻坎内水流深度,m;m为幂指数的次数。
忽略指数m的沿程分布变化,连续方程可化简为
(2)
2.2 动量方程
选取反弧段鼻坎水流作为控制体,如图2所示,通过动量方程推求沿轴线方向的反弧段水流沿程水深和流速。
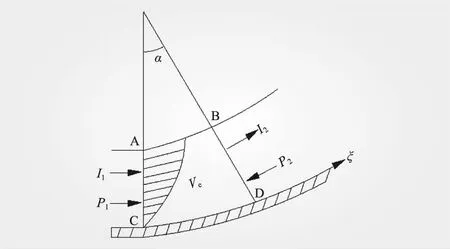
图2 反弧段动量方程控制体
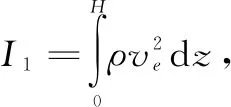
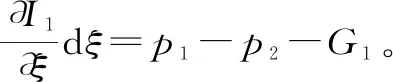
将动量变化量和外力作用项分别代入等式两边,得到
(3)
(4)
等式右侧,由于压强P沿程变化,其表达式仍需推导,同时假定水流流线沿水深分布均匀且不考虑水流在行进过程中边壁对水体产生的摩阻力[14]。
2.2.1 反弧段动水压强沿程分布
在上述反弧段上任取一段水深为H、长度为ds、高度为dh的单宽微元体,微元体轴线距离反弧段曲面底部高度为h,如图3所示。
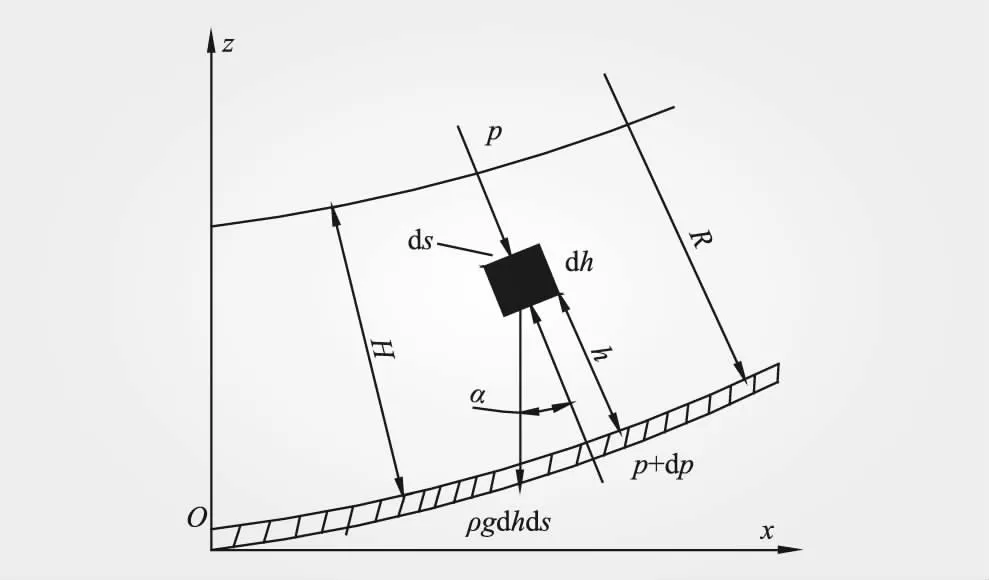
图3 动水压强微元体示意
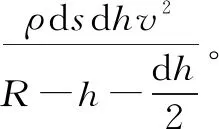
根据牛顿第二定律,微元体沿轴线的运动方程,可表示为
(5)
式中,ρ为水的密度,kg/m3;g为重力加速度,m/s2;R为反弧段结构半径,m;v为水流速度,m/s。
对于常数C,由边界条件(h=R-H)时,P=0,解出C=-ρv2lnH-pg(R-H)cosα,将C代入式(5),整理后得到反弧段动水压强沿程分布表达式,即
(6)
2.2.2 反弧段沿程水深和流速
基于上述分析,将式(4)、式(6)带入式(3)中,整理化简后得
(7)
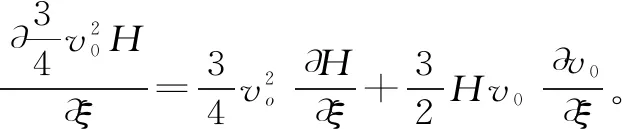
(8)
式(2)和式(8)构成反弧段封闭方程组,即
在此基础上,利用龙格-库塔法[15],可以求得反弧段的沿程水深H及流速变化v0。
基于该封闭方程组,结合挑流消能公式[16],可进一步计算出轴线附近的立面挑射水流挑距。
3 平面偏折水流
扭切式挑流鼻坎的一侧边墙以弧形向轴线方向偏转,上游端与边墙相切,下游端与反弧段末端轴线相接,其特殊体型使得水流结构发生变化,出坎水舌在平面上发生横向偏转[7],从而影响水舌落点的分布。
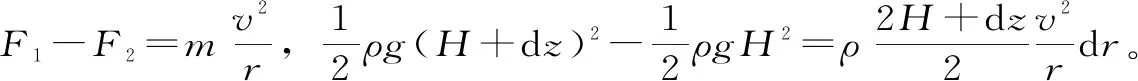
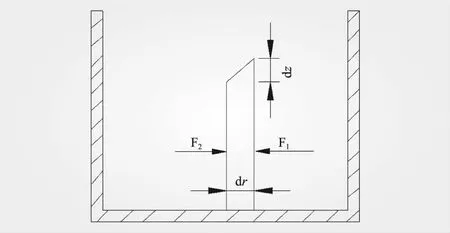
图4 弯道环流条形水体

(9)
式中,v为水流速度,m/s;r为左侧圆弧边墙的半径,m;B为鼻坎宽度,m。
弯道超高计算公式(9)在绝大多数情况下,其底坡为平坡或坡度很小,而扭切式鼻坎的底板曲率较大,水流爬升效应明显[18],对于超高的影响不能忽略。
考虑底板曲率的影响,计算该计算点(见图5)与前一点的高差Δz,Δz=R(cosα1-cosα2)。
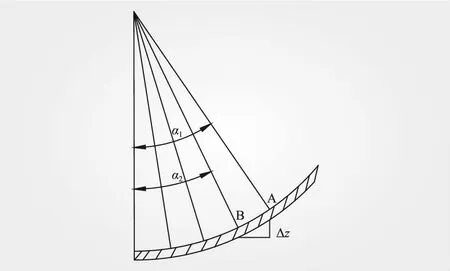
图5 反弧段等分
由于底板曲率的存在,使得爬升的水流超高值远低于底板为平坡时的数值[19]。若想要计算某一点的超高值,可将弯道超高理论计算值ΔH乘以这一点与等分后前一点的高差Δz。考虑到高差Δz带来的计算误差,引入一个调整系数k(反应底板曲率沿程对于超高计算的影响,则底板为曲面时该点的超高值可表示为
ΔZ=ΔkH×Δz
(10)
式中,k为调整系数,经试验率定,取值范围0.5~1.2。
根据式(10)计算结果,考虑相应安全超高,可以确定反弧段边墙高度。
4 底部斜射水流
泄槽水流进入挑坎段后,受弧形边墙的影响,水流沿边墙运动的同时,在边墙起始位置产生斜偏右方向的扰动水流。偏折水流如图6所示,将其运动方向分解为顺溢洪道轴线方向v′x和垂直于溢洪道轴线方向v′y。当沿轴线运动的惯性水流受到垂直于溢洪道轴线方向的水流挤压作用后,导致其运动向弧形边墙的另外一侧偏斜,偏斜水流运动至挑坎一侧后,在圆弧鼻坎出流处的水舌与轴线呈一小角度出射。
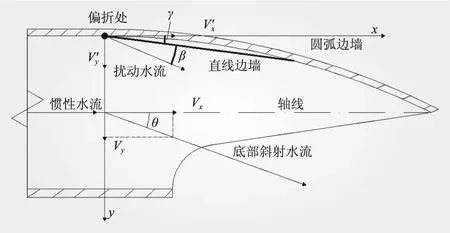
图6 偏折水流平面示意
直线边墙可采用IPEEN冲击波理论[20]计算扰动线的波角,而对于一侧边墙曲线型偏折,可看成是无数直线边墙的连续微偏折[21]。若直接将偏折处起点与终点相连接,误差将会偏大,于是作起点与终点连线的中垂线,中垂线延长至圆弧形成交点,连接起点与交点,形成新的直线边墙来代替圆弧边墙,再依次作中垂线,以无限逼近圆弧边墙。
将圆弧边墙作一次中垂线,把起点与交点相连的形成的边墙称为“直线边墙”,其与左侧直线边墙的角度为γ,扰动线与直线边墙的夹角β可采用下式计算为[22]
(11)
式中,Fr为偏折起点处水流弗劳德数。
水流在曲线型边墙的导向作用下,能量损失较小,扰动水流速度对偏折前的流速具有继承性[22]。将扰动水流速度分解,由几何关系有,沿y方向速度矢量v′y为
v′y=v×cos(90°-β-γ)
(12)
当沿轴线运动的惯性水流速度矢量vx(v′x)与边墙偏转所产生的垂向流速矢量vy合成后(忽略v′y沿y方向的速度衰减[23],即v′y与vy近似相等),轴线方向的惯性水流运动方向改变,斜向出挑,相撞击后的水流与溢洪道轴线的夹角θ为
(13)
通过值的计算θ值,可确定圆弧边墙对侧需要截断的边墙长度,以避免底部斜射水流出现水面沿边墙的壅高,影响水流挑射。
5 工程应用
某实际工程泄水建筑物出口轴线与河道交角过大,采用扭切式鼻坎挑流消将水舌平顺引入河道,挑坎反弧半径R1=10 m,挑射角度从左至右由25°渐变至57°41′50.230 6″,左侧圆弧边墙半径R2=12 m,消能防冲工况下下游消能防冲洪水标准为30年一遇(P=3.33%),泄洪洞相应下泄流量71.96 m3/s。
采用上述方法分别对泄槽轴线立面挑射水流水面线和流速分布、平面偏折水流超高进行验证,结果如图7~9所示。
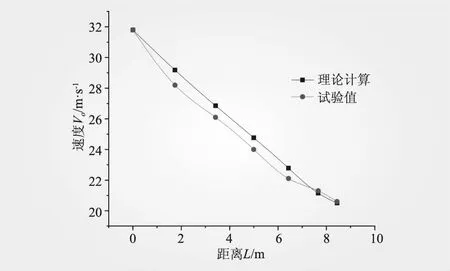
图7 反弧段轴线沿程速度对比
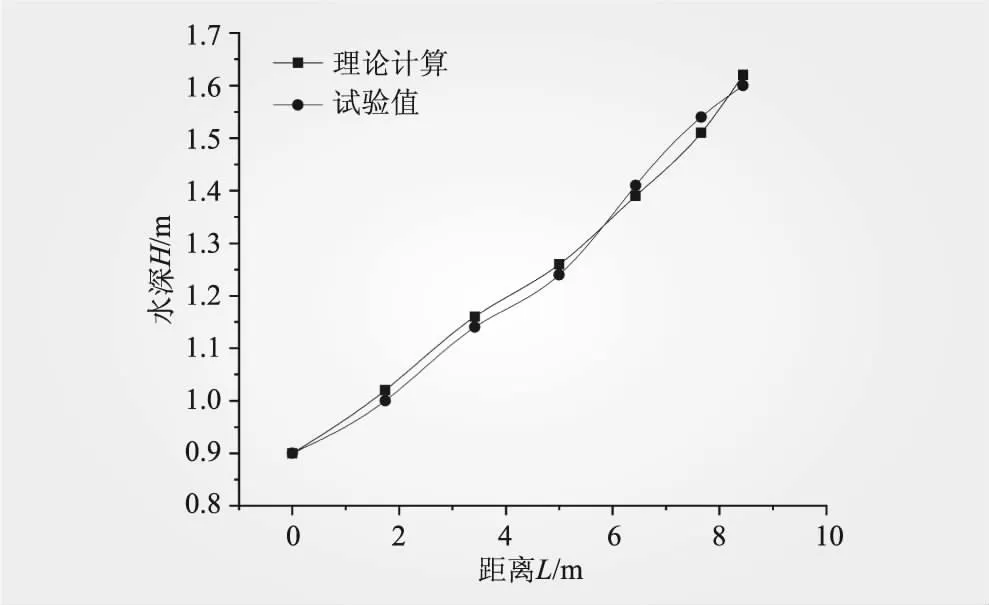
图8 反弧段轴线沿程水深对比
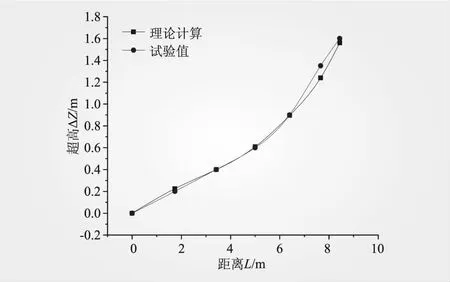
图9 偏转边墙水面爬升对比
由图7~9可知,根据连续性方程、动量方程和弯道超高经验公式,结合冲击波理论进行机理分析,所得到的坎内轴线立面挑射水流的水深、流速沿程变化公式以及边墙偏转侧平面偏折水流水面超高公式计算结果和试验研究成果误差均不超过10%。此外,底部偏折出挑水流的偏斜角度公式计算值为8.9°,与试验所得6.8°基本吻合。
6 结 语
本文结合水工模型试验和数值模拟所展现的扭切式鼻坎出坎水舌空间形态,将鼻坎内的水流分成立面挑射水流、平面偏折水流以及底部斜射水流三部分水流,结合其受力特点,采用连续性方程、动量方程、弯道超高经验公式结合冲击波理论,分别对水流作用机理进行了分析,可以得到:
(1)对于轴线附近的立面挑射水流,综合应用连续性方程与动量方程分析其坎内沿程水深与流速的变化,进而求得挑距。
(2)对于圆弧边墙处的平面偏折水流,基于弯道环流原理,利用经典的弯道超高公式,推导出底板为曲面时的超高值经验公式。
(3)对于圆弧边墙另一侧的底部偏折水流,基于冲击波理论,得到了扭切式鼻坎底部偏折出射水流与轴线夹角的经验公式,可为狭窄转弯河道挑流消能工程设计提供一定指导。
