风、浪、流荷载联合作用下海上升压站结构动力响应研究
2022-10-12张恒宇
徐 狄,张恒宇,陶 安,王 珂,苏 凯
(1.浙江华东工程咨询有限公司,浙江 杭州 310014;2.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122;3.武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
0 引 言
近些年来,随着陆上风电资源逐渐饱和,许多国家将目光转向了对海上风电资源的开发利用。与常规陆上风电相比,海上风电具有风资源稳定、发电寿命长、对环境污染少等优点。而海上升压站作为海上风电场的心脏,在海上风电场中起升压、中转的关键作用。
我国东部沿海强台风地区的海上升压站所处的海洋环境比较复杂,承受风、浪、流、地震等多种动荷载,引发的结构安全问题备受专家学者关注。目前,对海上升压站动力分析研究较多的是单一环境荷载作用下结构的动力响应,多种环境荷载联合作用下的动力响应相关研究较少。
在研究随机风、浪、流荷载计算与模拟方面,骆光杰等[1]基于谐波叠加法与Kaimal脉动风功率谱,编写了具备时空相关性的脉动风速时程模拟程序,并对比了模拟谱与目标谱;刘章军等[2]提出了正交展开-随机函数方法,模拟了脉动风速随机过程;Mardfekri等[3]基于线性不规则波理论,提出了随机波浪的概率需求模型;吕康玄等[4]基于波浪力的功率谱密度函数,开展了波浪力连续场的降维模拟,并给出了快速算法;张梦等[5]基于Borgman的条件模拟波浪理论,建立了将一特定短波列嵌入满足特定波谱的随机波列中的数值模拟方法;赵珂等[6]基于PM谱和简单方向分布函数,通过等分能量法、线性同余法离散波面方程,实现了三维随机波浪的仿真模拟。
在研究荷载对海上风电结构动力响应的影响方面,许洪露等[7]基于随机波浪理论和模态叠加法,研究了数值分析与理论公式求出的波浪动力放大系数的差异;廖迎娣等[8]基于建立的海上风电三脚架基础结构模型,研究了风、冰、浪、流荷载单独及联合作用下对结构动力响应的影响;陈小波[9]基于SPH和FEM耦合算法,开展了波浪对塔架-基础冲击过程的数值模拟,研究了波浪作用下近海风机塔架-基础的动力反应。
在上述研究基础上,本文基于有限元软件,建立海上升压站模型,进行模态分析,得到结构固有频率,分析相应振型。在模态分析的基础上,利用显式动力分析分别计算结构在环境荷载单独及联合作用下产生的动态响应,分析其规律及特性,以期为台风条件下海上升压站结构优化设计与建造等提供参考。
1 荷载计算方法
1.1 风荷载
自然风的风速一般分为平均风速和脉动风速两部分。平均风速的变化可采用指数函数来反映,任一高程处的平均风速为
(1)
式中,v(z)、v10分别为高程z和10 m处的平均风速,m/s;m为地表粗糙度系数。
脉动风速具有随机性,一般通过功率谱和相关函数描述。功率谱可以反映不同频率成分在整个风场中的能量分布,空间相关性函数可以反映不同位置风速点之间的相互关系。大多数国家在规范中使用Davenport谱在时域内描述脉动风速,Davenport谱是不随高度变化的[10],即
(2)
式中,Sv(n)为脉动风速功率谱,m2/s;f为脉动风频率,Hz;x为相似律坐标,x=1 200f/v10;k为地面粗糙度系数。
模拟脉动风速有线性滤波法、谐波合成法、小波分析法等[10-11],本文采用线性滤波法来模拟脉动风速。该方法根据计算模型的不同可以分为自回归模型(AR模型)、滑动平均模型以及自回归滑动平均模型[12]。本文基于AR模型的线性滤波法来模拟脉动风速。
根据规范[13],通过下式将总风速转换成风荷载
Ff=KKzp0A
(3)
式中,Ff为风荷载,N;K为风荷载形状系数,对平台总投影面积取1.0;Kz为风压高度变化系数,取1.235;A为垂直于风向的轮廓投影面积,m2;p0为风压,Pa,p0=αfvsum2,其中,αf为风压系数,取0.613,vsum为总风速,m/s。
1.2 波浪荷载
目前常用的波浪理论有线性(Airy)波、Stokes波、椭圆余弦波、流函数理论等[14-15]。线性波理论假设波高与波长的比值无限小,水质点以固定的圆频率w作简谐振动[16]。规则波浪场可以用线性波理论描述,而对于随机波浪场,可视为多个波幅、角频率、初相位不同的余弦波叠加[17]。故水质点水平速度vx和加速度ax以及单个波的波幅Ai为[18]
(4)
(5)
(6)
式中,φ为速度势;Ai、ωi、ki、εi分别为第i个波浪的波幅、角频率、波数、随机初相位;d为水深;z为竖向坐标;S(f)为波浪功率谱函数;Δω为将角频率等分为m份的份距。
波浪谱可以反映海浪在相应频率范畴内的能量散布情况,常用的波浪谱有P-M谱、JONSWAP谱等[19]。本文采用改进的JONSWAP谱[20-22],其功率谱密度函数为
(7)

对于D/L<0.2的小尺度结构物,可用Morison方程计算波浪力[23]。波浪力由拖曳力和惯性力组成,单位柱高的水平波浪力fH表达式如下[24]
(8)
式中,fD、fI分别为单位长度上作用的拖曳力和惯性力;ρ为海水密度;CD、CM分别为拖曳力系数、惯性力系数,本文分别取1.2、2.0。
1.3 流荷载
水平海流力表达式如下[14]
(9)
式中,Fc为作用在构件上的海流力,N;vc为海流流速,等于潮流可能最大流速和风海流可能最大流速的矢量和,m/s;Ac为垂直于流向的投影面积,m2。
本文直接将海流荷载与波浪荷载线性叠加,变成浪流联合荷载。
1.4 风、浪、流荷载的组合
对于目前海上升压站在多环境荷载作用下的动力分析,目前国际上多采用JC叠加原则[25]与Turkstra叠加原则[26]。本文采用Turkstra叠加原则,即轮番以其中1个载荷在设计基准期内的最大数值与其他载荷的瞬时值相叠加,当有n个可变载荷时,其叠加方式如下
Y1=maxX1(t)+X2(t*)+…+Xn(t*)
将接好菌的黄豆分装至纸杯中,每杯的豆子高度不超过4 cm,用保鲜膜封口后扎孔,放入生化培养箱中培养,于40 ℃发酵20 h左右[11]。
Y2=X1(t*)+maxX2(t)+…+Xn(t*)
…
Yn=X1(t*)+X2(t*)+…+maxXn(t)
(10)
式中,Xi(t*)为第i个荷载的瞬时值;maxXi(t)为第i个荷载在设计基准期内的最大值;Yi为第i个荷载组合。
1.5 阻尼
海上结构的阻尼是影响结构动力计算结果精度的重要因素。阻尼主要有气动阻尼、水动阻尼、结构阻尼、土体阻尼等[27]。本文只考虑水动、结构、土体阻尼,通过输入瑞利阻尼系数来考虑以上阻尼[21,24]。
C=αM+βK
(11)
(12)
式中,M、C、K分别为质量矩阵、阻尼矩阵、刚度矩阵;α、β分别为质量、刚度阻尼系数;ξ为结构的阻尼比,本文取0.04;f1、f2分别为结构的一阶、二阶自振频率。
2 海上升压站计算模型
2.1 工程概况
本文以广东某海上风电项目的海上升压站为研究对象,升压站电压等级为220 kV。该升压站包括上部组块和下部支撑结构。上部组块由四层钢结构甲板和直升机平台组成,标高分别为+13.50、+20.00、+25.00、+30.00、+33.25 m,平面主尺寸约34 m×36.6 m,采用空间钢桁架结构。下部结构采用四腿直桩式导管架基础结构。
2.2 计算模型及边界条件
图1为海上升压站结构计算模型。柱、梁分别采用S4R四结点壳单元、B31两结点梁单元模拟;舾装、固定设备等采用虚质量MASS单元施加于梁上进行模拟,焊接部分采用共节点方式模拟。计算模型共15 090个结点,15 322个单元。
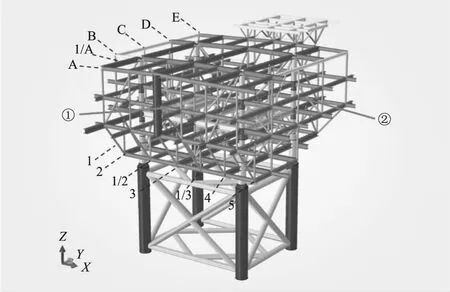
图1 海上升压站结构计算模型
对海上升压站四根钢管桩底部施加X、Y、Z向固定约束。
2.3 荷载施加及参数
由于本海上升压站位于台风地区,所以脉动风速考虑两种台风风速,分别为14级台风41.5 m/s、16级台风51.0 m/s。脉动风速模拟的范围为13.50~33.25 m高程,在+13.50、+20.00、+30.00、+33.25 m高程处分别取4个脉动风速模拟点,在+25.00 m高程处取8个脉动风速模拟点,共取24个脉动风速模拟点。风荷载作为集中力施加在两个参考点①、②上,参考点分别为A轴、5轴所在平面的中心点,高度为25 m,然后参考点通过耦合约束与A轴、5轴所在平面相耦合,受风面积分别为356、340 m2,模拟风时长100 s,时间步长0.1 s,脉动风速模拟具体参数如表1所示。

表1 脉动风速模拟主要参数
由于文章篇幅有限,选取10 m高度处的标准风速为51.0 m/s时,参考点①的模拟脉动风速时程及校核功率谱曲线如图2a、2b所示。
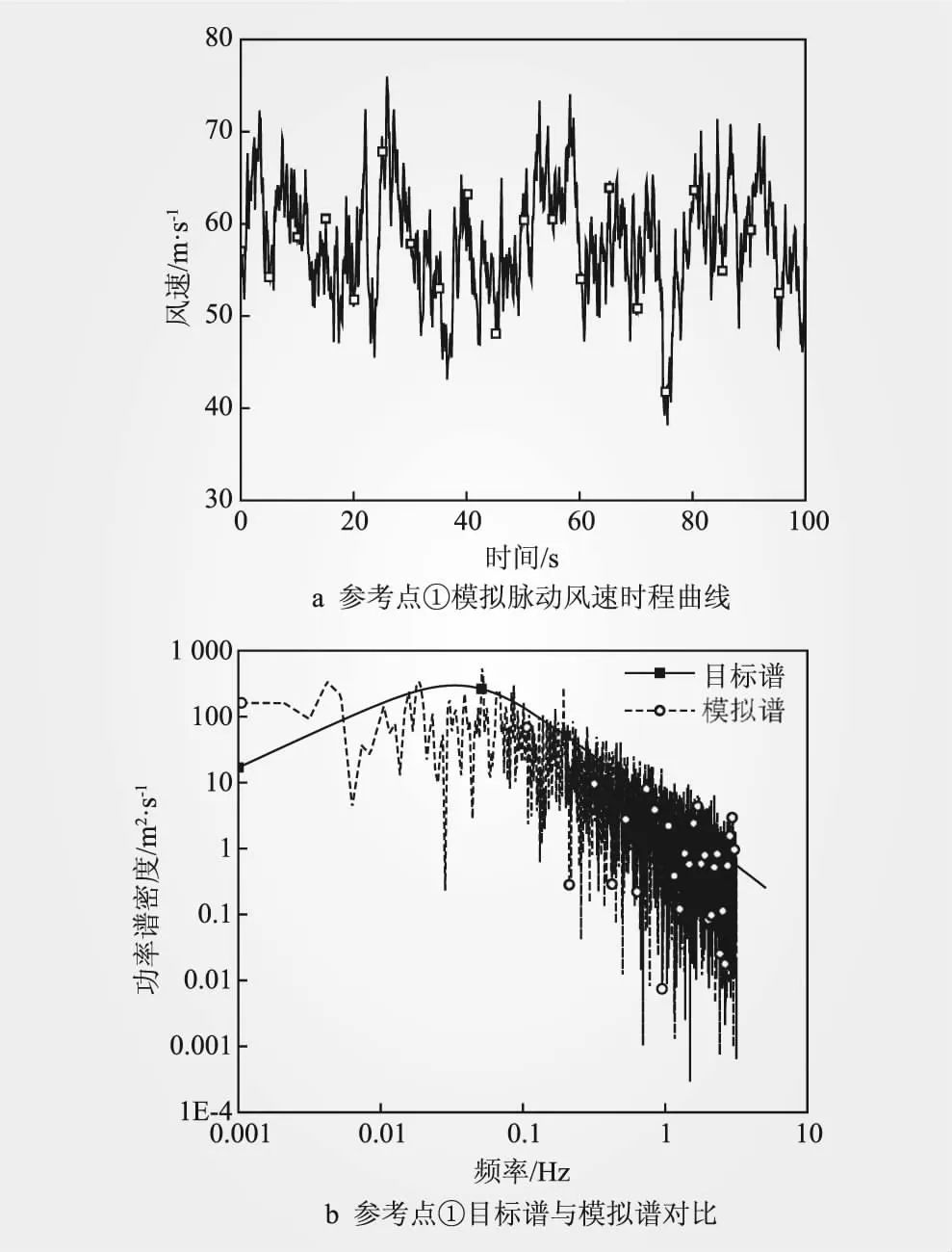
图2 脉动风速模拟
由图2b可知,模拟风速功率谱与目标谱虽然在低频区域(0.001~0.1 Hz)有一定差距,但是在0.1~5 Hz的区域两者基本吻合,说明基于AR模型的线性滤波法的脉动风速时程模拟效果比较好。
本文中,波浪荷载、流荷载作为集中力分别施加在4根下部钢管桩上,位置在水面处。钢管桩直径D=2.2 m,海水密度ρ=1 025 kg/m3,模拟浪、流时长100 s,依据工程资料,选取重现期分别为100年、2年的2组波浪参数,表2为水文参数。
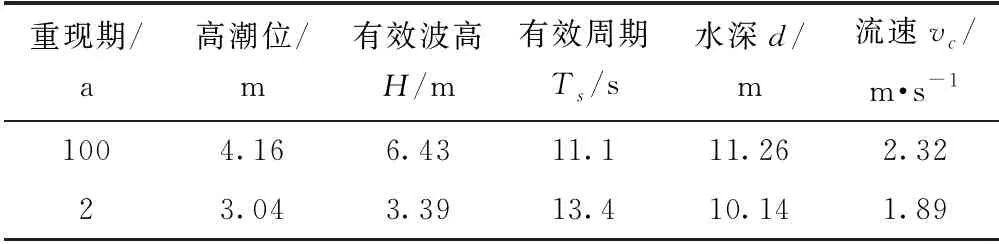
表2 海洋水文参数
本文采取等分频率法划分波浪频率区间,模拟能量谱的区间为0~4fpHz[29],谱间距为0.01 Hz,图3a、3b分别为模拟改进JONSWAP谱与PM谱的对比及重现期100年模拟浪、流荷载时程曲线。

图3 浪、流荷载模拟
由图3a可知,选择的频率区间范围良好,无论是改进JONSWAP谱还是PM谱,在边界处均趋于零,随着频率的增大,波浪能量先上升后下降,整个所围成的面积为波浪的总能量。在实际观测中,相同风速下改进JONSWAP谱的峰值与PM谱的峰值之比在1.5~6.0范围内[22],而图中模拟效果为两倍左右,满足要求。
3 模态分析
通过模态分析得到结构前六阶固有频率和振型如表3所示。
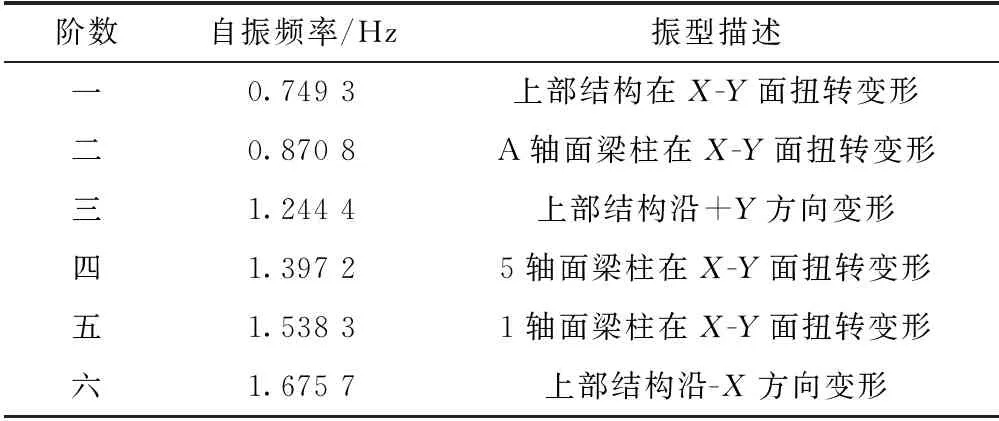
表3 结构前六阶自振频率和振型
由表3可知,随着振动阶数变大,其振动频率也随之变大,结构的自振特性是由其低阶特性所决定,故结构的固有频率为0.749 3 Hz,且前六阶振型除了变形部位不同,都是在X-Y平面扭转变形或者沿X、Y方向变形,说明该结构沿Z方向刚度较大,而沿X、Y方向刚度较小,水平荷载对结构的安全稳定影响较大,因此研究水平风、浪、流荷载对结构的动力响应很有必要。
由观测资料可知,波浪周期处于10.7~13.8 s,其需要避开的频率区间为[0.072,0.093]Hz,模型前六阶频率都不在共振频率影响区域,而且随着阶数的增大,其频率也随之增大,故结构可避免与波浪发生共振。根据第一、二阶自振频率,可计算出瑞利阻尼系数分别为:α=0.202、β=0.008。
4 动力响应分析
4.1 不同环境荷载作用下结构的动力响应
为研究台风、浪、流荷载对结构的动力特性的影响,采用4种荷载工况,如表4所示(荷载均垂直作用于A面,以下每种工况均未考虑恒、活荷载)。

表4 环境荷载工况
工况二的Mises应力与位移取得最大值的时刻云图如图4所示。

图4 工况二时刻云图
由图4可知,在只有浪、流荷载影响下,下部钢桩应力、位移响应最大,分别为41.81 MPa和0.25 cm,所处时刻为37.7 s,位于水面处,而上部结构响应很小,这是由于浪、流荷载作用在下部钢桩水面处,且下部钢桩顶端离水面有10.5 m远,难以传递到上部结构。
工况四的Mises应力与位移取得最大值的时刻云图如图5所示。

图5 工况四时刻云图
由图5可知,台风荷载单独作用下,应力和位移最大值均出现在A轴面梁处,分别为249.15 MPa和11.24 cm,出现在26.1、27.5 s时刻,各层梁与支撑柱交界处应力较大,直升机层和A轴面梁柱位移较大。
编写提取结构每一帧变量最大值程序,绘制工况一~工况四海上升压站整体结构最大Mises应力时程包络图和最大合位移时程包络图,如图6a、6b所示。
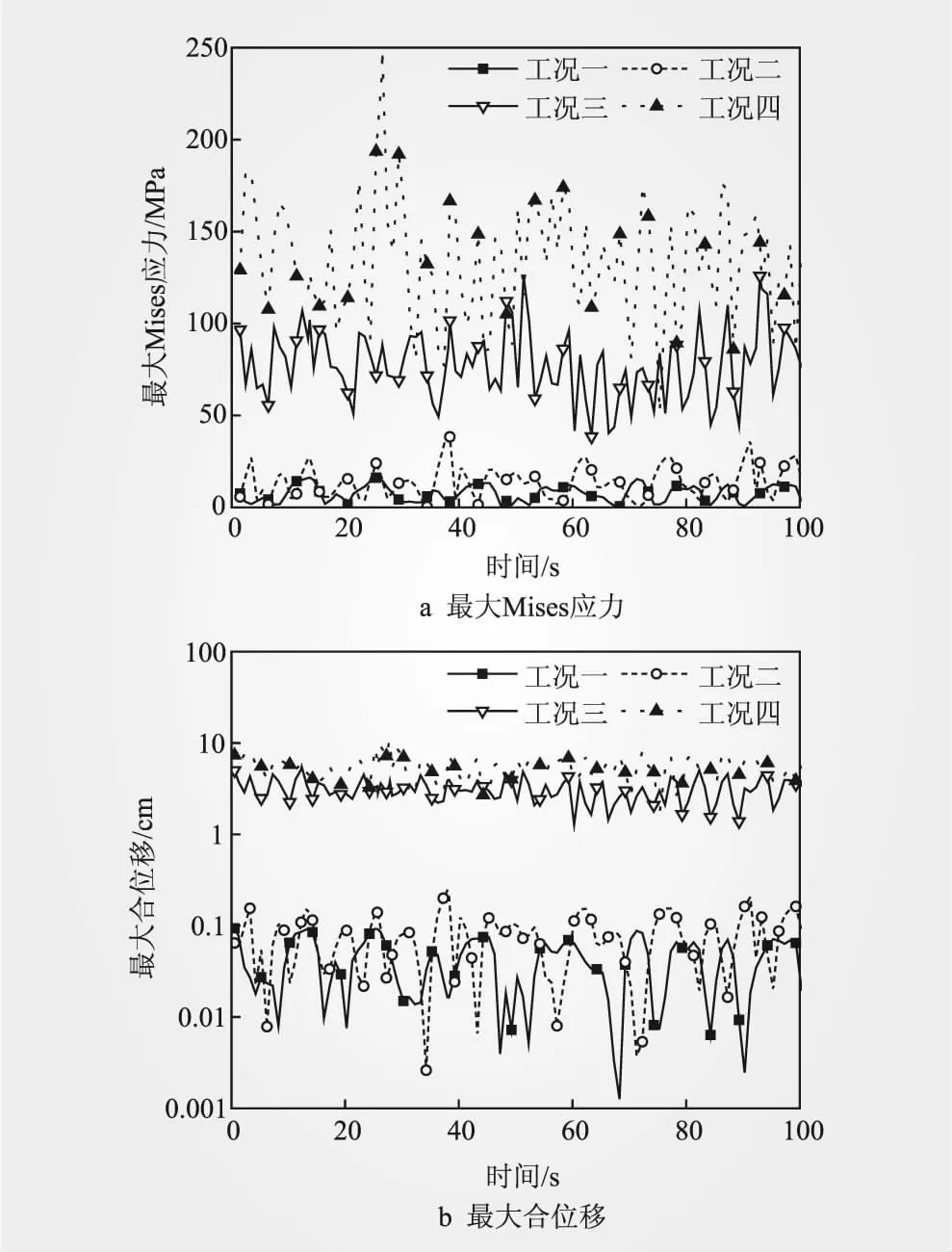
图6 工况一~工况四时程包络图
工况一~工况四的动力响应结果汇总见表5。
由图6和表5可知,结构的响应随着波浪重现期或台风风级的增大而增大,风荷载单独作用下应力、位移响应的最大值和变化幅度均远大于浪、流荷载作用。因此,在海上升压站结构的3种环境荷载中,风荷载是主控载荷,在结构整体响应中起主要作用。

表5 工况一~工况四下的动力响应
4.2 风、浪、流荷载联合作用下结构的动力响应
该结构主导荷载为风荷载,根据Turkstra准则将风荷载的瞬时值与该时段内浪、流荷载的极值叠加,从而得到多荷载耦合下的结构动力响应;由于该结构整体上近似为对称结构,所以只需要研究环境荷载在0°(垂直作用于5面)、45°、90°(垂直作用于A面)方向作用下对结构的动力特性的影响。本文采用如表6所示4种荷载工况(以下每种工况均考虑了恒、活荷载)。

表6 环境荷载工况
工况八Mises应力与位移取得最大值的时刻云图如图7所示。

图7 工况八时刻云图
由图7可知,工况八Mises应力最大值出现在位置5轴面梁柱与四层梁交界处,最大值为472.78 MPa,出现在26s时刻,且5轴面最上层梁普遍应力均大于200 MPa,而其他部位应力均很小,出现最大值部位附近的应力也均超过了DH36钢材的许用应力284 MPa,是工况八最危险部位。分析原因是风荷载垂直作用于5轴面时,C轴面最上层并没有设计轴向沿X方向的梁,只有A、B、D、E轴面的梁承受风荷载,且C轴面与5轴面交界的柱使用的是普通柱,没有使用如A轴面一样的吊机将军柱,导致了工况八5轴面应力较大,应当采取一些加固措施来防止破坏。工况八位移最大值出现在A轴面沿Y方向的外伸梁处,为23.06 cm,出现在25.4 s时刻,分析原因可能是在受到沿X方向的风荷载作用时,此外伸梁没有受到其他约束,导致了它容易沿-X方向变形。
绘制工况五~工况八结构最大Mises应力和最大合位移时程包络图,如图8所示。
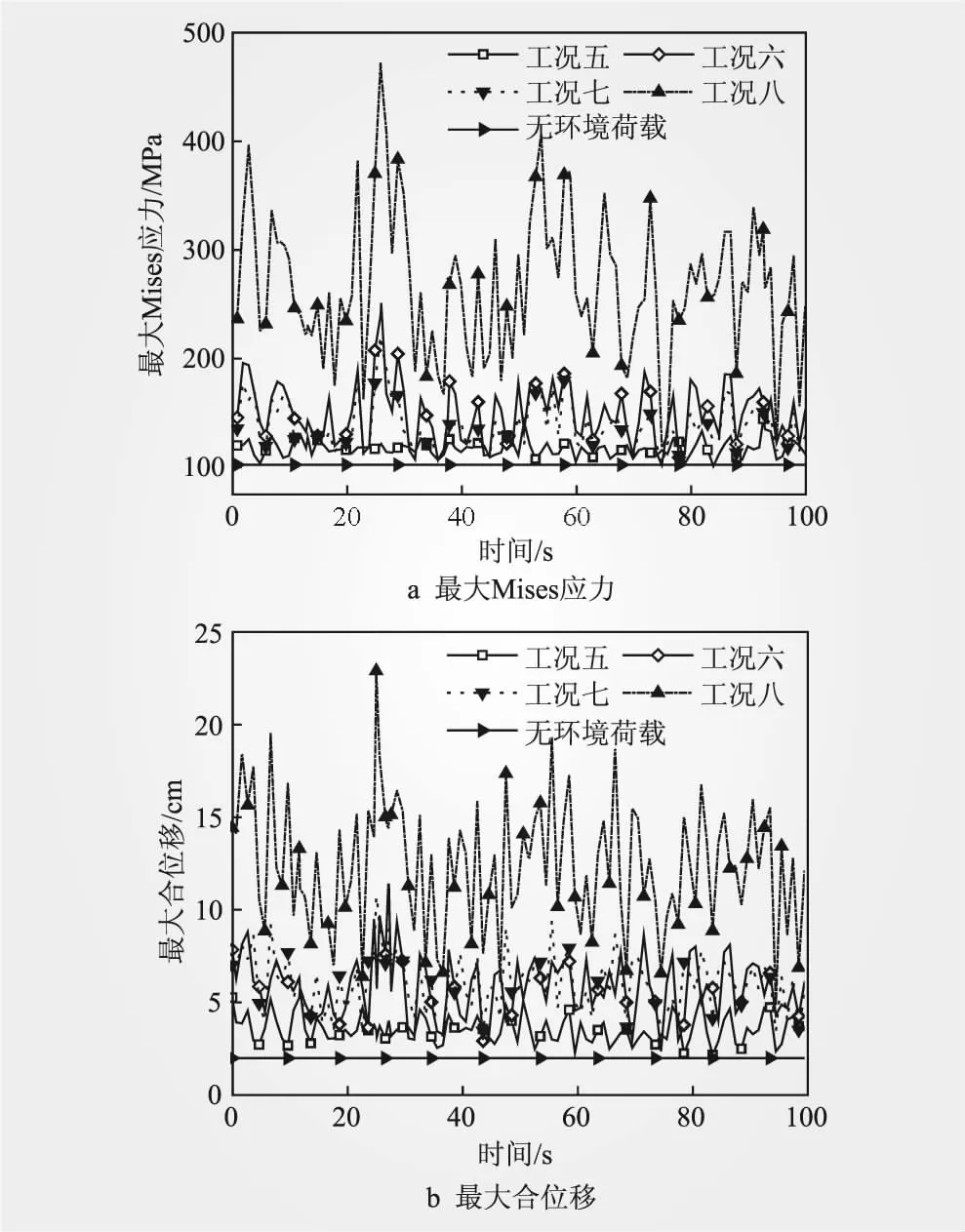
图8 工况五~工况八时程包络图
工况五~工况八下动力响应值见表7。

表7 工况五~工况八下的动力响应
由图8和表7可知,工况八下风浪流荷载垂直作用于5轴面时应力、位移响应最大,且变化幅度也最大;工况七下风浪流荷载沿45°方向作用时应力、位移响应最小,因此,在海上升压站结构中,风、浪、流荷载同时垂直作用于结构5轴面时,产生的影响最大,结构最为危险。
5 结 语
本文基于有限元软件建立海上升压站模型,并通过数学编程软件实现风、浪、流荷载时程变化曲线的模拟,最后进行了风、浪、流荷载动力响应分析。结论如下:
(1)模态分析结果表明,海上升压站结构沿X、Y方向刚度较小,水平荷载对结构的安全稳定影响较大;模型各阶频率都不在共振频率影响区域内,故结构可避免与波浪发生共振。
(2)不同环境荷载作用下结构的动力响应分析结果表明,结构的响应随着波浪重现期或者台风风级的增大而增大,结构在风荷载单独作用时产生的响应较大,而浪、流载荷产生的响应较小,风荷载是海上升压站结构的主控荷载。
(3)当风、浪、流载荷沿45°方向作用时,结构响应最小,沿0°方向(垂直作用于结构5轴面)作用时,结构产生的应力、位移响应最大,危险程度最高,在设计时应当增加C轴面与5轴面交界处柱的厚度,且要在C轴面最上层增加轴向沿X方向的受力梁来防止破坏。
