融合信任圈和移动模式的位置预测框架
2022-10-12魏盛杰
魏盛杰,王 鑫,戴 劲,韩 楠
(1.四川音乐学院 实验艺术学院, 成都 610021;2.成都信息工程大学 软件工程学院, 成都 610225;3.四川音乐学院 美术学院, 成都 610021;4.成都信息工程大学 管理学院, 成都 610103)
0 引言
基于位置信息的社交网络(location based social network,LBSN)在瞬息万变的时代中应运而生,得益于智能移动设备的广泛普及与移动定位技术的飞速发展,个体用户的位置信息数据比以往任何时候都更容易获取。众多基于位置的社交网络(简称位置社交网络)平台,如:Foursquare、Facebook Places以及微信、美团、大众点评等,它们将用户的线上活动与线下生活建立联系,有效地将现实生活与虚拟世界结合在一起,打破了存在于物理世界与网络世界之间的信息鸿沟。
由于签到数据集包含了丰富的信息,现阶段有越来越多的研究者利用签到数据来预测用户的下一个签到点。传统的研究主要是利用用户的个体移动模式来预测下一签到位置,仅仅考虑历史签到记录的预测模型性能是有局限性的,它的弊端在于没有综合考虑用户的移动模式以及用户的社会信任关系这两类影响因子,缺乏考虑位置属性与用户特征之间的关联性。
在部分情况下,用户的社交关系在一定程度上会对用户的时空行为构成影响[1],例如,当用户与信任度高的朋友在餐厅共进晚餐的时候,下一步计划更大概率会采取该朋友提出的建议,并且长期处于同一社交圈内,不同用户之间的兴趣爱好会逐渐统一化。生物的移动模式通常会受到个体属性以及群体属性的影响,即用户的移动行为并不是固定不变,而是会随着环境变化而变化[2]。本文研究目标旨在开发一个有效的位置预测框架,综合考虑用户的信任圈以及移动模式来精准预测用户的下一个签到位置。
本文针对预测用户下一个签到位置问题提出了一种融合信任圈和移动模式的位置预测框架FTM(a location prediction framework based on trust circle and mobility pattern)。具体来说,该框架分为2个模块:① 信任圈模块;② 移动模式模块。本文首先介绍了基于位置社交网络的综合研究。其次,本文利用信任关系对个体的影响挖掘出一种新型社会关系,接着根据用户签到模式表现出的周期性提出了直接访问模式及多元访问模式。最后,本文在真实数据集上评估了模型的性能。实验结果证明,本文提出的模型可以很好地预测用户下一个签到位置。
综上所述,本文的主要贡献包括:
1) 基于位置社交网络利用用户的新型社交关系和移动模式预测下一个签到位置。
2) 提出了信任圈的新概念,将信任圈按照不同群体划分为三类社交关系,对用户时空行为的影响进行建模。
3) 将移动模式拆分为直接访问模式及多元访问模式,对不同访问模式造成的影响进行建模。
4) 在大规模真实数据集上评估了FTM预测框架,实验在准确率以及鲁棒性上都优于其他代表性方法。
1 相关工作
作为异构网络中的典型代表,位置社交网络中蕴藏着十分复杂的结构,位置社交网络信息层次如图1所示,主要可以分为4层。
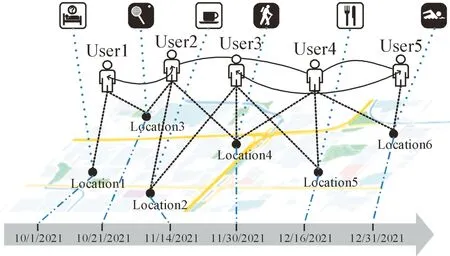
图1 位置社交网络信息层次图
图1由下至上依次为时间信息层、地理信息层、社交信息层以及文本信息层,每一层包含了多个节点(例如时间节点、位置节点和用户节点等),位置网络将多种不同类型的节点相互连接起来,构成了多元的关联关系(例如User1和User2之间的社交关联以及User1和Location1之间的签到关联),从而可以更精准地分析用户的行为和特征。从图1中可以发现:User1与User2分享位于Location1的签到信息,不仅交换了地理层面的签到信息,还额外产生了时间层面信息、文本层面信息以及社交层面信息,多个层面的上下文信息会在潜移默化中影响到User2下一步位置的选择。位置社交网络将不同层面的信息关联起来,可以精准快速地挖掘用户的潜在兴趣、用户的行动规律以及不同用户之间的社交关系等内在信息。因此,利用大量的签到数据为基于位置服务的研究提供了新的技术思路,如预测用户的下一个签到位置、POI推荐、城市计算等[3-4]。
当前,位置预测已经成为基于位置社交网络的主要研究任务之一。位置预测指的是利用用户在位置社交网络中的历史签到记录,捕捉用户移动的规律性,进而对用户下一个可能访问的兴趣点进行预测。考虑到位置社交网络中上下文信息的多样性以及人类移动模式的特异性,具有不同特性的人群通常其规律性并不能完全吻合。因此,在满足用户个性化需求的情况下来挖掘用户移动方式的规律性已经成为改善用户生活质量以及提高位置服务市场效率的重要环节。
目前针对位置社交网络中位置预测的研究主要集中在以下3个方面:
1) 基于序列模式的位置预测。按照时间顺序将用户所有的历史签到点记录作为一个序列,通过计算某一地点在该序列中出现的频率并且挖掘它与相邻地点之间潜在关系来进行位置预测。
2) 基于时间动态性的位置预测。通常情况下,用户在签到时会附带时间戳信息。通过挖掘用户签到行为时呈现出的周期模式,分析地理位置变迁与时间推移的高相关性来进行位置预测。
3) 基于社交关联性的位置预测。采用用户好友的签到历史记录推断用户的签到行为偏好,将时空关系和社交关系紧密结合在一起来进行位置预测。
在基于序列模式的位置预测研究方面,Yin等[5]提出了签到最高频次模型,该模型主要应用于仅收集到签到历史记录但没有上下文信息的情况,通过计算下一个的签到位置在历史记录中出现的频率来计算该位置在下一次出现的概率。在此基础上,Gambs等[6]提出了K阶马尔可夫模型,该模型将下次签到之前的K个签到序列作为签到上下文,然后计算签到历史记录中上下文序列出现的频率作为下一个签到位置的概率。为了避免在历史记录中找不到签到上下文序列的情况,动态改变K的大小,当K=0时,该模型退化成签到最高频次模型。
在基于时间动态性的位置预测研究方面,Gao等[7]提出利用用户签到数据中体现的时间周期性进行建模,对用户将来签到的位置进行预测。Valverde-rebaza等[8]对时间周期性进行了拓展,基于用户活动的循环模式提出了一种应用于签到位置预测的通用型时间框架,该框架主要采用混合高斯模型来描述用户在签到位置的时间周期性特点。
在基于社交关联性的位置预测研究方面,Li等[9]提出了基于序列的社交可移动模型,该模型通过分析好友签到行为模式来推断用户的签到行为偏好,并且结合时空信息,计算好友签到序列对用户当前签到可能性的大小,从而预测用户下一个访问的位置。
基于位置社交网络的位置预测已经取得一些研究成果,但是预测的准确率无法满足用户的需求,如何更加全面地考虑和混合多源异构信息是需要进一步研究的问题[10-11]。本文所提框架的创新性在于不仅考虑了信任圈的影响,并且在此基础上加入不同移动模式对位置预测的影响,与已有工作相比,本文提出的框架考虑更为全面,预测结果更加精准。
2 问题表述与模型
2.1 信任圈的特征
通过分析流行位置社交网络,如Gowalla数据,用户的签到行为可以分为以下2种情况:第一种是用户只身一人的签到行为,另一种是用户与某一社会关系同时出现的签到行为。与用户在同一位置签到的人群可以分为信任朋友、地理邻居以及陌生人这三类群体。基于此,本文提出了信任圈的概念,并按照不同群体划分出三类社交关系,为了更好地解释信任圈对用户产生的影响,下面分别对以下三类社交关系的特征进行详细描述。
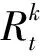

定义3:共现关系(co-occurrence relation)。将位置社交网络中在同一位置签到的用户定义为共现关系,并用符号Rc表示与用户有共同签到记录的社交关系的集合。
图2为三类社交关系在累计签到数增加情况下的共现率分布变化图。其中,x轴表示已统计到的用户签到数,y轴表示共现的概率。

图2 信任圈的共现分布曲线
从图中可以发现,在已统计到的签到集中,1 500次累计签到数内每类社交关系的共现概率都在30%以内;随着累计签到数量的增加,共现率也会增加,并且最终趋于稳定。主要有以下3个原因导致这种趋势:① 用户将POI分享给其社交关系导致共现行为;② 用户在使用签到程序的初期缺少历史记录导致起始阶段的共现率较低;③ 随着时间的推移,签到数据逐渐完整,社交关系也逐渐稳定,共现率最终呈现平稳的状态。
2.2 移动模式的特征
为了模拟信任圈的影响,本文同样分析了Gowalla数据集上用户的签到模式。文献[12]研究表明,人类的签到模式主要以日模式和周模式表现出周期性的循环,即一天和一周代表人类活动的主要循环周期。因此,本文的分析沿用了这种时间周期模式,利用日模式和周模式在结构上的相似性挖掘具有代表性的用户移动模式。本文将一天按照小时进行“切片”,将用户所有的签到记录按照时间顺序投影到24个片段内,并且对每一个小时内的签到频率进行统计,从而得到了日模式下的用户签到频率图[13],如图3所示。
从图3可以发现,用户的签到主要集中在早上8点至晚上8点之间,并且1 d中的签到高峰期出现在晚上7点左右。本文将每天的签到记录按照日期顺序投影到1周内,得到了图4所示的周模式用户签到频率图。
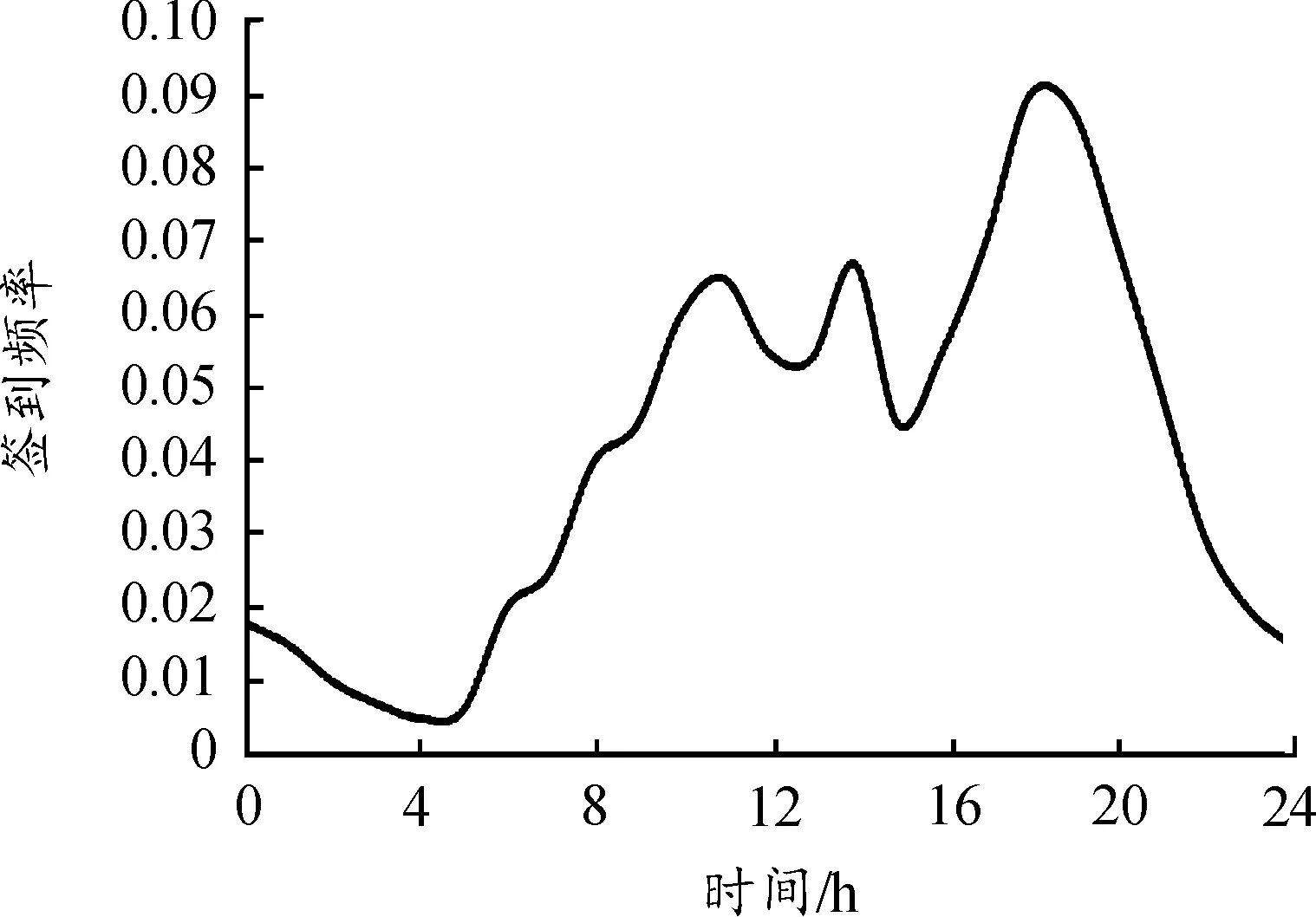
图3 日模式用户签到频率曲线
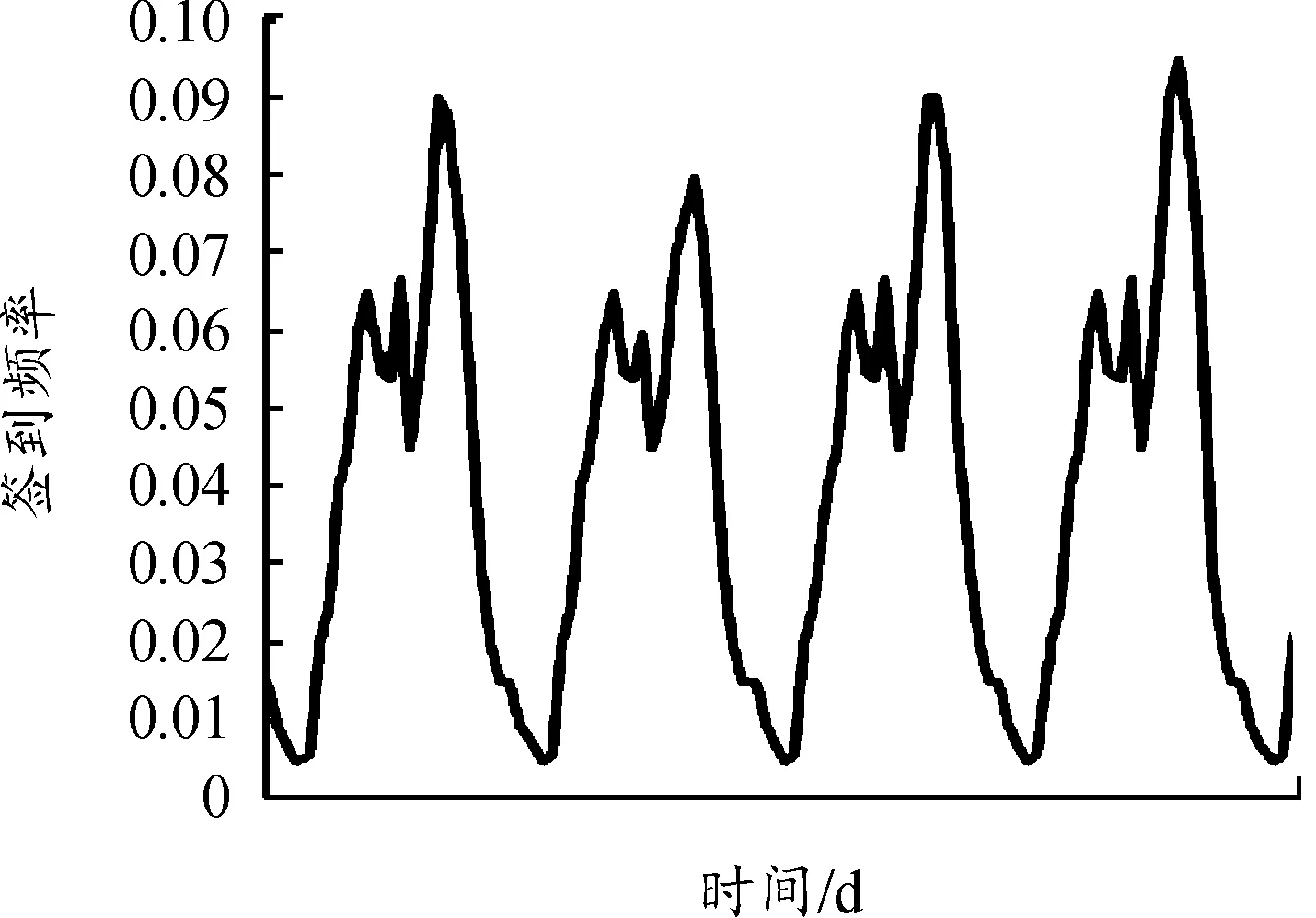
图4 周模式用户签到频率曲线
从图4可以发现,在周模式下,用户在工作日的签到模式相对一致,而周末的签到频率相较于工作日有所下降,主要是由于用户在周末更可能选择居家休息[14],说明用户在周末的签到存在不规律性,本文通过计算周模式的平均签到频率来解决周末位置预测相对困难的问题。由于用户轨迹呈现出周期性的重复,所以本文利用Apriori算法[15]来提取用户的移动模式。
定义4:个人移动模式(individual mobility pattern)。用户U的移动模式是根据其签到路线按照时间顺序频繁访问的位置序列,其频率不小于最小支持度Smin。第一步采用基于位置序列的方法挖掘用户的轨迹序列,第二步从挖掘到的所有频繁序列中找出最大频繁子序列以确保具有大片相同片段的子序列是属于不同时段的。
定义5:群体移动模式(crowedmobilitypattern)。表示所有个人移动模式的集合。由于人们经常遵循相似的运动模式,所以利用可用用户的轨迹来代表一群人的全局行为是可行的。利用每个用户的历史移动轨迹挖掘其移动模式,然后将它们合并以用于下一步的预测。
2.3 问题定义
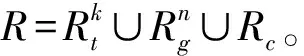
用户的下一签到位置主要受到2个方面的影响:信任圈以及移动模式的影响。因此,将预测用户下一个签到位置问题形式化:当已知集合Ct和Ch时,目标是计算出用户在t时间访问下一个签到位置l的概率。基于以上形式化定义,本文将位置预测概率定义为:
P(l)=P(l|Ct,Ch)
(1)
信任圈以及移动模式的影响力可以作为2个独立的模块,采取类似于文献[16]提出的组合方法来计算位置预测概率:
(2)
其中,λ表示一个控制信任圈关系以及个人历史移动模式的影响权重的常数参数。
2.3.1信任圈的影响力
在本小节中,通过计算信任圈系数来测量三类社交关系对用户的影响力。利用加权的方法,信任圈的模型可以进一步展开为:
(3)
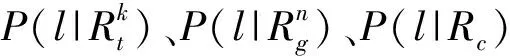
通过分析图2,发现3个社交关系的函数曲线类似于S形函数,即:随着累计签到数量的增加,用户之间的共现率随之增加,并且最终趋于稳定。因此,本文将相关系数θ1、θ2、θ3作为激活函数:
(4)
其中,f1表示k阶信任关系中的用户签到特征向量,W1表示特征向量f1的权重矩阵,b1表示偏置项。相关系数θ2和θ3的定义如下:
(5)
(6)
其中,f2表示n度邻近关系中的用户签到特征向量,W2表示特征向量f2的权重矩阵,b2表示偏置项。f3表示共现关系中的用户签到特征向量,W3表示特征向量f3的权重矩阵,b3表示偏置项。
(7)
考虑到信任圈的多元性,本文融合信任圈关系和签到位置关系来计算相关系数,如式(8)所示。

(8)
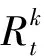
2.3.2用户移动模式的影响力
用户移动的模式可以分为两类:一种是用户u直接从目标位置lj到侯选位置lk的情况,称为直接访问模式,用符号M表示;另一种是用户u从目标位置lj到侯选位置lk之前还访问过其他位置的情况,称为多元访问模式,用符号M*表示。不同的移动模式在模型中占有不同的权重,因此,利用加权的方法,用户移动模式模型进一步展开为式(9)。
P(l|Ct)=ηP(l|M)+(1-η)P(l|M*)
(9)
其中,η表示一个控制不同移动模式权重的常数。
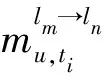
(10)
为了方便计算从位置lx到位置ly之间的移动概率,将观察到的所有用户uj在时间ti从当前位置lx到目标位置ly的移动转换列举出来,并利用式(11)计算群体移动模式。
(11)
因此,直接访问模式下的概率模型可以扩展表示为:
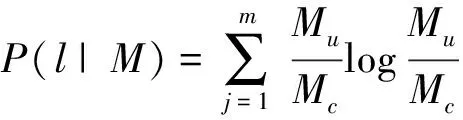
(12)
2) 多元访问模式:由于签到集中可能存在数据缺失的情况,本文提出了多元移动模式,即用户u从当前位置lx到目标位置ly的移动过程中额外至少经历过(n+1)个位置。
给定当前位置ly时,计算在t时刻它作为目标位置的概率,即数据集中所有其他位置在时间t到达位置ly的移动行为的概率,计算公式如下:
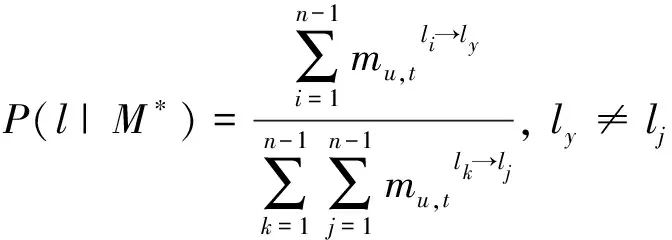
(13)
2.4 融合框架
本文提出了融合信任圈和移动模式的框架FTM用于预测用户的下一个签到位置。根据式(2)和(9),框架FTM最终定义为式(14)。
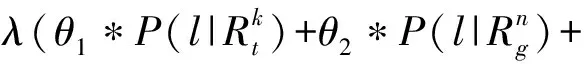
θ3*P(l|Rc))+(1-λ)(η*P(l|M)+
(1-η)*P(l|M*))
(14)
3 实验结果与分析
本节将介绍实验环境、数据集、评价指标、基准方法、参数选取与实验分析。为了验证提出的FTM框架的性能,本节工作包括:分析了FTM框架中不同因素的影响权重,通过评估其在不同设置的实验条件下的准确率来确定实验参数;与其他具有代表性的先进算法对比预测结果的准确率并分析造成差异的原因;通过改变空间阈值来分析FTM框架的鲁棒性。
3.1 实验环境
实验硬件环境如表1所示。

表1 实验环境
3.2 数据集介绍
为了评估FTM框架的性能,在公开数据集上进行实验。由于模型中使用了信任圈模块,本文使用递归神经网络来计算用户的家庭位置。为了保证实验的有效性,实验中筛选至少包含80条签到记录的用户,并且删除了不满20条签到数据的位置数据。为了避免实验结果的偶然性,本文根据用户的签到时间将数据集划分为训练集和测试集,按照时间顺序,每个用户的70%的签到记录用于训练,剩下30%用于测试,实验数据集参数如表2所示。

表2 实验数据集参数
数据集描述如下:
1) Gowalla数据集:该数据集包含3 112名用户在3 298个地点27 149条附带时间戳的签到记录,其中包括3 776条用户社会关系记录。
2) Foursquare数据集:该数据集包含来自923 506名用户在4 960 482个地点35 289 629次附带时间戳的签到记录,其中包括4 751 635条用户社会关系记录。
3.3 评价指标
本文使用预测准确率指标Accuracy来评价模型的性能。计算每个候选位置的概率后,返回排名top-N作为预测的结果。只要用户的实际签到位置出现在top-N中就认为预测是准确的[18]。采用Accuracy@N表示不同N取值的预测准确率,在实验中N的取值为1、5、10。
3.4 基准方法
为了说明FTM框架位置预测的性能,本文引入以下方法进行比较。
1) MFC(mostfrequentcheck-inmodel)模型[19]是预测用户下一签到位置的经典指标,该模型将用户u在位置l签到的概率定义为位置l出现在用户u的签到历史记录中的概率。
2) FSM(feature-based supervised model)模型[20]提出了最直接竞争对手的概念,利用一组描述用户运动模式的时空特征矩阵来预测下一签到位置,在此基础上将这些特征组合到监督学习模型中。
3) FPM (feature-based personalized model)模型[3]基于矩阵分解的方法嵌入个性化马尔可夫链。该模型不仅改进了签到序列中的个性化马尔可夫链,还考虑了在局部区域内用户移动行为中存在的约束因素。
4) PSMM(periodic social mobility model)模型[21]通过观察用户在一天中的某些时间段表现出的强烈周期性行为,计算目标用户在目标时间内最有可能停留的区域,达到预测用户下一个签到位置的效果。
5) PRED(periodic region detection)模型[22]是贝叶斯非参数模型,通过混合地理信息和时间信息建模来发现用户的周期性流动模式。由于其为非参数的模型,所以不需要关于个体流动性的先验知识。
3.5 参数选择
在选择参数λ和η时,它们的取值在0~1变化,进行了200次实验,步长增量设置为0.05。
从图5和图6中可以发现,当λ=0.25,η=0.75时FTM可以达到最佳性能。参数λ用于控制信任圈模块的权重,将η固定为0.75,以0.05为步长将参数λ从0增加到1,从图5中可以发现,当λ=0.25时达到最高准确率。当λ=0.05时,这种情况几乎只考虑用户的历史移动模式,没有考虑信任圈的影响,实验结果表明它的准确性不是最佳,进而表明不能仅考虑用户的历史移动模式,需要进一步考虑额外的影响因素,个体用户的时空行为并不是一尘不变的,具体来说需要重视社交关系对用户判断产生的影响,当提高信任圈模块的权重时,模型的准确率会提升;当λ=0.25时,预测准确率最高,模型的预测性能达到最佳,说明它是信任圈和移动模式模块的最佳权重。
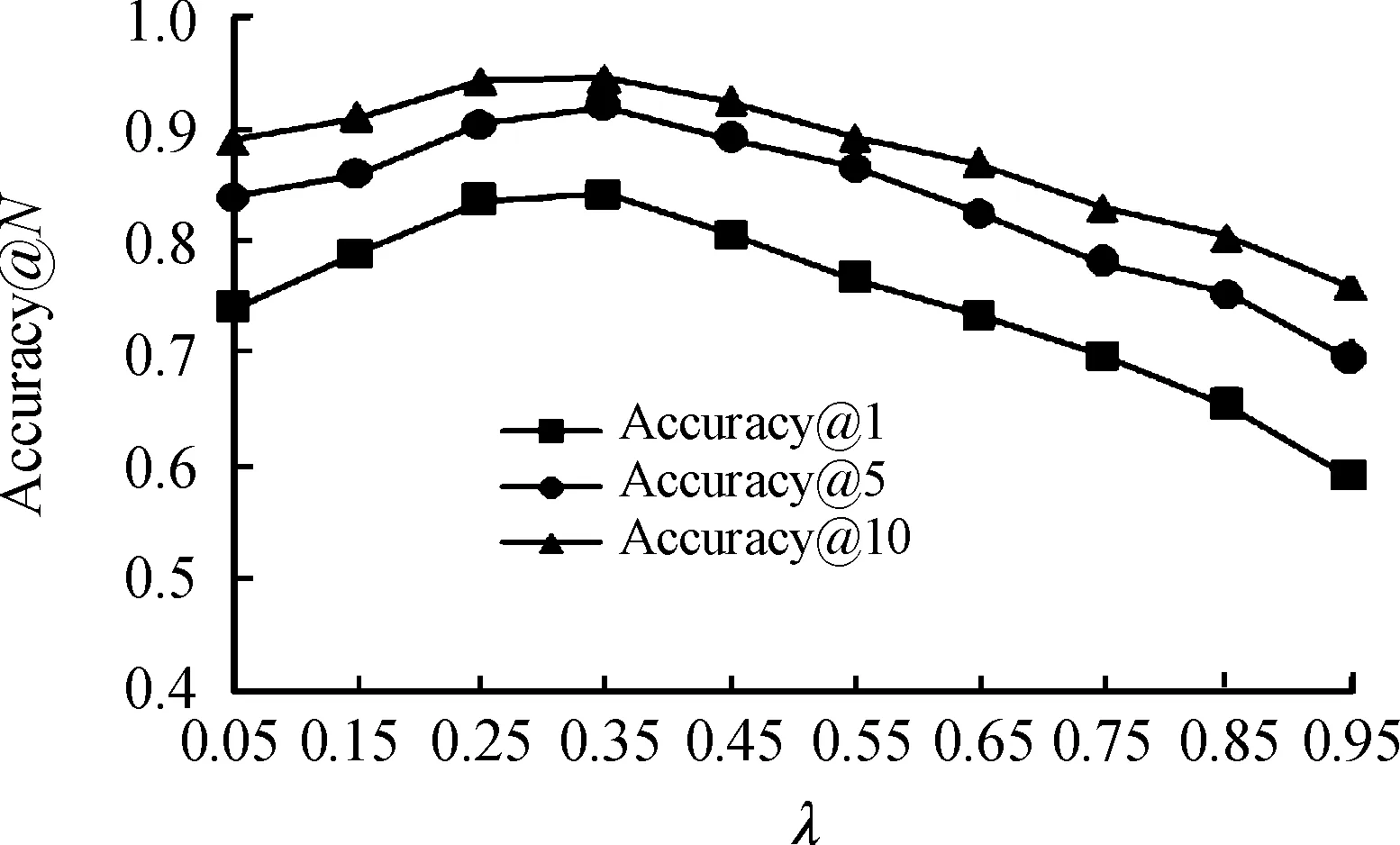
图5 不同λ值下的预测准确性
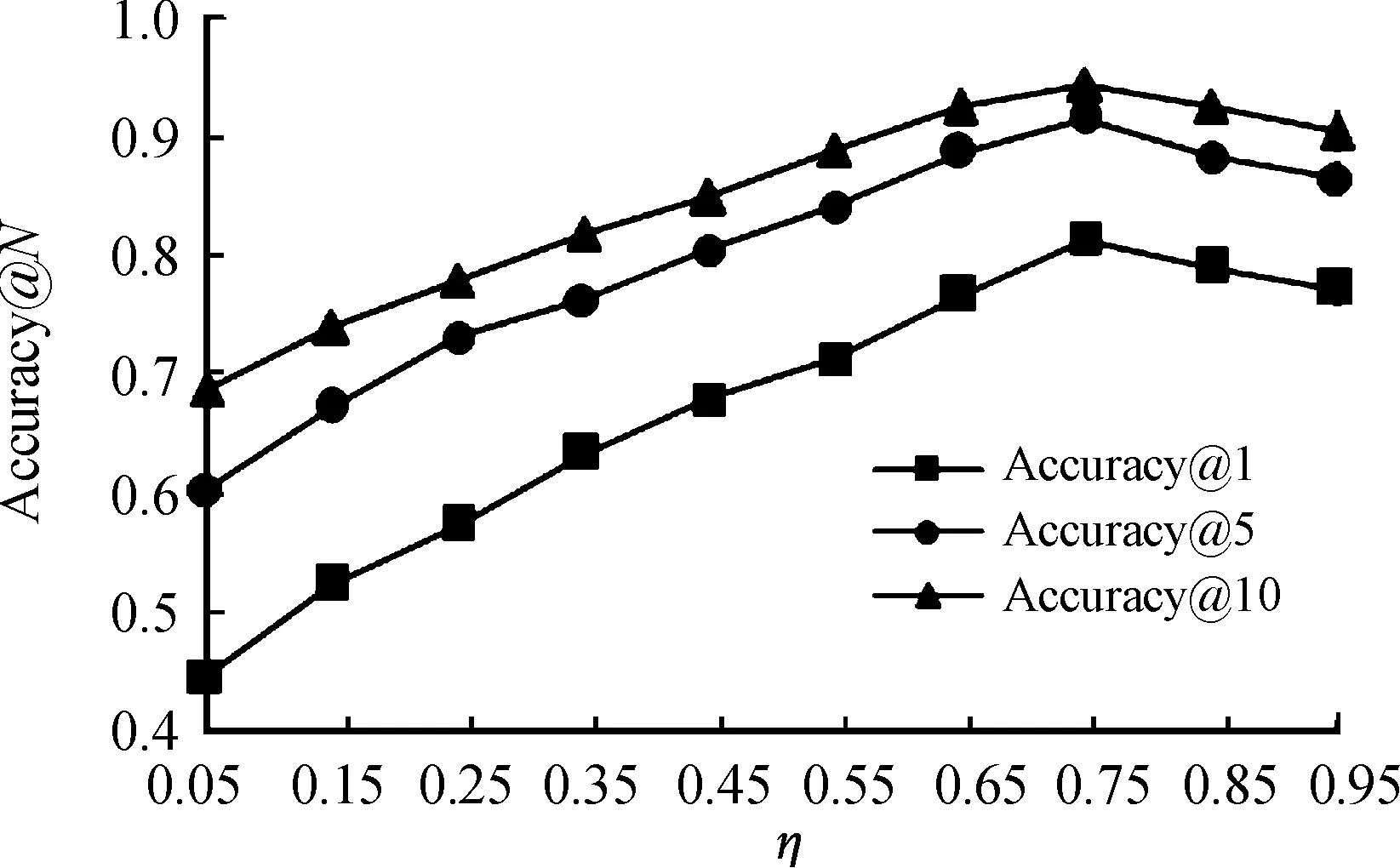
图6 不同η值下的预测准确性
此外,从图6中可以看出,用户移动模式模块具有更高的权重,说明模型在预测中用户历史移动模式比信任关系的影响更大;当λ=0.95时,表明过度强调了信任圈的影响,导致预测的准确率最差,说明仅仅考虑信任关系是不足以来预测用户行为的。参数η用于控制用户历史移动模式模块的影响,将λ固定为0.25,以0.05为步长将参数η从0增加到1。
从图6中可以发现,当η=0.75时达到最高准确率,这表明直接访问模式对于挖掘用户的隐性移动模式有重要的影响。当η=0.15时预测的准确率较低但不为0,证实了考虑多元访问模式的必要性,即通常情况下用户的移动模式都属于直接访问,但因部分数据集缺失或其他因素导致未能充分挖掘该用户的移动行为,本文考虑潜在的多元访问模式有效弥补了这一缺陷。
对于用户的k阶信任关系,本文将k设置成一个可变的参数,分别把k的取值设置为从1~20变化。图7展示了在k的不同取值下预测准确率的变化,可以观察到随着k值的增加,FTM的性能在不同的top-N下减少。因此可以得出结论,信任关系的等级对用户的选择有显而易见的影响,信任等级越高造成的影响越大。
根据文献[23]可知,个体用户能与周围用户保持稳定的社会关系的理论上限值,即任何人的社交关系都存在上限值。对于用户的n度邻近关系,本文将n的取值设置为1~5,因为只有部分社会关系与用户真正保持紧密联系,其他社会关系对用户的影响几乎可以忽略不计[24]。如图8所示,FTM的性能随着参数n取值的增加而减少,这是因为过多的社会关系削弱了亲密朋友的影响力,从而降低了预测的准确率。
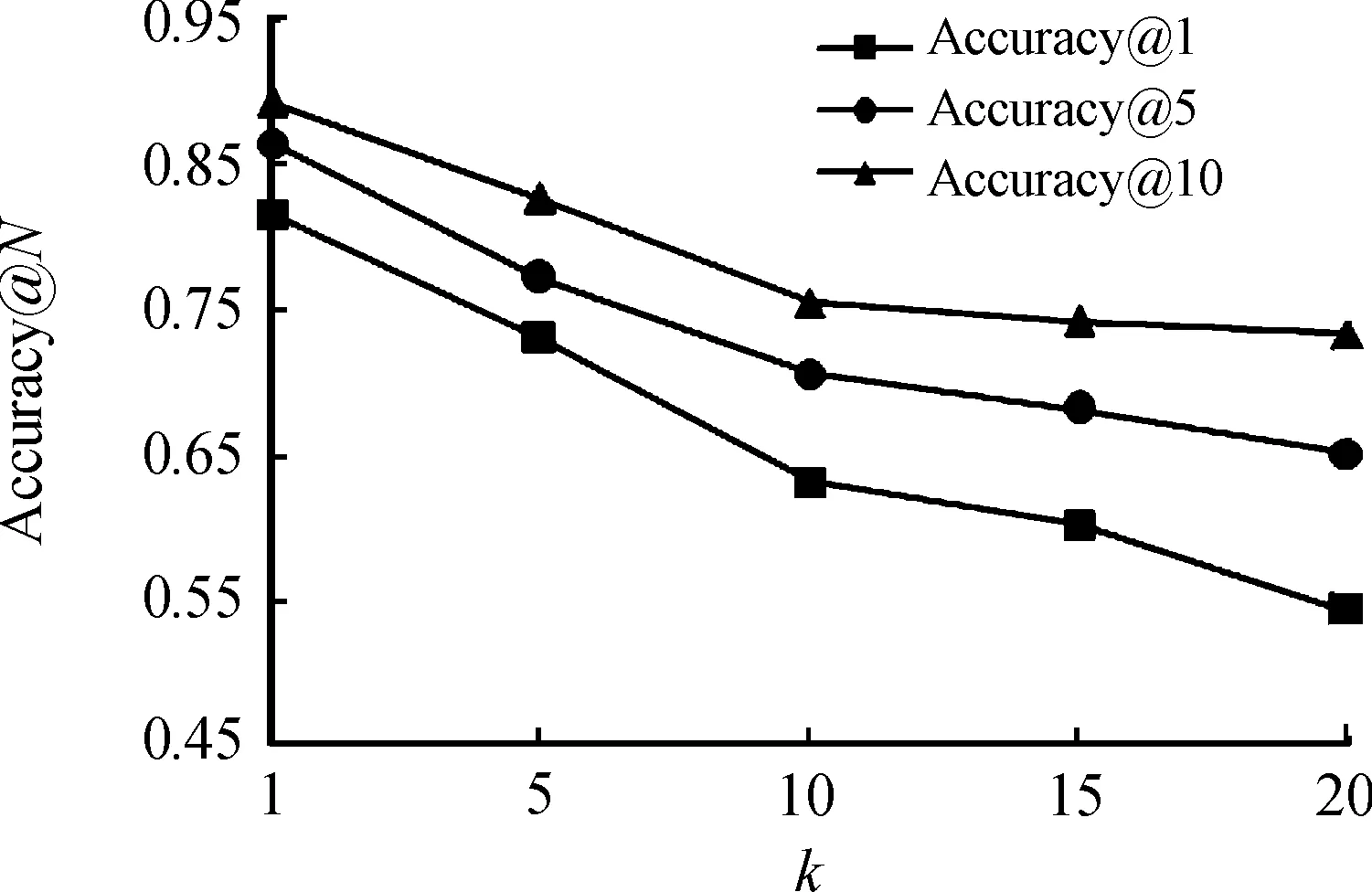
图7 不同k值下的预测准确性
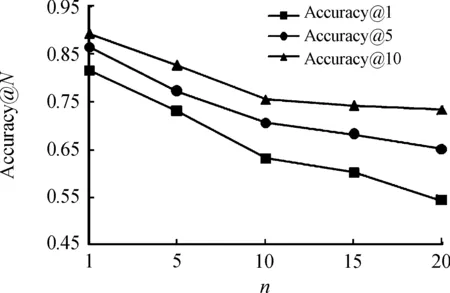
图8 不同n值下的预测准确性
3.6 位置预测准确性对比
表3展示了在不同数据集上的不同算法的预测准确率,可以看出FTM在所有模型中均表现最佳,平均准确率可以达到92.6%以上。
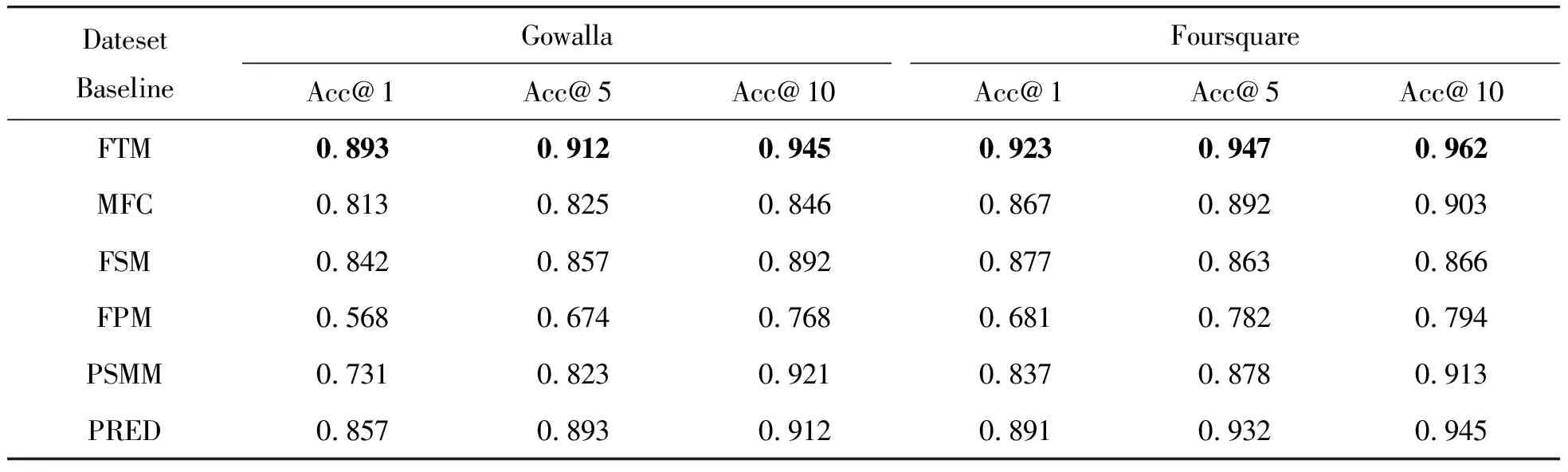
表3 实验结果
MFC模型虽然提供了较准确的预测,然而,考虑了用户的信任关系的FTM模型表现出更好的预测结果,尤其是在规模较大的Foursquare数据集上。FSM模型利用了描述用户运动模式的时空特征矩阵,但准确率相对较低,尤其是在数据集规模较小的Gowalla上。FSM模型比MFC模型的准确率高出约4.2%,但其准确率远低于FTM模型,原因在于仅考虑用户的局部特征。PSMM模型的准确率比FTM模型略差,因为其没有考虑信任圈对用户的影响,与FPM模型相比,它提高了大约20.6%的准确率。PRED模型综合考虑了地理信息和时间信息,也表现出较高的预测性能,但缺乏对用户个体的考虑,所以准确性较低于FTM模型。Gowalla和Foursquare这2个数据集的主要区别在于数据集的规模大小相差较大,所以在规模较小的数据集上,注重考虑局部信息的FPM模型准确率较高,在规模较大的数据集上,考虑多元信息的PRED模型准确率较高,而综合考虑社交元素和个体因素的FTM模型在不同规模的数据集上性能表现都是最佳的。
从图9可以更直观地发现:FTM模型的性能优于其他基准方法,这是因为FTM不仅考虑个体特有的移动模式,还考虑了多元社交信息的影响。具体来说,从图9(a)发现:由于Gowalla数据集规模较小,更多描述了用户个人特有的行为,而不能代表人群的通用习惯,对某些用户的信任圈的了解有限,导致FTM模型中的信任关系模块不能充分发挥作用,所以模型在Gowalla上表现的性能较低于在Foursquare上的性能。相反,从图9(b)发现:由于Foursquare数据集融合了更多描述人群规律的特征,适用于预测更广泛的用户群体行为规律[25],挖掘到的移动模式序列更具体,因此预测准确率更高。
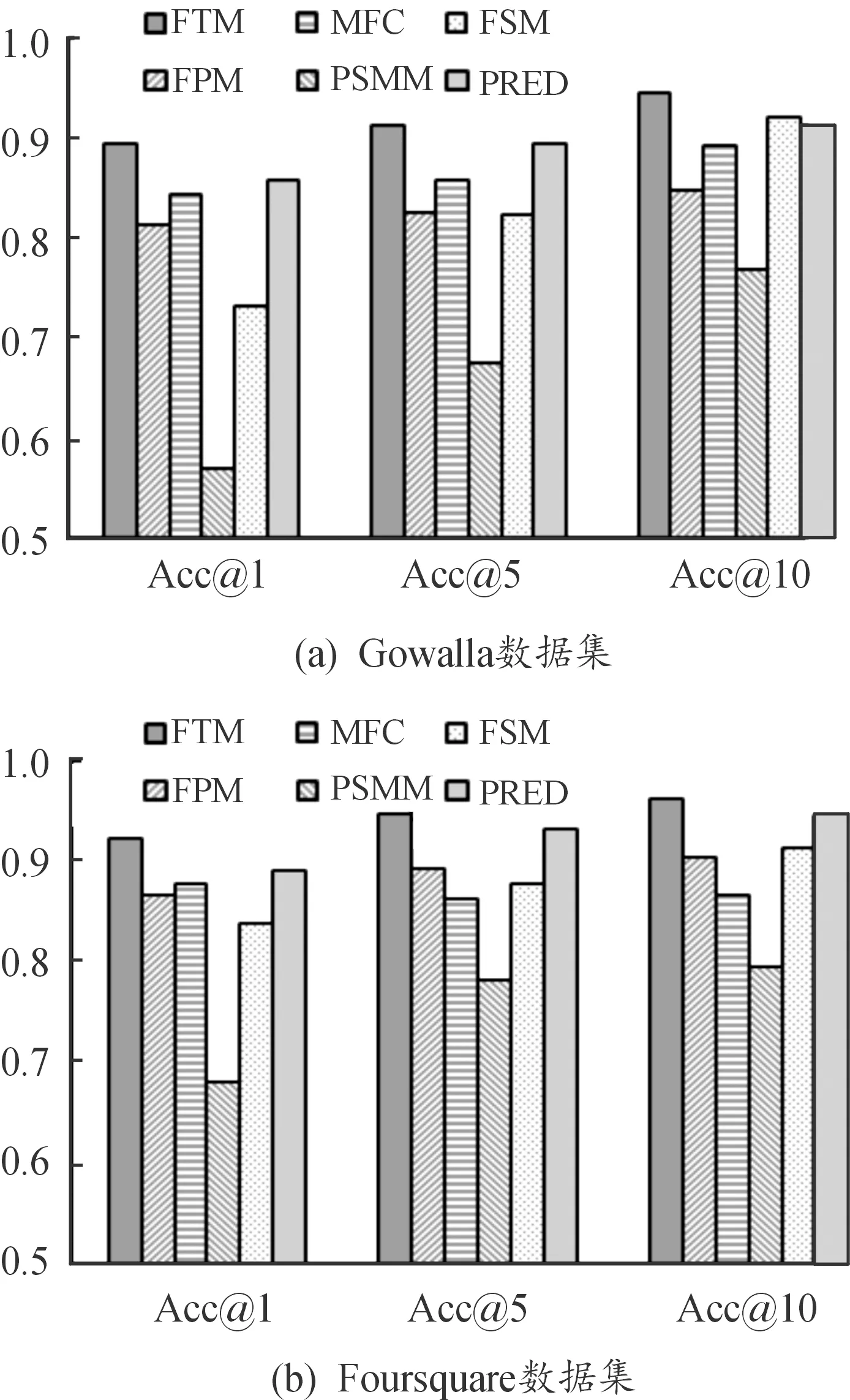
图9 位置预测率柱状图
本文进行了另一组实验来观察空间阈值变化对FTM性能的影响[26],将性能表现最好的Accuracy@10作为评价标准。
实验结果如图10所示,结果表明大部分模型的准确率随着空间阈值的增加而增加,FTM预测准确率明显优于其他算法的同时,表现出了更高的鲁棒性。

图10 不同空间阈值下算法的预测准确率曲线
从图10(a)可以发现,FTM模型和PRED模型的准确率增加的幅度更大,因为这2种算法都考虑多种影响因素,空间阈值的增大可以挖掘出更丰富的用户行为信息。相反,FPM和PSMM模型的准确率随着空间阈值增加而减少,这是因为仅考虑个体的单一影响因素存在局限性,这类算法更适用于预测特定个体的位置。从图10(b)可以发现,在Foursquare这种规模较大的数据集中,空间阈值的增大对预测准确率的影响更大,因为它允许在更多情境中预测下一个位置。FPM模型受阈值变化的影响尤其明显,与其他模型不同,该模型的准确率随着阈值的变化而减少,这是因为仅考虑局部因素导致的结果。同样,仅使用个体特征的PSMM模型表现不佳,因为该方法无法利用信任关系来弥补空间阈值变化导致的差距。结合图10可以发现,FTM模型、MFC模型以及FSM模型的准确率都随着空间阈值的增加而增加,而FTM模型的准确率是最高的,这是因为MFC模型考虑的影响因素较少,仅仅分析签到序列是不足以准确预测下一个签到位置的。FSM模型融入了直接竞争对手的概念,但是对其他社交关系的考虑颇为欠缺,导致预测的准确率较低于FTM模型。综合之前的实验,FTM在规模大的数据集Foursquare上预测准确率更高,因为用户的信息更丰富从而挖掘得到的线索越精确。
4 结论
本文提出了一种新的融合信任圈和移动模式的位置预测框架。在信任圈模块中,考虑了不同信任关系对用户选择的影响。在历史移动模式模块中,分别考虑了用户的直接访问模式和多元访问模式。在真实数据集上评估了不同模型的性能,实验结果表明,本文提出的FTM模型在准确率指标方面优于其他算法,并且较其他先进算法表现出更好的鲁棒性。未来工作包括:进一步拆分信任圈,从中挖掘其他社交关系对个体的影响并加入到预测模型中,并且在改进移动模式模块中挖掘用户多元移动模式的算法,进一步提高预测的准确性。
