回转支承局部故障动力学建模及仿真分析
2022-10-12江泽鹏王志伟段文军江志伟莫继良
江泽鹏,王志伟,段文军,江志伟,莫继良
(1.西南交通大学 机械工程学院,摩擦学研究所, 成都 610031;2.西南交通大学 盾构/TBM摩擦学设计实验室, 成都 610031;3.中铁高新工业股份有限公司, 北京 100070)
0 引言
盾构主轴承多采用三排滚柱式回转支承,是一种低速重载轴承,可同时承受轴向载荷、径向载荷及倾覆力矩[1]。作为盾构机等大型设备中关键的承载部件,回转支承受到了国内外学者的广泛关注。Göencz等[2]研究了3种典型滚子的几何形状对回转支承静载能力的影响。牛荣军等[3]分析了非对称接触角对四点接触球式回转支承的载荷分布、轴承刚度和承载能力的影响。潘星宇等[4]针对交叉滚柱式回转支承,得出了能够满足其使用寿命的最佳轴向载荷、径向工作游隙和最小油膜厚度。He等[5]针对单排四点接触球式回转支承的承载能力问题,对其滚珠数量和滚珠直径大小进行参数优化。蒋旭君[6]提出了回转支承接触载荷分布模型,并且分析了不同游隙对载荷分布的影响。冯建有等[7]基于非理想Hertz接触,研究了三排圆柱滚子回转支承中滚子与滚道间应力场的分布。王燕霜等[8]建立了负游隙下双排四点接触转盘轴承载荷分布计算模型,得出了轴承中最大接触载荷随负游隙变化情况。Zhang等[9]基于刚性套圈与柔性套圈,给出了风电机组回转支承的载荷分布,并对其结构参数提出了相关建议。李芃等[10]运用ANSYS/LS-DYNA建立了回转支承多体接触有限元模型,分析了回转支承运行时滚动体的动态响应。Zong等[11]基于Abaqus建立了回转支承滚道缺陷显示动力学模型,得到不同尺寸滚道缺陷下轴承振动响应。Lu等[12]将多个时域、频域指标组成特征向量,并结合概率主成分分析的方法实现了对回转支承寿命状态的特征提取。Pan等[13]将时域振动信号映射至圆域,并在此基础上提取特征向量,从而实现了对大型回转支承的早期故障诊断。Bao等[14]提出了基于流形学习和支持向量回归(SVR)的轴承寿命预测方法,并通过与其余优化算法的对比,验证了该方法的有效性。
综上所述,目前国内外对回转支承的研究主要集中在回转支承的承载能力、载荷分布,并对回转支承进行故障诊断与寿命预测等方面,对于回转支承动态特性研究较少,且多集中于轴承内外圈故障失效。然而,在盾构主轴承所使用的三排滚柱式回转支承中,由于承受载荷特别大,滚动体所承受应力较大,滚动体易出现划痕、剥落等损伤。当滚动体出现局部故障或失效时,很难通过检测手段进行有效测试,且将威胁盾构机服役安全。为了揭示服役过程中盾构主轴承特别是滚子划痕损伤下的动态行为,本文以缩比的盾构主轴承即三排滚柱式回转支承为研究对象,构建主推力滚子轴承动力学模型,探究健康/故障滚子运动过程中动态特性差异;并且进一步揭示了轴承转速、轴向载荷对故障滚子应力大小的影响。这将为盾构主轴承的研究设计与运营维护提供理论支撑与实际参考。
1 试验台简介
为模拟盾构主轴承服役过程中的受载情况,基于其结构特性与工作原理,团队利用缩比实验原理搭建了盾构主轴承损伤模拟试验台,如图1所示。主要包括基座、驱动电机、传动系统、液压加载系统与待测回转支承等,其中,回转支承安装于轴承座内。

图1 回转支承实物及损伤模拟试验台
实验装置运行时,电机通过齿轮传动系统驱动回转支承转动。液压加载装置可根据需要施加相应的轴向力、径向力及倾覆力矩。试验台具体技术参数如表1所示。

表1 损伤模拟试验台相关技术参数
在运行过程中,盾构主轴承同时承受轴向载荷、径向载荷及倾覆力矩,因而多采用三排滚柱式回转支承。考虑试验场地条件和结构尺寸的合理性,团队基于轴承结构(均为圆柱滚子且相同类型保持架等)及功能(承载工况及特性)一致性原则,使用缩比实验的方法进行相关研究。结合目前回转支承的国标型号,选用国标GB/T2300—2011中型号为133.25.500的三排滚柱式回转支承作为盾构主轴承的缩比研究模型[15]。该类型回转支承与实际盾构主轴承几何结构相同、功能类似,且能同时承受与实际盾构主轴承服役过程中的多种复合载荷。因此,选取作为盾构主轴承的缩比研究模型。
与实际盾构主轴承类似,该回转支承主要由外圈、内齿圈、三排滚动体及其保持架组成。其中,三排滚动体分别为:主推力滚动体、次推力滚动体和径向滚动体。其中,主推力滚动体和次推力主要承受轴向力及倾覆力矩,是回转支承的主要承载部分。径向滚动体主要用于承受径向载荷。在回转支承运行过程中,电机通过齿轮驱动内齿圈低速运转,进而带动三排滚动体与保持架绕内齿圈中心旋转。该型号回转支承内部结构如图2所示。
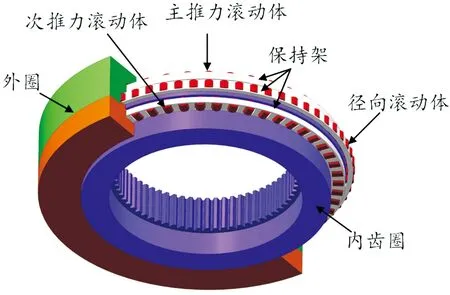
图2 三排滚柱式回转支承内部结构
其中,所选回转支承与参照盾构主轴承几何结构参数与工况参数如表2所示[1]。
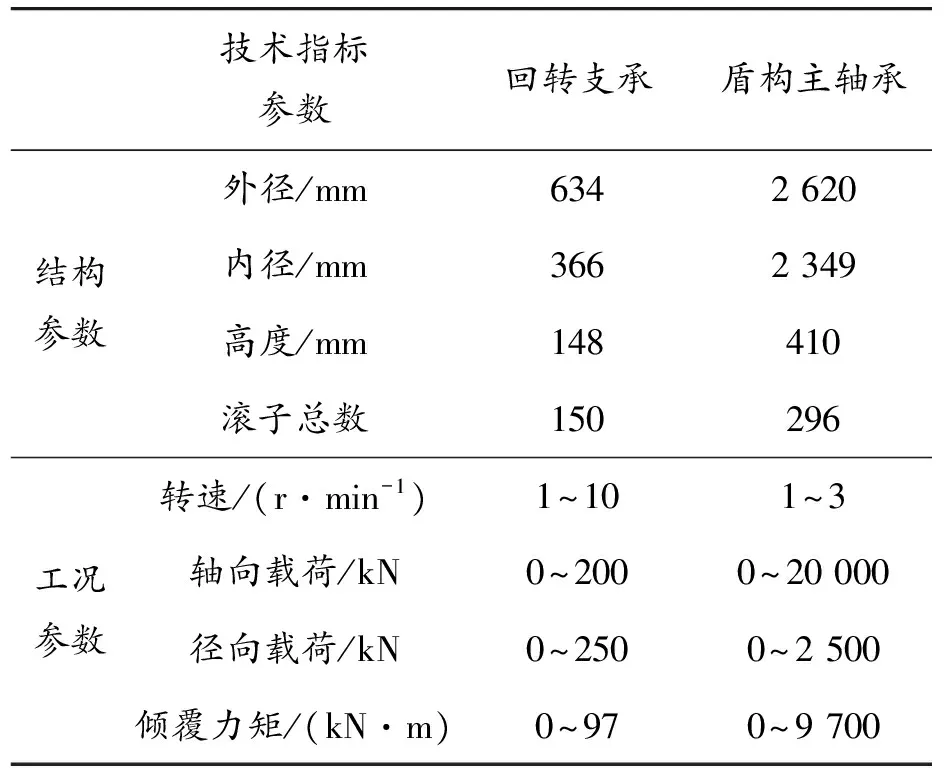
表2 所选回转支承与参照盾构主轴承
2 模型的建立
2.1 健康滚子动力学模型
三排滚柱式回转支承内部结构复杂,关键零部件繁多,而主轴承服役过程中受载最大的滚动体为主推力滚动体,是最易出现失效且影响最为严重的关键零部件。因此,本文仅关注回转支承中主推力轴承,并构建了相应的动力学模型,具体参数见表3。

表3 主推力轴承主要几何参数
在回转支承的主推力滚子轴承动力学模型中,去除了回转支承内部结构中径向滚动体与次推力滚动体等零部件,仅考虑了轴承内外圈、主推力滚动体及其保持架。其中,保持架可以随着轴承内圈的旋转而绕轴承中心公转,滚动体可以在绕轴承中心公转的同时绕自身轴线自转,具体有限元模型如图3所示。
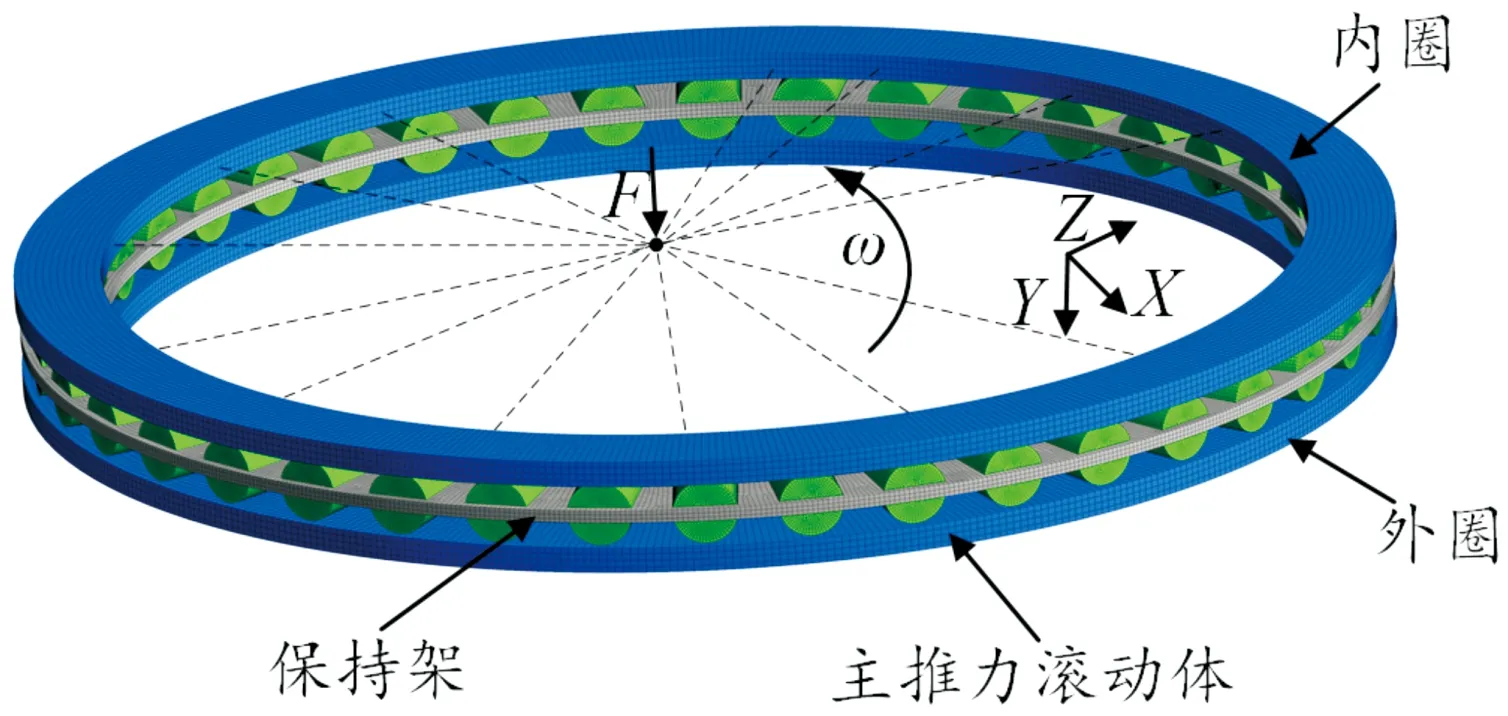
图3 健康滚子有限元模型
动力学模型中,定义外圈、主推力滚子的材料为线弹性材料。该回转支承外圈材料为50 Mn,密度为7 850 kg/m3,弹性模量为206 GPa,泊松比为0.3;该回转支承主推力滚子材料为GCr15,密度为7 800 kg/m3,弹性模量为210 GPa,泊松比为0.3。本文主要关注回转支承中滚动体与外圈接触状态且回转支承中保持架变形量极小,为提高计算效率,保持架和内圈被考虑为刚体[16-17],在ANSYS Workbench中,使用LS-DYNA模块建立上述有限元模型,使用显示积分算法进行计算。综合考虑计算精度与计算速度,采用8节点6面体单元,合理控制各零部件网格细化程度,最终整个有限元分析模型共有369 079个单元,432 666个节点。
2.2 接触、边界条件及工况
服役过程中,轴承不同滚动体分别与内圈、外圈和保持架接触,且保持架与外圈或内圈也有可能接触。因此,在动力学模型中,由于滚子数量众多且接触行为复杂,各零部件之间相互作用的设置是动力学准确求解的关键点之一。滚动体与内、外圈滚道表面的接触设置为面面接触,摩擦接触基于库仑公式,静摩擦因数设置为0.1,动摩擦因数设置为0.05[10]。在该模型中,共有80对接触对。由于滚动体与保持架间存在间隙,二者之间的接触存在不确定性,且保持架质量较小,其接触状态对结果影响较小,接触方式设置为无摩擦接触。
根据回转支承的安装及运行工况,对模型进行如下约束:回转支承一般与固定轴承座联接,约束其外圈外表面的6个自由度。限制保持架所有节点的绕X、Y、Z方向的平动和绕X、Z轴的转动,仅放开保持架绕Y轴方向的转动。同时,放开内圈绕Y轴的转动自由度。根据实际工况,对内圈外表面添加均布载荷,共30 kN的轴向力,设置内圈转速为10 rad/s。此外,为了减小轴承初始运转的不稳定性,同时为避免突加载荷引起的系统振荡干扰轴承的正常运转,本文先线性施加轴向载荷,待0.001 s载荷稳定后再线性施加转速。载荷、内圈转速具体加载情况如图4所示。
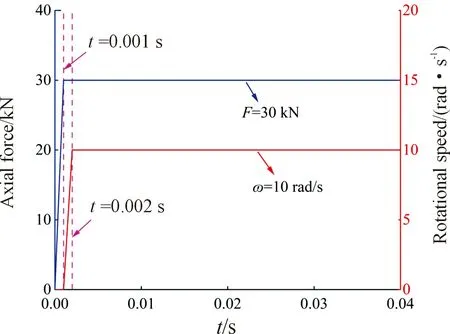
图4 轴承转速及轴向载荷加载曲线
2.3 故障滚子动力学模型
为更好地模拟真实情况下主推力滚动体故障类型,本文采用经典的圆周矩形来模拟出现在主推力滚动体上的划痕故障[18],如图5 (a)所示。其中,主推力滚动体直径D=25 mm,高度H=25 mm,矩形通槽的宽度d为1 mm,深度h为1 mm。在上述健康的主推力轴承动力学模型基础上,将所预制的故障滚子代替一个健康滚子,其余所有设置均保持不变,即可得到回转支承故障滚子动力学模型,如图5(b)所示。
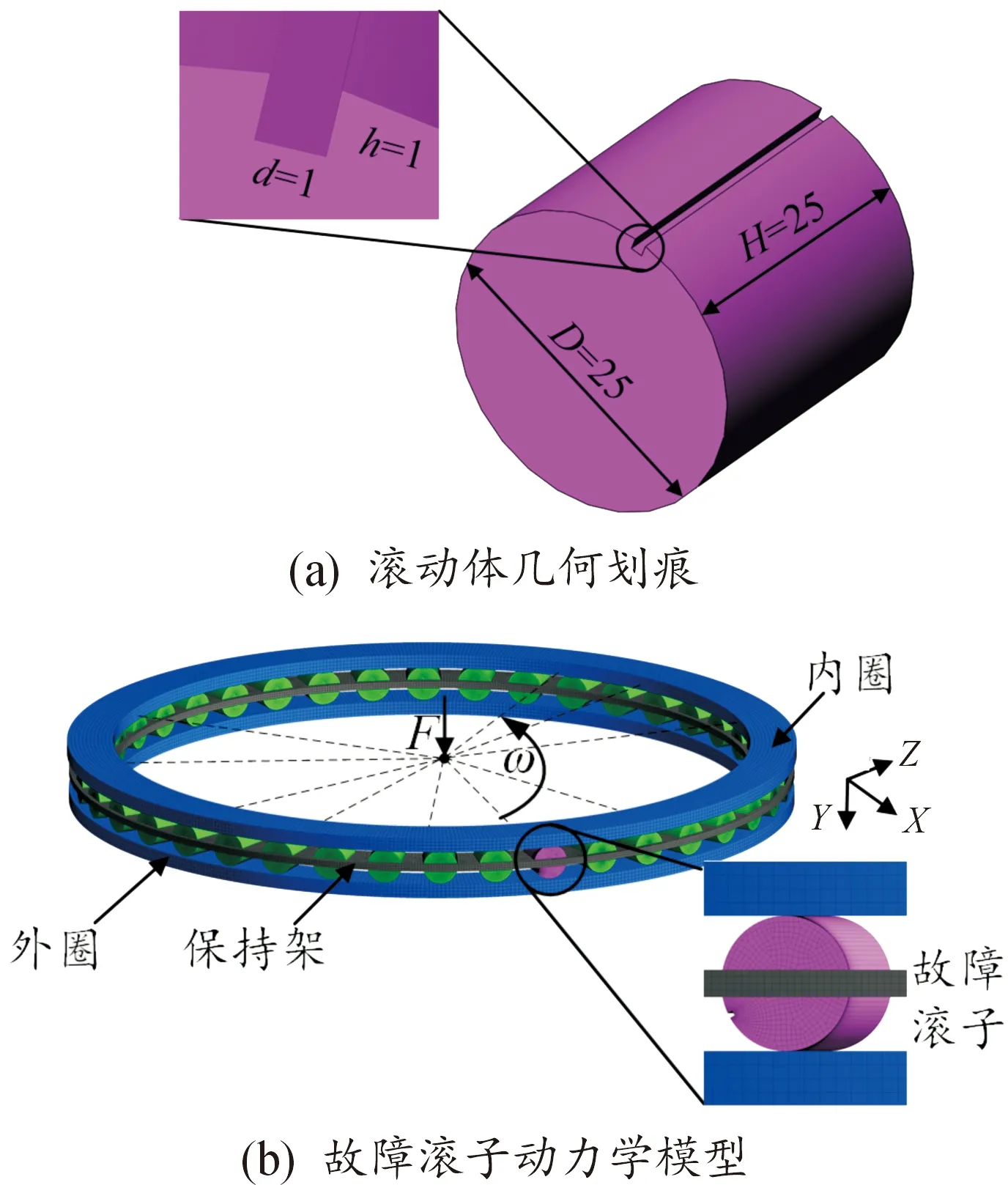
图5 故障滚子几何划痕及有限元模型
3 模型验证
3.1 保持架转速对比
在回转支承中,保持架绕着轴承中心公转。根据滚动轴承运动学可知,保持架理论转速为[19]:
(1)
式中:ωc为保持架理论转速,ωi为轴承内圈转速,d为滚子直径,D为轴承节圆直径,α为滚子接触角。当轴承内圈转速ωi为10 rad/s时,保持架理论转速为5 rad/s;提取动力学模型中保持架转速时程曲线,对比保持架理论转速与仿真转速,结果如图6所示。由图6可知,保持架仿真转速在初始加载阶段为零,随后保持架转速逐渐上升,最终在理论转速上下波动,与理论转速吻合较好。通过保持架理论转速与保持架仿真转速的对比,验证了本文模型的有效性。
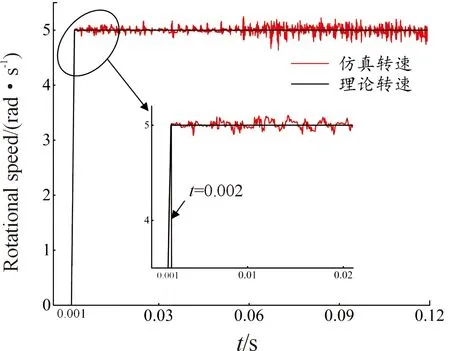
图6 仿真转速与理论转速曲线
3.2 实验验证
3.2.1实验过程
实验过程中,设定回转支承转速3 r/min,并向回转支承施加30 kN的轴向载荷。通过安装在轴承座端面上的三向加速度传感器,如图7所示,采集轴承运行中的振动加速度信号,其中,采样频率设定为2 kHz。

图7 振动加速度测点
3.2.2滚子滚过外圈固定点频率
在回转支承中,主推力滚动体在不断滚动的同时也在绕着轴承中心公转,在不考虑滚动体与内外圈相对滑动的情况下,根据轴承运动学可知,滚子滚过外圈固定一点的频率为[19]:
(2)
式中:fo为滚子滚过外圈固定点频率,fi为轴承内圈转动频率,Z为滚子数量,d为滚子直径,D为轴承节圆直径,α为滚子接触角。当内圈转速为3 r/min时,滚子经过外圈固定点的频率fo为1.0 Hz。选取主推力滚子动力学模型中某一外圈节点O,具体位置如图8所示,提取该点的振动加速度信号。
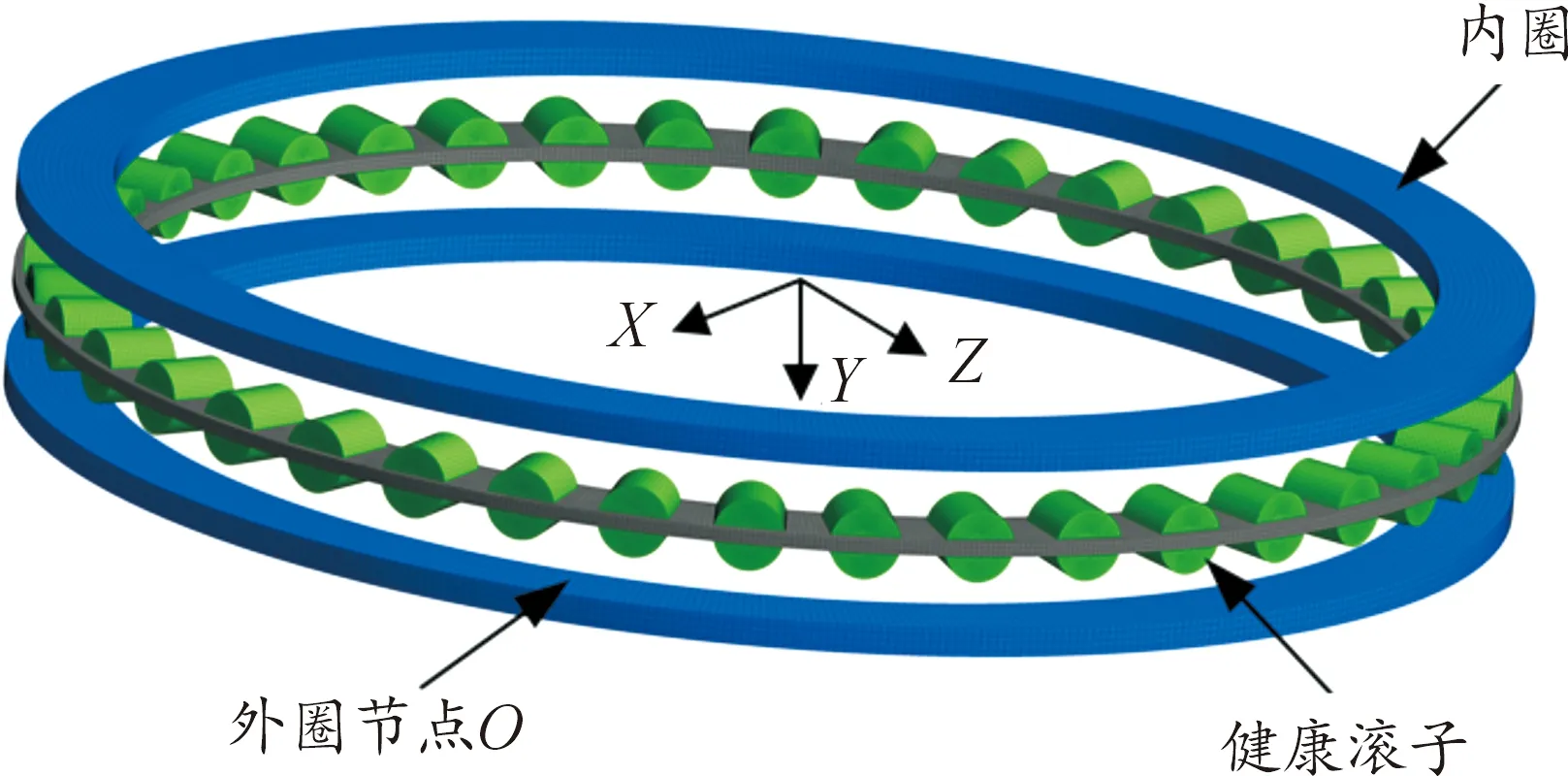
图8 外圈节点O的选取
3.2.3振动信号对比
将动力学模型中O点振动加速度与实验所采集的振动加速度信号进行包络分析,对比二者加速度信号的包络谱,如图9所示。由图9可知,二者包络谱中,滚子滚过外圈固定点的频率及其倍频清晰可见,综上,仿真结果与实验结果吻合,验证了本文模型的有效性。
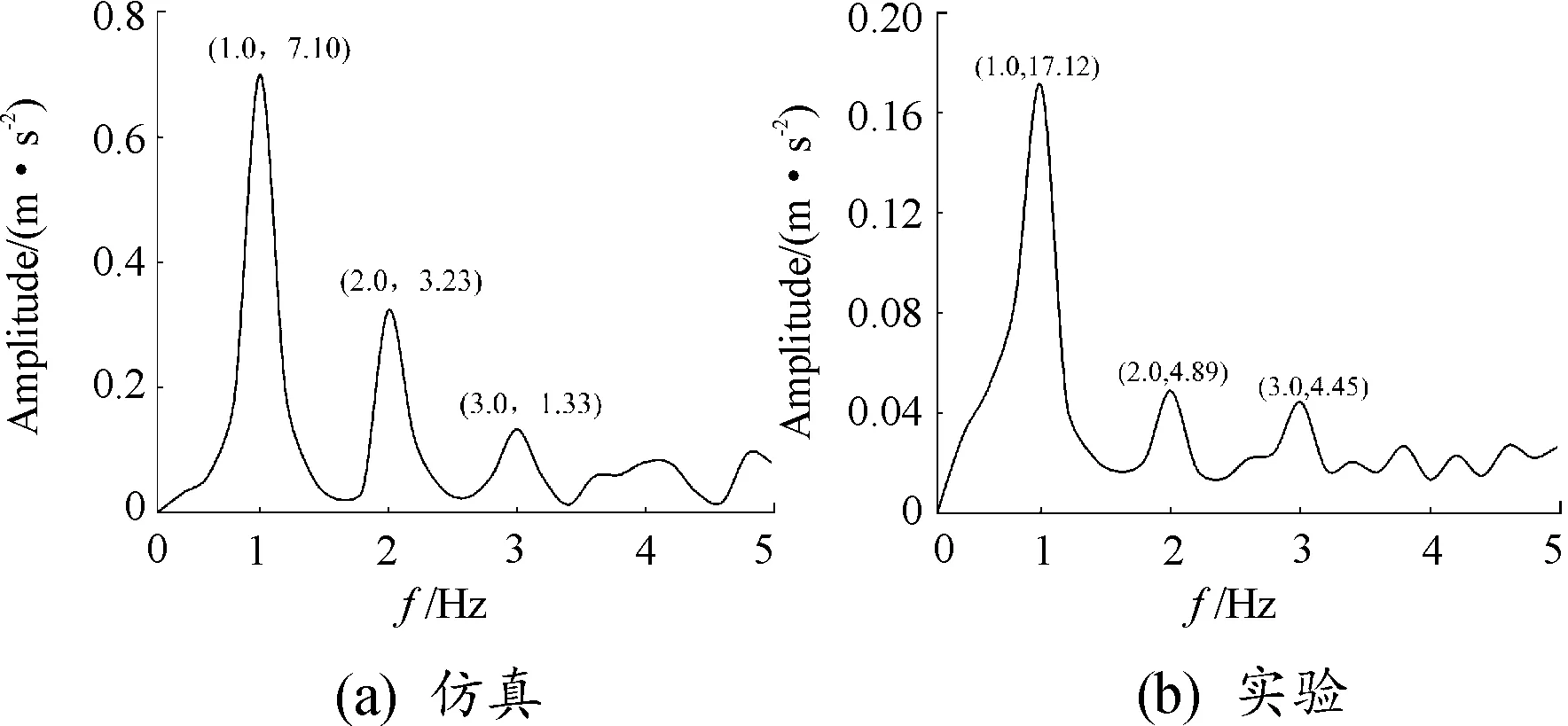
图9 加速度包络谱曲线
4 仿真结果与分析
4.1 滚动体动态应力对比
为探究几何划痕的出现对滚动体与外圈接触前后动态应力的影响,选取如下元素:① 对故障滚子,选取初始时刻故障区域边缘母线,沿母线上由内向外依次选取节点1-18,具体如图10(a)所示。② 对健康滚子,选取初始时刻与①几何位置相同母线,沿其母线上由内向外依次选取节点1-18,具体如图10(b)所示。
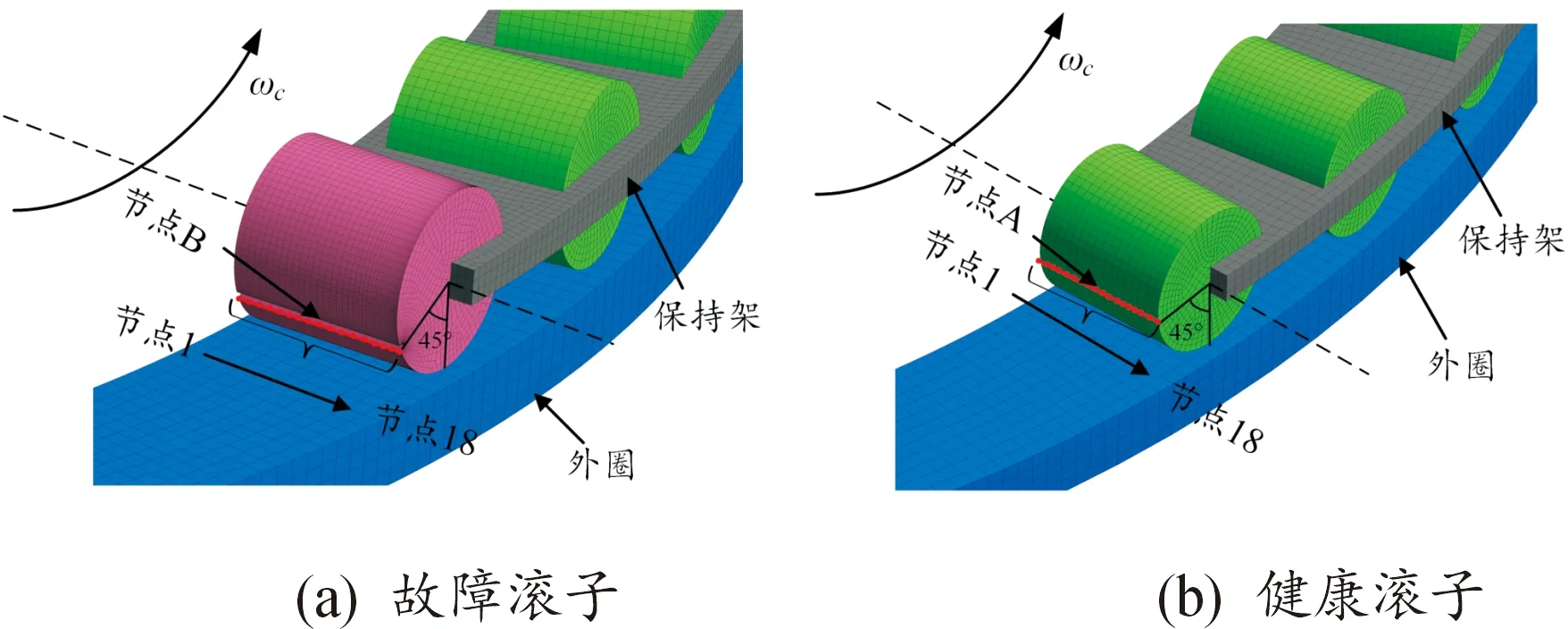
图10 滚子相关元素选取
4.1.1滚子接触外圈前后应力大小
动力学仿真过程中,轴承内圈转速为10 rad/s,轴向载荷为30 kN,仿真时间为0.12 s。选取仿真时间中0.074、0.076、0.078 s 3个时刻,分别对应所选节点接触外圈前、接触外圈时、接触外圈后的3个阶段。提取上述3个时刻滚子与外圈应力云图,并绘制所选节点平均应力时间历程曲线,结果如图11所示。图中α为所选母线和接触线分别与滚子中心连接的夹角。
由图11可知,在节点接触外圈前,滚子节点平均应力较小,随着滚子不断滚动,节点不断靠近外圈,节点平均应力不断增大,且故障滚子节点平均应力增涨幅度远大于健康滚子;在仿真时间为0.076 s时,节点与外圈接触,此时节点平均应力达到最大值,故障滚子与外圈出现应力集中现象,节点平均应力为1 428.98 MPa,远大于健康滚子节点平均应力108.01 MPa;随后,节点不断远离外圈,故障滚子节点平均应力以较快速度达到一个较小值,而健康滚子节点应力下降速度较为缓慢。
4.1.2滚子动态应力分布
为进一步探究滚子滚过外圈前后应力分布情况,选取健康/故障滚子节点1-18,如图10所示,对比健康/故障滚子接触外圈前后应力分布,结果如图12所示。
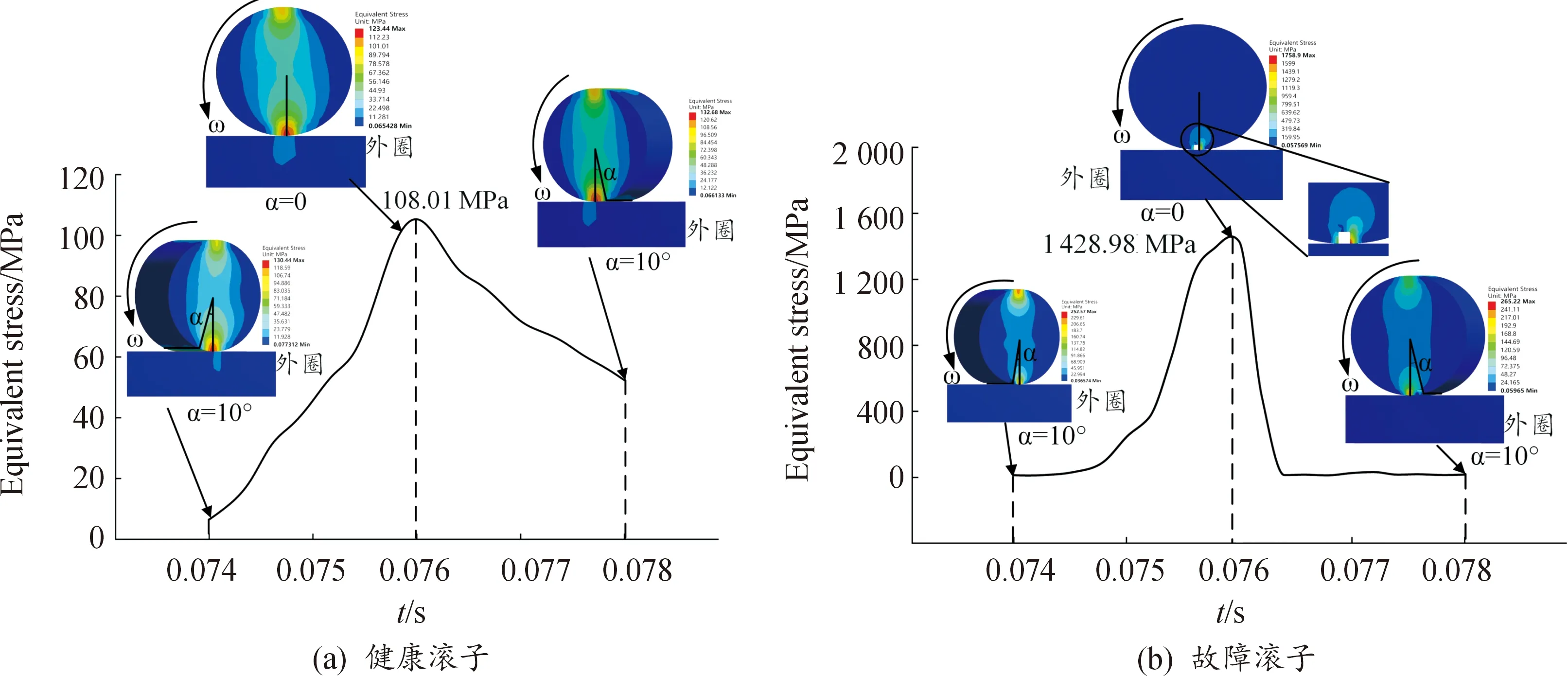
图11 滚子运动过程
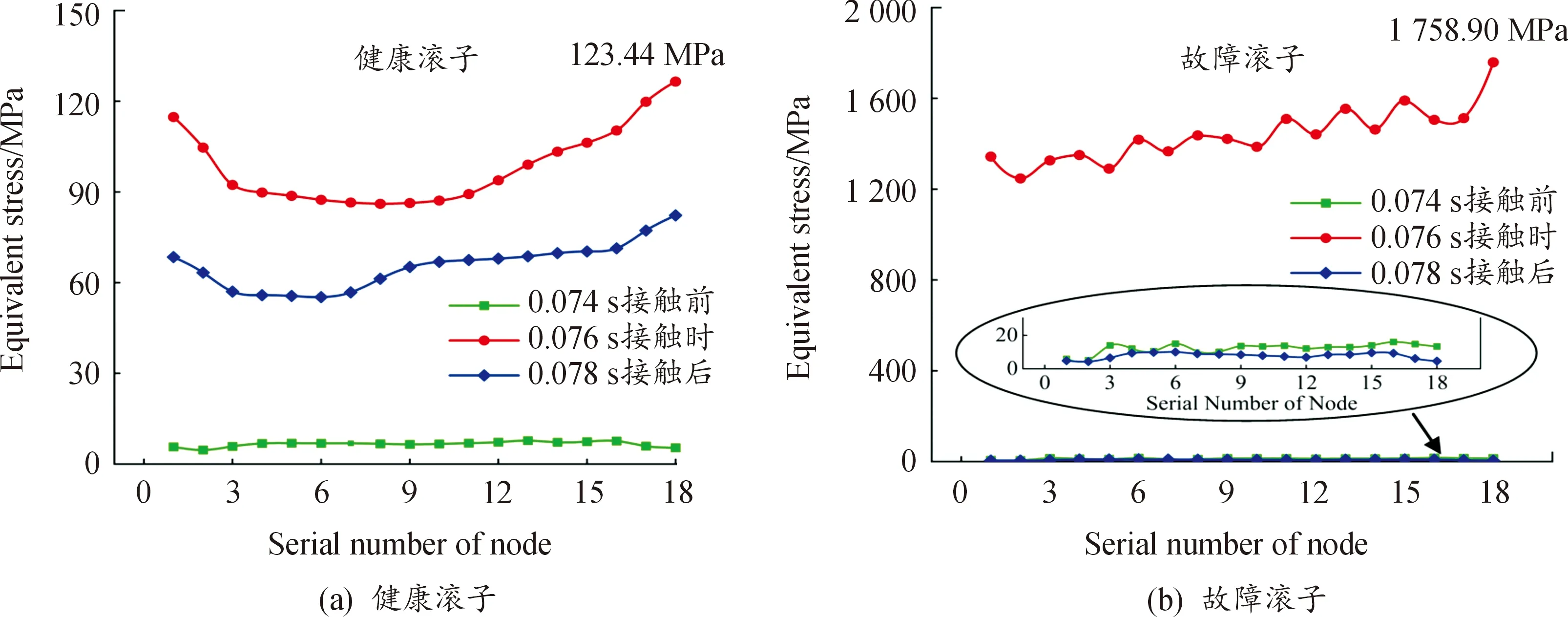
图12 滚子节点应力分布曲线
由图12可知,健康滚子在接触前,节点应力较小,应力在滚子轴向上分布较为均匀;接触时,节点应力增大,由于“边缘效应”的作用,应力呈现“两端大,中间小”的特点,即靠近滚子两端的节点应力大于滚子中心节点应力,且“两端”节点最大应力(123.44 MPa)比“中间”节点最小应力大了37.98%,这与回转支承滚子应力分布的相关研究一致[20];接触后,节点应力稍微减少,但仍呈现出与接触时相同的“两端大,中间小”的应力分布。故障滚子在接触前,节点应力较小,应力在滚子轴向上分布较为均匀;接触时,节点应力增大,节点应力呈现“外缘大,内缘小”的特点,即离轴承转动中心越远,应力越大,且“外缘”最大应力比“内缘”最小应力大41.31%;接触后,节点应力减少,应力沿滚子轴向上分布较为均匀。
4.2 轴向载荷与转速对应力影响
为探究轴向载荷与转速对健康/故障滚子运动过程中应力的影响,选取健康滚子节点A与故障滚子节点B,分析其在不同轴向载荷与不同转速下的应力变化,其中节点A、B均位于滚子轴向中点处,如图10所示。
4.2.1不同轴向力下滚子应力分析
基于前面建立的健康/故障主推力轴承动力学模型,分析不同轴向载荷下滚子应力变化情况。仿真中,内圈转速设置为10 rad/s,轴向载荷分别为10、20、30、40、50 kN。对比不同轴向力作用下节点A、B等效应力的变化,仿真时间均为0.12 s,具体工况如表4所示。

表4 不同轴向力工况
在回转支承健康/故障滚子动力学模型中,设置表4中工况1—5的各个参数,提取各自模型中节点A、B的等效应力,各工况下节点A、B等效应力时间历程曲线如图13所示。
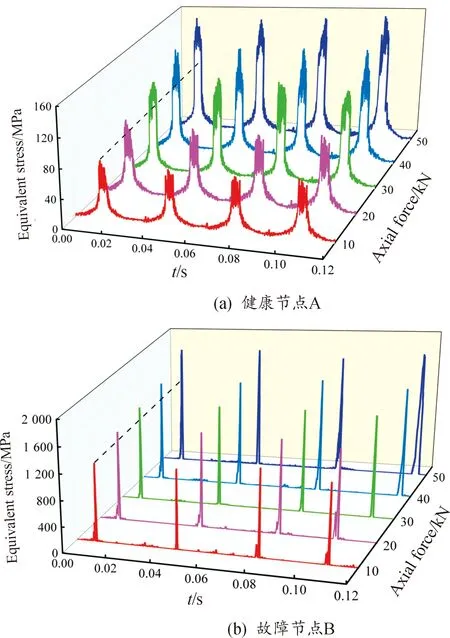
图13 不同轴向力下节点A、B等效应力时程曲线
由图13可知,在设定的仿真时间内,工况1—5下节点A、B等效应力随时间均呈周期性变化,均出现4次应力峰值,4次峰值时间间隔大致相等,且节点B应力峰值的升降速度比节点A更为迅速。结合前文可知,应力峰值出现在节点A、B与轴承内外圈接触时刻,且故障滚子节点B应力峰值远大于健康滚子节点A应力峰值,这是由于故障区域滚过内外圈时发生的应力集中导致的。随着轴向载荷的不断增加,节点A、B应力峰值都有明显上升趋势,计算工况1— 5下节点A、B平均应力峰值如图14所示。
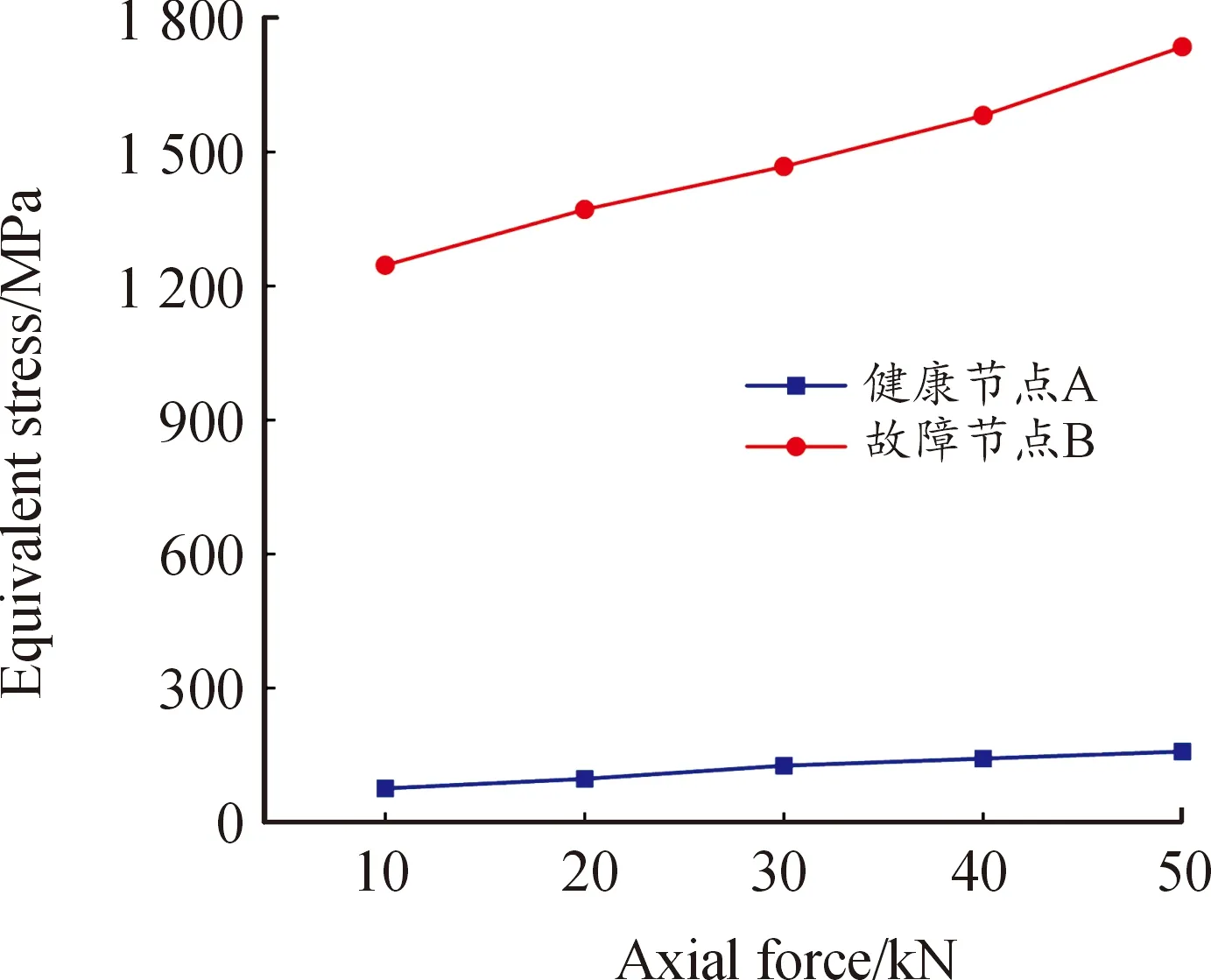
图14 不同轴向力下节点A、B平均应力峰值曲线
由图14可知,内圈转速一定的情况下,在轴向载荷为10~50 kN时,节点A、B的平均应力峰值随轴向力的增加而不断增加。对健康节点A,轴向力由10 kN增加至50 kN,其节点平均应力峰值增加109.14%;对故障节点B,轴向力由10 kN增加至50 kN,其节点平均应力峰值增加40.67%。
4.2.2不同转速下滚子应力分析
基于前面建立的健康/故障主推力轴承动力学模型,进一步分析不同转速对滚子动态应力影响。仿真过程中,轴向载荷设置为30 kN,轴承内圈转速分别为5、10、15、20、25 rad/s。对比不同转速下,节点A、B的等效应力随内圈转速变化。在保证节点A、B与内外圈分别接触2次的前提下,为提高计算效率,不同工况设定不同的仿真时间。具体工况如表5所示。
在回转支承健康/故障滚子动力学模型中,设置表 4中工况6—10的各个参数,提取各自模型中节点A、B的等效应力,结果如图15所示。

表5 不同转速工况
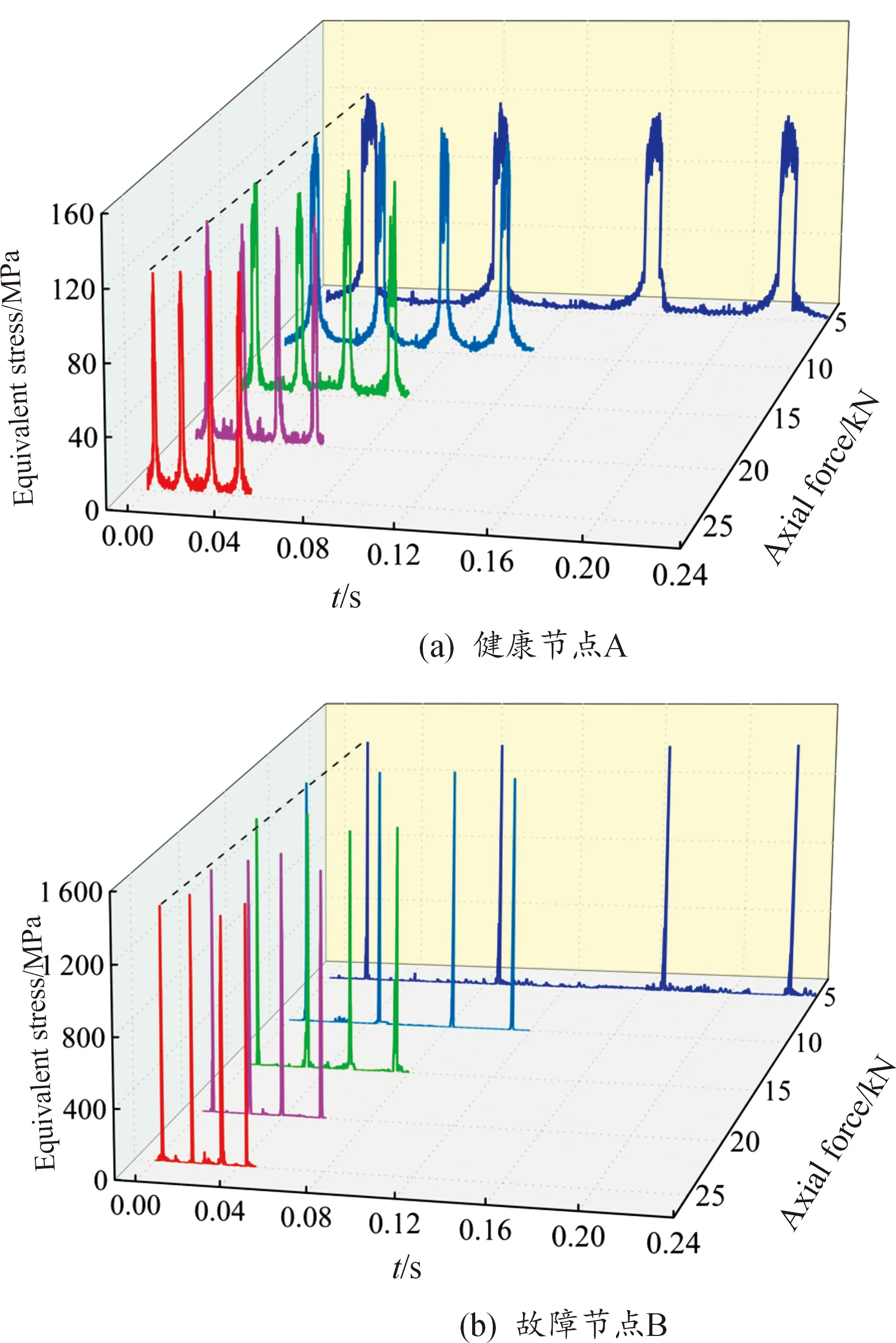
图15 不同转速下节点A、B等效应力时程曲线
由图15可知,在各自仿真时间内,工况6—10下对应的节点A、B均产生4次应力峰值,且4次峰值时间间隔随内圈转速增加而减少,这是由于随着内圈转速不断增加,滚子转频也不断增加导致的,而随着内圈转速增加,节点A、B应力峰值并无明显变化。计算工况6—10节点A、B平均应力峰值,如图16所示。
由图16可知,轴向载荷一定的情况下,在内圈转速为5~25 rad/s,内圈转速的变化对节点A、B平均应力峰值影响较小。
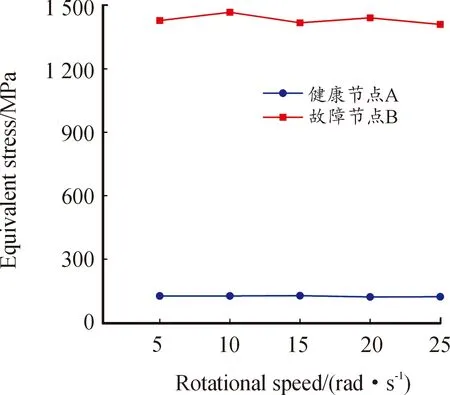
图16 不同转速下节点A、B平均应力峰值曲线
5 结论
1) 健康滚子和故障滚子与外圈接触时,接触线上分别呈现出“两端大,中间小”“外缘大,内缘小”的特点,且“两端”比“中间”节点应力大37.98%,“外缘”比“内缘”节点应力大41.31%。
2) 健康/故障滚子与外圈接触时,故障滚子接触线中点最大应力比健康滚子大14.25倍,且其变化速度比健康滚子更为迅速,可能进一步加剧滚子失效程度。
3) 内圈转速一定时,接触应力随轴向载荷增加而迅速增加。载荷由10 kN增加至50 kN时,健康滚子中心节点与外圈接触应力增加了109.14%,故障区域中心节点应力增加了40.67%。
4) 轴向载荷一定时,转速由5 rad/s增加至25 rad/s时,健康和故障滚子中心节点与外圈接触应力变化不明显。
