一种改进的内嵌式永磁同步电机虚拟信号注入MTPA控制
2022-10-12严晶铖曾成碧朱奇昊李佩霜邱仲睿
严晶铖,曾成碧,苗 虹,朱奇昊,李佩霜,邱仲睿
(四川大学 电气工程学院, 成都 610065)
0 引言
内嵌式永磁同步机(IPMSM)因结构简单、功率密度高、调速范围宽等优点被广泛应用于航空航天等领域。最大转矩电流比(maximum torque per ampere,MTPA)控制是在一定的输出转矩条件下,通过dq轴电流的合理分配降低定子电流及铜耗,提升电机转矩输出能力和系统效率,在IPMSM的控制中得到广泛关注。
精准的MTPA控制对参数依赖性极大,然而在不同工况下,受温度、磁饱和等因素的影响,IPMSM交直轴电感、磁链、电阻等均会发生非线性变化。如何降低MTPA对参数的依赖,从而减少因电机参数不确定而产生的的控制误差,是目前MTPA控制策略的一个研究热点。
为了克服电磁参数非线性的问题,目前的研究大体可以分为离线和在线的方案[1]。通过离线策略最常用的查表法,可得到电机参数或者最优电流参考值[2],但不具有普适性且需占据大量的存储空间。在线策略主要包括在线搜索法、代价函数法和信号注入法。搜索法通过向电流矢量角施加扰动在线搜索最优工作点,但其动态响应性能不佳[3]。代价函数法通过构建预测控制的代价函数,实现 MTPA 控制与模型预测控制的融合,但准确性无法得到保障[4]。信号注入法是向电机的电流或者电压注入高频的正弦、方波信号[5-7],对含高频扰动信号的响应信息进行调制,提取到正比于的信息,通过控制电流矢量角度,实时完成MTPA工作点的跟踪。但高频信号的注入会产生高频的转矩扰动并引入额外损耗,还可能会造成电磁干扰的影响。
考虑到上述的问题,文献[8]提出虚拟信号注入(virtual signals injection,VSI)的策略,不同于真实信号注入法,虚拟信号注入法对的提取是在虚拟转矩或虚拟功率模型上,由虚拟信号响应的计算得到。虚拟信号注入法具有对电机参数变化不敏感的特点,并克服了真实信号注入所产生的转矩脉动及损耗问题。为进一步提高虚拟信号注入法的控制精度,降低由于虚拟转矩或虚拟功率模型误差带来的控制偏差,文献[9]提出虚拟多信号注入的控制方法,引入了虚拟功率的概念,避开了滤波器的延时效应以提高控制系统的动态性能,但是虚拟功率算子对电磁参数的依赖性将降低MTPA控制的准确性。文献[10]提出向电流矢量角注入虚拟方波信号,依托转矩在当前矢量角度下的泰勒展开式建立了不依赖电磁参数的虚拟转矩模型,然而由于转矩是当前矢量角度的三角函数,对高阶偏导数的忽略会在一定程度上影响提取信息的准确性。文献[11]在2种虚拟信号注入法基础上,提出基于直流虚拟信号注入法的控制策略,但是该方法并没有考虑到虚拟电流注入对虚拟功率模型中电流幅值的改变所产生的误差。同时,针对系统在极值处波动的问题,文献[12]提出自适应的可调 振幅虚拟方波信号,从而得到波动较小的最优电流角度,但并提出相应阈值的理论依据。
本文中提出一种更加精准的虚拟直流信号注入法的MTPA控制,针对一般虚拟直流信号中虚拟功率模型产生的误差,定义了新的直流信号的注入准则,提高了MTPA判据的算法效率和精度。为验证虚拟直流信号的可行性,分析了系统在极值点附近的转矩振荡和局部稳定性问题,探讨了控制参数对MTPA控制性能的影响。通过理论分析和仿真实验验证本文提出的控制策略的有效性。
1 基于虚拟信号注入的MTPA控制
在正弦定子电流激励下,IPMSM在dq参考坐标系的数学模型中电压方程为
(1)
电机电磁转矩方程为
(2)
(3)
式中:vq和vd分别表示交直轴电压,电机的交直轴电感分别由Lq和Ld表示,永磁磁链为ψm。Lq,Ld和ψm随电机运行的工况变化而改变,可以将其视为id和iq函数。p为电机的极对数,ωm为电机转子转速。在dq参考轴下的电流幅值为Ia,电流矢量角为β。为满足电机在稳态运行下MTPA追踪,通过改变id和iq以达到最大电磁转矩的控制。
传统的虚拟直流信号注入法分别向交直轴注入直流信号,如图1所示。该方法忽略了电流幅值变化产生的误差,不同直流偏置的注入方法将产生不同的误差,这将导致∂Te/∂β的误差随电流矢量位置实时变化。考虑电流变化因素,∂Te/∂β表达式为:
(4)
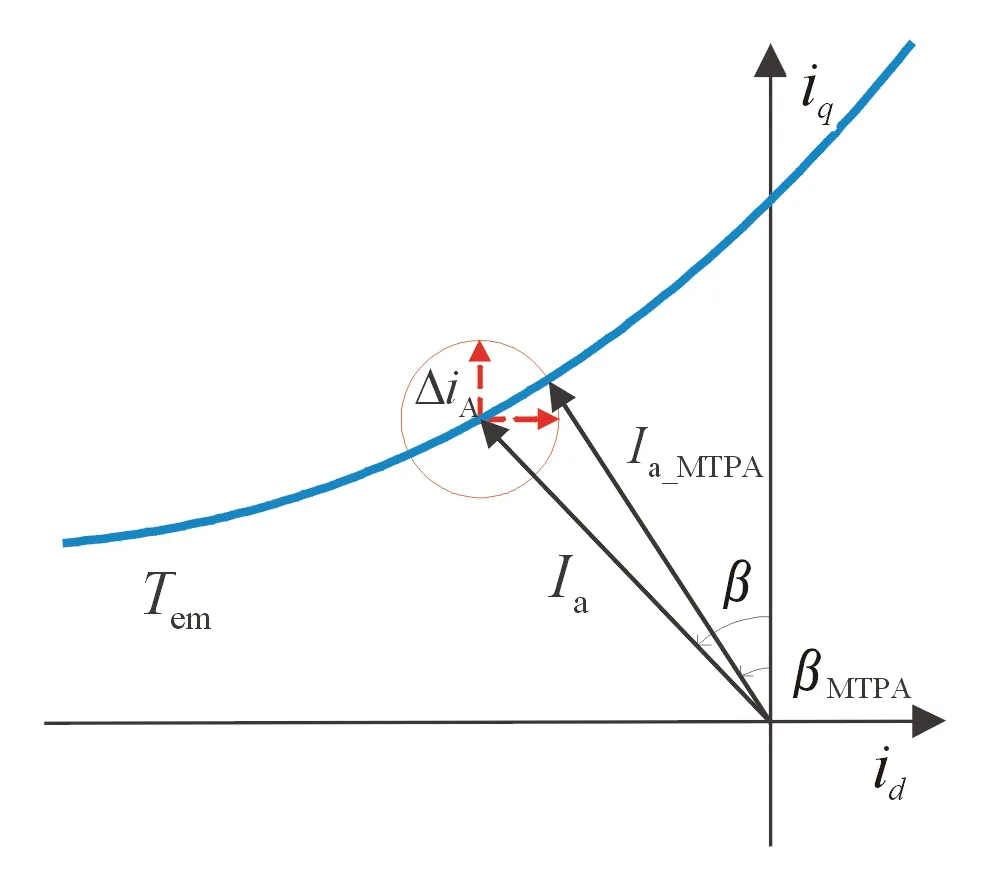
图1 传统虚拟直流信号注入法示意图
根据上述分析和电流矢量的关系,考虑电流矢量变化的影响,对任意的虚拟直流信号注入所产生的误差可以表示为:
(5)
传统的虚拟直流信号注入法中,∂Te/∂β是通过分别注入相同大小直流信号后合并计算的结果,因此无法保证在交直轴电流注入同样的电流偏置后∂id/∂Ia,∂iq/∂Ia偏导项与依据式(3)得到的偏导相互对应。在合理的直流电流A注入的情况下,传统方法MTPA的误差可以表示为
(6)
其中
(7)
式中:A表示注入的直流信号电流;ΔIa1表示单独向d轴电流注入直流偏置引起电流幅值的改变;ΔIa2表示单独向q轴电流注入直流偏置引起电流幅值的改变。通过上述分析,分别在交直轴注入直流信号方法将致使ΔIa1,ΔIa2随不同的id,iq变化而变化,ΔIa1≠ΔIa2导致该方案只能近似估计MTPA控制的误差。
2 自适应的虚拟直流信号注入法的MTPA控制
考虑到一般虚拟直流信号注入法产生MTPA控制的稳态误差,提出一种自适应的VSI控制策略,通过注入一个幅值恒定、角度动态变化的直流信号,求取不同工况下的MTPA下的∂Te/∂β,利用该导数项对id,iq进行控制,进而达到MTPA的控制目的。注入电流信号角度的最优选择实现自适应控制过程,优化∂Te/∂β计算效率,并保证MTPA的控制精度。
在利用式(4)求取偏导时,∂id/∂Ia, ∂iq/∂Ia对偏导的影响不大。而在实际运行过程中,电流幅值变化更多是受到采样信号的波动。由于直流信号所引起的电流幅值变化很小,导致对∂id/∂Ia, ∂iq/∂Ia进行估测增加了控制算法的复杂度,同时降低了准确性。因此提出最优的注入电流角度自适应律,角度应满足如下条件:
(8)
动态的注入信号可得
(9)
其中
(10)
式中,σ表示注入信号的角度。
图2为改进的虚拟直流信号注入示意图。当负载转矩保持不变,对于给定直轴电流参考值idref,交轴电流参考值iqref由此可以确定,因此对交直流电流的控制可以等效于改变电流矢量角度β。

图2 改进的虚拟直流信号注入示意图
(11)

图3 虚拟直流信号注入所对应转矩
当注入的电流幅值足够小时,转矩产生的变化分量中一阶项起到主导作用,因此在忽略高次项影响的情况下,得到
(12)
IPMSM的电磁转矩输出功率可以表示为
(13)
式中,ωe为电机的电角速度。
在虚拟直流信号注入法的基础上,根据式(12),交直轴电流的改变对应的虚拟的功率可以表示为
(14)
IPMSM中的永磁体磁链ψm、Ld、Lq都因为磁饱和效应而受到交直轴电流的影响,依据式(1),由电压稳态方程可推导出:
(15)
交直轴注入电流以后,产生的虚拟功率变化可以表示为
(16)
(17)
将式(16)和式(17)代入式(12)得到
(18)

虚拟信号注入法求取的偏导值通过积分环节得到idref,如图4所示。根据式(19),利用转速环得到的转矩参考值Tref得到iqref,再通过PI电流控制便可实现虚拟信号注入法的控制。
(19)

图4 虚拟直流信号注入MTPA控制框图
3 虚拟直流信号注入法的可行性分析
虚拟信号注入的MTPA控制自提出以后,研究主要集中于该方法的精度提升和适用范围,针对调制电压、控制方法存在的模型误差如何补偿[9-11,14-17]。目前的研究缺少对虚拟信号稳定性的分析,本节旨在从理论上论证虚拟直流信号注入法的可行性并分析不同设计参数选择对控制的影响,研究转矩在稳态下的振荡问题,分析系统参数在极值点附近的局部稳定性,并非提供一个全局性的稳定性证明。
在一个稳态时刻,可以将非线性速度控制环线性化,将电磁参数和机械参数视为常值。信号注入法的核心在于提取∂Te/∂β,并用于获取电流矢量角度或直轴电流参考值,2种获取方式因控制回路将造成电流幅值大小和交轴电流的滞后,但分析的方法是一致的。本文研究以获取直轴电流参考值为例,对于每个控制周期而言,将直轴电流参考值的获取过程视作为扰动信号Δid,通过系统控制回路改变Δiq,两者共同决定Δβ,根据本文的MTPA策略得到∂Te/∂β,并影响下一个控制周期的Δid,它们之间的关系如图5所示。

图5 系统状态变量与控制变量关系示意图
为简化虚拟信号注入产生的信号扰动的分析,假设:
1) 鉴于电流环回路的响应是远快于转速环,忽略电流控制和电流,电压采样的暂态影响;
2) 系统运行于稳态过程,此时合成电流矢量位于旋转坐标轴第二象限;
3) 利用稳态方程求解出的虚拟功率差与转矩关于交直轴电流的偏导项可以忽略;
4) 将扰动信号Δid看作以大小任意的控制周期变量,令Δid=Rsin(ωrt+φr)。
设在转矩最大的极值点附近存在工作点S0,该工作点的参数和状态集合见式(20)—(22)。同时建立控制回路的小扰动方程。
S0={id=id0,iq=iq0,Ia=Ia0,
β=β0,ωm=ωm0,TL=TL0,
Te0=Te(id0,iq0,ψm0,Ld0,Lq0)}
(20)
(21)
(22)
其中
(23)
式中:ΔTe、Δido、Δiqo、Δeω、Δx表示在系统平衡值的变化量;KPω和KIω表示速度PI控制器的比例和积分增益。由此建立小信号模型,如图6所示。

图6 控制回路的小信号模型结构示意图
可以推出关于扰动的传递函数为
(24)
其中
(25)
为简化分析,将系统的id0可以看作控制频率wr为基础频率的周期扰动信号。忽略控制周期对系统的相位的滞后的影响,令
(26)
结合式(24)—(26),得到
Δiq=kktkGΔid
(27)
iq与id的扰动可能会造成系统在稳定状态下的转矩振荡。为克服类似问题,控制电流矢量在iq与id的扰动下仍处于恒转矩电流工作区,由此可推得所期望的Δiqe为:
(28)
从式(27)可知,k和kt是由电机所处的运行工况决定的,而kG是由系统本身及其控制参数决定的。因此,通过对系统控制参数的修正,从控制理论上可避免系统稳态处转矩振荡问题。联立式(27)和式(28),可求得
(29)
由式(29)可知,不同转矩和转速所引起的电磁参数非线性变化,导致最优的系统增益kG也随之改变。因此在控制系统的设计过程中,可以通过自适应调节不断改变系统转速环的设定将稳态处的转矩变化控制在较小范围。 值得一提的是,真实信号注入是在电流上施加实际扰动,而本文分析的电流扰动是建立在控制环节本身,系统在稳态下的扰动程度取决于直轴电流参考的获取方式,因此虚拟信号注入法可以从根本解决在系统在稳定状态下转矩振荡问题。
为简化系统在极值处的局部稳定问题的分析,考虑到电机的转速与定子电流变化所产生交直轴电压变化是不显著的,可忽略其对∂Te/∂β提取的影响,由虚拟功率模型得到的∂Te/∂id和∂Te/∂iq是准确的,此时id的控制方法可以表示为:
(30)
同时,存在工作点S1满足
(31)
工作点S0与工作点S1之间的系统状态为本文局部稳定性分析的范围。单个控制周期内的Δid可表示为Δid=-kiλ,为使得Δid收敛于0,因确保对Δid的控制和Δiq的系统响应所引起的电流矢量角度的改变小于系统由工作点S0过渡到工作点S1的电流矢量角度变化,故Δid收敛于0的临界条件可表示为
Δid=Is0sinβs0-Is1sinβs1
(32)
联立式(31)和(32),建立电流矢量角的方程为
(33)
忽略极值点附近的电流变化情况,得到:
(34)
积分系数的取值是本文控制系统中Δid=0的关键。积分系数的选取应小于式(34)所提出的临界条件,因此虚拟信号幅值大小只决定了MTPA追踪精度,并不会影响系统的稳定性。同时,系统的负载变化也将改变积分系数的选取范围。文献[12]在积分因子乘上了虚拟信号幅值,因此注入信号的振幅会对电流矢量角度的稳态波动产生影响,但其方法本质也是通过调节积分系数去改善载荷变化下的稳定性能。
在满足上述条件时,系统存在平衡状态。当∂Te/∂β=0时,Δid=0。为进一步分析系统在极值附近的稳定性,建立李雅普诺夫方程:
(35)
根据式(3)(30)和(35),李氏函数关于时间的导数可以写为
(36)
dV/dδ与did/dt异号,由式(3)算得dβ/did恒小于0,同时转矩关于电流矢量的函数在工作区间时为凸函数,故dδ/dβ恒小于0,因此可得李氏函数的一阶导数为负数,故系统在极值处的平衡状态是在其邻域范围内是一致渐进稳定的。积分系数决定了每个控制周期Δid的大小。图7表示在∂Te/∂β=0的临近区间内不同积分系数对应的系统渐进稳定和不稳定2种情况,积分系数对MTPA控制的局部稳定性起到决定性作用。
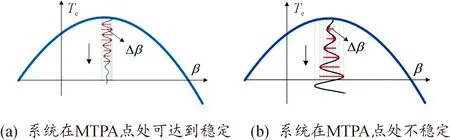
图7 系统局部稳定性判定示意图
4 仿真验证
为验证所提出虚拟信号注入法的MTPA控制策略的可行性,在Mtalab中搭建永磁电机控制仿真系统。首先验证该策略对MTPA工作点的追踪可靠性,同时通过对比虚拟正弦信号注入法与传统的虚拟直流信号法,验证其在变载运行的动态响应和准确性。仿真采用的电机参数如表1所示,虚拟直流信号幅值为0.01 A,幅值的选取决定了转矩偏导的准确性,并不会改变收敛到MTPA工作点的速度。
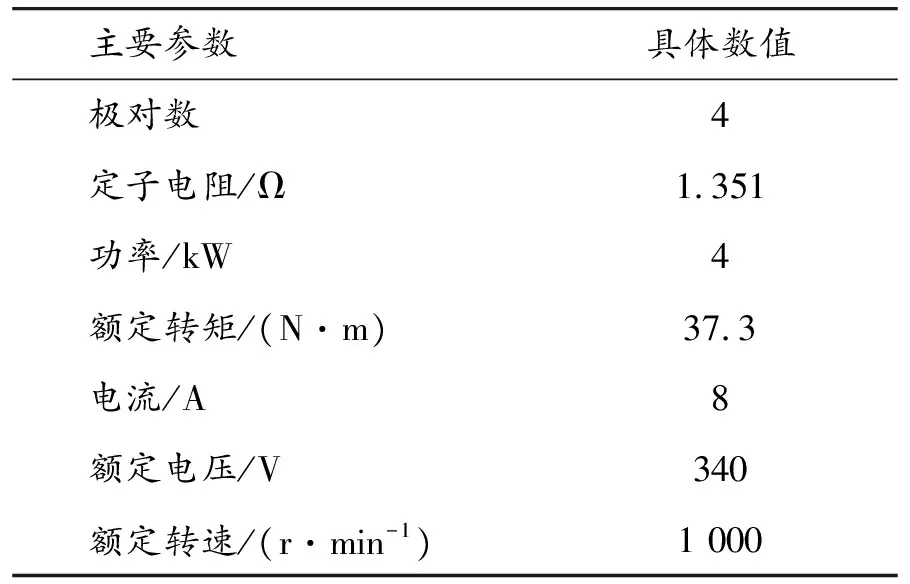
表1 内嵌式永磁电机参数
MTPA控制的有效性通过两方面进行验证。首先是id=0控制到虚拟信号注入法控制的切换运行,电机转速设定在1 000 r/min,负载转矩为25 N·m,在第4 s时切换为虚拟信号注入法,仿真结果如图8所示。此时电流幅值由5.54 A下降到5.40 A,对应的电流矢量角度为5.8°。
考虑到电机可能工作于频繁的变负载工况,因此在不同负载转矩工况下对虚拟信号注入法进行验证。电机在1 000 r/min的转速下,负载转矩的变化由5 N·m先逐步增加到30 N·m,然后再减少至10 N·m,此时的负载变化与定子电流响应如图9所示。
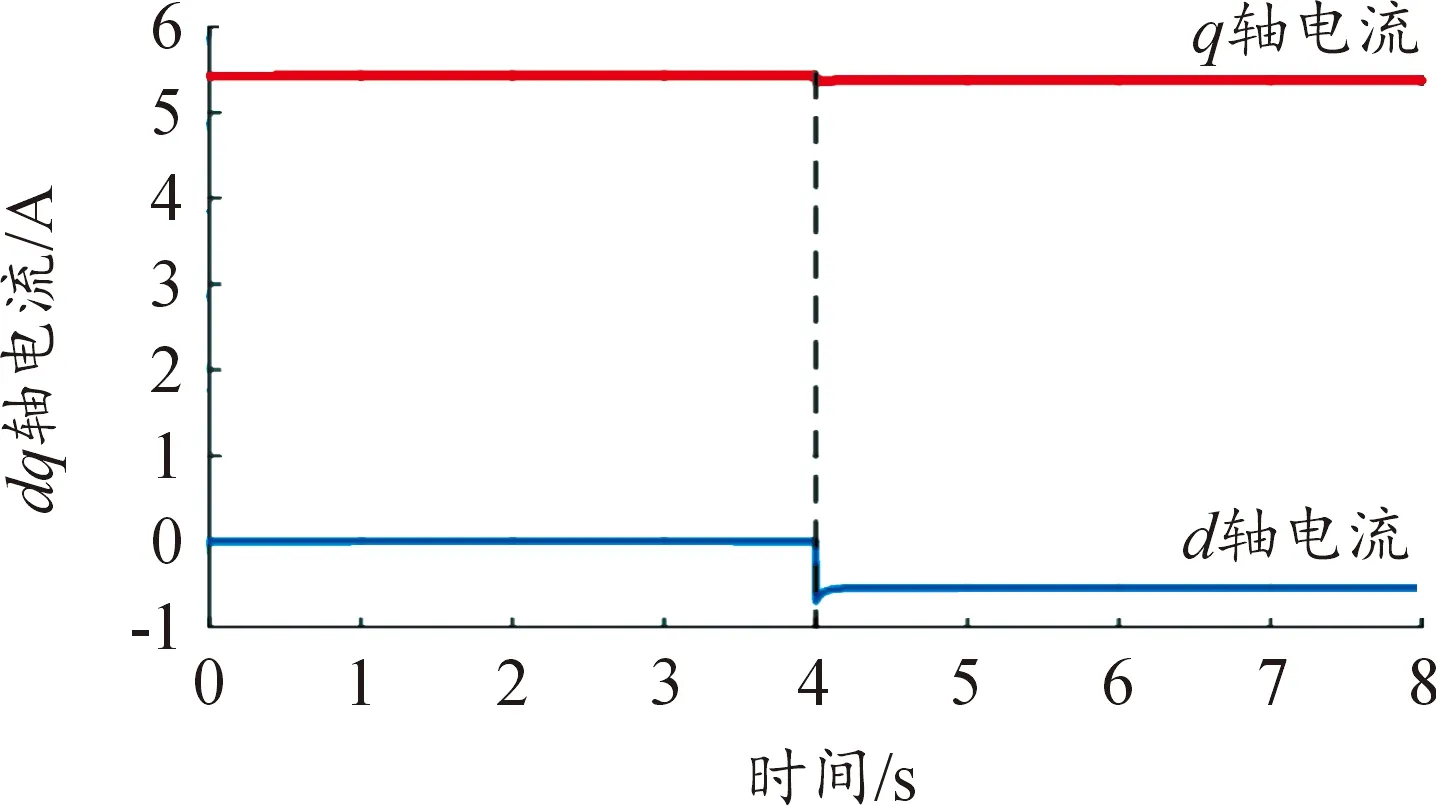
图8 由id=0切换至虚拟信号MTPA控制仿真结果
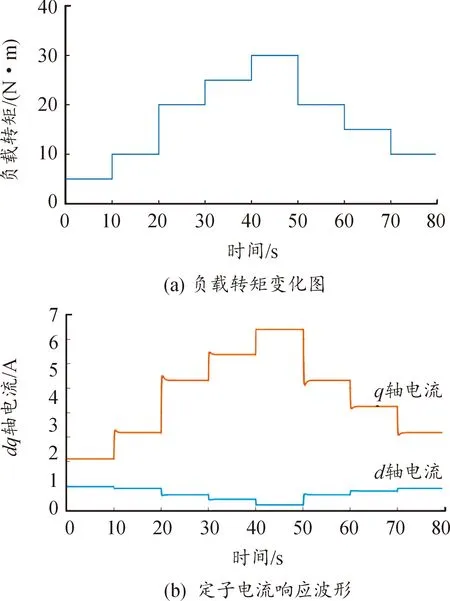
图9 电机变载运行的仿真波形
为测试所提出的MTPA控制策略的动态性能,将虚拟正弦信号注入法用于电机的控制,同时将速度环的PI参数以及决定直轴电流给定的积分器参数设置为一致,对比2种控制策略分别在负载转矩由15 N·m变化到25 N·m,再改变到20 N·m的动态响应,其结果如图10所示。分析结果可以得到,虚拟正弦信号法的控制策略由于MTPA判据依赖于带通滤波器与低通滤波器,直轴电流给定值需要11 s的时间才能达到稳定,而本文所提出的控制策略可以在1.5 s时达到稳定,具有更好的动态性能。
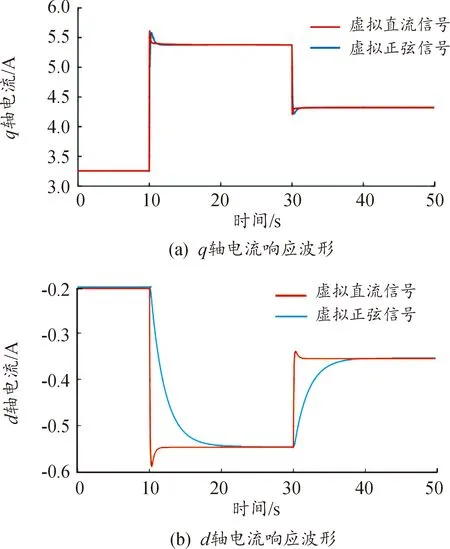
图10 虚拟正弦信号注入与虚拟直流信号注入控制波形
虚拟直流信号注入法的动态性能取决于积分器参数与电机工况。电机的工作条件不同将导致该时刻所提取的偏导系数不同,考虑到电机工况的不可控性与电机参数的交变的影响,积分器不仅在决定了控制的稳定性,同时也影响了控制的动态特性。改变积分器的系数,得到的id电流响应如图11所示,在不同的积分系数情况下,系统都能在2 s内达到稳定,同时可以得到最适合当下工况的参数设定。

图11 不同积分器设定的d轴电流响应
为验证本文的MTPA控制策略的准确性,将传统的虚拟直流信号注入法运用于本文采用的电机中,在变载的运行的稳态条件下,定量分析对应的定子电流,利用Hamilton插值的方法得到2种方案的MTPA轨迹,其结果如图12所示。为了定量分析传统虚拟直流信号注入法的理论误差,忽略电机电磁参数交变,根据式(8)推出系统在不同的直流分量与不同负载下的误差水平,结果如图13。MTPA的误差随着虚拟直流信号的增大而增大,负载转矩的越小误差水平越大。传统的虚拟直流信号与实际的MTPA在理论上存在细微的误差,而所提出的MTPA控制方法更加准确。
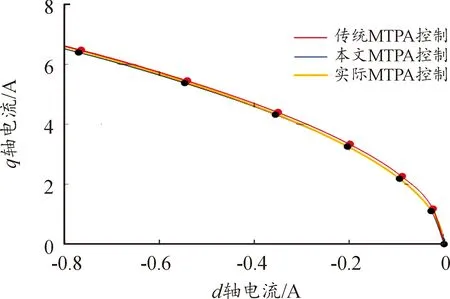
图12 虚拟信号注入法的MTPA控制轨迹

图13 传统虚拟直流信号∂Te/∂β误差结果
5 结论
针对IPMSM当前的虚拟信号注入法的MTPA控制存在的问题,提出了一种改进的虚拟直流信号注入MTPA控制策略,弥补了一般虚拟直流信号注入法的误差,设定的自适应律在保证最优工作点跟踪准确性的同时,简化了∂Te/∂β的计算。通过对虚拟直流信号注入法在极值处的稳态分析可以得出,虚拟直流信号注入法可以避免真实信号注入对电磁转矩产生的扰动,通过对获取直轴电流参考值的改进,有效减少系统在极值处的转矩变化,验证了控制策略在最大转矩电流比极值处的局部稳定性。idref获取中积分器的设置决定了控制系统的稳定性与动态性能。虚拟信号的幅值大小决定了∂Te/∂β的精度并不会影响系统的动态性能。仿真结果也验证了所提控制方法的可行性。
