射流通道内方柱发热器件的几何设计*
2022-10-12谢志辉关潇男孟凡凯戈延林
饶 凯,谢志辉,关潇男,孟凡凯,戈延林
(1.海军工程大学 动力工程学院,武汉 430033;2.武汉工程大学 热科学与动力工程研究所,武汉 430205;3.武汉工程大学 机电工程学院,武汉 430205)
引 言
随着电子技术的发展,电子器件的性能不断提升,其散热需求日益增强,流体冷却方式成为突破该类散热瓶颈的重要技术手段之一[1-4].研究发现,发热器件的间距和长度变化对器件散热性能有重要影响[5-6].在电子系统中,常常包含一个或几个高散热组件,一种解决其散热问题的可行方法是采用T 形通道射流冷却,即将冷却流体由垂直通道射入,通道射流入口被设置在高散热部件上方,横流则为其他需要较低冷却能力的器件提供均匀的冷却环境.Rundstroem 等[7]研究了冲击射流的Reynolds 数、横流的Reynolds 数以及顶板与底板之间的距离对流场的影响,其中停滞点、分离、回流和曲率效应等与流动相关的因素会影响传热速率和压降.Meghdir 等[8]以有限体积法为基础,研究了电子元器件在气流通道中受到冲击射流时,电子元器件的几何形状对冷却效率的影响.此类散热解决方案不会直接增加电子器件的重量、体积和成本,但能提升装备的可靠性.
熵产反映了传热过程的不可逆耗散,Bejan[9-10]推导了有限压差流体流动和有限温差传热的熵产率公式,并应用在传热过程优化中,由此提出了熵产生最小化原理.Rehman 等[11]对具有新型侧壁肋片结构的微通道散热器内的流体传热特性进行了数值研究,发现水翼型侧壁肋条可使系统熵产率最小.Pati 等[12]对高Prandtl 数流体层流强迫对流作用下圆管壁面热流的非均匀分布进行了数值研究,与均匀加热相比,该加热策略产生的熵产率和峰值温度更小.Kingston 等[13]利用基于速率分布的Taylor 和Krishna 模型,研究了低压填料蒸馏塔中的空气分离规律,通过数值优化确定了使系统熵产率最小的换热温度分布.
Bejan 研究了各种自然树状网络结构生成的普遍物理机制,发现了构形定律,提出了构形理论,为热设计优化开辟了新的途径[14-19].构形定律可简要表述为:事物结构源自于性能达到最优[16].Mustafa 等[20]在固定压降条件下,自由改变大管间距和小管轴长,以系统最大换热密度为优化目标,以大管间距为约束条件,对二维通道横流中的双尺度菱形管进行了构形优化.Abbas 等[21]对纵向翅片管的三种布置方式:前翅片、后翅片和等宽度前、后翅片进行构形设计,实现了从翅片管到通道横流的热流密度最大化.Ahmed 等[22]以管的垂直轴长和管间距为优化变量,以系统最大换热密度为优化目标,以管的高度和管的水平轴长为约束条件,对二维通道中的单排菱形管进行了构形优化.Yu 等[23]设计了一种新型的构形分支回热器,研究了不同丝网倾斜角对回热器热力特性的影响.Gong 等[24]以变截面圆柱体热源为研究对象,进行了以无量纲热点温度最小为目标的构形优化.范旭东等[25]以变物性条件下圆柱体热源为研究对象,进行了以火 积当量热阻和最大热阻最小化为目标的构形优化.王刚等[26]建立了圆柱体热源的三维湍流散热模型,研究了导热系数、热源强度和流体流速对器件最高温度、火 积当量热阻和平均Nusselt 数的影响.Teixeira 等[27]在强迫对流条件下,以热源间纵向和横向距离与自身尺寸的比值为优化变量,以热源的横截面积和热源排列的占用面积为约束条件,以系统阻力系数最小为优化目标,对二维通道中按照三角形排列的方形钝体热源进行了构形优化.Aghenese 等[28]以最大化Nusselt 数和最小化气缸与周围流动之间的阻力系数为优化目标,以圆柱横向间距与圆柱直径之比为优化变量,以四个圆柱的总体积为约束条件,对四个交错排列的圆柱热源模型进行了构形优化.Razera 等[29]以椭圆柱之间的垂直距离和椭圆柱的长短轴比为优化变量,通过改变流体的压力差,以椭圆管的横截面面积为约束条件,以换热密度最大化为优化目标,对二维通道中的椭圆柱热源进行了构形优化.Wang 等[30]以无量纲熵产率最小为优化目标,以导热系数分布与热源强度分布为优化变量,以热源总发热功率和各热源导热系数之和为约束条件,分别得到了椭圆柱离散热源的最优热源强度分布和最优导热系数分布.
在给定约束条件下,通过研究事物外形和结构的演化与性能变化的规律以获得最优设计结果,是工程构形设计的核心思想[15-19].前述研究的热源均采用单入单出横向对流冷却的方式,本文采用单入双出射流冷却的方式,结合熵产生最小化原理和构形理论,以热源总纵截面面积和热源高度一定作为约束条件,以系统最高温度和熵产率最小为优化目标,以离散热源之间的长度比为优化变量,对射流通道内的方柱离散热源进行几何设计,研究射流速度、热源大小和位置分布对系统最高温度和熵产率的影响,可为实际发热器件的热设计提供理论指导.
1 数理模型和求解方法
1.1 几何模型
图1给出了二维T 形通道内方柱热源的几何模型,图2为整体网格图.其中热源处于一水平的矩形通道中,水平通道高为H,导热基座长度和厚度分别为L=4H和Hb=0.03H.通道上方有一矩形射流通道,其口径与水平通道长度L的比值为=0.1,射流速度为Uj.在基座中轴线上布置3个离散热源(如图1所示,编号为1,2,3),其中热源长度为di=0.1L,高度为h=0.2H,热源中点之间的距离从左至右依次为L1到L4,且

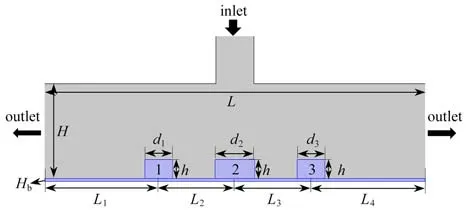
图1 热源几何模型图Fig.1 The geometric model for heat sources

图2 整体网格图Fig.2 The overall grid pattern
设三个方柱热源的高度相等,且d1=d3,L2=L3,有热源长度比

热源之间的间距与通道总长度的比值为

构形设计的几何约束为离散热源的纵截面面积A和热源高度h一定,即

将式(2)代入式(4),可得到

离散热源为均匀产热,热源的总产热率给定,3个离散热源的热源强度均相等.
在式(1)~(5)的几何约束条件下,以热源之间的长度比β为优化变量,以系统最高温度和熵产率最小为优化目标,对二维T 形通道内方柱热源进行构形优化.
1.2 传热模型
导热基底材料为硅(定压比热容cp=700 J·kg-1·K-1,密度ρ=2 329 kg·m-3,导热系数λb=130 W·m-1·K-1),热源材料为铜(cp=385 J·kg-1·K-1,ρ=8 960 kg·m-3,λs=400 W·m-1·K-1).T 形通道中冷却介质为空气,通道内流体的流动为可压缩稳态湍流流动(Re=2 889 ~8 668),通道外壁面为绝热边界条件,通道、热源与空气的接触面为无滑移边界条件,射流入口速度Uj垂直于入口端面,该处环境的空气温度设为293.15 K,通道两出口端面为压力边界条件.
空气流动的连续性方程、动量方程、能量方程、湍动能方程、湍流耗散率方程和湍流黏度方程分别为[21]

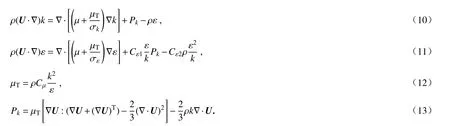
式(7) ~(13)中,I为单位矩阵,F为体积力,µ为分子黏性系数,µT为湍流黏性系数,k和ε 分别为湍动能和湍流耗散率,Q为包含黏性耗散和压力功在内的热源项,Pk为湍动能的生成项.Cε1,Cε2,Cµ,σk,σε均为经验常数,取值分别为[25]:Cε1=1.44,Cε2=1.92,Cµ=0.09,σk=1,σε=1.3.
常物性固体基底稳态导热的能量方程为

常物性热源稳态导热的能量方程为

图1所示散热系统的熵产率为
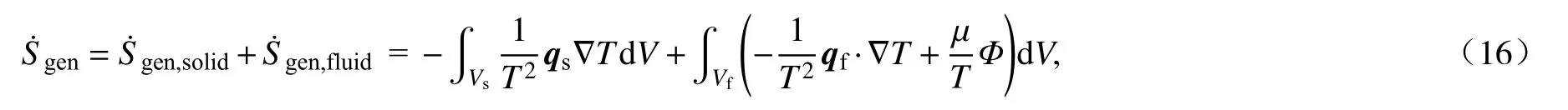
式中,等号右侧括号中第一部分为固体熵产率,第二部分为流体部分产生的熵产率.Ф为单位体积黏性耗散函数,q为热流密度矢量,单位W·m-2;µ为分子黏性系数,单位Pa·s.
综上所述,图1所示模型的构形设计问题可概括如下:
① 优化对象,射流通道内的方柱热源;
② 优化目标,系统最高温度和熵产率;
③ 优化变量,热源间的长度比;
④ 约束条件,热源纵截面面积和热源高度一定;
⑤ 影响因素,热源间距占通道长度的比值和射流速度.
1.3 数值求解方法
利用COMSOL Multiphysics 有限元数值计算软件求解散热模型的控制方程和边界条件.采用标准k-ε 湍流模型,对固体和流体区域分别进行边界层网格和自由三角形网格剖分,对网格独立性进行了测试.在离散热源的长度和高度都相等,热源间距占通道总长度比值γ=0.2的情况下,利用物理场控制网格,单元大小按细化、较细化和超细化标准设置,对数值计算结果进行验证,3 套网格的数量、对应的单元体内最高温度及相对误差如表1所示.考虑计算精度和效率,选择单元数为69 132的较细化网格划分策略计算网格.连续性、动量和能量方程的收敛标准均为1 × 10-6.

表1 网格独立性检验Table 1 The grid independence test
为了进一步评估本文计算模型的准确性,建立文献[22]的热源模型,其中为热源圆柱体的无量纲高度,b为肋片和热源中心距与肋片半径的比值,以无量纲最大温差为评价指标进行对比,结果如表2所示.对于相同的和b,的最大相对误差为0.85%,说明本文算法是可靠的.

表2 模型有效性验证Table 2 Validation of the model
2 结果与讨论
2.1 最高温度最小化构形设计
图3~5 给出了速度大小Uj分别为1 m/s,2 m/s 和3 m/s,热源间距占比γ=0.2,0.3 和0.4 时,热源长度比β与最高温度Tmax的关系.
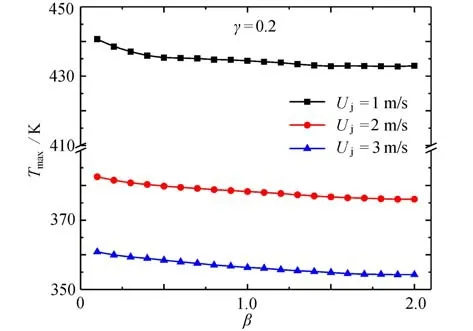
图3 γ=0.2 时,Uj 对Tmax 与β 关系的影响Fig.3 Effects of Uj on the relationship of Tmax vs.β for γ=0.2
如图3所示,当γ=0.2 时,Tmax均随β的增大而减小,最后趋向于平稳.这表明热源2(即射流入口下方的热源)长度越小,两侧热源长度越大,则热源的最高温度越小.但随着β持续增大,Tmax减小的趋势减缓并趋于稳定,此时提高β已难以改善系统散热性能.当β给定时,随着Uj的增大Tmax减小,即射流速度越大,系统散热效果越明显.
如图4所示,当γ=0.3 时,Tmax均随β的增大先减小后增大,即存在最优的βopt,使得Tmax取得最小值Tmax,min.当β<βopt时,Tmax的递减斜率较大,即β的大小对Tmax的影响较大;当β>βopt时,Tmax的递增斜率较小,即β大小对Tmax的影响较小.这主要是由于热源2 距离射流入口较近,当其长度较大时,受射流垂直冲击的散热面较大,散热效果较好,而两侧热源距离射流入口较远,因此其长度大小的变化对散热效果的影响较弱.
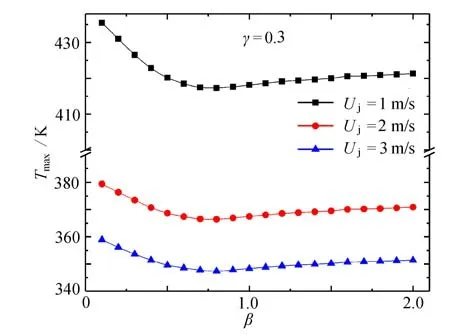
图4 γ=0.3 时,Uj 对Tmax 与β 关系的影响Fig.4 Effects of Uj on the relationship of Tmax vs.β for γ=0.3
由图5可知,当γ=0.4 时,Tmax均随β的增大先减小后增大,且均存在最优的βopt,使得Tmax取得最小值Tmax,min.这表明实际应用中,随着热源间距的增大,设计人员可考虑将靠近射流入口的发热器件的长度增大,两侧发热器件长度减小,增大受射流冲击面,降低系统温度.
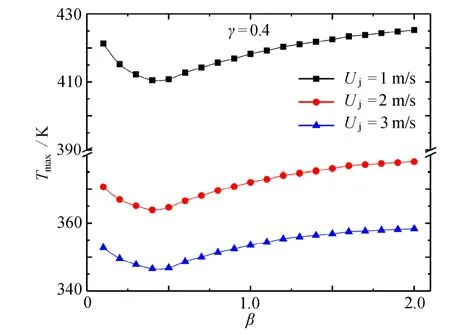
图5 γ=0.4 时,Uj 对Tmax 与β 关系的影响Fig.5 Effects of Uj on the relationship of Tmax vs.β for γ=0.4
综合对比图3~5 可知,当Uj和β给定时,随着γ的增大,Tmax减小.这主要是因为热源间距增大时,射流流体能够更加充分地冲击导热基座,使得导热基座的散热效果增强,间接地强化了热能从高温热源向低温导热基座转移的过程,从而提升了热源的散热效果.并且,随着γ的增大,βopt减小.这表明,随着热源之间的间距增大,导热基座受射流冲击的表面积增大,其散热效果增强.同时,热源2 长度的增大也增加了与导热基座的接触面积和受射流冲击的表面积,更有利于散热.而两侧热源由于距离射流入口较远,所以其长度的变化对热源散热效果的影响较小.
表3给出了不同Uj和γ 与最优长度比βopt和Tmax,min之间的关系.
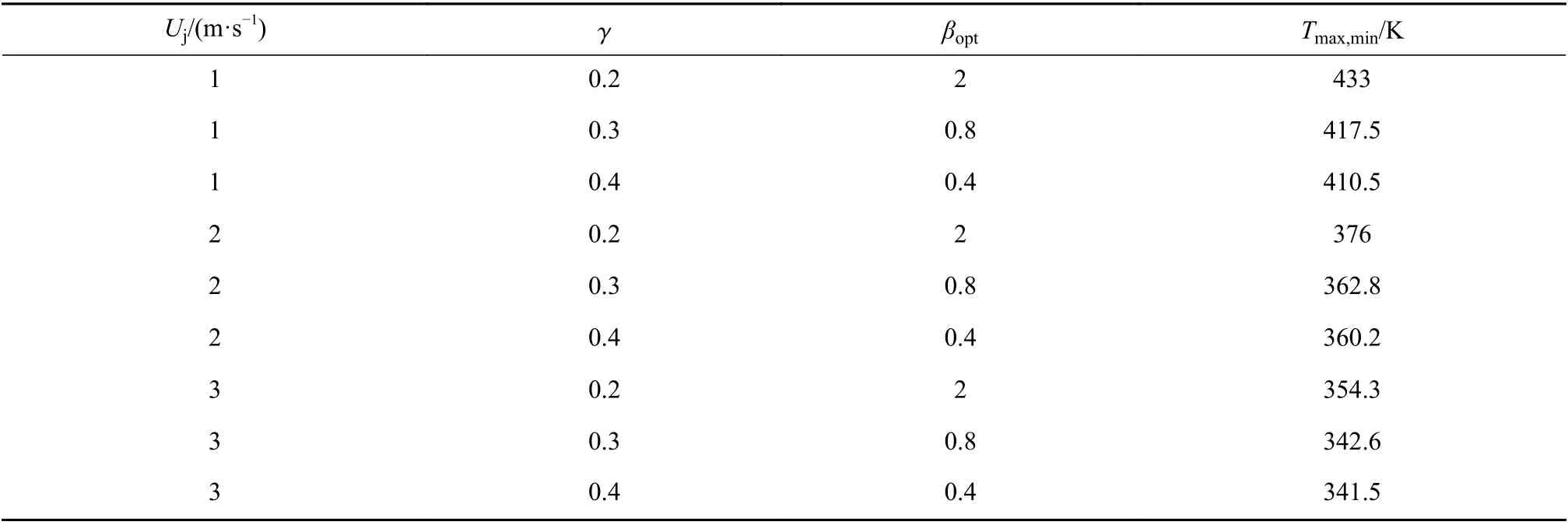
表3 不同Uj 时,Tmax,min 及对应的几何参数Table 3 Tmax,min and its corresponding geometric parameters for different Uj values
图6~8给出了3 种间距下,速度大小Uj为3 m/s 时,取最优长度比时的温度等值线图.从图中可以看出,随着γ的增大,等值线图的高温区域逐渐靠近通道底部和两侧出口处,射流入口附近始终是温度最低区域.γ=0.2 时,高温区域的面积比γ=0.3 和0.4 时的高温区域的面积要大.而γ=0.3 时,导热基座上的高温点比γ=0.4 时的高温点分布更加均匀,且均位于各离散热源的两侧.
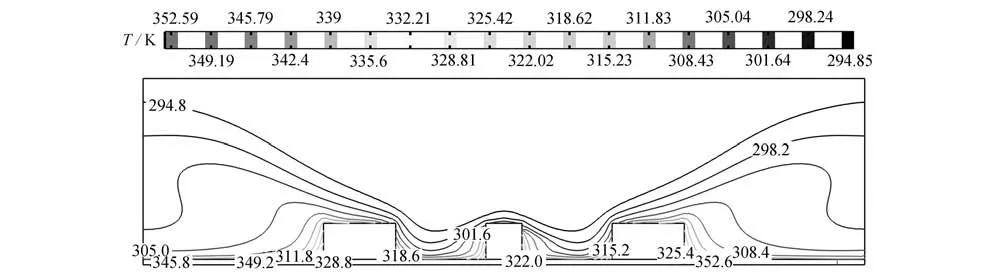
图6 γ=0.2,β=2,Uj=3 m/s 时,温度的等值线图Fig.6 The temperature contour map for γ=0.2,β=2,Uj=3 m/s
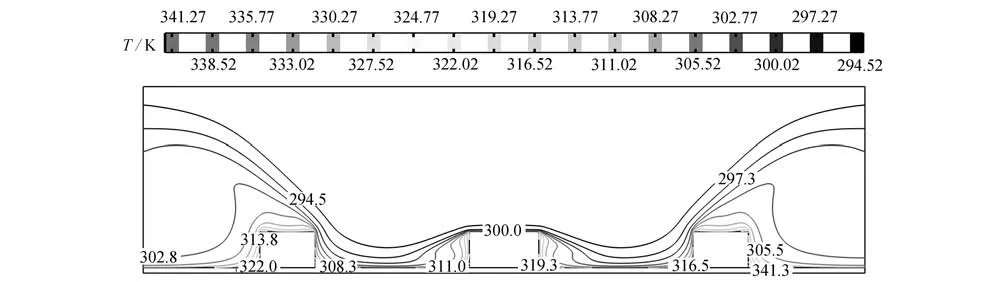
图7 γ=0.3,β=0.8,Uj=3 m/s 时,温度的等值线图Fig.7 The temperature contour map for γ=0.3,β=0.8,Uj=3 m/s
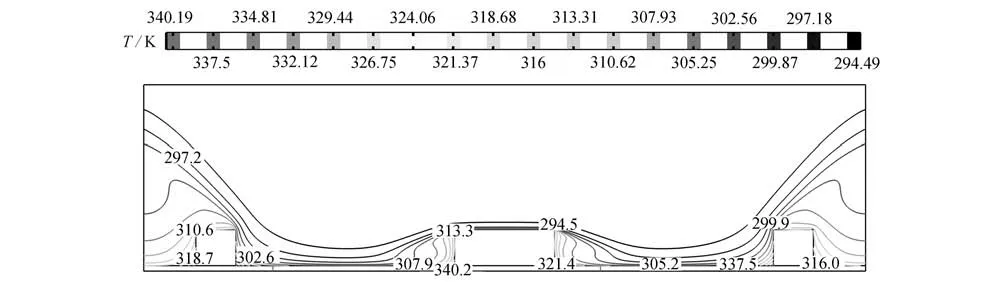
图8 γ=0.4,β=0.4,Uj=3 m/s 时,温度的等值线图Fig.8 The temperature contour map for γ=0.4,β=0.4,Uj=3 m/s
2.2 熵产率最小化构形设计
图9~11 给出了速度大小Uj分别为1 m/s,2 m/s 和3 m/s,热源间距占比γ=0.2,0.3 和0.4 时,热源长度比β与系统熵产率的关系.
注为了解释图中的颜色,读者可以参考本文的电子网页版本,后同.
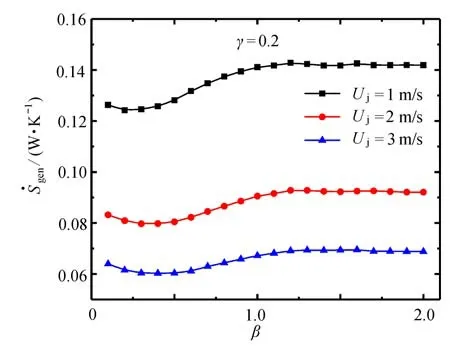
图9 γ=0.2 时,Uj 对 与β 关系的影响Fig.9 Effects of Uj on the relationship of vs.β for γ=0.2
由图10可知,当γ=0.3 时,随着β的增大先减小后增大,存在最优长度比βopt使得达到最小值.当β<βopt时,的下降斜率较大.当β>βopt时,的上升斜率较小.这说明,当热源2 长度大于两侧热源长度时,β对的影响较大,而当热源2 长度小于两侧热源长度时,β的增大对的影响较小.这主要是因为β的减小增加了两边热源与射流入口的距离,使得射流冲击两边热源的流动减弱,使一部分流体动能不可逆地耗散为热,增加了系统熵产率.
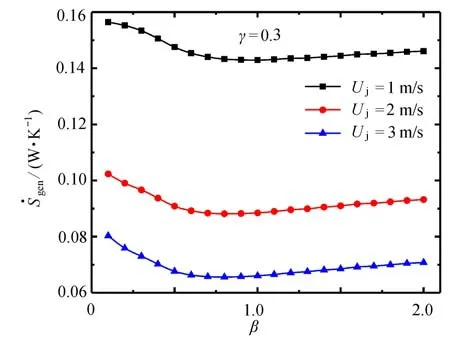
图10 γ=0.3 时,Uj 对 与β 关系的影响Fig.10 Effects of Uj on the relationship of vs.β for γ=0.3
由图11可知,当γ=0.4 时,随着β的增大先减小后增大,存在最优长度比βopt使得达到最小值.不同的是,当β大于或小于βopt时,单调增减的斜率相近.这表明,当热源间的间距增大后,热源间流场的流动更充分,使得热源之间的长度比对流体流动的影响趋于相同.
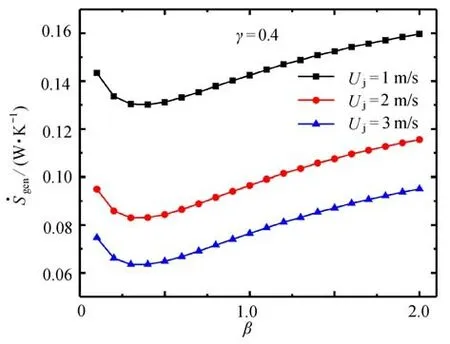
图11 γ=0.4 时,Uj 对 与β 关系的影响Fig.11 EffectsofUjonthe relationship of vs.β for γ=0.4
综合图9~11 可知,当Uj和β给定时,随着γ的增大,βopt先增大后减小.这主要是因为当热源间距增大时,两侧热源距离射流入口较远,受射流冷却流体的影响减小,所以其长度对对流传热效果的影响较小,而热源2 长度增大后其影响增大,导致βopt减小.当热源间距减小时,导热基座受射流冲击不充分,且βopt较小时,热源2 上表面的增大阻碍了流体向两边出口的流动,流体在热源上表面形成反射气流,增强了涡旋,使流体旋转动能转变为热能.
表4给出了不同Uj和γ 与最优长度比βopt和之间的关系.
表4 不同Uj 时,及对应的几何参数Table 4 and its corresponding geometric parameters for different Uj values
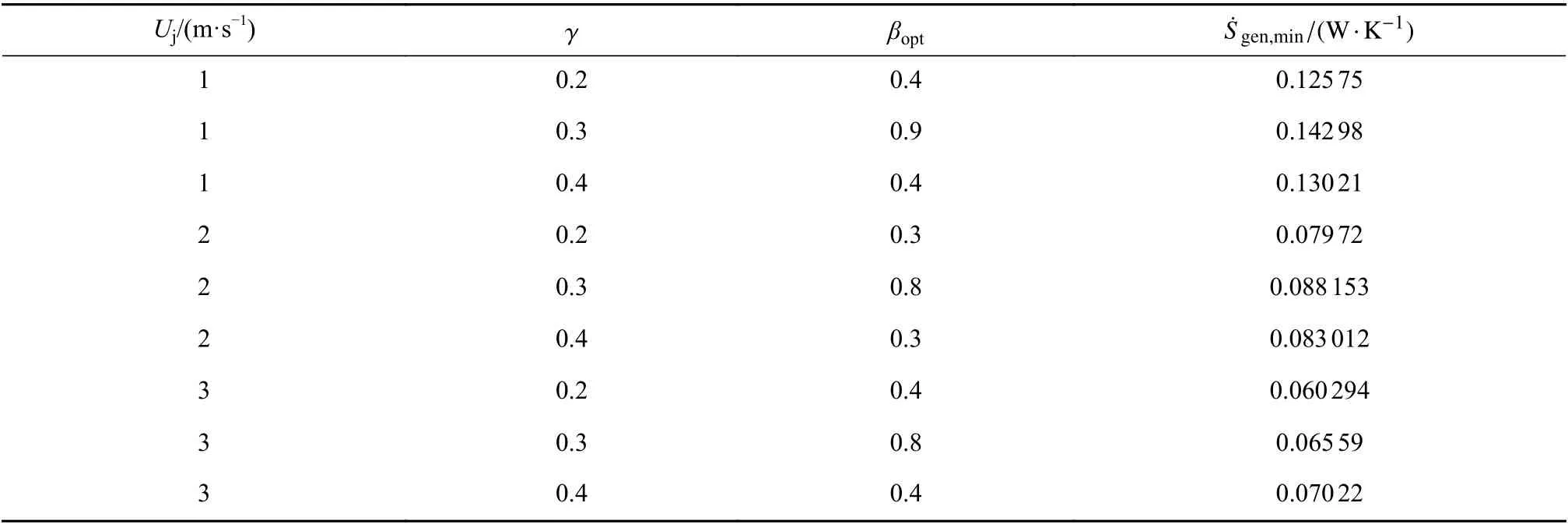
表4 不同Uj 时,及对应的几何参数Table 4 and its corresponding geometric parameters for different Uj values
Uj/(m·s-1) γ βopt ˙Sgen,min/(W·K-1)1 0.2 0.4 0.125 75 1 0.3 0.9 0.142 98 1 0.4 0.4 0.130 21 2 0.2 0.3 0.079 72 2 0.3 0.8 0.088 153 2 0.4 0.3 0.083 012 3 0.2 0.4 0.060 294 3 0.3 0.8 0.065 59 3 0.4 0.4 0.070 22
图12~14给出了三种间距下,速度大小Uj分别为1 m/s,2 m/s 和3 m/s 时,最优长度比的通道纵截面的速度分布图.随着γ的增大,射流与导热基座的接触面积不断增大,这使得通道内流体流动克服沿程摩擦力所产生的能量损失不断增大.同时,热源的存在,使得流体的流动在热源处、热源上方和热源之间存在明显的局部绕流、流动阻滞和涡旋,其中流动阻滞增大了流动的耗散,涡旋强化了流体与热源之间的对流传热.

图12 γ=0.2,β=2,Uj=3 m/s 时,通道纵截面的速度分布图Fig.12 The velocity profile of the channel longitudinal section for γ=0.2,β=2,Uj=3 m/s

图13 γ=0.3,β=0.8,Uj=3 m/s 时,通道纵截面的速度分布云图Fig.13 The velocity profile of the channel longitudinal section for γ=0.3,β=0.8,Uj=3 m/s

图14 γ=0.4,β=0.4,Uj=3 m/s 时,通道纵截面的速度分布云图Fig.14 The velocity profile of the channel longitudinal section for γ=0.4,β=0.4,Uj=3 m/s
3 结 论
本文建立了二维T 形通道内的方柱离散热源散热模型,研究了在离散热源纵剖面面积和热源高度一定的约束条件下,热源之间的长度比、间距和入口射流速度对系统最高温度和系统熵产率的影响.主要结论如下:
1) 当离散热源纵剖面面积和热源高度一定时,分别存在不同的最优热源长度比使得系统最高温度最小和系统熵产率最小.
2) 当热源之间长度比和入口速度一定时,热源间距越大,系统最高温度最小值越小,而系统熵产率最小值越大.
3) 当热源之间的长度比和间距一定时,入口射流速度越大,系统最高温度和系统熵产率越小.
4) 当热源间距较小时,增大热源之间的长度比有利于降低系统的最高温度;当热源间距较大时,减小热源之间的长度比有利于降低系统的最高温度.并且,在不同间距条件下,最高温度最小值所对应的最优热源长度比也不同.
