一种两维数字阵列干扰测向的快速方法

崔向阳 刘 颖 付学斌 田 欢 陈 亮 王爱荣

(1.西安电子工程研究所 西安 710100；2.西安现代控制技术研究所 西安 710065)

0 引言

随着电子战技术的发展，雷达工作的电磁环境日益复杂，在检测目标的同时，需要高效的对抗空间干扰。对有源干扰的感知和测量是雷达抗干扰的前提，干扰源定向技术通过对空间信号进行采样处理，估计出辐射源的方位、俯仰信息，为抗干扰提供先验信息。

对干扰源定向的常用方法主要有：

1)比幅测向法，即通过对侦查空间进行波束的全扫描，当波束扫描到干扰源时，利用比幅方法进行测角，这种方法对波束扫描及占用的系统资源都有要求；

2)相位干涉仪测向，利用鉴相方法来估计干扰源方向，这种方法需要基线长度有一定要求；

3)空间谱估计及超分辨的方法，方法以MUISC，ESPRIT等算法为代表，具有多角度分辨和高精度的特点，但是实现方式较为复杂。

与此同时，大规模数字处理器件的快速发展，更大规模的数字阵列雷达，越来越多地进入到了工程研制阶段，为干扰测向提供了更多的可能性。干扰入射方向的估计，属于波达方向估计的范畴。传统的雷达，由于系统的自由度不够，能够采用的波达方向估计技术并不多。在数字阵列中对于波达方向的估计，如MUISC、ESPRIT等算法，这些算法虽然测角精度高，但是考虑到雷达工作的波束驻留时间很短，工程应用中受限于运算时间的要求难以实现，而对于两维数字阵列，其复杂度进一步提高。

1 FFT进行空间DOA估计

对于一均匀线阵，其阵元个数为，其阵元间距为，为载波信号的波长。对于远场个窄带入射信号的时间平稳信号，其如入射角为，其第个阵元的输出为

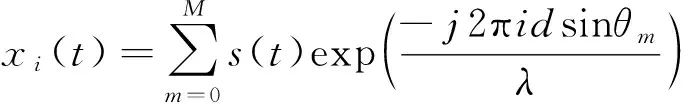
(1)

其中，=1,2,…,-1；()为入射信号。

对比FFT的表达式为

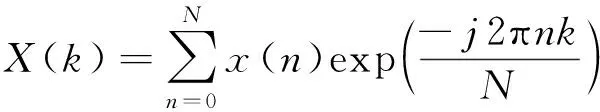
(2)

其中，FFT后第个谱峰对应的空间采样点为；_FFT为FFT的点数，通过对应与FFT的关系，获得空间采样频率，第谱峰对应的入射角度为

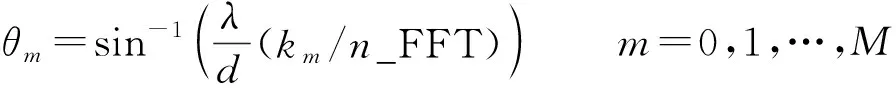
(3)

对于FFT估计的角度分辨率，其瑞利限(均匀线阵)由3 dB波束宽度决定为

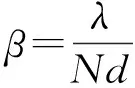
(4)

2 两维空间方向估计

两维数字阵列其，分别为行、列阵元间距，行列阵元数分别为，，其全阵面接收的第个采样快拍的数据矩阵为

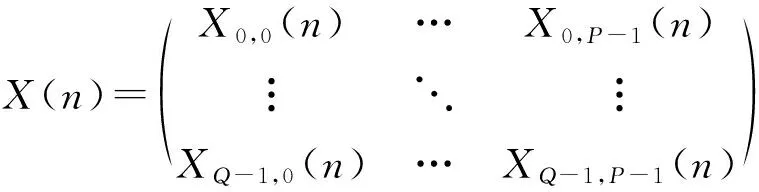
(5)

本文中所提到的干扰测向方法，首先需要进行接收数据的选取。需要对两维子阵平面中，选取一个“十字架”，见图1所示，即中间的一行及一列，进行干扰测向。对于单个阵元，阵元的辐射的特性可近似认为为全向天线。这样选取某一列的所有行，见式(6)所示。

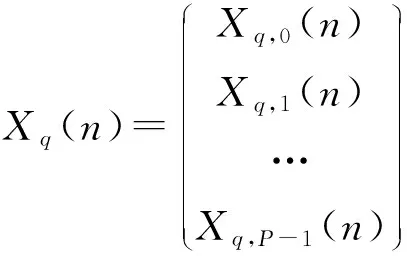
(6)

则在方位维可近似认为全向波束，俯仰维为一维线阵，可以进行俯仰维干扰角度测向。同样的，选取某一列的所有行，即

()=(0,()1,()…-1,())

(7)

则在俯仰维可近似认为全向波束，方位维为一维线阵，可以进行方位维干扰角度测向。

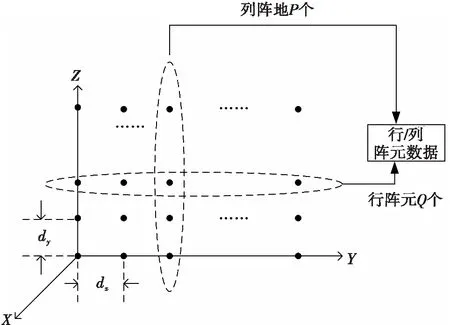
图1 阵面阵元选取平台示意图

其对应的方位角和俯仰角分别为式(8)和式(9)所述，此角度为阵面坐标系下的锥扫描角，n_FFT为FFT点数。

其中方位角为

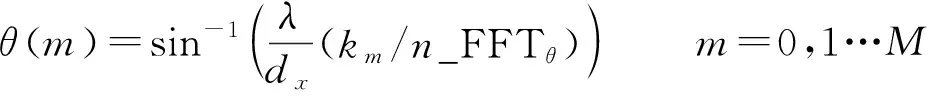
(8)

其中俯仰角为

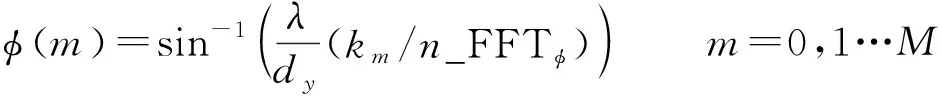
(9)

3 空间方向匹配

为了提高估计的可信度，干扰估计需要对多次快拍进行处理，假设共采样个快拍，(),=0,1,…,，为天线阵面“列”采样点；(),=0,1…,，为天线阵面“行”采样点。通常情况下，由于快拍采样过程极短，入射干扰角度几乎没有变化，那么多次快拍之间干扰入射角度应该一致，即个干扰的入射角度为式(10)所示。

=[(0)(1) …()]

(10)

此外则测得的FFT后的峰值位置也应一致。个快拍个干扰入射对应的谱峰位置的信号如式(11)所示。

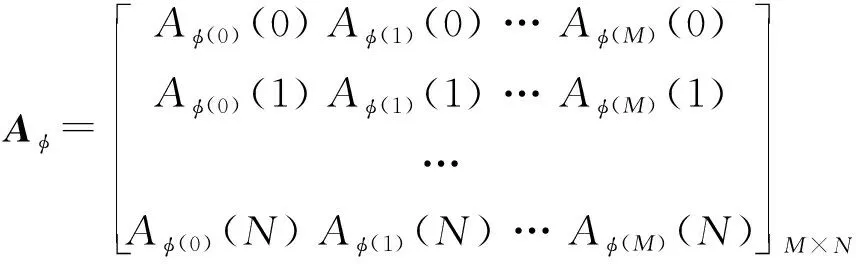
(11)

计算获得方位维个干扰方向的次采样快拍的记录值为式(12)所示。

=[(0)(1) …()]

(12)

对应的谱峰位置的信号为式(13)所示。

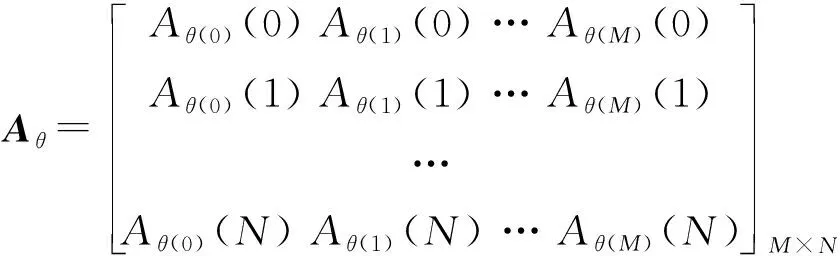
(13)

对俯仰维谱峰信号的矩阵×，及方位维谱峰信号的矩阵×，进行自相关运算。获得相关矩阵为式(14)所示。

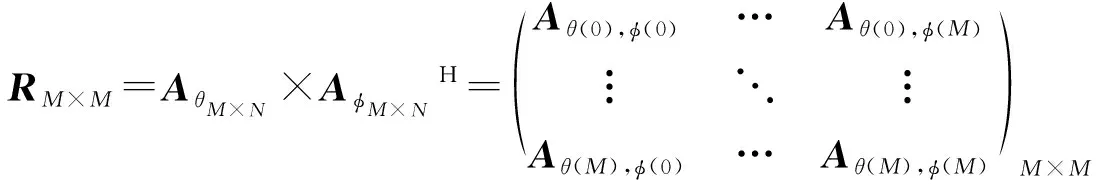
(14)

构造与相关矩阵对应的角度匹配矩阵，该矩阵并不计算具体数值，而是通过对矩阵1×，1×进行与×矩阵相同的矩阵运算过程，生成角度查找表。如式(15)所示。

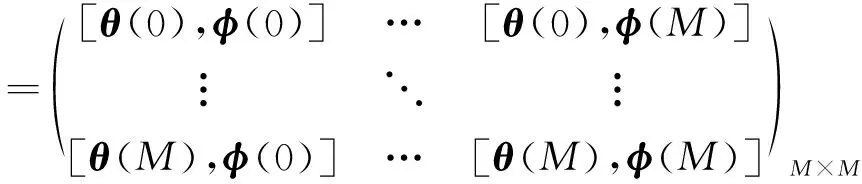
(15)

即(,)该点的方位角为()，俯仰角为()。

相关矩阵×幅度越大则表明相关性越大，即就是俯仰与方位角度配对程度越高。针对个干扰通过对相关矩阵×幅度排序后，获得个极值。通过个极值在×矩阵中的获得该极值数据的下标(,)，对比相关矩阵×与查找表×的对应关系，如图2所示，从矩阵×中，根据坐标(,)，并找到个配对的干扰角度(，)，完成干扰角度配对。

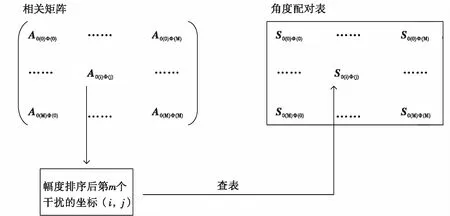
图2 角度配对示意图

4 实现流程

首先，设计雷达系统工作时序，增加静默侦查区，如图3所示。干扰测向是为干扰对消提供角度先验知识，所以在干扰测量时，如果有己方雷达的辐射信号进入干扰测量的通道，在对消时就会消去己方有用信号。所以需要在雷达发射周期中增加静默区，此时不辐射电磁信号，仅接收信号(干扰)。此时雷达静默工作，雷达阵面处于不发射仅接收状态。

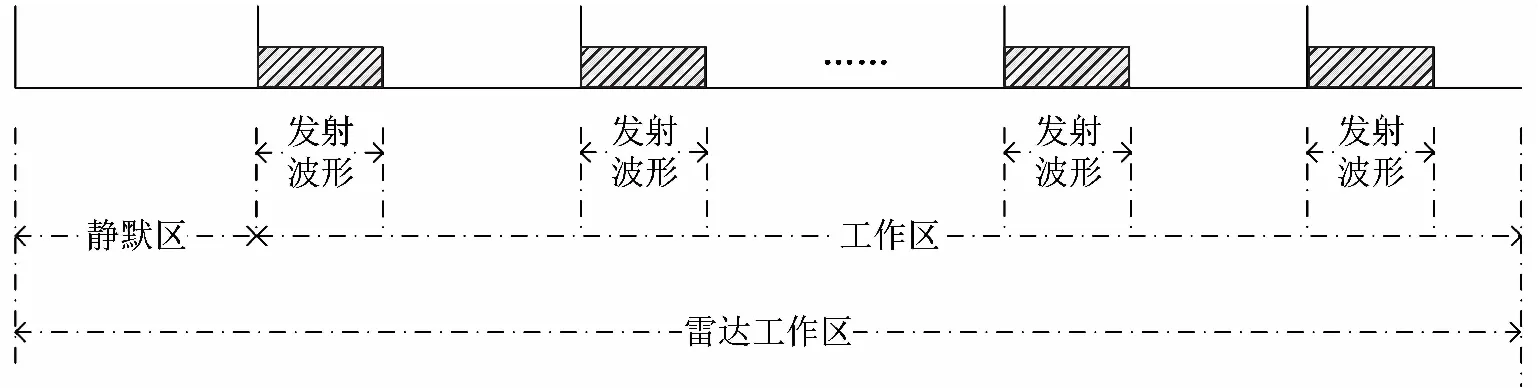
图3 雷达工作时序示意图

其次，在确定周围环境无干扰时(如天线暗室环境)，对行(或列)采样的快拍进行FFT，记录雷达正常工作时，统计雷达静默区的接收机噪声电平，并根据系统需求，当正常工作时静默区接收机噪声电平大于某一值时认为系统受到干扰，其中值可由上位机参数控制或设置经验值。正常工作时，如雷达静默区侦听到的信号高于门限一定数量时，判定为系统受到干扰。假设干扰的个数为个，通常设置为系统能够处理的最大干扰个数，这取决于系统能够对抗干扰的自由度和运算能力。

再次，按照第一，二章所述的方法。利用FFT方法进行干扰测向，充分利用数字阵列灵活的优势，单独处理“行”，“列”单次采样快拍进行FFT运算，可以获得方位、俯仰维指向干扰角度的FFT峰值点，记录其幅度是否大于门限值。

最后，采用第三章节所述方法，对测出的两维角度进行角度匹配，获得最终的处理结果。

其处理流程见图4所示，采用本文所述方法，在某研制雷达中取得了较好的测量结果。

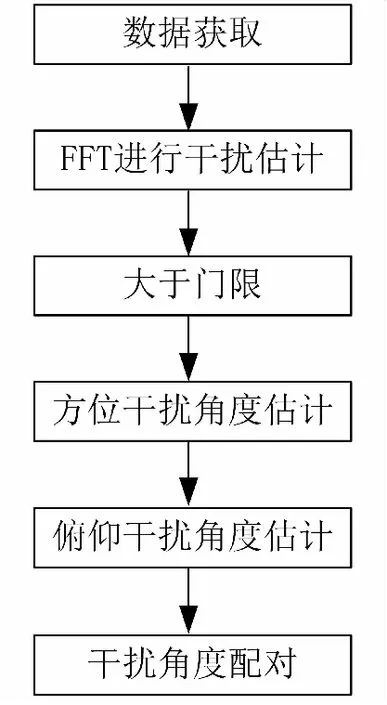
图4 处理流程示意图

这里通过仿真设置两个干扰源，其入射方向分别为：干扰1入射方位俯仰角为[-5,2]，干扰2入射方位俯仰角为[15,-15]。首先通过干扰估计可以获得方位俯仰的分别指向见图5所示，之后经过角度匹配的处理之后，获得其真实指向，分别为[-4.99，2.08]，[15.02，-15.06]。

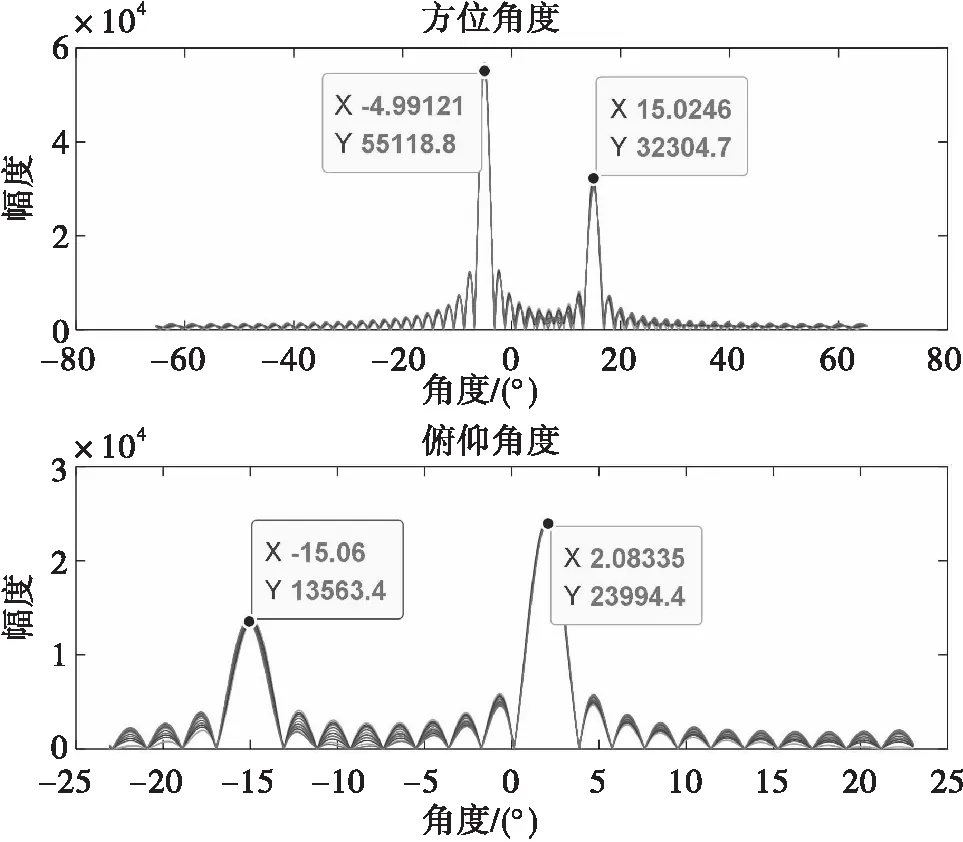
图5 多次采样快排进行FFT角度估计

实验中，设置两个干扰源，且分别使用点频连续波和噪声干扰两种形式的干扰。由于实现条件限制，干扰源位置无法灵活变动，这里通过转动天线伺服，测量获得与天线法线偏离的角度后，通过读取伺服转动角度值并加到天线法线偏移值上，来获得测量真值。这里俯仰测试0°和5°，方位测试-5°和5°，即天线法线与伺服码盘0°对齐时，两个干扰角度为[-5,0]，[5,5]。之后伺服方位每5°转动测试一次，具体测试结果见表1所示。从表1能够看到，对噪声的干扰角度估计误差大于对点频的估计。噪声类型干扰角度的估计误差大约在0.3°，对点频类型干扰角度的估计误差小于0.1°。

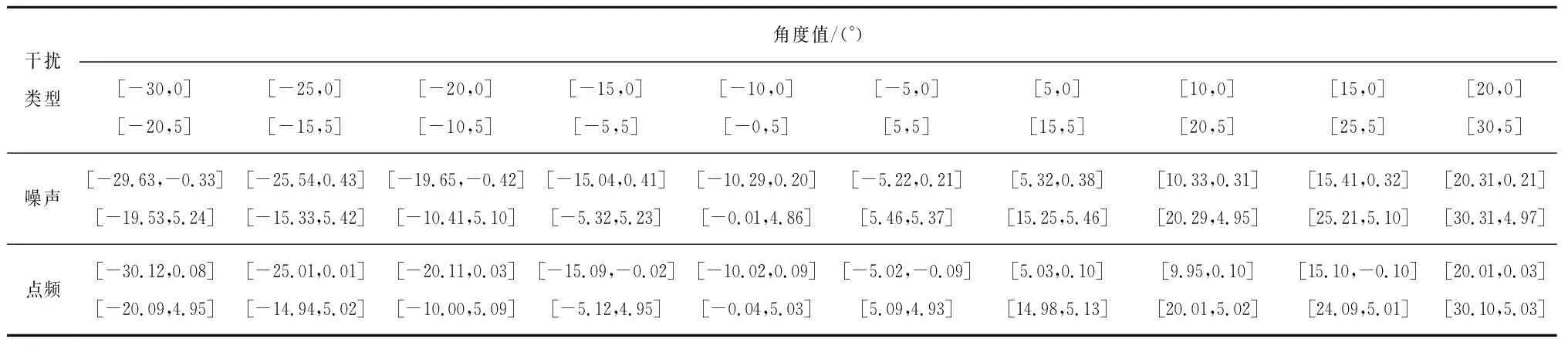
表1 实际测试结果

5 结束语

本文通过增加雷达发射静默周期，侦听环境干扰，同时通过对接收的数据进行分析，根据设置的门限阈值，判定是否有干扰进入，同时通过FFT的方法快速形成方向图，进行空域滤波搜索，获得方位、俯仰维度的干扰指向角度，之后通过对干扰入射方向的数据进行相关估计，完成两个维度的干扰角度配对处理，获得配对后的干扰入射角的方位、俯仰两维角度。具有相应速度快的特点，在对测向精度要求不高的场景，可以快速获得干扰的两维指向。