低空反无雷达的高精度测速方法及波形设计

杨雪亚 沈显照 王贤翔

(1.中国电子科技集团公司第三十八研究所 合肥 230088；2.孔径阵列与空间探测安徽重点实验室 合肥 230088)

0 引言

近年来，小型无人机在各行各业得到了广泛的应用，同时也给低空安全带来了巨大的挑战。小型无人机通常在低空或超低空飞行，飞行速度慢，且机身体积小，利用传统的检测手段很难将其从复杂的杂波背景中检测出来，这成为反无人机系统的技术难点。目前反无系统采用的探测手段包括声学探测、无线电扫描、光学探测及雷达探测，其中雷达探测凭借其全天候、全天时、探测距离远、测量精度高等特点，成为反无系统的首选。

国内外在低空反无雷达方面了做了大量的研究，文献[4]研究了低空小型无人机雷达的探测距离，给出了无人机RCS的计算模型和雷达方程。文献[5]给出了基于深度学习的特征提取的无人机检测识别方法。文献[6]研究了基于无人机旋翼微多普勒效应的目标检测和跟踪方法。文献[7]研究了长时间积累提高小型无人机检测信噪比的思路，并进行速度估计和运动补偿消除运动目标的距离徙动和多普勒扩散。文献[8]利用线性调频信号的距离多普勒耦合现象实现单脉冲测速。文献[9]提出了一种对目标回波主瓣面积梯形近似并插值估算多普勒频率最大值位置的方法。

本文针对杂波背景下低空反无雷达对小型无人机的探测问题，研究提高测速精度、改善杂波背景下无人机探测能力的方法。首先给出了采用基于多普勒频道幅度服从高斯分布的高精度测速方法，显著提高了无人机的速度测量精度。然后采用一种通过短、长脉冲交替发射增大短脉冲积累时间的波形设计方式提升速度分辨力。最后通过仿真和实测数据处理结果验证了本文方法的正确性。

1 信号模型

低空反无雷达通过发射线性调频脉冲及脉冲串MTD滤波的方式获取脉冲压缩增益和相参处理增益。线性调频信号形式为

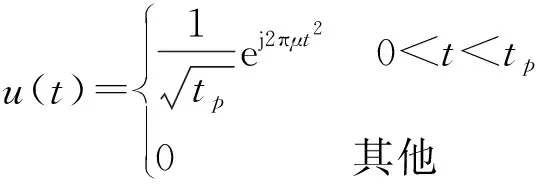
(1)

第个脉冲回波信号经脉冲压缩后可表示为

(2)

其中，为线性调频信号的时宽带宽积；为信号带宽；为回波延迟时间；为脉冲重复周期。

对脉冲压缩信号做阶MTD滤波处理，则第个滤波器的幅度响应为

(3)

滤波器的峰值位于=±,1±,2±处。相邻滤波器的频率间隔为

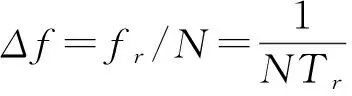
(4)

式(4)表示多普勒分辨力，为积累时间的倒数。则速度测量误差为式(5)所示。

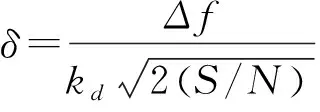
(5)

其中为测速环路误差斜率，一般可取12～14之间。

2 高精度测速方法

设目标的多普勒频率为，回波信号经过波束形成、脉冲压缩及MTD滤波之后，在第个MTD滤波器的幅度最大为，在前、后相邻滤波器的幅度分别为-1和+1，三组滤波器的中心频率分别为-1,,+1，如图1所示。

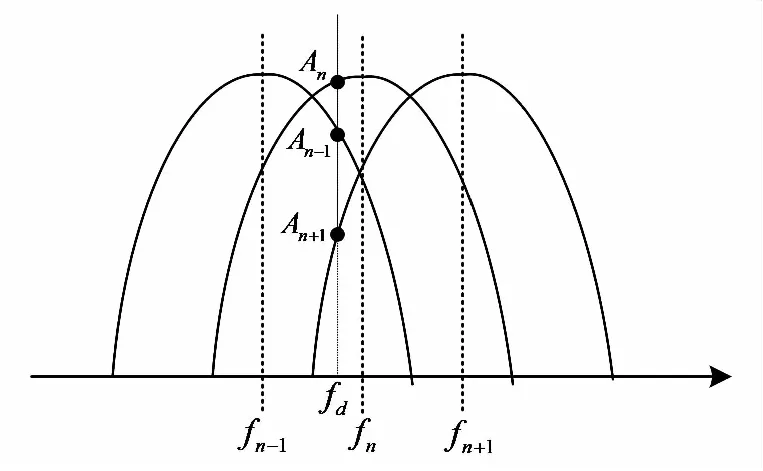
图1 高精度测速方法示意图

MTD滤波器的响应可认为服从高斯分布，且每组滤波器的响应曲线一致，则三组滤波器的幅度响应可表示为

=e-(-),=-1,,+1

(6)

其中为滤波器中心的幅度，为比例常数。

对和-1取对数并相减，可得

=--1=[(--1)-(-)]

(7)

同理，对和+1取对数并相减，可得

=-+1=[(-+1)-(-)]

(8)

由式(7)和式(8)可得

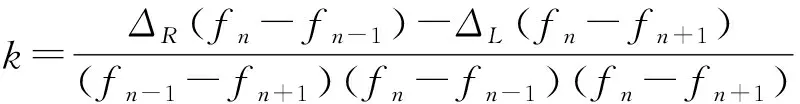
(9)

将式(9)代入式(7)，经过运算可得

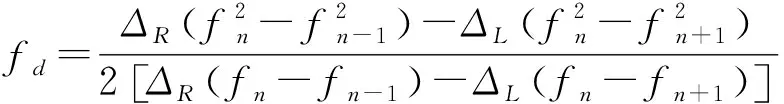
(10)

对于中心频率等间隔的MTD滤波器，--1=+1-，则式(10)可简化为

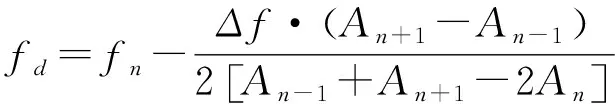
(11)

相比基于均匀分布的质心法，式(11)的计算方法更接近MTD滤波器的真实幅度响应曲线，因此能改善多普勒速度的测量精度。

3 长时间积累波形设计

低空反无雷达需要探测近区小型无人机和远区空中目标，因此采用近距离补盲和远距离正常两种波形。对于近距离补盲波形，其作用距离通常在10 km以内，而远距离正常波形的作用距离可达100 km。传统的波形设计方式是先后发射补盲和正常两组CPI，对两组CPI分别进行相参处理，补盲脉冲和正常脉冲的重复周期分别是1和2，脉冲数均为，如图2所示。

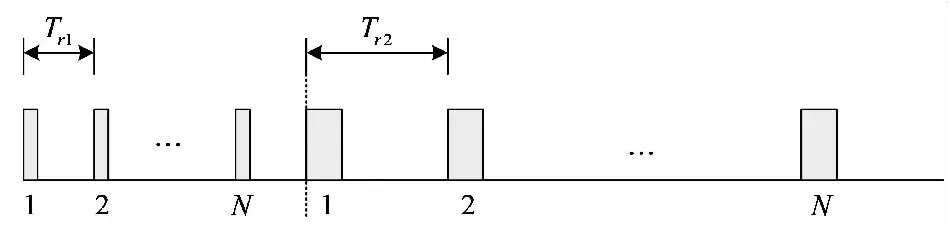
图2 传统的两组CPI发射波形

设1为0.1 ms、2为1 ms，积累脉冲数为64。补盲CPI的多普勒分辨力Δ=156.25 Hz，正常CPI的多普勒分辨力Δ=15.625 Hz。对于补盲CPI而言，其速度分辨力较低，显然无法利用速度信息将慢速运动目标从近区强杂波背景中分辨出来。

由式(4)和式(5)可见，通过增加积累时间，可提高速度分辨力和速度测量精度。因此，在总驻留时间不变的前提下，将上述发射波形进行优化，把每个补盲脉冲和正常脉冲合成为一个大脉冲，顺序发射个大脉冲，在后端处理时，将每个大脉冲内的补盲脉冲和正常脉冲分离出来，形成补盲、正常两组独立的CPI分别处理，如图3所示。

图3 改进的波形设计形式

对于近区补盲和远区正常波形，其积累时间均为70.4 ms，对应的多普勒分辨力14.2045 Hz，相比较传统的波形设计，补盲波形的速度分辨力提升了10倍以上，显著地改善了速度分辨力和测速精度。

4 仿真和实测数据处理

仿真径向速度为20 m/s的目标回波信号，采用重复周期为0.1 ms、64个脉冲的发射波形，比较不同测速方法的精度随积累信噪比的变化曲线，结果如图4所示。对于MTD滤波后直接选大的测速方法，受滤波器中心频率量化误差的影响，其测速精度跟目标多普勒速度与滤波器中心频率的相对位置有关(在0～0.5Δ间呈随机分布)。对于质心方法，由于均匀分布模型与真实分布模型偏差较大，导致测速误差大。而本文的高精度测速方法，根据三组滤波器的幅度和中心频率计算目标的速度，不受目标多普勒速度与滤波器中心滤波的相对位置关系的影响，更接近真实的分布模型，获得了更为准确的测速结果。

图4 测速误差随信噪比变化曲线

基于以上仿真条件，比较传统波形即补盲CPI、正常CPI先后发射，和补盲、正常脉冲交替发射的改进波形的测速精度，其中补盲脉冲和正常脉冲的重复周期分别为0.1 ms和1 ms。图5给出了补盲波形的测速误差对比结果，可见，改进波形的测速精度比传统波形提升了一个数量级。这是因为改进的波形将远距离正常脉冲的驻留时间包含在其积累时间内，显著提高了补盲波形的速度分辨力和测速精度。

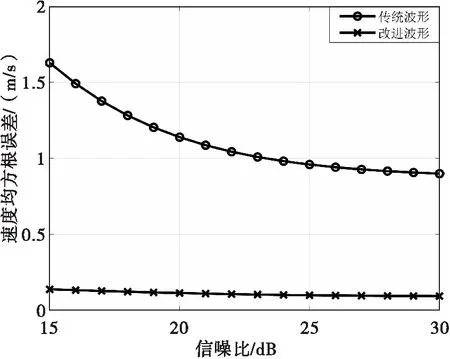
图5 传统波形和改进波形的测速精度对比

S波段低空反无雷达测试对大疆精灵四旋翼无人机的实际探测和测量性能，雷达使用补盲波形和正常波形交替发射的改进波形，在回波处理时将其分离成短、长两组CPI分别处理。无人机从雷达处起飞，以高度200 m、速度13 m/s匀速飞行至5 km处折返。雷达在距离600 m左右发现目标并按照1 Hz的数据率对无人机进行跟踪。图6是无人机飞行过程中雷达点迹的测量速度和无人机GPS记录的真实速度的比较，飞行前半段无人机背站飞行，后半段向站飞行，速度由-13 m/s变为13 m/s，雷达测量速度和无人机真实速度吻合较好。图7是雷达测速误差，可见最大速度误差不超过0.3 m/s，飞行全程均方根误差为0.075 m/s，实现了对小型无人机的高精度测速。

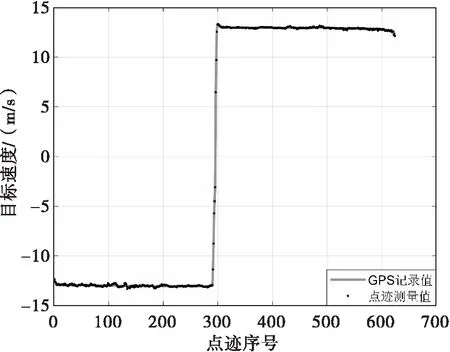
图6 无人机飞行速度真实值和测量值

图7 雷达对无人机的测速误差

5 结束语

“低、慢、小”目标的探测，尤其是强杂波区中小型无人机的探测一直是低空反无雷达的技术难点。为了更多地利用目标的速度信息对慢速运动目标和杂波进行分辨，本文给出了一种基于滤波器幅度响应服从高斯分布的高精度测速方法，与频道选大法和质心法相比，改善了速度测量精度。此外，采用一种改进的波形设计方式，充分利用整个驻留时间提升速度分辨力，在驻留时间不变的情况下，补盲脉冲的速度分辨力可提升一个数量级。仿真及实测数据分析结果表明了本文方法的有效性。