基于改进LMS算法的自适应旁瓣对消研究

刘喜洋 余建宇 陈 威 杨 伟

(1.西安电子工程研究所 西安 710100；2.中国人民解放军77618部队 拉萨 850000)

0 引言

在高科技战争的背景下，雷达所面临的电磁信号环境越来越复杂。雷达需要在复杂的电磁环境中对抗各种干扰。其中，敌方发射机产生的有源干扰是最难对抗的。雷达系统由天线非常窄的主波束引导，但每个天线波束都有旁瓣。其次，如果雷达处于强干扰环境中，来自旁瓣的干扰往往会压倒主瓣中的目标信号，这会对雷达系统的性能产生重大影响。超低旁瓣天线可以消除这种影响，但是研制开发的成本非常高。旁瓣对消技术使用附加的辅助天线处理器，通过信号处理消除来自主接收通道的旁瓣干扰，确保雷达系统正常运行。在自适应快速发展的背景下，加之数字处理和VLSL技术的应用和发展，自适应旁瓣对消系统已成为现代雷达等信息系统消除旁瓣干扰的重要工具。

LMS算法在噪声对消、信号处理方面应用得较为广泛。该算法由Hoff和Windrow等提，具有计算简单，应用较为容易等特点。然而，传统的LMS算法在收敛速度快时稳态误差较大，而在低稳态误差时收敛速度较慢。解决该问题的方法是，将传统的LMS算法定步长改为变步长，通过分析比较，选择双曲余弦函数并做变形以约束改进LMS算法的变步长。在雷达自适应旁瓣对消中使用后，有效解决了这一问题。

1 旁瓣对消技术原理

一个自适应旁瓣消除系统由一个高增益雷达天线(称为主天线)和一个或多个低增益天线(称为辅助天线)组成。根据最小均方误差准则或最大信噪比准则在不同方向接收到的干扰实时调整辅助天线的相位和幅度加权，每个辅助天线减去主天线接收到的干扰，并在干扰方向上形成一个零点，从而完成对干扰的抑制。对消原理如图1所示。

旁瓣对消技术的原理可以简单理解为主天线接收到的信号与辅助天线接收到的干扰信号作差相消。设为主天线接收的信号；=[,,…]为辅助天线接收到的信号；=[,,…,]为加权系数；为对消输出，用数学表达式可以表示为

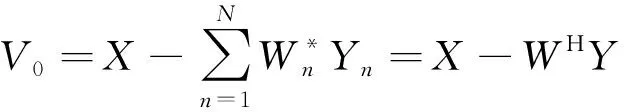
(1)

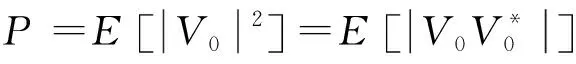
(2)

其中={×}，={×};{·}表示统计期望;表示伴随矩阵。要使值最小,需要对式(2)求导得

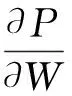
(3)

得

=×

(4)

当式(3)中的自相关矩阵为非奇异阵时，可表示为

=

(5)

这样，对消剩余功率的最小值为

=-

(6)

由式(6)求出的最优权值，能保证干扰对消的剩余功率最小。

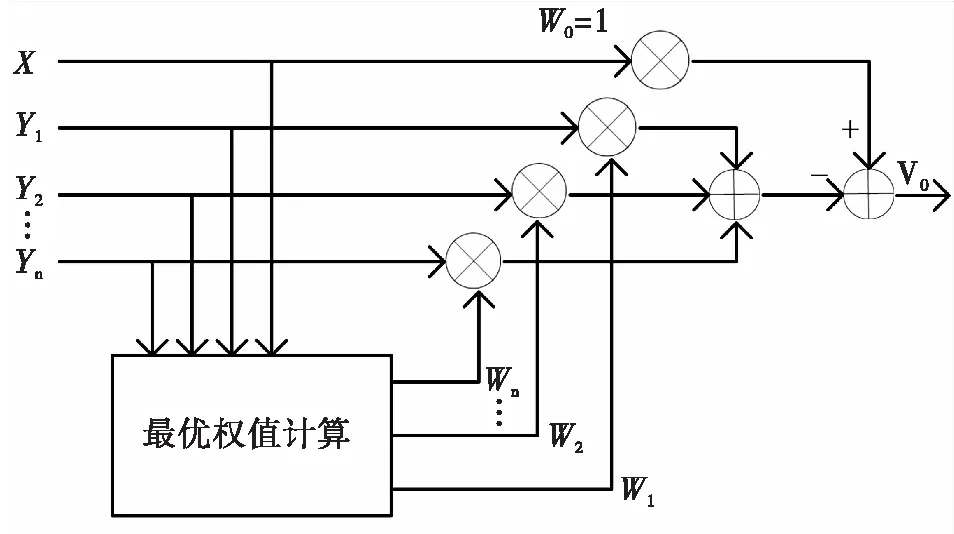
图1 雷达自适应对消原理图

2 改进LMS算法原理

LMS算法的基本原理为

()=()()(输出信号)

(7)

()=d()-()(误差信号形成过程)

(8)

(+1)=()+2()()(权值更新过程)

(9)

其中()定义为输入信号；()定义为输出信号；()为期望信号；()为误差信号；()为权值向量；为步长因子。定步长的 LMS 算法中计算权值时存在收敛速度和稳态误差相矛盾问题，即使用较大的步长会使得稳定性差，而较小的步长则会导致收敛速度过慢。针对以上问题，本文提出了一种基于双曲余弦函数的变步长LMS算法，当算法刚开始进行运算时，选择大步长以此来提高收敛的速率，在对消快结束时，选择小步长以此来减小稳态误差。双曲余弦的表达式为

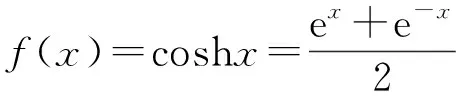
(10)

根据表达式(10)加入调整系数、、用来控制函数图形的大小，修改后的函数表达式为

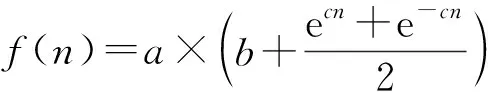
(11)

其中为误差信号()；()步长为，现在对修改后的()进行仿真以选择合适的参数。

首先保持，不变，改变的值进行仿真，仿真结果如图2所示，由于的取值不同，步长的初始值有所差异，越大步长初始值越大，滤波器收敛得越快，但是在误差即()趋近于0时依然保持较大值，这会影响稳定性能，增大稳态误差。

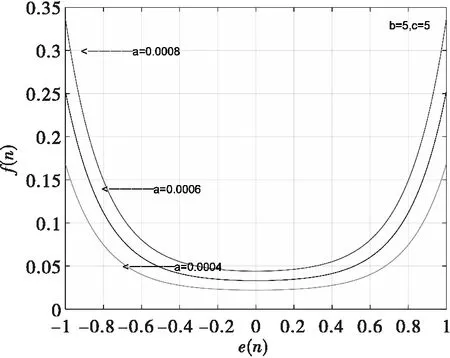
图2 不同a值对应的e(n)与f(n)关系

其次保持，不变，改变的值进行仿真，仿真结果如图3所示，由于的取值不同，步长的初始值略有所差异，步长的稳定值差异较大，这个值决定了步长的最终范围，越大稳定后步长越大，滤波器稳定性越差，这也会影响稳定性能，增大稳态误差。

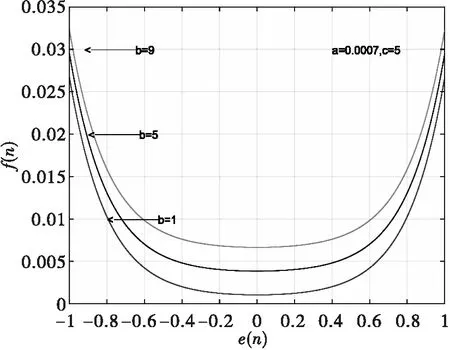
图3 不同b值对应的e(n)与f(n)关系

最后保持，不变，改变的值进行仿真。仿真结果如图4所示，可以看到由于的取值不同，初始值有所差异，越大步长的初始值越大，收敛越快但在误差趋近于0时步长变化较大，这会增大稳态误差。而越小会导致步长的初始值越小，这样会降低收敛速率。由此可以得知，需要根据实际情况选择合适的参数。

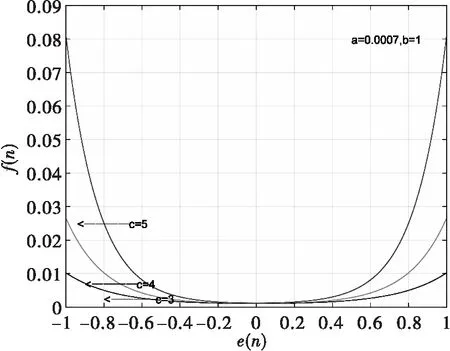
图4 不同c值对应的e(n)与f(n)关系

3 仿真分析

用仿真软件进行自适应旁瓣对消仿真，旁瓣对消系统采用本文提出的改进步长LMS自适应滤波器，设仿真中传统算法固定步长为 0.002，本文算法参数选为=0008，=5，=6，步长与误差函数关系如图5所示。

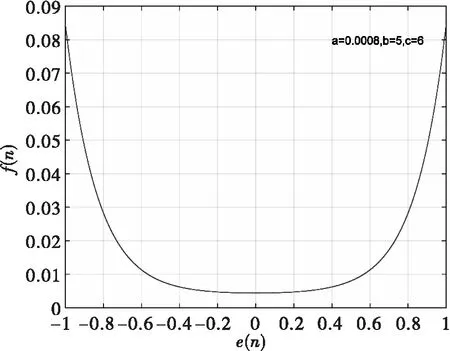
图5 本文所选参数e(n)与f(n)关系

不考虑接收机内部噪声，对主天线输入加噪的正弦信号，对辅助天线输入相同的噪声信号，用固定步长算法和本文提出的基于双曲余弦函数的变步长算法进行仿真。观察改进的LMS算法的应用性能。仿真结果如图6所示。

从仿真图中可以看出，与固定步长LMS算法相比，本文所提出的算法在稳态误差、收敛速度上都要优于传统算法。为了更加全面研究对消的性能，需要考虑到改善信噪比的大小，仿真进行了信噪比的计算，结果如表1所示。

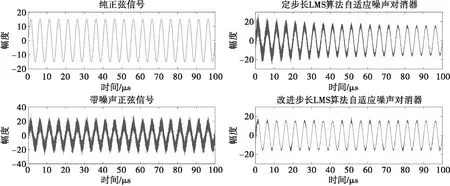
图6 改进算法对消结果对比图

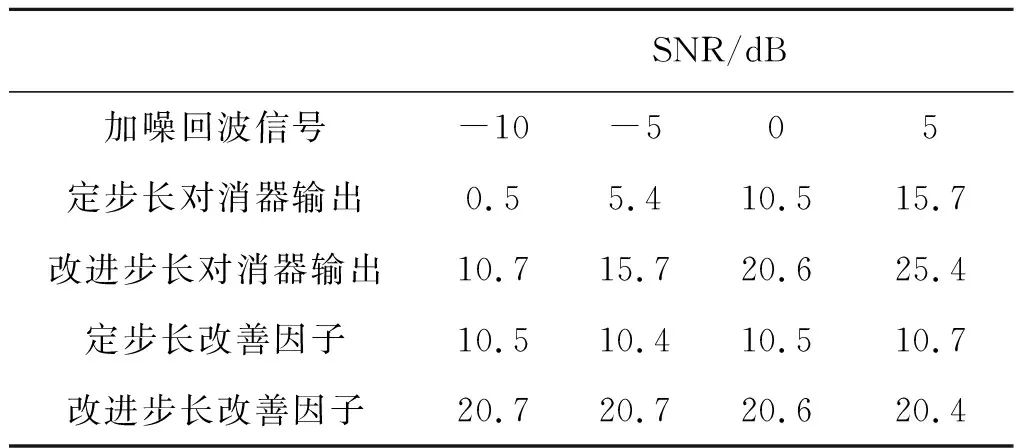
表1 不同加噪回波信号对应对消处理信号信噪比

可以看到对消器对于信号的信噪比有明显的改善，定步长LMS算法的改善因子约为10.5 dB，改进步长LMS算法的改善因子约为20.5 dB，计算过程相对简单。由此可以得出，本算法的可行性较强。

4 结束语

综上所述，本文所提出的算法可以解决传统固定步长算法的收敛性与稳定性所存在矛盾，同时将该算法应用于雷达旁瓣对消中，进行仿真对比，不仅得到了较好的对消效果，有效地提高了收敛速度和稳态性能，也提高了信噪比，而针对不同调制类型的信号，需要选择不同的参数以保证对消器最佳的性能。