基于区域封控扩展的巡飞弹集群航路规划改进方法

朱昊天，刘 星，马国军，李思远，甘延湖

(1 西安工业大学兵器科学与技术学院，西安 710021; 2 西北工业集团有限公司，西安 710043)

0 引言

巡飞弹是导弹与无人机相结合的产物，因巡飞弹续航时间有限，在实际执行任务时希望巡飞弹或巡飞弹集群在确定的时间内对地具有最大的封控区域。所以基于巡飞弹集群封控区域扩展的航路规划策略成为重要的研究问题。

完成巡飞弹集群区域封控扩展航迹规划，大致有如下几种方法：1)根据传统蚁群算法信息素挥发系数增加自适应信息素挥发因子来改变挥发速率或更新信息素规则进行改进的规划方法；2)利用三维空间模型，通过对信息素初始化过程的修改，对启发函数的影响因素、对信息素的更新机制加以改进，并完成三维路径规划仿真的方法；3)针对矩形区域对“Z”字形封控搜索算法进行改进，提高封控搜索效率的方法。目前多数学者针对传统蚁群算法中的信息素挥发因子进行改进并针对矩形区域进行封控搜索。但在实际战场环境下，目标区域边界并不一定是直线，有必要对圆形的目标区域进行研究。

针对上述问题，通过对基本蚁群算法进行优化及对传统“Z”字形覆盖搜索算法进行改进，通过在封控相同区域所用时间缩短来提高封控效率。由于传统“Z”字形区域封控搜索方法在进行区域封控时会受巡飞弹最小转弯半径限制，为保证搜索完成后无搜索死角，巡飞弹需从封控区域外进行转弯，这样的封控搜索路径长度也将增加，造成巡飞弹集群的封控资源浪费，降低巡飞弹集群封控效率。改进优化传统蚁群算法，使算法的寻优能力和收敛速率都具有更加突出的优势，在提高算法收敛速率的同时也能防止算法进入局部最优，并能找到更优质量的路径。通过改进和优化巡飞弹的转弯时机和地点，对传统的覆盖方法进行优化，可以更好对目标区域进行封锁。

1 巡飞弹区域封控航迹规划分析

1.1 蚁群算法的数学模型

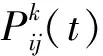
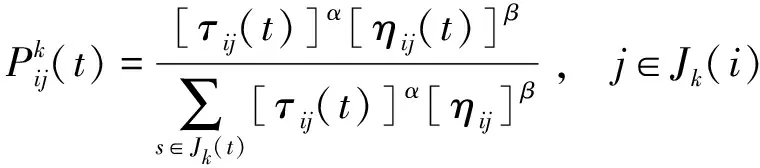
(1)

随着算法运行时间的增长，算法中的信息素含量将会像大自然中的信息素含量一样挥发。算法将会通过迭代更新路径上的信息素含量来实现这一点。路线中的信息素含量的状态信息可通过路径中的信息素蒸发系数和此次迭代路线节点中的信息素增量Δ来描述：

()+1=(1-)()+Δ, 0<<1

(2)

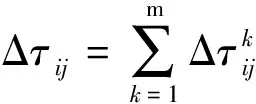
(3)

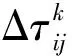
第只蚂蚁走过的总路程用来表示，增强系数为。当人工蚂蚁经过节点到节点时：

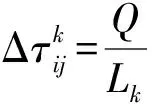
(4)

1.2 巡飞弹集群区域封控问题描述

巡飞弹执行区域封控时目标区域一般为不确定环境，即对目标区域内目标位置信息或障碍物完全未知或仅知道部分信息的搜索环境。以圆形目标区域为例，目标区域内的目标个数与位置和障碍物信息均为未知状态。假设巡飞弹集群中每一枚巡飞弹型号、性能都完全相同，枚巡飞弹在一定高度以相同速率航行，巡飞弹集群中各巡飞弹的探测半径最大为，而巡飞弹集群中各巡飞弹的转弯半径最小为，且>。文中研究目的是设计一种区域封控搜索策略，以尽可能少的巡飞弹尽快完成对封控区域内所有区域的封控搜索任务，从而实现封控区域的扩展。

2 改进巡飞弹区域封控策略

2.1 改进蚁群算法

为了扩大蚂蚁搜索路径的规模，增大未知路线被选择的几率，但又不能减缓收敛速率，对于信息素增量很难找到一个合适的参数去满足以上两点，提出了一种自适应信息素增量因子，该因子可自适应调整其大小来调整信息素的增量，从而控制各条路线中信息素的含量。的取值范围取[1，2]，将信息素增量因子的初始值设置为105，若在连续5次迭代中相邻两次的最优解的差值小于等于01时，可自动调节为原来的11倍，当的取值大于16时，强制设置的取值为16，若连续5次迭代相邻两次最优解差值小于01时，=11；若≥16时，=16。

由于约束条件的设定，既可以防止信息素增量过小导致节点间各个路径信息素差异较小，蚂蚁在搜索时对多条路径充分搜索导致收敛速度降低，又可以防止信息素增量过大导致节点间信息素差异较大，蚂蚁在封控搜索时陷入局部最优的问题。基于以上分析，改进后的蚁群算法流程图如图1所示。

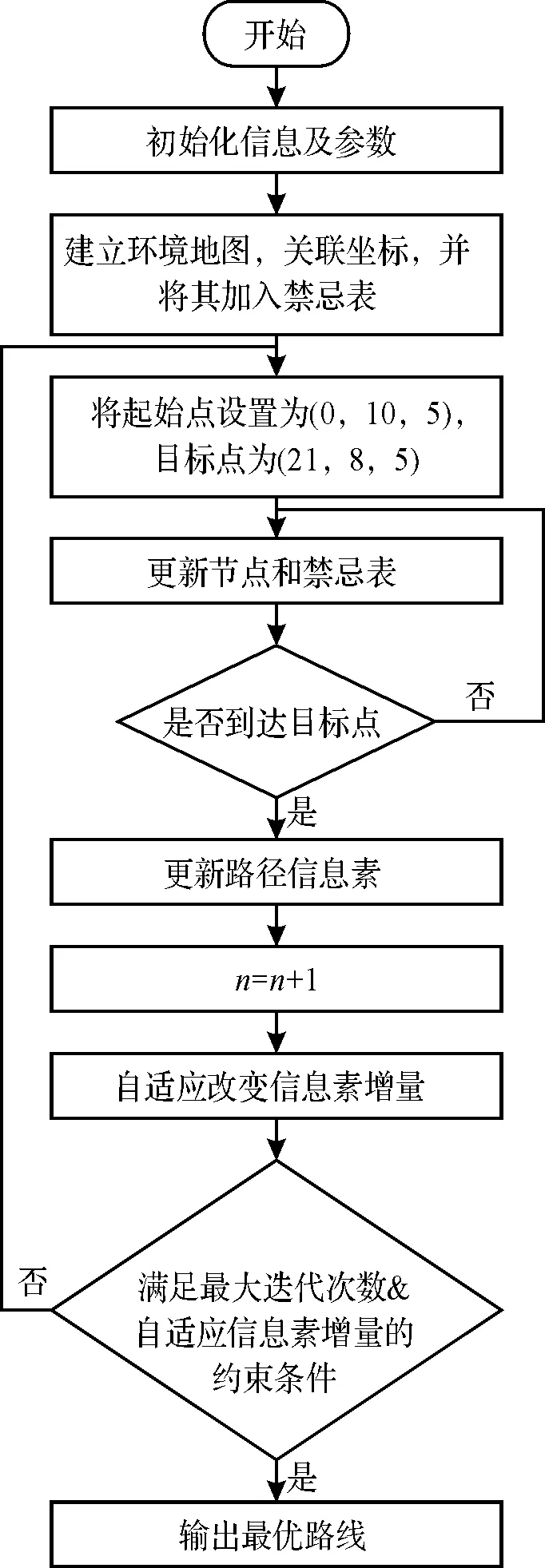
图1 改进后蚁群算法流程图

2.2 改进封控搜索模型

假定搜索区域如图2中圆形区域所示。，图中，,…,和,,…,分别为两枚巡飞弹的航迹点。

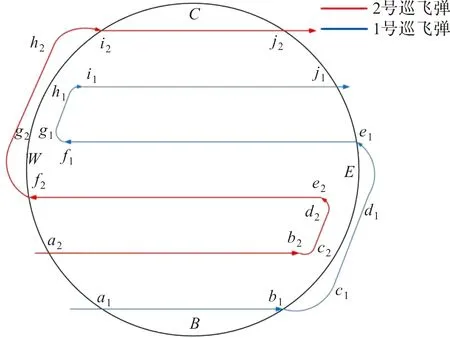
图2 改进后航迹规划示意图

建立一个半径为的圆形目标封控区域，区域封控起点选取目标区域的点，并对巡飞弹集群进行编号(编号方式为从下方到上方按1,2,…,；)枚巡飞弹组成的巡飞弹集群从目标区域的点开始排成一排执行巡飞任务，速度方向为水平向右，从到所在直线距离圆形目标封控区域下顶点为。集群中每相邻两枚巡飞弹之间的距离为2，故巡飞弹集群的搜索宽度为2。

当1号巡飞弹抵达点后，将沿以最小转弯半径向左方转弯，经过到后继续沿直线飞行，后沿向左方转弯飞行；为了提高区域封控搜索效率，从而实现对封控区域的扩展，故规定除1号巡飞弹外其他巡飞弹不必到目标区域的右边界再进行转弯，只需当号巡飞弹抵达点时，以最小转弯半径经过到到飞行，假设距离右边界的长度为，可得：

=(-1)(-)=2,3,…,

(5)

在图2中距离目标区域右侧边界的长度为=-。故1号巡飞弹在转弯过程中飞行路径长度为：

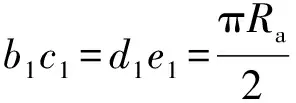
(6)

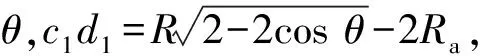
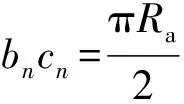
(7)

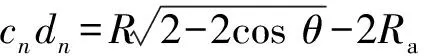
(8)

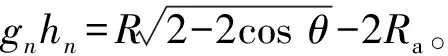
=(-)(-)=1,2,3,…,-1

(9)

巡飞弹集群中的1号巡飞弹将最后完成向右方转弯，此时，集群中各巡飞弹重新组成一排从左至右进行搜索。重复以上，知道巡飞弹编队完成对目标区域的封锁。

假定巡飞弹集群编队完成区域封锁搜索时，巡飞弹集群刚好停留在目标区域右上边界上，如图2所示，以两枚巡飞弹为例，第二枚巡飞弹与目标区域点的距离为。在相同区域内，传统搜索方法航迹长度为：

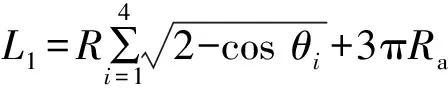
(10)

结合图2，改进后的巡飞弹搜索航迹为：

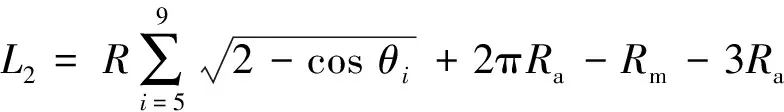
(11)

由于>，>，>，>，显然>，经理论分析可得改进后的区域封锁算法整体路径长度小于传统“Z”字形搜索策略，从而实现对封锁区域的扩展。

3 仿真验证与分析

为了验证对传统算法改进的有效性，用MATLAB进行仿真试验，并将结果与传统蚁群算法加以比较。

设定空间大小为21 km×21 km×2 km，其中轴，轴方向每个节点之间的距离为5 km，轴方向每个节点之间的距离为500 m。设置路径起点，在空间中的坐标为(0 km,10 km,5 km)，目标点坐标为(21 km,8 km,5 km)。

通过设置相同参数，与传统蚁群算法仿真结果图对比如图3所示。其中，图3(a)为传统蚁群算法航迹规划；图3(b)为传统蚁群算法最佳适应度值、迭代次数曲线图；图3(c)为改进后蚁群算法航迹规划；图3(d)为改进后蚁群算法最佳适应度值、迭代次数曲线图。

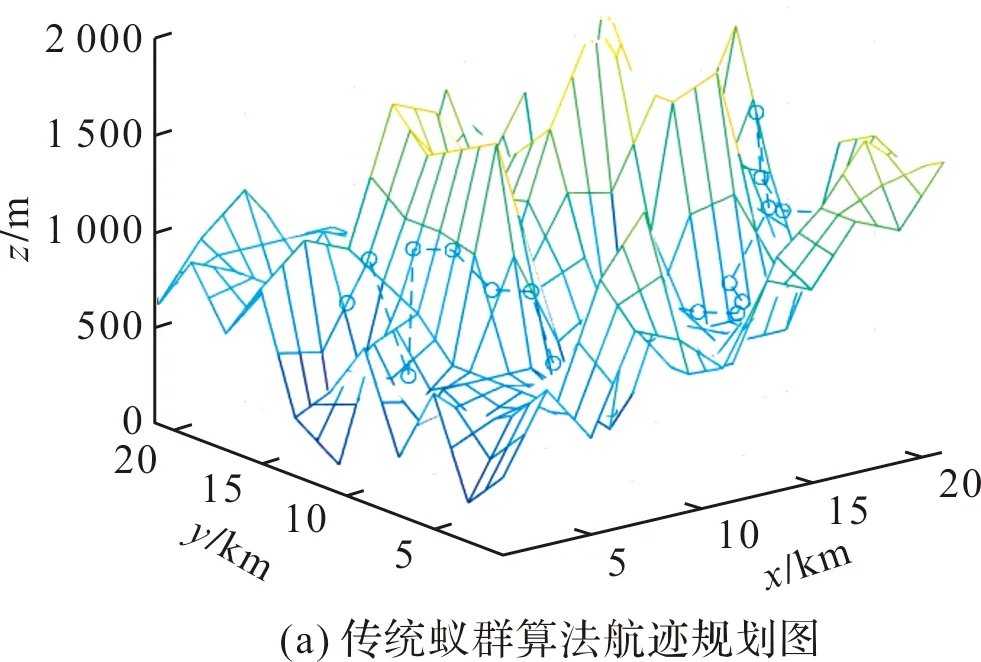
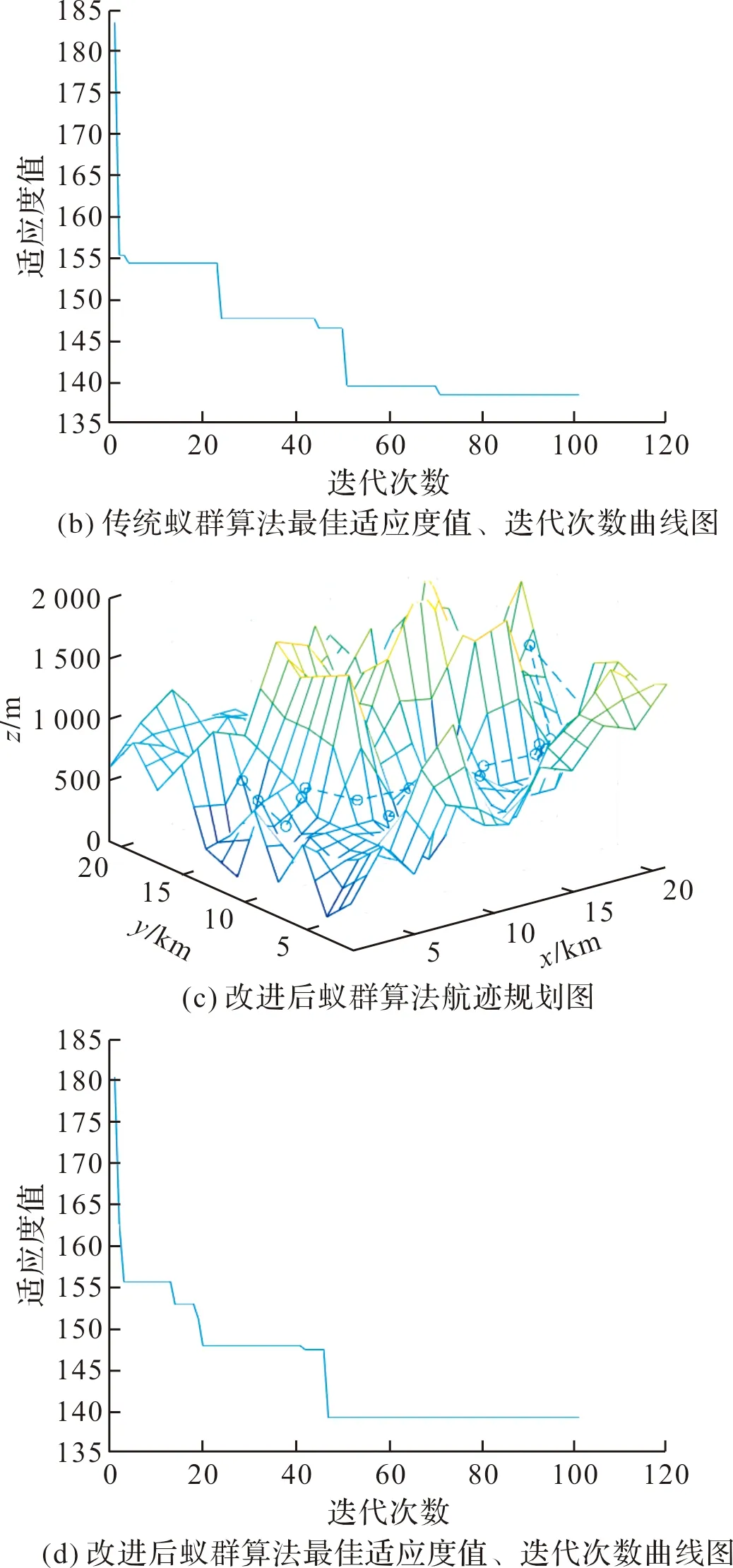
图3 与传统蚁群算法仿真结果对比图

通过对图3的最佳适应度值、迭代次数曲线的研究发现，改进后的蚁群算法可以在获得最优解的同时，迭代次数也得到一定的减少，从而证明了对蚁群算法的改进是可行的。为保证结果的准确性，分别运用本文改进算法与传统蚁群算法进行多次试验，随机抽取3组试验结果，如表1所示。

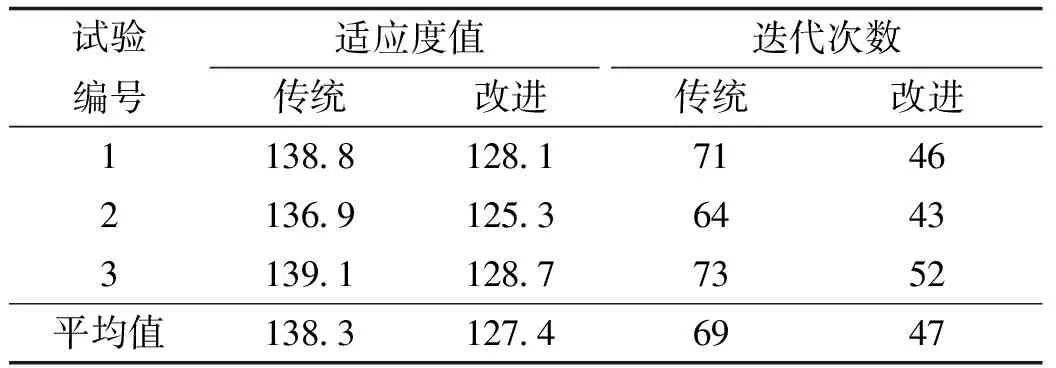
表1 适应度值、迭代次数对比表

从试验结果可以发现，经过优化后的最佳适应度值有了显著下降，且迭代次数也显著下降，从而证明了自适应信息素增量因子能增强蚁群算法搜索最优解的能力，同时可以有效解决传统蚁群算法收敛速率较为缓慢，且很容易会进入局部最优的缺陷。

为了验证改进区域封控搜索算法的有效性，设置如下目标区域的初始条件：=20 km，=0.1 km/s，=2。用若干个1×1网格来表示目标封控区域，并对每个网格赋初值为1，如果有某个网格被巡飞弹集群中的某枚巡飞弹搜索过时，则将该网格赋值为0。因此可用每个网格赋值之和的降低情况来表示区域封控搜索算法的搜索效率与效果。将改进区域封控搜索算法和传统“Z”字形搜索进行对比仿真。改进后的搜索算法搜索轨迹如图4所示。两种搜索方式仿真对比如图5所示，对目标区域的封控任务两种方法均可有效完成，但随着区域封控搜索任务的逐步完成，改进区域封控搜索算法的优势逐渐显现出来。从250 s附近开始，巡飞弹编队开始转弯，由于改进封锁算法减少了转弯过程中无效搜索的面积，故其封锁效率逐渐优于传统“Z”形搜索方法。此外，遇到转弯时，传统“Z”形搜索方法总剩余封锁价值显示的降低速度有一个明显的减缓过程，而改进的封锁算法则不明显。

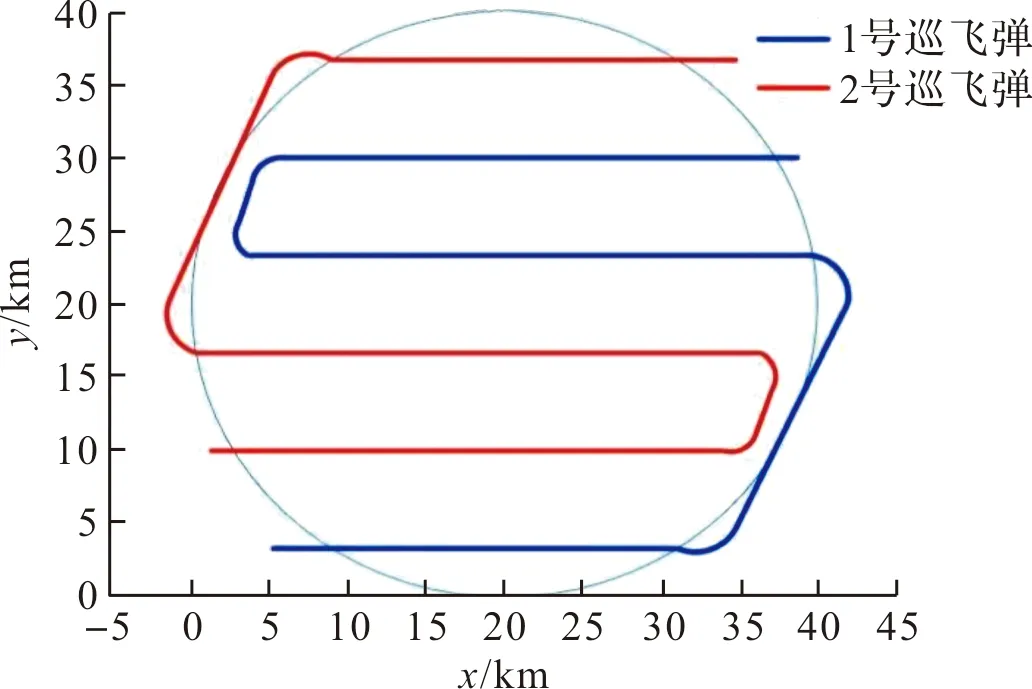
图4 改进搜索算法搜索轨迹图

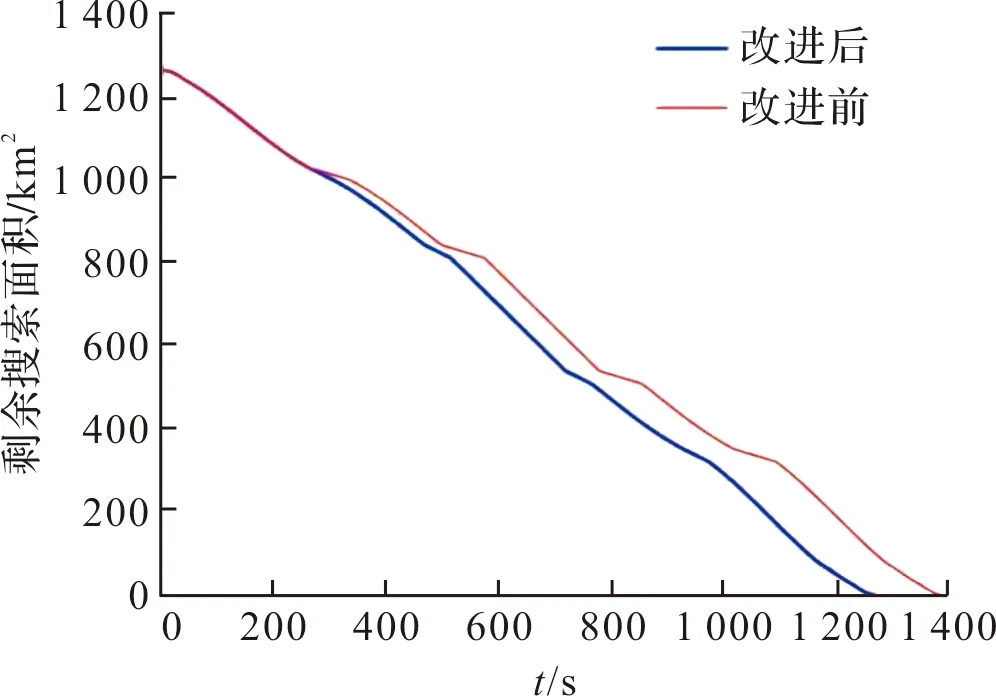
图5 两种搜索方式仿真对比图

由仿真结果可以看出，经过改进的封锁算法用时最短，即同等时间改进的封锁算法可以封锁更大区域，巡飞弹集群封锁效率明显提高，所得结论与理论分析一致。

4 结论

在环境信息未知情况下，通过加入一个自适应信息素增量因子对传统蚁群航路规划算法进行改进，并对巡飞弹集群转弯时机和转弯半径进行修改，由理论分析与仿真验证了所提出的改进方法不仅优化了单枚巡飞弹航迹规划路径长度和迭代次数，而且提高了巡飞弹集群封锁搜索效率，具有较强的实用性。但对不规则目标区域进行封控时，改进后的“Z”字形搜索算法可能还存在一定局限性，需要进一步研究。