基于势博弈的多QoS无人机基站空间优化部署
2022-10-12芦方旭米志超马骏李艾静王海
芦方旭,米志超,*,马骏,李艾静,王海
1.陆军工程大学 通信工程学院,南京 210007 2.中国电子科技集团公司第二十八研究所,南京 210007
随着第五代(5G)移动通信技术的普及,万物互联的时代悄然而至,如今,物联网(IoT)中需要连接的设备数量呈爆炸式增长,预计至2030年,全球IoT设备的数量将达到惊人的800亿台,基于此,泛在网的发展要求更多的基站部署,但诸多现实困难滞缓了地面基站的建设,特别是在运营成本居高不下的偏远地区和遭遇自然灾害导致基站损毁的受灾地区。
无人机由于其灵活性强、部署迅速、视距信道(LoS)的高鲁棒性等优点,将通信单元安装在无人机上,构成无人机基站,可以提供紧急通信服务。与地面基站相比,无人机基站可以在极端环境和复杂地形下使用,其优异的灵活性与机动性,可以快速部署到目标区域,例如今年河南省暴雨造成的通信阻隔,通过一架固定翼无人机提供紧急通信服务,这让无人机基站的紧急覆盖通信逐步成为现实,但单机的覆盖时间有限,区域较小,固定翼无人机基站无法悬停且造价高昂。试想采用造价更加低廉的多架旋转翼无人机基站来实现覆盖区域更大,更加灵活的本地按需部署。但在同一区域部署过多无人机基站,一方面会造成资源的浪费,特别是在应急救灾的环境中,多一架无人机基站就可以连通一大片区域的受灾群众,这对安定人心就有重要意义;另一方面从通信效果来看,过多的无人机基站部署在同一片区域,会造成相互的干扰,相互的影响之下,反而造成通信效用降低,影响接入的用户。因此需要采用一种更加快速高效的方式来实现合适数量的无人机基站的部署。
在目前对无人机基站的研究中,文献[4]对无人机进行地空路径损耗建模,建立了视距(LoS)链路和非距线(NLoS)链路的通信模型;文献[5]推导了单个无人机基站在空间部署时,满足通信阈值条件下的最佳部署高度;文献[6]主要研究了存在同频干扰时2个无人机基站的最佳部署距离来最大化覆盖范围;文献[7]采用通过改进的遗传算法来实现三维空间部署单个无人机基站,旨在最大化覆盖用户数量;文献[8]研究了多个无人机基站在热点区域采用k-means算法来寻找的无人机三维空间的最佳覆盖位置。博弈论比起其他带约束条件的传统方法,更加便于理解和分析,因此也广泛应用于无人机领域。文献[9]把无人机建模为享乐博弈(Hedonic Game)的合作模型去找寻任务分配的纳什均衡点,但是享乐博弈需要更多时间才能到达所有无人机的纳什均衡点;文献[10]中使用的是非合作博弈模型,最后也能取得竞争关系的平衡,但该方案不适用于所有类型的无人机网络;文献[11]使用博弈论建模无人机基站覆盖问题,研究了在多无人机基站的覆盖,发生无人机基站故障时,快速恢复覆盖通信的能力。
与之前工作不同之处在于,根据局部互利博弈的相关定义,证明了无人机基站部署符合势博弈模型,并且在纯启发式算法的基础上,提出一种基于势博弈的超启发式算法,用来求解多无人机基站满足用户不同QoS需求下的所需的最少无人机数量以及快速覆盖部署问题。
本文的主要工作如下:
1) 在满足最高通信阈值的要求下,使用Karush-Kuhn-Tucker(KKT)条件计算出无人机基站的最大覆盖半径、最佳高度。
2) 证明无人机基站部署是势博弈过程,该过程至少具有一个纳什均衡(Nash Equilibrium,NE)点,并且该纳什均衡点是全局或局部最优解。
3) 在第一步最大覆盖半径的基础上,计算理论上所需无人机基站数量的下限值,采用基于势博弈的超启发式灰狼算法(Hyperheuristic Gray Wolf Optimize,HGWO),通过迭代来逼近无人机基站最大覆盖要求下的纳什均衡点,实现无人机基站的最优部署,若能全覆盖地面用户,此为全覆盖用户要求的最少无人机基站数量,如若不能,增加无人机基站数量。
1 系统模型与问题描述
1.1 系统模型
考虑在复杂地形环境下发生战争或者自然灾害,地面基站损毁,目标区域内密集分布各种通信设备,紧急部署无人机基站,对地面所有用户提供通信服务,目标是要实现尽可能少的无人机基站覆盖地面用户,系统模型如图1所示。

图1 系统模型图Fig.1 System model
对用户接收功率建模,用户的接收信号功率′由视距连接和非视距连接2部分组成,具体表示为
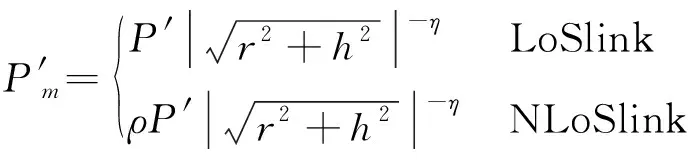
(1)
式中:′为无人机基站的发射功率;为用户到无人机基站链路上的路径损耗指数;为由于非视距连接而产生的附加衰减因子;为用户到无人机基站水平位置投影点的距离;为无人机基站的垂直高度。
采用地空信道模型,LoS传输的概率和仰角的表达式为
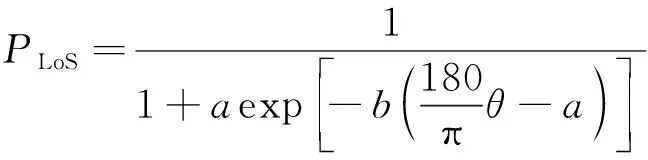
(2)

(3)
式中:、是由环境决定的路径损耗参数。NLoS传输的概率为=1-。
由式(1)和式(2)可以得到用户的接收功率为


(4)
用户的信干噪比(Signal to Interference plus Noise Ratio, SINR)可表示为
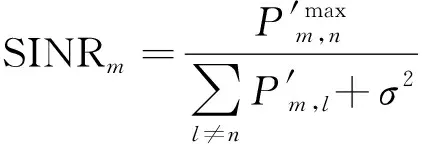
(5)
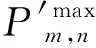
假设所处区域的用户存在个不同的服务质量(Quality of Service,QoS)需求,即用户的通信阈值存在个不同的值,只有满足SINR≥时,用户与无人机基站连通,为不同QoS需求用户的通信阈值。因此构造指示函数,表示为

(6)
即当用户被无人机基站覆盖时,,=1,否则,=0。
无人机基站覆盖通信的用户数量可表示为

(7)
式中:表示部署区域的用户总数。
目标区域内,个无人机基站通信覆盖用户数量为

(8)
1.2 问题描述
优化目标是用尽可能少的无人机基站覆盖整个区域,即用最少的个无人机基站覆盖个不同通信阈值的个用户。该优化问题表述为

(9a)
s.t.
=
(9b)
,∈{0,1}, ∀∈,∈
(9c)

(9d)
≤≤
(9e)
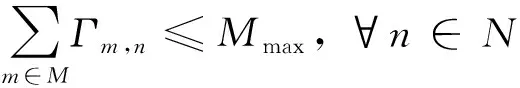
(9f)
SINR≥, ∀∈,∀∈
(9g)
约束条件(9b)表示目标区域内个用户被基站全覆盖;约束条件(9c)指定了指示函数的取值范围;式(9d)表示任意用户至多与一个无人机基站连通;约束条件(9e)是对无人机的部署高度进行限制;约束条件(9f)表示单个无人机基站覆盖的用户数量要小于无人机基站允许连通的最大用户数量;约束条件(9g)表示,满足被无人机基站的覆盖条件是接收信干噪比要大于通信阈值。
2 解决方案
2.1 计算最少无人机基站数量的下限值
用和分别表示无人机基站的覆盖半径与部署高度,优化目标是用最少的无人机基站进行目标区域的覆盖,当无人机基站的覆盖半径最大时,部署的无人机基站数量最少。求解满足用户通信阈值的单个无人机基站最大的覆盖半径,该问题可以表示为

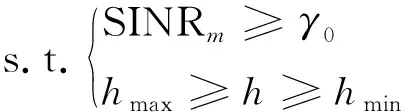
(10)
把P2问题简化,用户的不同通信阈值统记为,使用KKT条件来求解该约束条件的最优化问题。因此结合式(3)该问题可以转化为

为了表述简单,定义以下变量来表述函数
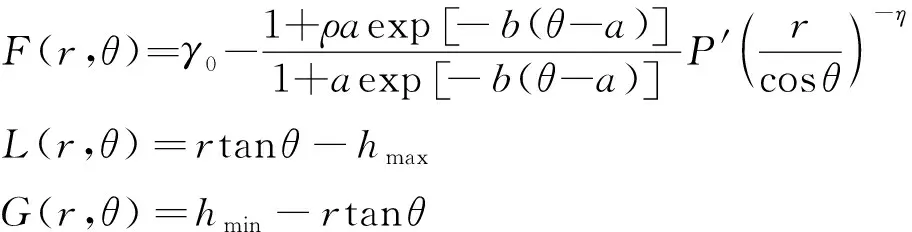
根据KKT条件,参数需要满足以下条件:

利用KKT条件分类讨论求解,可以得到

(11)
此覆盖半径是理论上的最大覆盖半径。
2.2 无人机基站部署的博弈模型
用最少的无人机基站进行目标区域的覆盖,就必须要确保给定的无人机基站放置在最佳部署位置。因此首要解决的问题是给定无人机基站来快速寻求最大覆盖用户的部署位置,该问题可以表示为
P4: max
s.t.
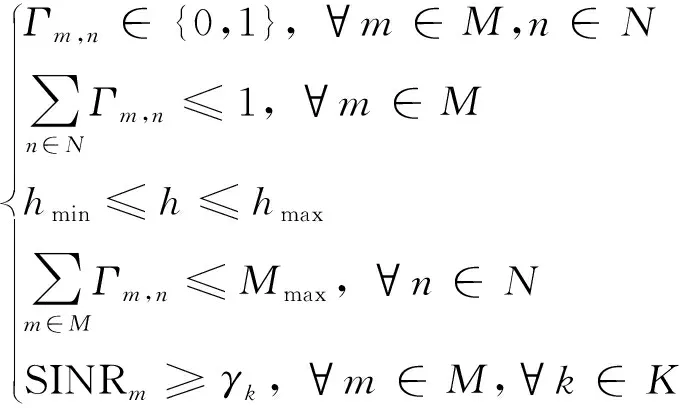
(12)
为了解决最大覆盖问题,无人机基站的部署使用博弈论建模,将模型记为={,,},其中:是部署的无人机基站;是无人机基站部署位置合集,分为近点与远点,近点是无人机基站在周边的27个位置,简单描述为{原点、前、后、左、右、上、以及各自的对角位置};远点表示无人机基站的全局搜索位置,以更远的部署为远点。如图2 所示,红色小球表示无人机基站的当下位置,五角星所在的空间位置表示近点位置,其余空间表示远点位置。是效用函数,定义为任意基站和其相邻基站的覆盖用户数:
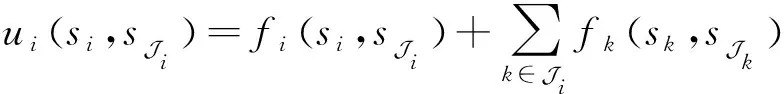
式中:J表示无人机基站的相邻无人机基站的集合;(,J)=,∀∈,即(,J)表示无人机基站的覆盖用户数。相邻无人机基站即两无人机基站的中心位置在水平方位的距离小于基站的最大覆盖范围。

图2 无人机基站部署位置示意图Fig.2 UAV-BS deployment location schematic
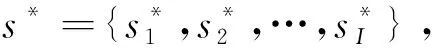


如果存在一个势函数对于任意的参与者的状态由变为′若满足
(′,-)-(,-)=(′,-)-(,-)
则该博弈称为精确势博弈。即势博弈中任意参与者单方面改变策略导致的效用函数变化量等于势函数的变化量。
无人机基站的部署模型是一个精确势博弈,至少有一个纳什均衡点。
构造势函数
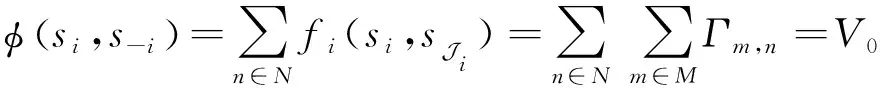
式中:-表示除参与者之外的其他参与者的状态集合;势函数(,-)为式(8)表示的整个区域的无人机基站的覆盖数量。
在无人机基站的状态集合中,任意无人机基站的部署位置的变化都只会影响相邻无人机基站的用户覆盖。因此,对于任意的无人机基站由位置变为′,势函数的变化为
(′,-)-(,-)=(′,J)+


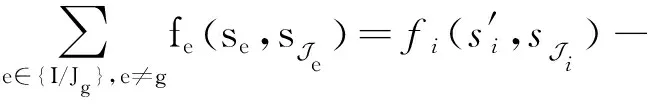

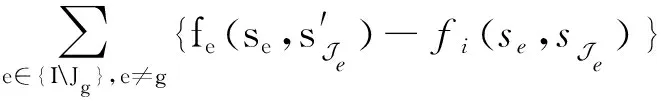
任意无人机基站的位置变动,都只会影响相邻的无人机基站覆盖下的用户,即
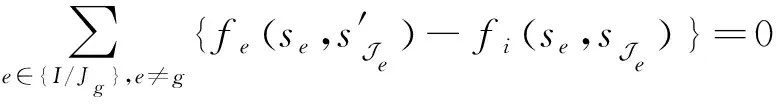
可以得出:
(′,-)-(,-)=(′,-)-(,-)
由定义可知,该过程是一个精确势博弈过程。
由势博弈的诸多性质可得,势博弈至少有一个纳什均衡点,并且该点是势函数的全局或局部最优解。
2.3 算法设计
由于无人机基站的部署还要考虑当下部署位置与相邻无人机基站的关系,相互之间存在耦合关系,所以很难求得精确的纳什均衡点。因此,本文提出一种超启发式灰狼算法(Hyperheuristic Gray Wolf Optimize,HGWO),通过迭代的方式去逼近无人机基站部署博弈的纳什均衡点,从而实现无人机基站的部署优化。
超启发式灰狼算法可以产生既适应参与者状态又适应博弈动态的策略。提出的算法的基本思路是将问题的搜索空间分为近点与远点搜索两大类扩大搜索空间,目标函数映射为博弈的效用函数,通过多次迭代来逼近纳什均衡解,同时使用启发式算法思想根据博弈的结构来动态调整选择策略,以期望用最小的代价快速求得最优解。
计算远点效用函数值,选择使用灰狼优化算法(Gray Wolf Optimizer,GWO),该算法是受到了灰狼捕食猎物活动的启发而开发的一种优化搜索方法。在野外的狼群具有一定的社会性,狼群的捕食行为主要是在首领的带领下协作完成,把众多的普通狼个体称为搜索因子,具有全局搜索的能力,主要的逼近猎物(目标函数)是由几个首领(按效用函数排序)完成的。该算法结构简单,初始搜索空间大,并且由于后续搜索空间不断减少,收敛速度快。
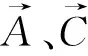

(13)
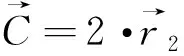
(14)
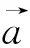
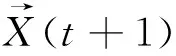

(15)
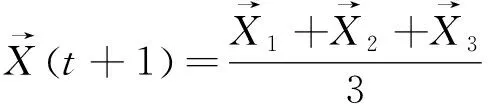
(16)

超启发式灰狼算法的概率更新公式为
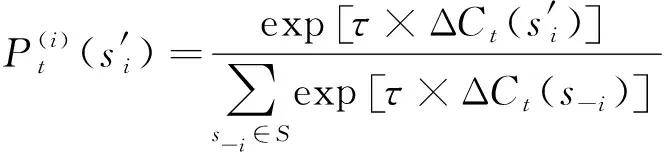
(17)
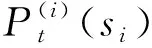

由Δ(′)的更新公式可得,只有无人机基站选择变动部署位置才会更新效用差值,否则保持不变。
具体算法框架如图3所示。实现过程如算法1所示。
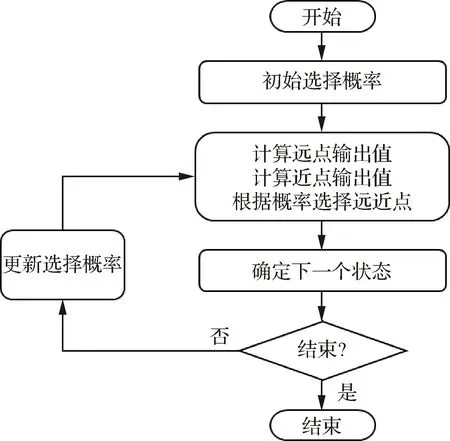
图3 超启发式算法流程图Fig.3 Flow chart of hyperheuristic methodology

算法1 基于HGWO的快速部署算法初始化 地面用户在目标区域随机分布;计算最大覆盖半径和无人机基站数量的下限M;随机生成无人机基站位置;设置迭代次数t=0。循环开始:步骤1 设置无人机基站数量为计算所需无人机基站数量的下限M。步骤2 设置迭代次数t=1。步骤3 任选一个无人机基站,对所有无人机基站依次执行步骤4 ~步骤11。步骤4 随机生成ζ个搜索代理的位置;判断选定的无人机基站和生成的搜索代理的位置是否超出区域边界,高度是否在限制条件内,若否则调整至该区域内。步骤5 搜索远点位置:用搜索代理位置依次替换无人机基站位置,分别计算效用函数ui,选取效用函数最大的3个位置标记为3个首领位置α、β、δ,根据式(16)和式(17)计算远点选择位置。步骤6 搜索近点位置:计算无人机基站的近点位置的效用函数,计算效用函数值最大的近点选择位置。步骤7 比较近点与远点的效用函数值,根据式(18)的概率选择一个部署位置。步骤8 根据式(14)和式(15)调整A→、C→2个参数;根据3个首领位置α、β、δ和最终选择的部署位置,根据式(16)更新搜索代理的位置。步骤9 调整迭代次数,t=t+1。步骤10 判断迭代次数t是否达到最大迭代次数,若是,则记录效用函数值,计算覆盖率;否则返回步骤3。步骤11 若达设置迭代次数后,此时覆盖率为1,记录无人机基站数量,循环结束;若此时覆盖率不为1,无人机基站数量设置为M=M+1,返回步骤2。
2.4 算法分析
多无人机基站的精确通信覆盖,用尽量少的通信资源取得最大的覆盖效果,这对于救灾抢险甚至是军事斗争都具有现实意义。
使用所提的超启发式灰狼算法,无人机基站的部署博弈以概率1收敛至纳什均衡点。
根据以上对超启发式灰狼算法的描述可知,任意无人机基站的效用函数在迭代过程中都是非减的。由于无人机基站部署博弈是精确势博弈,任意参与者单方面改变策略导致的效用函数变化量与势函数的变化量一样,因此整个区域的总覆盖率在迭代过程中也是非减的。而对于一个用户数量有限的静止网络,其通信覆盖数量会有上界并且是确定的。因此,使用所提的超启发式灰狼算法,多个无人机基站的部署必然会收敛至一个稳定状态,使得任意无人机基站单方面改变其部署位置无法提升其自身效用值或全网覆盖率,根据定义1,该稳定状态即为纳什均衡点。证毕。
启发式算法往往可以快速、高效地寻得一个比较好的解,但是也容易出现过早收敛,陷入局部最优解,而放弃寻找全局最优解。为了克服传统启发式算法陷入过早收敛,使用近点搜索和策略选择概率对纳什均衡点施加一定的扰动,使其偏离原纳什均衡点,接着由各无人机基站按照原搜索策略动态恢复到新的纳什均衡点。不断重复这样的扰动恢复过程直至搜寻到更优的纳什均衡点,近点搜索的扰动在最优部署位置附近扰动幅度较小,因此当扰动范围小于一定数量,根据定理2,该过程一定会最终收敛到纳什均衡点。同时由于部署区域远大于博弈探索算法中的移动探索距离,再增加全局搜索位置之后,算法收敛速度明显加快。
3 仿真结果与性能分析
本节对无人机基站的部署进行仿真分析,由环境影响的信道参数=9.61,=0.16,用户的数量为500个,共有4种不同的信道容量需求,随机分布在区域大小为4 km×4 km的目标区域内,单个无人机的最大覆盖用户数设置为80个,其他仿真参数的设置如表1所示。

表1 部分仿真参数的设置Table 1 Setting of part of simulation parameters
3.1 无人机初始化设置
在仿真的设置中,用户的通信阈值设定参考文献[17]。为突出算法的针对性,选取通信阈值较为接近的多种用户类型,来讨论无人机基站的覆盖性,设置如表2所示。

表2 用户设置Table 1 User’s settings
在目标地区部署不同QoS需求的用户,用户的位置是随机的,并且无人机覆盖用户数量也会因为不同QoS需求而不同,因此,引入松弛条件,假设该地区覆盖的用户服务质量只有一种类型,用户的最高通信阈值记为,用户的最低通信阈值记为,讨论在与下,无人机基站部署的数量。在确定通信阈值的情况下,无人机的初始高度与最大的覆盖半径如图4所示。

图4 无人机的高度与接收信噪比关系Fig.4 Relationship between height of UAV and received SINR
根据式(4)和式(12)和图4可得,影响用户接收功率的因素主要是2个,一是无人机基站到用户的仰角,进而影响到视距与非视距链路的连接概率;二是无人机基站到用户的连接距离。当无人机基站的高度较低时以视距(LoS)连接链路为主,高度较高时,以非视距(NLoS)链路连接为主,当无人机基站的高度逐步升高时,会存在主要接收信号从视距链路到非视距链路的变化,此时存在临界点,即为无人机基站的最大接收信号时的高度,因此,高度与接收信号的阈值关系即先升后降。在本节中,满足最高通信阈值的最大覆盖半径为471 m,最低通信阈值的最大覆盖半径为692 m,进而求出无人机基站的下限为9个。
3.2 不同算法空间部署示意
在模拟中,选择基于K均值的布局(K-means)算法,基于改进遗传算法的纯启发式多种群遗传算法(Multi-Population Genetic Algorithm,MPGA)、原始的灰狼算法(Gray Wolf Optimizer,GWO)作为基准方案。
K-means聚类算法对用户进行快速聚类,从使用最少无人机基站开始,检查是否满足无人机基站的服务半径和服务能力约束。如果不是,则添加一架无人机基站并重复上述步骤,直到所有用户都满足约束条件为止。
MPGA算法和原始灰狼算法采用改进的纯启发式算法,对比提出的HGWO算法,容易陷入局部最优,多次仿真求平均值后,算法性能不稳定。
图5中,地面不同颜色的符号表示不同QOS地面用户随机分布的位置,分别使用本文提出的HGWO算法、MPGA算法、GWO算法、K-means算法进行多次仿真的稳定值。红色小球表示在该算法下无人机基站的部署位置,三维空间中无人机基站在、平面的投影位置用橙色和紫罗兰色表示。本文提出的HGWO算法比起传统的GWO算法在无人机基站部署数量方面减少约18%。
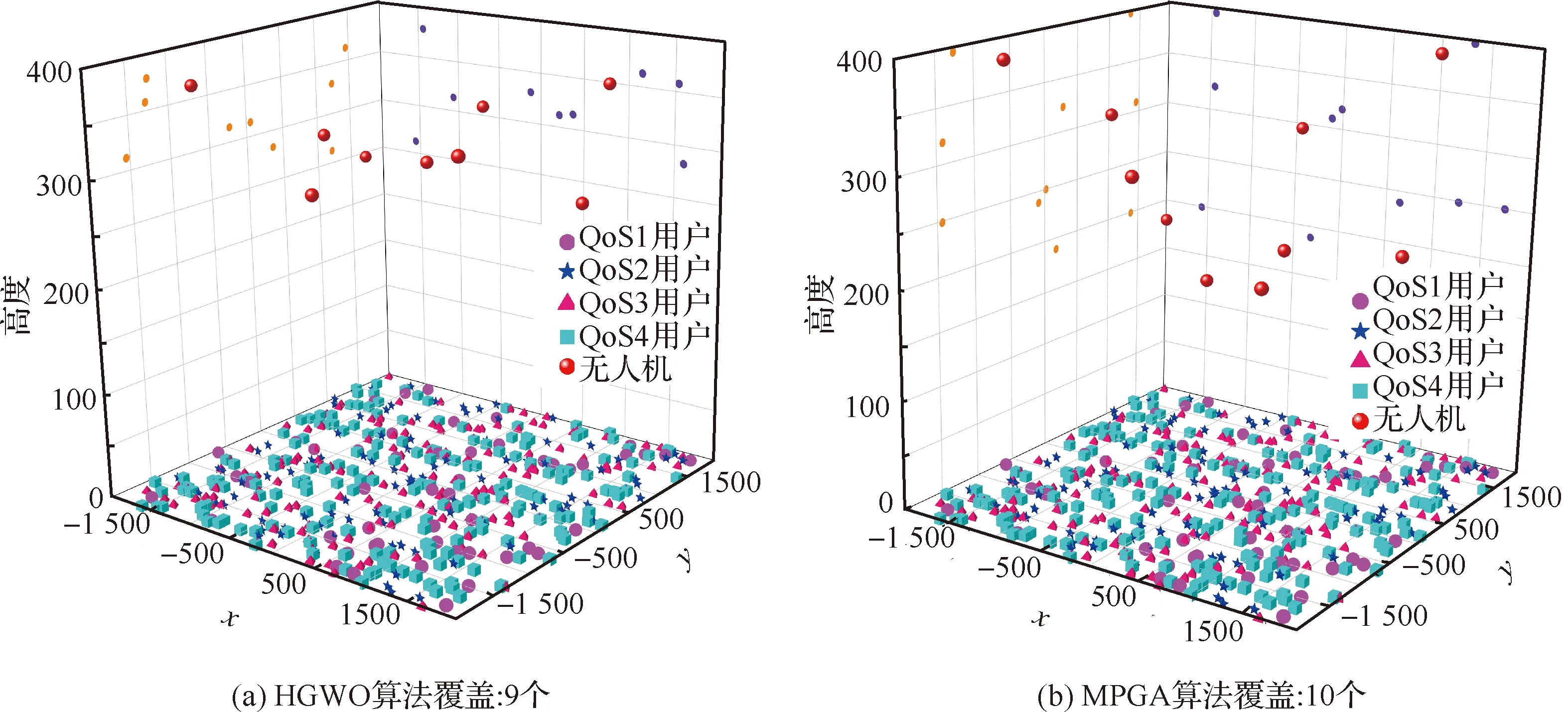
3.3 算法收敛性
图6表示9个无人机基站覆盖下的算法收敛过程,与定理2描述的一样,本文所提HGWO算法最终收敛到纳什均衡点。势博弈探索算法(Potential Game Exploration algorithm,PGE)是把无人机基站下一步的运动位置建模在周围一定距离内,通过式(17)选择动作的概率,来逐步寻找最佳部署位置。
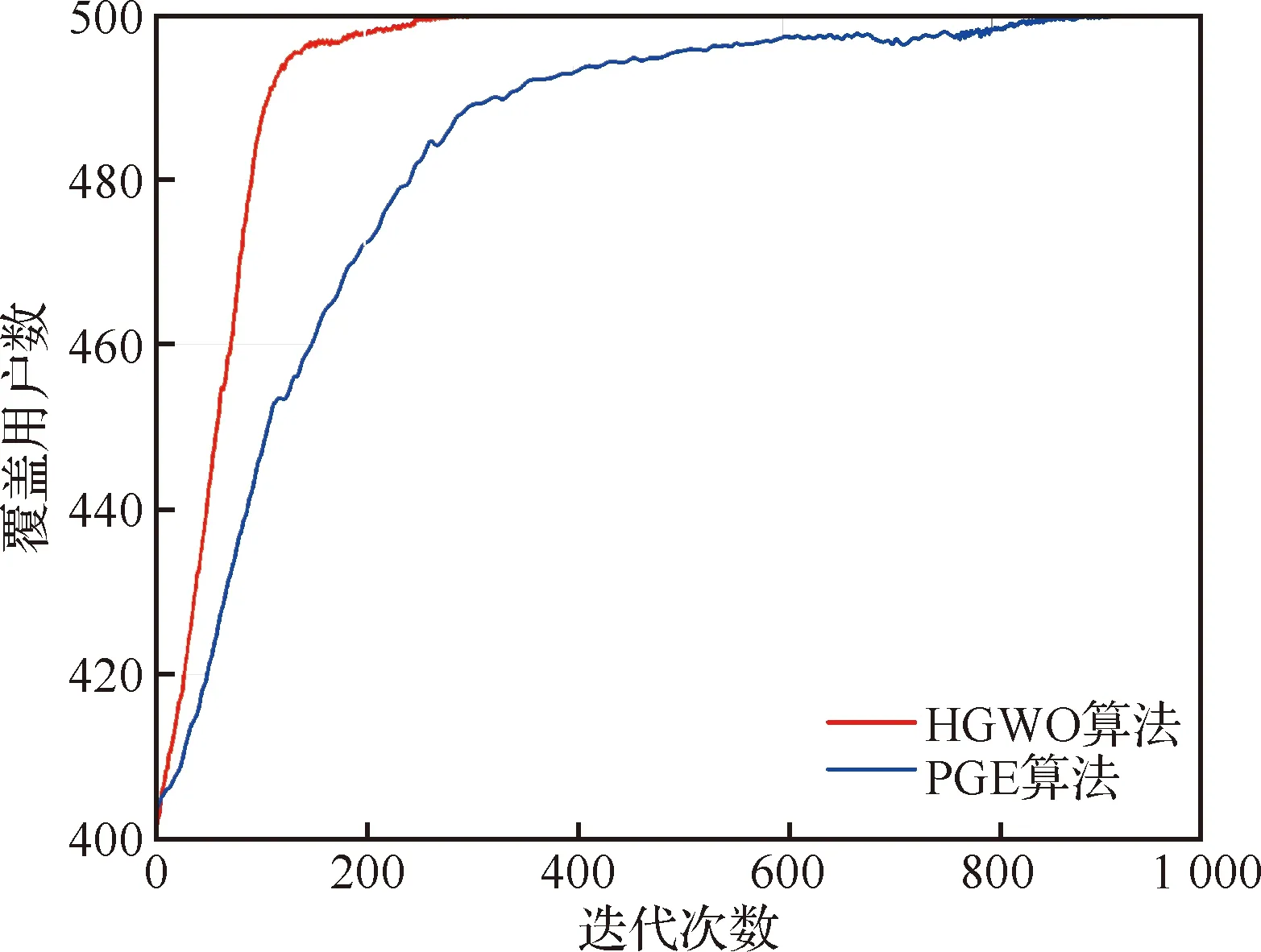
图6 算法的收敛性Fig.6 Convergence of algorithms
与本文所提HGWO算法对比,由于部署的区域远大于PGE算法中的移动探索距离,依一定概率探索选择最佳部署位置,算法的收敛速度较为缓慢,而本文所提算法,在近点周边搜索的基础上,加以启发式算法进行远点的全局搜索,算法收敛速度明显加快。
3.4 无人机基站部署数量
图7(a)表示区域长度为2 km,4种算法下覆盖用户数量变化对全覆盖所需的无人机数量的影响,当区域一定,用户数量较少时,无人机数量相对少一些,但是当用户多到一定数量时,无人机基站受到最大连通数的限制,用户数量增加,无人机基站的数量也持续增加。
图7(b)表示用户数量为500个,4种算法下覆盖区域大小对全覆盖所需的无人机数量的影响。当用户数量一定时,目标区域越小,无人机基站在允许的最大覆盖数量内,覆盖范围越集中,覆盖用户所需的无人机基站数量越接近于理论值;但随着目标区域的变大,用户分布密度变小,考虑到无人机基站覆盖半径的限制,需要更多的无人机基站来覆盖用户,覆盖用户所需的无人机基站数量与理论值之间的差距变得越来越明显。

4 结 论
考虑到用户不同的服务质量要求和无人机的接收干扰问题,以无人机作为通信基站,为地面用户提供服务,求解全覆盖用户的条件下最少无人机基站的最优部署问题。首先,通过KKT条件求解满足通信阈值的无人机的最大服务半径;其次,将无人机基站部署建模为局部互利博弈模型,并证明该博弈是精确势博弈,至少具有一个纳什均衡点;再次,在此基础上,提出了一种超启发式灰狼算法,通过迭代来逼近无人机基站最大覆盖要求下的纳什均衡点,实现最少无人机基站数量的最优部署;最后,仿真结果表明,所提出的解决方案在最小化无人机基站数量和加快收敛速度方面具有显著的优势。
