地下采煤情况下地表黄土边坡稳定性分析

马宗源,焦 贝,党发宁,成玉祥

(1.贵州交通职业技术学院,贵州 贵阳 551400;2.西安理工大学岩土工程研究所,陕西 西安 710048;3.长安大学地质工程与测绘学院,陕西 西安 710054)

0 引言

我国是煤炭开采量较大的国家,许多地区由于煤层埋深较浅,地下采煤诱发地表变形并造成严重塌陷。近年来，由于地下煤层开采诱发的黄土边坡破坏及滑坡失稳情况日趋严重,严重影响了煤矿生产安全及当地民众的生活。1991年8月,陕西铜川金华山煤矿西侧黄土梁边由于采煤引起大规模的崩塌性黄土滑坡,土体达1 050万m3,滑坡体将坡脚处的西龙村埋没,摧毁大片农田。2004年4月4日1时20分,由于多个煤矿开挖导致陕西彬县城关镇下沟村发生3次大面积山体滑坡,滑坡体黄土涌入水帘小河,将河流截断,数百名群众紧急撤离。2005年甘肃华亭煤矿区砚峡村受采空区塌陷影响诱发了大型滑坡,体积达395万m3,致使砚峡村部分房屋出现裂缝及倒塌,学校、医院、信用社等公用设施遭到不同程度的破坏,直接经济损失达2 000多万元。2010年7月,陕西省延安市某矿区发生大规模黄土滑坡,滑坡体积达10万m3,滑坡及坡体变形如图1所示。从现场滑体特征可以看出,滑坡速度极快,滑体冲向对面斜坡,所幸未造成人员伤亡。2011年7月,吕梁市方山县山西焦煤集团霍州煤电有限责任公司方山店坪煤矿发生一起黄土滑坡,滑体掩埋多个建筑及设备,造成5名人员死亡。由此可见,地下采煤引发的滑坡灾害已经成为煤矿开采区除地面塌陷灾害外最严重的地质灾害形式[1]。根据张银洲等[2]的研究,地下采煤形成采空区,当开采煤层的采深介于30～100 m时,就会产生较为强烈的地表变形,从而诱发黄土边坡失稳。

图1 矿区采矿诱发黄土滑坡及开裂Fig.1 Loess landslide and cracking in slope triggered by underground coal mining

目前国内外对地下开采诱发的滑坡已经进行了大量研究,但缺乏地下采煤诱发边坡失稳的有效分析方法及评价标准。现有研究大多是基于静力学理论进行分析[3-9]，而地下采煤对地表边坡的影响是一个动态变化的过程,开采过程中对地表边坡的扰动作用属于动荷载范畴,因此需使用动力学的理论及方法对地下采煤诱发边坡失稳问题进行计算分析。

本文以陕西省延安市黄陵矿区某煤矿发生的典型黄土滑坡为研究对象,使用显式有限元大变形计算方法分析不同煤层开挖高度情况下,开采扰动对地表黄土边坡安全系数的动态影响,提出一种适应于地下采煤诱发黄土边坡失稳及渐进破坏过程的分析方法,以期为黄土地区地下采矿诱发的边坡及滑坡灾害防治工程提供一定的理论指导。

1 研究方法及理论

1.1 土动力学基本理论

动三轴试验数据说明Hardin-Drnevich骨干加载曲线模型(下文简称HD模型)更适于预测饱和黄土的动应力-应变关系[10],因此采用土动力学模型分析地下采煤过程中开挖扰动对黄土边坡的影响,选取HD模型预测土的动模量和阻尼比随动应变的衰减关系。HD模型中土的动剪切模量和阻尼比可写为动剪应变的函数[11-12]:

(1)

(2)

式中:Gmax为土体动剪切模量的最大值;Dmax为土体的最大阻尼比;γ为土体的动剪应变幅值;γref为参考剪应变，γref=τmax/Gmax,即土体所受最大剪应力与剪切模量最大值的比值,可换算为G/Gmax=0.5时动剪切模量对应的动剪应变幅值γ,γref越大,土的动剪切模量随动应变衰减越快,土的阻尼越大。

基于HD模型建立黄土的动应力-动应变本构模型,由式(1)可推导出剪应力与剪应变的关系:

(3)

动力情况下,土体处于加、卸载循环状态,卸载时剪应力可写为:

(4)

再加载时有:

(5)

式中:γc为加、卸循环荷载转换时刻土体的剪应变;τc为加、卸循环荷载转换时刻土体的剪应力,τc可写为:

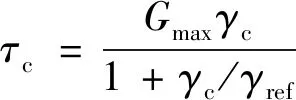
(6)

图2为不同土的动剪切模量、阻尼比与动剪应变的关系以及HD模型计算结果对比,其中砂土和黏土数据取自文献[13]和文献[14],陕北黄土数据取自文献[15]。采用Visual Fortran语言编制黄土动本构关系计算程序,并使用VUMAT子程序接口将模型导入ABAQUS有限元计算软件。用四节点减缩积分单元计算剪应力及剪应变关系,并与黄土动三轴试验测试数据进行对比。对该单元的顶部约束水平自由度,单元底部水平方向上加载正弦加速度时程曲线,正弦时程函数如式(7)所示,峰值加速度为0.04g:

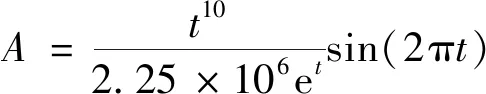
(7)

黄土动力学参数如下:剪切模量最大值Gmax=75 MPa,泊松比ν=0.25,参考剪应变γref=0.03。黄土的动应力与动应变关系理论预测与试验数据的对比如图3所示,可以看出根据HD模型建立的黄土动力本构模型能够很好地模拟黄土加卸载过程中呈滞回曲线形状的应力-应变关系。

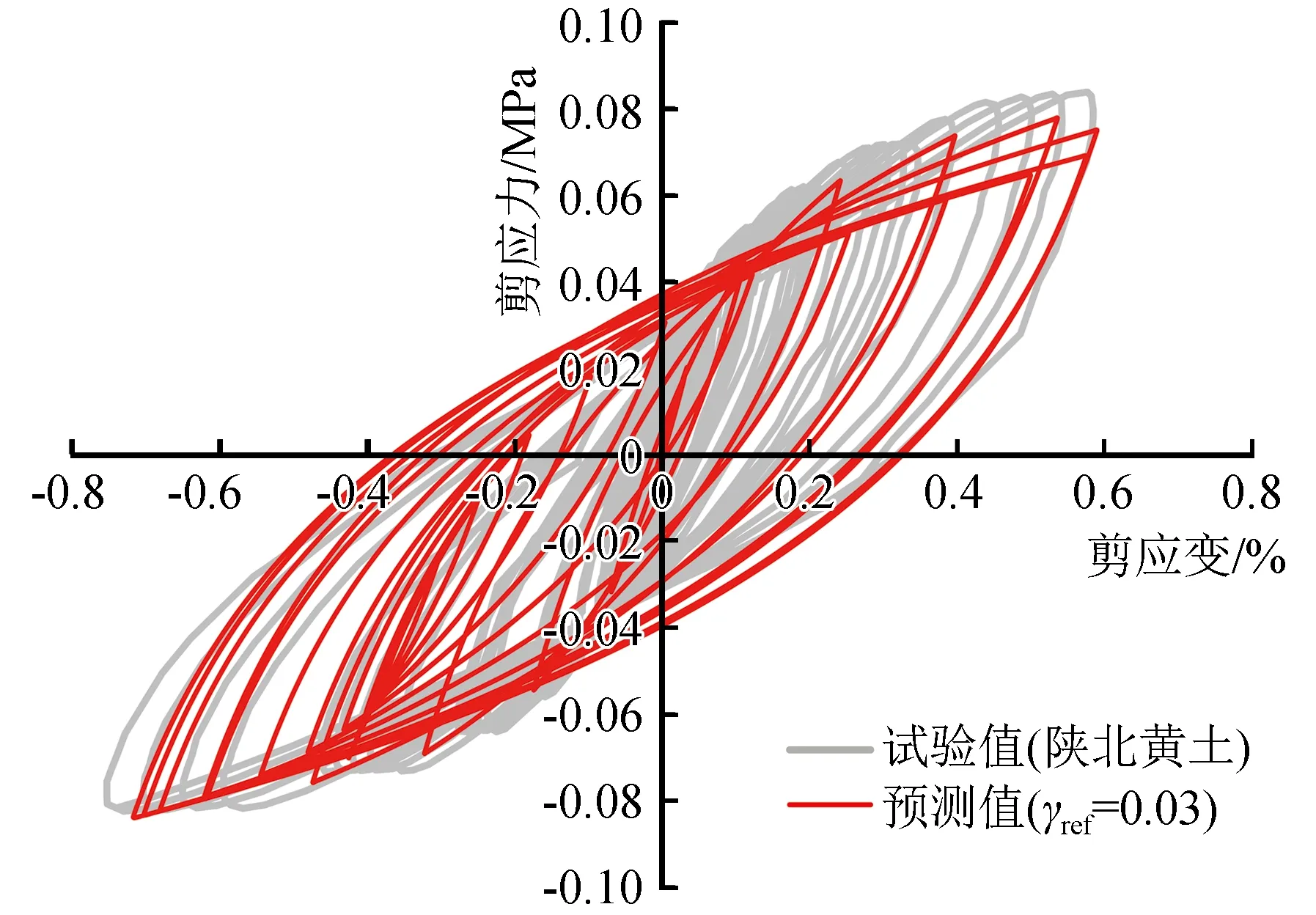
图3 黄土动应力与动应变关系理论预测与试验 数据的对比Fig.3 Comparison between theoretical prediction and experimental data of the relationship between dynamic stress and dynamic strain of loess

1.2 强度折减法计算边坡安全系数

使用强度折减法计算边坡的安全系数FOS(Factor of Safety)。边坡抗剪强度参数(黏聚力及内摩擦角)折减方式可写为[16]:

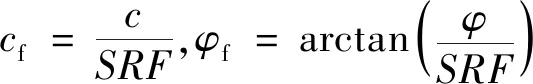
(8)

式中:SRF(Strength Reduction Factor)为折减系数;c和φ分别为边坡土体原始的黏聚力及内摩擦角;cf和φf分别为经过折减之后的边坡土体的黏聚力及内摩擦角。将边坡位移突然增大时刻(折减系数与边坡最大位移关系曲线拐点)的折减系数作为边坡安全系数。

以文献[16]中无下卧地层边坡算例作为对比,分别使用显式及隐式有限元方法计算边坡的安全系数,其中显式有限元方法采用大变形,隐式有限元方法采用小变形模式进行计算。算例边坡坡高10 m,坡比为1∶2。土体计算参数为:弹性模量E=100 MPa,泊松比υ=0.25,密度γ=2 000 kg/m3,黏聚力为c=10 kPa,内摩擦角φ=20°,不考虑剪胀角的影响,重力加速度g=9.81 m/s2。图4为本文使用显式有限元方法及文献[16]使用隐式有限元方法通过强度折减计算出的边坡最大位移结果的对比。由图4可以看出去,使用显式有限元和隐式有限元方法都可以通过强度折减系数与边坡最大位移关系曲线的突变确定边坡安全系数,但由于显式有限元方法采用大变形模式,因此边坡位移比隐式方法要大。图5为显式及隐式有限元方法得出的网格变形图,可看出二者差别不大。显式有限元方法采用显式时间积分方案求解动力学方程,材料及几何非线性问题不需要进行迭代,因此更适用于动力学及大变形问题的计算分析[17-18]。

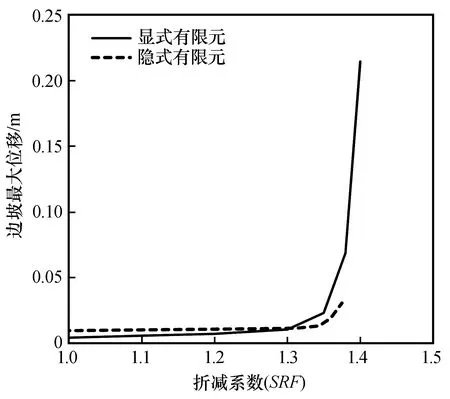
图4 通过强度折减计算出的边坡最大位移Fig.4 Maximum displacement of slope using the strength reduction method

图5 显式及隐式方法计算得出的边坡极限状态时的网格变形图(变形放大15倍)Fig.5 Mesh deformation of slope in limit state calculated by explicit and implicit methods (Scale factor is 15)

2 数值模拟研究

2.1 计算模型及边界条件

将实际问题简化为二维平面应变下均质土边坡问题,使用ABAQUS有限元软件的显式动力分析模块及大变形模式进行分析研究。根据实际工程概况,建立黄土边坡下煤层开挖模型,模型中黄土边坡的坡比为1∶2,坡高为30 m,计算模型尺寸及网格剖分情况如图6所示。其中,H为煤层开挖顶板埋深,h为煤层开挖高度,煤层向边坡方向开挖。使用二维四边形减缩积分单元进行网格划分,共划分14 076个单元,28 658个节点。由于将采煤扰动过程视为动力学问题进行计算分析,模型边界条件采用动力边界条件进行设置，将模型底部及两侧边界设置为零加速度边界,以保证计算域内产生的加速度、速度及位移以波的形式传播至边界处时不会反射回计算域内。但该边界条件会导致边界节点的位移及速度变化也为零,所以要尽量远离计算分析区域设置,以免影响位移及应力分布。煤层开挖顶板埋深H为100 m,开挖速度为10 m/天,在煤层开挖高度h为2.5 m、5 m、7.5 m的情况下分别计算边坡的稳定性。计算分析中黄土边坡土体强度准则使用Mohr-Coulomb准则,黄土体物理力学参数列于表1。

表1 计算参数汇总表Table 1 Summary of calculation parameters

图6 地下采煤边坡计算模型尺寸及网格 划分示意图(单位：m)Fig.6 Dimension and meshing of the slope model with underground mining (Unit:m)

2.2 计算结果及分析

图7、图8及图9分别为不同煤层开挖高度情况下,采煤过程中边坡及地层的位移云图。从采煤过程中边坡及地层的位移及边坡安全系数变化可以发现,边坡安全系数随开挖面与边坡坡脚距离L的减少而逐渐降低(负值代表挖过边坡坡脚的距离),同时边坡位移逐渐增大,边坡稳定性逐渐降低。

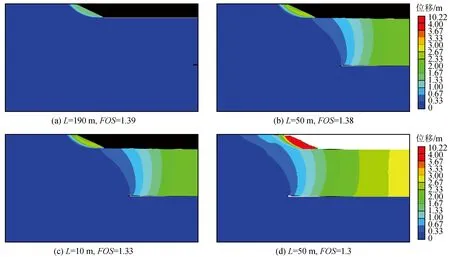
图7 不同开采位置边坡及地层的位移云图及安全系数(h=2.5 m)Fig.7 Displacement contours of slope and FOS with different mining positions (h=2.5 m)

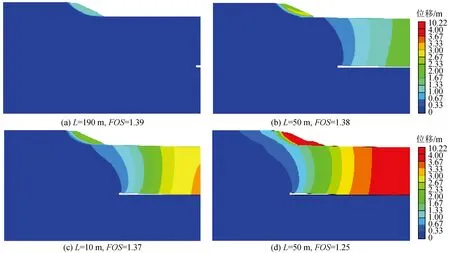
图8 不同开采位置时边坡的位移云图及安全系数(h=5 m)Fig.8 Displacement contours of slope and FOS with different mining positions (h=5 m)

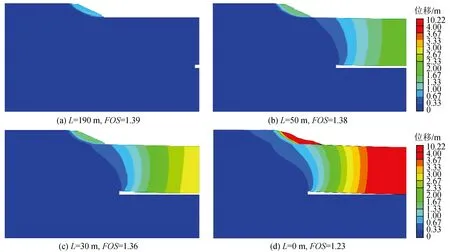
图9 不同开采位置时边坡的位移云图及安全系数(h=7.5 m)Fig.9 Displacement contours of slope and FOS with different mining positions (h=7.5 m)

图10为折减系数SRF=1.33时,地下采煤开挖过程中边坡坡顶水平向位移的变化情况,可以看出边坡位移随着开挖进尺的增加逐渐增大,在接近坡脚正下方时边坡坡体滑动破坏。图11为不同煤层开挖高度下边坡安全系数变化曲线,可以看出开挖前边坡处于静力情况下的安全系数(FOS=1.41),随着采煤开挖进尺的不断加大,边坡安全系数逐渐降低。此外,还可以看出地下采煤过程中边坡安全系数是动态变化的,因此地下采煤诱发边坡失稳也是一个渐进破坏的过程。不同煤层开挖高度下的计算结果(图11)显示,边坡安全系数变化的拐点相似,都是与坡脚水平距离40 m处,而煤层开挖高度7.5 m情况下边坡安全系数数值降幅明显,说明煤层开挖高度超过5 m将对地表边坡稳定性产生显著影响。

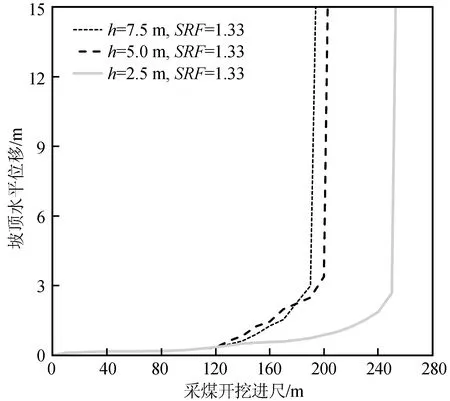
图10 地下采煤过程中边坡坡顶水平向位移变化Fig.10 Horizontal displacement variation of slope crest during underground coal mining

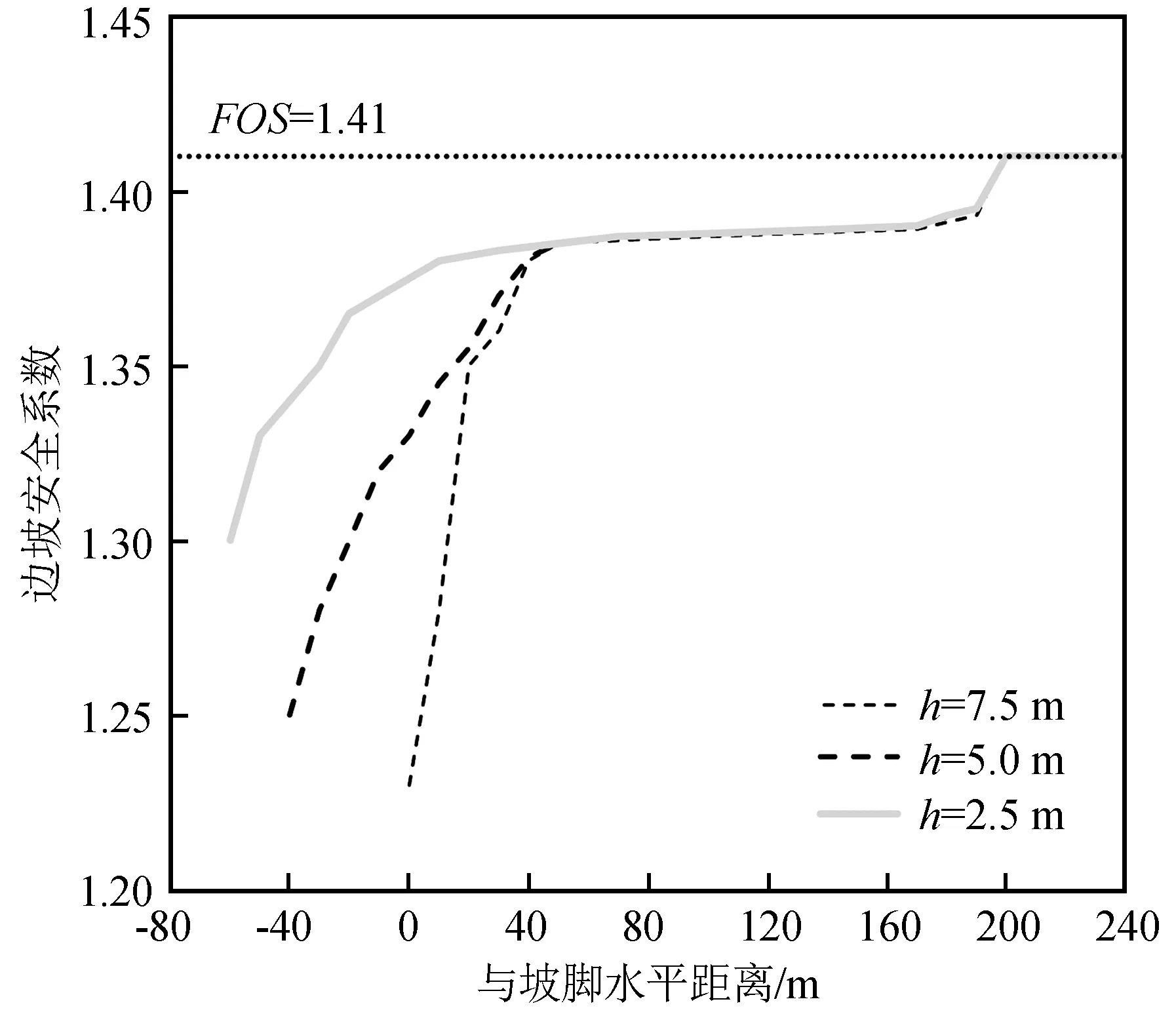
图11 地下采煤过程中边坡安全系数变化Fig.11 Variation of slope SOF during underground mining

3 结论

本文采用显式有限元及大变形计算方法分析了地下采煤对地表黄土边坡的稳定性影响问题,首先使用黄土动三轴试验结果对黄土动力本构模型进行验证,再对显式和隐式有限元计算方法进行对比分析,最后对地下采煤情况下地表边坡稳定性问题进行计算分析，并得出如下主要结论:

(1) 本文探讨了一种新的边坡稳定性分析方法,用来分析地下采煤等动态扰动情况下地表边坡的稳定性,该方法计算效率高且能够分析边坡的渐进破坏过程。

(2) 通过本文分析研究可知,地下采煤对地表边坡稳定性的影响是一个动态的过程,地表边坡失稳也是一个渐进破坏的过程,因此必须使用动力学方法及土动力学理论分析该类型边坡的稳定性问题。

(3) 在本文研究成果的基础上,下一步将考虑三维、煤层顶板塌落及地表裂缝等因素的影响,开展进一步研究。