基于MFCC样本熵和灰狼算法优化支持向量机的天然地震与人工爆破自动识别

庞 聪,江 勇,廖成旺,吴 涛,丁 炜

(1.中国地震局地震研究所,湖北 武汉 430071;2.地震预警湖北省重点实验室,湖北 武汉 430071;3.湖北省地震局,湖北 武汉 430071)

0 引言

天然地震与振动幅值较大的人工地震动事件具有许多相似的特性,区分研究它们的事件对地震目录生成、地震预警算法改进、强震动仪器抗干扰等至关重要。支持向量机方法被广泛应用于天然地震与人工爆破、塌陷等非天然地震动事件的分类识别研究中,取得了良好的研究成果与行业应用。如陈润航等[1]利用SVM识别186个首都圈天然地震事件和174个人工爆破事件;范晓易等[2]以MATLAB Lib-SVM工具箱为基础,进行天然地震、爆破及塌陷事件的多分类研究;黄汉明等[3]从天然地震和人工爆破事件信号中提取小波能量熵,应用支持向量机识别上述事件。支持向量机[1-3]在处理非线性问题上具有天然的优势,其分类机理在于选取一个核函数(线性核函数Linear、多项式核函数Poly、径向基核函数RBF以及神经元非线性作用核函数Sigmoid等)将低维样本数据映射到高维空间,构建并寻求一个最优分类超平面,但是其分类性能受核函数参数影响较大,采取算法优化的方式寻求一个合适的核函数参数值是当下SVM算法改进的主要方向之一。

对于事件性质辨识而言,特征判据与分类模型皆是影响识别效果的关键因素,寻找良好分类性能的判据也是众多研究人员不断尝试突破的工作方向之一。梅尔频率倒谱系数是一种应用于语音识别领域的数据处理方法,在近些年已被国内外相关人员应用到地震数据处理[4-5]中,更在2018年被陈润航等[6]应用至地震事件识别中,取得了良好分类效果,但是其直接利用梅尔频率倒谱系数(Mel Frequency Cepstral Coefficent，MFCC)各系数值组成的40维系数向量作为输入样本,训练过程较为复杂,存在较多的冗余或多重共线性特征参数,直接影响学习器的分类效果,限制了该特征判据的推广与应用。

本文基于灰狼算法优化SVM中的径向基核函数参数值,并从样本数据中提取梅尔频率倒谱系数、一阶差分系数及二阶差分系数的样本熵作为机器学习样本数据,并利用2013年四川芦山7.0级地震和人工爆破事件波形记录验证GWO-SVM分类器和MFCC样本熵特征的辨识效果。

1 基于灰狼算法改进的支持向量机

1.1 灰狼算法

灰狼算法[7](Grey Wolf Optimization Algorithm,GWO)是一种模拟狼群狩猎活动的新型群体仿生优化算法,在2014年由Mirjalili首次提出,它模仿狼群的四层等级制度,由头狼α、次级狼β、三级狼δ及普通狼ω等构成,狼群狩猎活动步骤主要分为追踪目标、围捕猎物及捕捉等,狩猎过程中的指挥命令优先级为:α>β>δ>ω。GWO算法具体步骤为:

首先狼群发现并确定目标位置,对目标进行包围,二者的距离表示为:

D=|C×Xp(t)-X(t)|

(1)

第t+1次迭代后灰狼的位置为:

X(t+1)=Xp(t)-A×D

(2)

式中:X(t+1)为第t+1次迭代后灰狼的最新位置坐标;A、C皆为系数调节因子;Xp(t)为猎物位置向量。

各个等级的灰狼实施围捕计划时,狼会带领狼对猎物实施追捕,追捕动作直接影响狼和猎物的位置变化。该过程的位置更新策略为:

(3)

(4)

Xp(t+1)=(X1+X2+X3)/3

(5)

式中:Dα、Dβ、Dδ分别表示α、β、δ狼与狼群中其他狼的距离;Xp(t+1)表示最接近猎物的灰狼位置,即最优解。

追捕到何时阶段,狼群开始攻击、捕捉猎物(最优解)。攻击速度的快慢通过调节参数a来完成,且A的取值范围为[-a,a],满足迭代停止条件后即得到最优解。

1.2 GWO优化的SVM识别算法

在处理非线性问题时,基于径向基核函数的支持向量机(SVM)分类效果很大程度上取决于参数惩罚系数c和核函数半径σ的赋值,通过引入灰狼算法优化上述两个参数,得到最优解,从而改进SVM分类机(优化流程如图1所示)。

图1 GWO-SVM辨识流程Fig.1 Identification process of GWO-SVM

(1) 通过某特征提取方法提取出若干个特征向量,建立特征数据集,同时按照一定比例划分训练集和测试集;

(2) 初始化狼群数目N、最大迭代次数t、目标猎物位置自变量数等参数;

(3) 遍历灰狼种群,计算每个个体的适应度fi:

fi=m/n

(6)

式中:m为被SVM分类器准确识别的样本数量;n为参与SVM分类的总样本量。将适应度值最大的三个灰狼位置分别记为Xα、Xβ、Xδ;

(4) 计算α、β、δ狼与狼群中其他狼的距离Dα、Dβ、Dδ,同时更新上述狼的位置,以及刷新参数a、A、C值;

(5) 循环计算(3)～(4),直至迭代次数达到迭代次数临界值t,并得到最佳目标位置,即最优解;

(6) 设置SVM参数,将得到的最优惩罚系数和最优核函数半径最优值替换RBF核函数中默认的初始参数值,以构建新的GWO-SVM分类器;

(7) 应用测试集与GWO-SVM模型进行地震属性辨识,得到天然地震与人工爆破的识别结果。

2 数据集与特征提取

2.1 数据集

选取2013年芦山7.0级地震事件的360条强震动记录和39条人工爆破记录,其中芦山地震震中位于30.3°N、103.0°E,震源深度13 km;爆破事件位于中国水利水电科学研究院岩土所试验场,信号采样率为1 000 Hz,采用1.58倍TNT当量的RDX球型炸药。原始记录统一截取长度为12 000的数据,并进行数据归一化、NaN去除等数据预处理操作,消除台站所处环境、仪器精度、波形幅值等因素可能给数据分析带来的不利影响。图2(a)为天然地震事件震动波形图;图2(b)为不同人工爆破事件的固定分量信号。

图2 天然地震与人工爆破信号Fig.2 Signals of natural earthquakes and artificial blasting

2.2 梅尔频率倒谱系数

梅尔频率倒谱系数[8](MFCC)是语音识别领域中被广泛应用的特征提取算法。步骤为:

(1) 预加重:采用数字滤波器补偿初始信号中受抑制的高频信号,该滤波器的传递函数为：

H(z)=1-μz-1

(7)

(2) 加窗:窗函数一般采用汉明窗,使得相邻两窗口之间有重叠区域,即

0≤n≤N-1

(8)

(3) 时频域转换:对各窗口信号进行离散傅里叶变换(DFT),将信号从时域变换到频域,其计算公式为:

(9)

(4) 计算Mel滤波器组对数能量:将每个窗口的频谱取模的平方得到功率谱,并除以该窗口采样长度,然后经Mel滤波器组滤波,得到第m个梅尔滤波器组输出能量的对数,即得到对数能量s(m)。

(10)

式中:Hm(k)为第m个三角滤波系数。

(5) 得到MFCC各阶系数:对数能量s(m)经离散余弦变换(DCT)后,即可得到第n阶梅尔频率倒谱系数

(11)

经过上式计算,只能得到MFCC静态L阶系数,包含原始信号的静态特性,而研究信号的动态特性就需要单独提取动态系数(一阶差分系数和二阶差分系数等),即

(12)

式中:dt为第t个一阶差分;Ct即第t个倒谱系数;Q为倒谱系数Ct的阶数;K是一阶导数时差值。

以天然地震和爆破事件中随机各取出一条记录为例,得到的MFCC静态系数、MFCC一阶差分系数、MFCC二阶差分系数,其中Mel滤波器的阶数设置为24,离散余弦变换系数维度为12,信号长度为8 000,预加重滤波器参数取为0.937 5,窗函数采用汉明窗。由于MFCC一阶差分系数及其二阶差分系数的首尾两帧皆为0,这里作删除处理。同时,由于MFCC系数的幅值与维数一般呈现显著的负相关性,维数越低,系数的幅值越大,为降低地震事件类型辨识所需的特征向量维数与特征矩阵复杂度,提高辨识效率,可只提取MFCC静态系数矩阵、MFCC一阶差分系数矩阵及MFCC二阶差分系数矩阵的第一维系数,具体如图3所示。

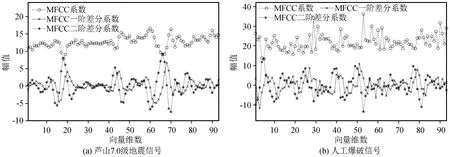
图3 天然地震与爆破信号的MFCC系数首维特征提取结果Fig.3 The first-dimensional extraction results of MFCC from signals of natural earthquakes and blasting

2.3 提取MFCC各阶系数样本熵

通过MFCC分析法,将得到的MFCC静态系数向量组、MFCC一阶差分系数向量组及MFCC二阶差分系数向量组的首维系数向量分别记为{M1(i),i=1,2,…,N}、{M′1(i),i=1,2,…,N}及{M″1(i),i=1,2,…,N},其中N为MFCC每一维系数向量的长度。

样本熵[9](Sample Entropy,简称SampEn)是一种可表征一维离散样本内部混乱状态的特征值,由学者Richman等于2000年提出。由于天然地震事件与人工爆破事件的震源机制、传播波形、瞬时最大能量、能量衰减规律等皆有明显差异,将样本熵应用至MFCC各系数向量的状态特征描述中是一种新的尝试。样本熵计算步骤为:

(13)

(14)

(15)

(3) 将维数增加至m+1,重复步骤(1)～(2),得到Bm+1(r)

(16)

(4) 样本熵的计算公式为

(17)

在实际应用中,嵌入维数m常取2,阈值r为原始样本的标准差×自定义权值,其中权值常取0.15或0.2。

3 实验与分析

本实验硬件条件为:Intel(R) Core(TM) i5-8400 @ 2.80GHz,内存为8 G的Windows10 64位操作系统,实验平台为MATLAB 2019a。采用国家地震科学数据共享中心(data.earthquake.cn)提供的2013年芦山7.0级地震事件的360条强震动三分量记录(EW、NS、UD),及中国水利水电科学研究院岩土工程研究所(www.geoeng.iwhr.com)与陈祖煜院士团队提供的39条人工爆破事件数据,共399条加速度幅值记录,并根据本文特征提取方法从长度一致的归一化三分量数据中得到一个399×3的MFCC系数样本熵特征矩阵(图4),其特征从分别为MFCC静态系数首维向量样本熵、MFCC一阶差分系数首维向量以及样本熵MFCC二阶差分系数首维向量样本熵。

图4 MFCC系数样本熵特征提取结果Fig.4 Feature extraction results for MFCC coefficient sample entropy

由图4,人工爆破信号(样本号:361～399)与天然地震信号(样本号:1～360)存在较大的区分度,爆破信号波形特征较为一致,样本熵变化幅度较小,天然地震信号成分较复杂,不同信号波形特征差异较大,其MFCC系数样本熵值变化明显。MFCC静态系数首维向量样本熵(记作Mfcc0_SE)、MFCC一阶差分系数首维向量样本熵(记作Mfcc1_SE)以及MFCC二阶差分系数首维向量样本熵(记作Mfcc2_SE)的t检验结果如表1所列,显著性水平设置为0.05,3个特征参数的假设检验结果均为1,符合特征参数有明显地震事件区分能力的预期目标。

表1 天然地震与爆破信号的单一特征向量t检验结果Table 1 The t-test results of single eigenvector of signals of natural earthquakes and blasting

实验方案设计为:特征矩阵按360∶39比例随机分成训练集Tr360×3与测试集Te39×3,对应的标签值向量为训练集标签列向量Lr360×1与测试集标签列向量Le39×1,共含2个辨识子实验,其循环次数分别为100次和1 000次,实验结果如图5和表2。

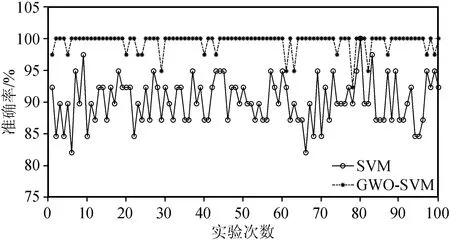
图5 GWO-SVM与SVM模型辨识结果对比Fig.5 Comparison between identification results of GWO-SVM and SVM models

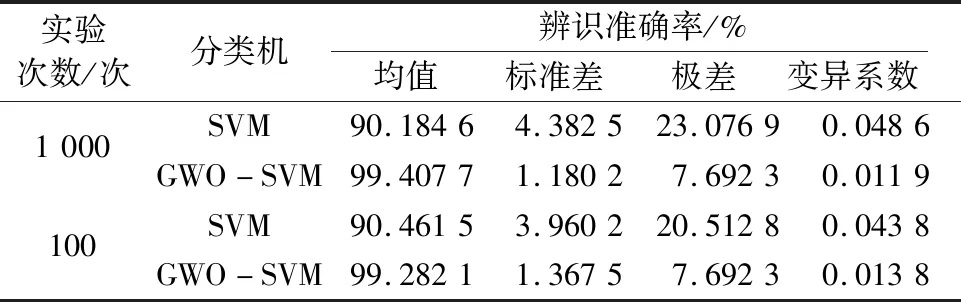
表2 1 000次循环辨识实验结果Table 2 Identification results of experiment under 1 000 cycles

由图5和表2可看出,GWO-SVM分类机的辨识性能各方面都优于SVM分类机,不论是小型实验和较大型实验,GWO-SVM算法都保持了较为稳定的辨识效果:以1 000次循环辨识实验为例,GWO-SVM的识别准确率稳健性指标—标准差、极差、变异系数分别为1.180 2、7.692 3、0.011 9,均远低于SVM的4.382 5、23.076 9、0.048 6;在100次辨识实验条件下,GWO-SVM的辨识曲线与SVM曲线边界区分明显,大部分的连续点位连线体现为水平分布趋势。这证明:GWO-SVM算法具有更强的非线性目标求解能力与稳健性,实现了灰狼算法优化支持向量机关键参数惩罚系数c与核函数半径σ的预定辨识目标。优化参数列于表3。

表3 GWO-SVM辨识结果中的c与σ(部分)Table 3 c and σ in GWO-SVM identification results

表3数据来自1 000次循环辨识实验结果中随机抽取的12份惩罚系数与核函数半径优化结果,由于每一个辨识过程所需的样本数据都是随机组合的,这导致灰狼算法优化得到的惩罚系数最优值与核函数半径最优值也相差较大,但这丝毫不影响GWO-SVM分类机的辨识性能。优化后的SVM分类器辨识性能得到明显的提升,识别结果基本稳定在95%以上,证明支持向量机中惩罚系数与核函数半径的最优值选取与训练集数据息息相关,也验证了本文辨识方案的有效性和可行性。

为了验证GWO-SVM在地震事件类型识别中的优越性,在同样的训练集与测试集基础上,本实验采用RobustBoost集成学习、LDA、PLDA等3种机器学习分类模型与GWO-SVM模型进行辨识效果对比实验,4个模型的辨识次数与识别效果如图6所示。

图6 4个辨识模型的识别率图Fig.6 Identification rates of four models

由图6可知,GWO-SVM模型除了明显改善SVM分类机识别性能,还在同类型的机器学习方法中有一定优势,具有较突出的曲线平稳特性。

4 结论

本文引用灰狼优化算法优化传统支持向量机,并采用MFCC三维系数样本熵作为特征样本,提出一种新型地震事件性质辨识方法。核心要点在于使用灰狼算法优化支持向量机径向基核函数(RBF)中的惩罚系数和核函数半径,使之最大程度地匹配训练集和支持向量机模型,形成新的GWO-SVM分类器,然后对测试集进行辨识实验。辨识结果表明:

(1) GWO-SVM模型性能明显优于SVM分类器,也优于RobustBoost、LDA、PLDA等学习机,灰狼算法的参数优化效果高度匹配预期目标;

(2) MFCC静态系数、MFCC一阶差分系数、MFCC二阶差分系数样本熵作为地震事件类型辨识判据,积极拓展了天然地震与人工爆破辨识研究在机器学习判据上的空白。

本文研究可作为一种探索性方法应用到中小型地震预警系统或地震学研究中,以进行天然地震与其他非天然地震事件的分类识别,从而降低地震事件误判概率。但是在实际监测中,天然地震事件性质识别除了会受到人工爆破事件的干扰外,也存在监测仪器受到电磁干扰后生成异常波形、塌陷地震等各种干扰事件类型。并且,学习样本数量和数据种类如果较少,只能说明在当前实验数据下是积极可行的,缺乏普适性实验论证。鉴于以上只是新方法的初步探讨,下一步将重点收集各类相关数据,研判该方法在不同震级、不同震中区域、多种地震动事件下的辨识差异性与有效性,挖掘更多有现实意义的地震事件类型辨识方法。

致谢:感谢中国地震局工程力学研究所和中国水利水电科学研究院岩土工程研究所提供数据支撑。