面向口腔软接触的蔗糖溶液润滑特性研究

丁宗如， 钱善华,2,*， 王 亮， 周帅帅， 卞 达

(1.江南大学 机械工程学院， 江苏 无锡 214122；2.江苏省食品先进制造装备技术重点实验室， 江苏 无锡 214122)

生物摩擦学是摩擦学研究极其活跃的领域之一[1]，其中涉及舌、上颚、牙齿、食物等相对运动的内容被定义为口腔摩擦学[2]。近年来，摩擦学已被广泛应用于食品领域，主要包括食品感官属性[3-5]及食品安全[6]等的评定。

鉴于伦理和技术的限制，真实口腔环境中的摩擦行为难以测量，体外模拟口腔摩擦是目前口腔摩擦学研究的主要方法[7]。研究人员在口腔组织的仿生材料制备及性能表征[8-9]、唾液[10-11]和部分流体食品的摩擦性能[12-14]等方面开展了一些研究，如：聚二甲基硅氧烷(polydimethylsiloxane，PDMS)是模拟口腔软组织的较好材料[9]，洋槐蜜和大米糖浆之间较大的润滑性能差异有助于检测蜂蜜中是否掺假[14]等。能够直接应用到口腔摩擦学中的摩擦性能测试的仪器设备较少，相比于机械零件之间的摩擦，口腔摩擦学相关的研究并不常见，且体外模拟口腔摩擦试验需要考虑多个维度的影响[2]，集中在试验上的研究难以衡量多重因素的复杂影响；食物的口腔加工过程复杂而特殊，虽然被划分边界润滑、混合润滑和流体动压润滑等润滑区域[15-16]，但试验测定结果和理论推导的润滑区域未能有效衔接。

含蔗糖的饮品是一种常见饮品，在饮品中添加蔗糖可以增加饮品甜度并改善口感[17]，但其热量较高，过量摄入容易增加疾病风险[18-20]，而无糖或低糖饮品又因为蔗糖的缺失往往在口感上和常规含糖饮品有一定的差异，如可乐等饮料中蔗糖被甜味剂替代后，即使表观甜度水平相同，感知的口感也会发生显著变化[21]，兼具口感与健康的饮品有着极大的市场需求[22-24]。通过感官评定试验发现蔗糖能够降低抗氧化提取物溶液[25]和柠檬/酸橙饮料[21]的涩味，而涩感通常被认为是一种与口腔润滑行为密切相关的触觉感知[2]，因此蔗糖缺失导致的口感差异可能和蔗糖溶液润滑性能存在一定联系。同时，随着口腔摩擦学的发展，饮品的顺滑感已被证实与口腔润滑行为密切相关，较低的摩擦系数通常意味着较好的顺滑感[15,26-27]。对于饮品企业而言，兼具口感和健康的无糖或低糖饮品以及具备良好顺滑感的含糖饮品的设计需要对含糖饮品的润滑特性有一个更深的认识。目前，含糖溶液的润滑特性方面的研究报道较少，闫凌等[28]通过调整配方使特定无糖饮料的润滑性能接近常规饮料从而改善口感，是含糖饮品润滑特性少数的研究之一，但其未能提供饮料润滑特性的影响因素。对不同蔗糖质量分数的含糖饮品而言，亟需深入研究不同配比蔗糖溶液的润滑特性来为“减糖不减味”的低糖或无糖替代品以及具备低摩擦特性的高顺滑感新品的研发提供更好的技术支持。

本研究将构建口腔软接触的模拟环境，配制不同蔗糖浓度的含糖溶液，开展其润滑特性的研究，并建立软接触的滑移模型，将数值结果与试验结果对比，希望揭示含糖饮品的低摩擦特性的影响因素，为口腔环境下流体食品润滑状态的判别和饮品的研发提供技术参考。

1 材料与方法

1.1 材料与试剂

PDMS(Sylgard 184)，美国道康宁公司；蔗糖，上海泰坦科技股份有限公司；无水乙醇，国药集团化学试剂有限公司。试验所用试剂均为分析纯。

1.2 仪器与设备

DZF- 6050型真空干燥箱，上海一恒科学仪器有限公司；DHR- 2型旋转流变仪，美国TA公司；MFP- D型白光干涉仪，美国Rtec公司；MFT- 5000型摩擦试验机，美国Rtec公司。

1.3 试验方法

1.3.1PDMS摩擦副制备

通过不锈钢的球模具和塑料的盘模具制备口腔仿生软材料——软球和软盘。在20g的PDMS基本组分中加入2 g固化剂，搅拌后超声波振荡3 min保证固化剂分散均匀并消除部分气泡，放入真空干燥箱中负压静置消除剩余气泡，待气泡完全消除后倒入模具。将模具水平静置于70 ℃的烤箱，5 h后取出，自然冷却12 h制得所需PDMS球和盘。PDMS球的直径为9.5 mm，PDMS盘的直径为50 mm，厚度为3 mm。使用前需在PDMS盘的中心钻出直径2 mm的孔位，同时为避免PDMS球和盘表面在制备和加工过程中可能存在的污渍对试验结果造成影响，将PDMS球和盘放入无水乙醇中进行8 min的超声清洗后再用去离子水冲洗，最后在真空干燥箱内干燥。制备球和盘的PDMS基本组分和固化剂质量配比均为10∶1[29]，其材料的弹性模量和泊松比分别为2.21 MPa和0.31，弹性模量和泊松比委托北京中科光析化工技术研究所测得。

1.3.2蔗糖溶液配制

根据程韵静等[30]的研究，一般市售的瓶装饮料和手打奶茶的含糖量在10%(质量分数)左右。查阅中华医学百科全书[31]，发现单糖浆的蔗糖质量分数为64.7%，因此配制6组不同质量分数的蔗糖溶液(10%、20%、30%、40%、50%、60%)开展试验，即将蔗糖与去离子水混合，均匀搅拌后配制6组不同质量分数的蔗糖溶液。制备后的蔗糖溶液将立即使用，防止蔗糖溶液中水分蒸发析出蔗糖晶体而影响其测试结果。

1.3.3PDMS摩擦副微观形貌测试

采用白光干涉仪观测PDMS球和PDMS盘的表面形貌，并使用配套软件(gwyddion)计算其表面粗糙度。

1.3.4蔗糖溶液流变和润滑性能测试

目前，食品的流变学测试主要集中在测量有限剪切速率下的黏度和食品的表观屈服应力，以及有限的一组频率上的存储/损耗模量，作为黏弹性的量度[26]。蔗糖溶液属于黏性流体，只需测量其在有限剪切速率下的黏度。采用旋转流变仪开展不同质量分数蔗糖溶液黏度随剪切速率的变化测试。试验中，采用上压头为锥板(直径为40 mm，锥度为2°)，测试平台示意图见图1。图1中的测试平台的上压头和下平台之间充满蔗糖溶液，下平台固定、上压头旋转。根据测定上压头和下平台相对旋转时使蔗糖溶液受剪切的阻力矩，计算蔗糖溶液的动力黏度，相关测试参数：测试温度为25 ℃、剪切率区域为1～1 000 s-1、流体高度(h)为200 μm，每组蔗糖溶液重复测量3次。

图1 流变仪测试平台Fig.1 Test platform of rheometer

基于PDMS球对PDMS盘的软接触摩擦副，在摩擦试验机上开展不同质量分数蔗糖溶液的润滑性能测试，润滑性能测试装置示意图见图2。图2中的PDMS球通过螺纹夹具固定在金属销上，金属销与传感器相连；PDMS盘固定在液池底部，与旋转装置相连，固定于机座；蔗糖溶液倒入液池并浸没PDMS盘。试验时，PDMS球与PDMS盘在外载荷作用下接触，其中PDMS球保持静置，PDMS盘匀速旋转，致使摩擦副产生相对滑动，通过力传感器测量其滑动过程中摩擦系数。根据不同质量分数蔗糖溶液的平均摩擦系数与工况参数的关系以表征其润滑性能，工况参数选取参考业内认可的参数[11-12]。该试验在常温(25 ℃)下进行，载荷为3 N，滑动速度从1 257.10 mm/s降低至1.57 mm/s，试验时间为60 s，每组试验均需要更换新的PDMS球和PDMS盘。

图2 润滑性能测试装置Fig.2 Lubrication performance test device

1.4 口腔软接触滑移模型建立与求解

1.4.1口腔软接触滑移模型建立

当PDMS球和PDMS盘接触时，将两个接触体等效成一个当量弹性球体和一个刚性平面来考虑弹性变形，其当量弹性模量E计算方法见式(1)。

(1)

式(1)中，E1和E2分别为球和盘的弹性模量，MPa；ν1和ν2分别为球和盘的泊松比。根据1.3.1中测得的弹性模量和泊松比，则E为2.44 MPa。在本试验中，采用同类软材料模拟口腔软接触时，接触载荷和滑移速度相对较低，运动摩擦时所产生的热量较小，故不考虑其温度的变化；流体食物的分子间隙小，在研究其宏观运动时忽略分子间的孔隙，将流体食物视为连续介质流体。采用等温点接触的Reynolds方程和含弹性变形的膜厚方程建立口腔软接触的滑移模型。该模型借鉴了Vicente等[32]的软接触模型，采用黄平[33]的量纲归一化方法，在膜厚方程中增加了粗糙度函数。为了保证模型求解的完整性，选择Roelands黏压方程表征其黏压特性。滑移模型的基本方程包括：Reynolds方程、膜厚方程、黏压方程和密压方程。量纲归一化后的Reynolds方程见式(2)。

(2)

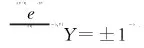
(3)

式(3)中，X0和Xe是求解域x方向的量纲归一化起始坐标。量纲归一化后的膜厚方程见式(4)。

(4)

式(4)中，Y0和Ye是求解域y方向的量纲归一化起始坐标；H0为量纲归一化的中心点膜厚；S和T为对应于X和Y的附加坐标。量纲归一化后的黏压方程见式(5)。

η*=exp {(lnη0+9.67)[-1+(1+5.1×10-
9P·pH)0.68]} 。

(5)

量纲归一化后的密压方程见式(6)。

(6)

摩擦副表面粗糙对其计算结果有一定的影响，而真实表面的轮廓较复杂，故须要对其表面开展适当的简化处理。本研究将采用正弦曲面代替实测表面[34]，其曲面函数见式(7)。

δ(x)=Acos (2πx/wx) 。

(7)

式(7)中，δ(x)为表面粗糙度函数；A为表面粗糙度幅值；wx表示在x方向的波长，mm，wx取0.06 a。表面粗糙度幅值根据表面粗糙度均方根选取。量纲归一化后的粗糙度表面函数方程见式(8)。

r(x)=Bcos (2πx/0.06) 。

(8)

式(8)中，B是量纲归一化后粗糙度值幅，B=ARx/a2。此外，摩擦力F是通过对润滑区域的剪切应力τ积分获得，摩擦力的计算公式见式(9)。

(9)

式(9)中，τ是剪切应力，Pa。在流体润滑区域，当润滑油流动时会形成剪切应力，采用Vicente剪切应力模型[33]计算此区域的剪切应力，剪切应力计算方程见式(10)。

(10)

式(10)中，正负号分别对应上下表面承担的剪切应力，第一项是Couette项，第二项是和压力梯度有关的Poiseuille项。将摩擦力与接触区的液体承受载荷W相比，即可获取其摩擦系数f。

图3 PDMS球和PDMS盘表面形貌Fig.3 Surface morphology of PDMS spheres and PDMS discs

1.4.2口腔软接触滑移模型的求解过程

滑移模型相关方程主要为偏微分方程，影响方程的是变量相对变化量而非变量本身的值，故采用量纲归一化(又称无量纲化)的方法简化方程组。简化后的量纲归一化方程采用有限差分法迭代求解，获得接触区的压力和膜厚，根据Vicente剪切应力模型计算接触区域的剪切应力，得到摩擦系数。在方程组迭代时，以Hertz接触压力为初始压力分布，采用多重网格法求解其光滑解，以此作为粗糙解初值直接迭代，获取其粗糙解。无量纲求解区域为-1.5≤X≤2.5，-2≤Y≤2，网格最高层129×129个节点，最底层17×17个节点，迭代过程中使用载荷平衡方程控制压力和油膜厚度的迭代；在最高层，对于离散后的原方程进行迭代，其他层都是对于原方程的缺陷方程进行迭代，且只在最底层调整其膜厚。迭代收敛的判断准则为压力的相对收敛准则，即要求前后两次迭代得到的压力差小于0.001。为确保计算结果的正确性，运算结束前校验其载荷误差，数值计算程序采用Fortran语言编写。

值得强调的是，在点接触模型中，两个表面的粗糙度被合并到一个表面，另一表面被视为光滑表面，不考虑两个表面粗糙峰的相互作用。若假设摩擦副表面光滑，则使用多重网格法直接获得特定工况下光滑解；如果考虑真实表面的微观形貌对膜厚方程的影响，则求得粗糙解；即便粗糙度函数已经简化，求得的粗糙解精度仍会降低，且更易于发散。为解决该问题，本研究将从光滑解出发，逐渐增加粗糙度幅值，将以前粗糙度稍小的解作为下次求解的初值进行求解。

2 结果与分析

2.1 PDMS球和PDMS盘的微观形貌分析

图3为PDMS球(a)和PDMS盘(b)的表面形貌。由图3可知，PDMS球的表面相对粗糙，有明显的沟壑和凹坑，其表面粗糙度均方根Rq为1.82 μm。PDMS盘的表面相对光滑，表面粗糙度均方根Rq为14.8 nm。PDMS球和PDMS盘的粗糙度差异主要来源于制备模具，PDMS球使用不锈钢模具，PDMS盘使用塑料模具，塑料模具表面比金属模具表面更为光滑。将实测的表面形貌应用于滑移模型中，鉴于PDMS盘比较光滑，不考虑其粗糙度的影响，两表面的粗糙度不做整合，直接采用PDMS球粗糙度数据构建其表面粗糙度函数。

2.2 不同质量分数蔗糖溶液黏度随剪切速率的变化

图4为6组蔗糖溶液黏度(η)与剪切速率(γ)的变化关系。由图4可见，蔗糖质量分数对溶液黏度有较大影响；随着剪切速率的增加，质量分数10%～40%的蔗糖溶液黏度基本不变；在剪切速率为10 s-1～100 s-1时，质量分数50%的蔗糖溶液黏度呈线性缓慢增加，质量分数60%的蔗糖溶液黏度呈线性下降，当剪切速率超过100 s-1，二者黏度基本保持不变；剪切速率在100 s-1之后，6组蔗糖溶液的黏度维持稳定，认为其黏度不再随剪切速率变化，即便剪切速率超过1 000 s-1，溶液黏度仍能维持稳定；6组溶液近似为牛顿流体，且随着蔗糖质量分数的增加，溶液黏度也随之升高。对于软接触摩擦副，即便是很低的滑动速度都对应着较高的剪切速率[35]，因此选取剪切速率在1 000 s-1附近的稳定值作为不同质量分数蔗糖溶液的黏度，则10%～60%质量分数的蔗糖溶液的黏度分别为0.001 2、0.002 0、0.004 4、0.008 0、0.048 0、0.100 0 Pa·s。

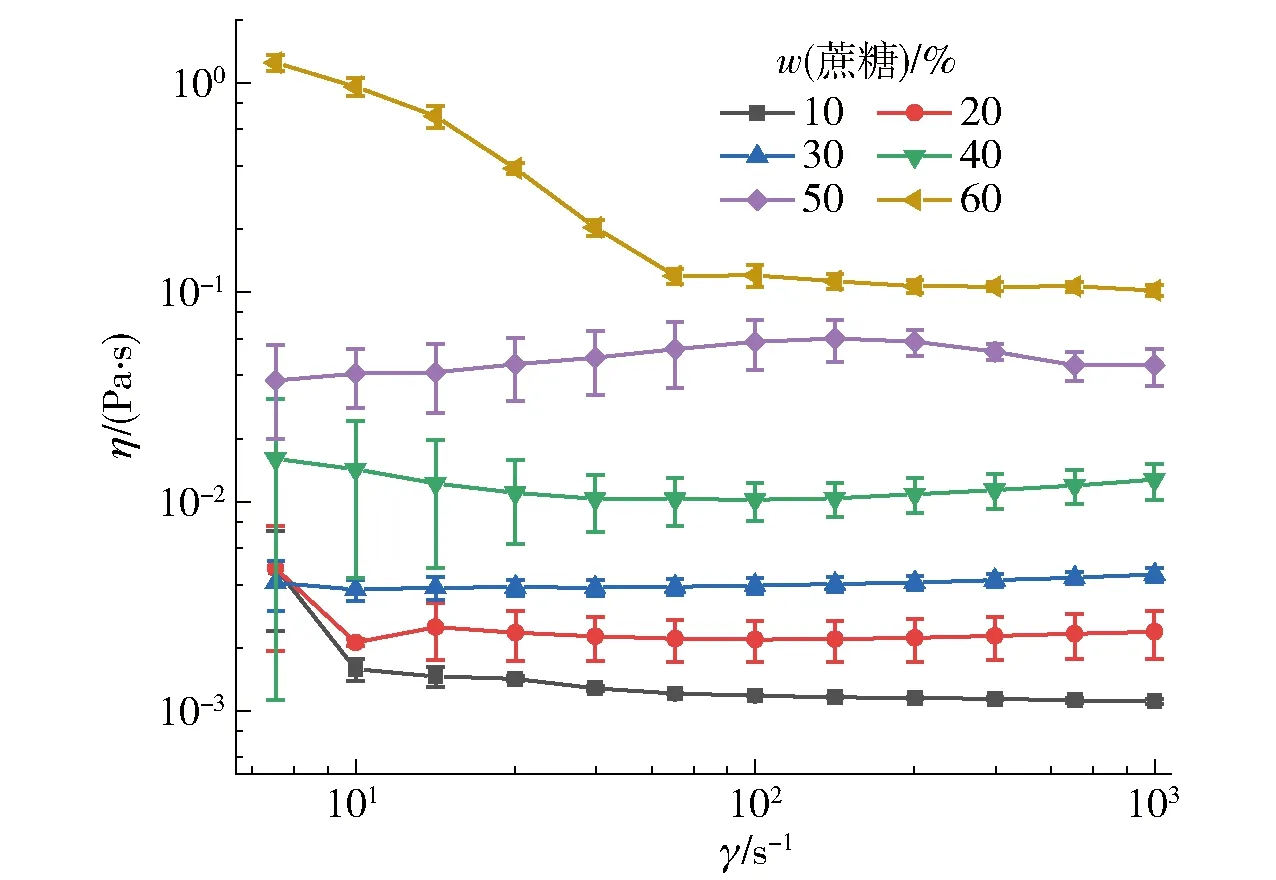
图4 蔗糖溶液黏度与剪切速率的关系Fig.4 Relationship of viscosity with shear rate of sucrose solutions

2.3 不同质量分数蔗糖溶液润滑性能的分析

图5为不同质量分数蔗糖溶液的平均摩擦系数随滑移速度和速黏积(滑移速度×黏度，uη)的变化关系。由图5(a)可见，在整个滑移区间内，质量分数10%和20%的蔗糖溶液的平均摩擦系数先基本不变后减小，润滑区域主要处于边界润滑和混合润滑区域；质量分数30%和40%的蔗糖溶液经历完整的润滑区域(边界润滑、混合润滑和流体润滑区域)；质量分数50%和60%的蔗糖溶液润滑区域主要处于混合润滑和流体润滑区域。质量分数10%～40%的蔗糖溶液在滑移速度较低时，没有或只有微量液体被卷吸到摩擦副的接触区，故仅观察到边界润滑或者混合润滑状态，但其在边界润滑区域的摩擦系数较为接近，表明蔗糖的质量分数对其边界润滑性能产生微乎其微的影响；在质量分数50%和60%的蔗糖溶液中，即便滑移速度较低，仍能观察到流体润滑状态。

图5 不同黏度流体平均摩擦系数与滑移速度和速黏积的变化关系Fig.5 Variation in average coefficient of friction with slip velocity and product of slip velocity and viscosity of 6 sucrose solutions

由图5(b)可见，蔗糖溶液的平均摩擦系数在相同速黏积下虽有波动但大体重合；随着uη增大，平均摩擦系数呈现先基本不变后减小再增加的变化趋势，属于Stribeck曲线的典型特征；边界润滑和混合润滑的拐点在uη=7×10-5Pa·m附近，混合润滑和流体润滑的拐点在uη=4×10-3Pa·m附近。在uη<7×10-5Pa·m时，软摩擦副处于边界润滑状态，摩擦副表面发生了真实的接触，平均摩擦系数较高；当uη为7×10-5～4×10-3Pa·m时，软摩擦副处于混合润滑状态，随着uη的增大，其平均摩擦系数逐渐减小；在uη>4×10-3Pa·m时，软摩擦副处于流体润滑状态，摩擦副表面的微凸体将不再接触，此时摩擦副的表面摩擦力不受表面性质影响，只与流体的黏度和滑移速度有关，增加速度或黏度均会增加黏性阻力，从而导致其平均摩擦系数的升高。由2.2中结果可知，随着蔗糖溶液中蔗糖质量分数的增加，溶液的黏度也逐渐升高，由图5中不同质量分数蔗糖溶液平均摩擦系数随u和uη的变化可知，在边界润滑区域，即使蔗糖溶液的质量分数不同，同一滑移速度下的平均摩擦系数也基本相同；在混合润滑区域下，蔗糖质量分数较高的溶液，其黏度较高，同一滑移速度下，uη也较大，其平均摩擦系数反而较小；在流体润滑区域，uη的增加会导致平均摩擦系数上升，因此质量分数较高的蔗糖溶液在同等工况下平均摩擦系数也较高。不同质量分数的蔗糖溶液在模拟口腔软接触摩擦副中的润滑性能存在差异，润滑性能又与顺滑感密切相关[15,26-27]。 Ares等[25]通过感官评定试验还发现蔗糖能够降低抗氧化提取物溶液的涩味，而涩味是一种与口腔润滑相关的触感，因此蔗糖的缺失导致的口感差异可能和蔗糖溶液润滑性能存在一定联系。

图6 不同表面沿X轴方向的压力和膜厚分布Fig.6 Pressure and film thickness distribution of different surfaces along X axis

虽然本次试验只选用了6种流体，但研究结果不限于这6种流体。在真实进食过程中，更低的摩擦系数，意味着更好的顺滑感和更舒适的吞咽感[15,26-27]。流体润滑状态的判定有助于揭示其低摩擦系数的影响因素。在图5(b)中，不同质量分数蔗糖溶液的平均摩擦系数在相同uη下有较好的重叠，这种现象能够运用于新型同类流体食品的研发。只要确定这些流体食品的黏度，初步预测其在不同滑移速度下摩擦系数，从而判别其润滑状态，能够为顺滑感的新型食品研发提供较好的技术支撑。在混合润滑和流体润滑的交界处附近，即当uη在0.001～0.010 Pa·m区域内，蔗糖溶液有着较低的摩擦系数。考虑不同人群的需求[36]，根据他们的吞咽速度，能够为其选择合适黏度的饮品，使饮品在口腔状态下的uη更接近于混合润滑向流体润滑转变的拐点，从而获得较好的顺滑感和吞咽的舒适性。

2.4 口腔软接触滑移模型分析与验证

根据1.3.4中试验参数设置口腔软接触润滑模型的相关参数，即球和盘的当量弹性模量为2.44 MPa，载荷为3 N，球半径为9.56 mm，且球在盘表面为纯滑动。当假设软球和软盘表面均光滑[δ(x)=0]，即不考虑摩擦副表面粗糙度的影响，从而获得光滑解；若考虑粗糙表面的影响，根据2.1中试验结果，取粗糙度幅值为2.6 μm(表面粗糙度均方根Rq为1.82 μm)，构建粗糙度函数，从而获得其粗糙解。当uη=7×10-2Pa·m时，光滑表面和粗糙表面工况下量纲归一化后的压力和膜厚沿X轴方向(速度方向)接触中心的分布见图6。摩擦副接触区域的压力在接触中心的当量半径范围内有显著变化。在光滑表面工况下，压力和膜厚在整个坐标轴上过渡较为平滑；在粗糙表面工况下，压力在接触中心附近有较为明显的锯齿状波动，但膜厚的变化在光滑表面下差别较小。区别于经典弹流条件，在压力分布图中未发现第二压力峰。流体在摩擦副之间的压力和膜厚分布是流体润滑理论研究的重要内容，压力控制着摩擦副的变形，膜厚则影响着润滑状态的转变，流体的压力和膜厚分布一定程度上代表着其润滑性能[2,37]，利用口腔软接触滑移模型提供蔗糖溶液在不同表面的压力和膜厚分布，将为其润滑机理的探究提供理论帮助。

模拟口腔需要考虑多个维度的影响，包括材料的弹性模量、粗糙度、亲水性、疏水性和摩擦副的运动方式等。鉴于多个维度的影响和试验条件的限制，真实口腔环境下摩擦测试是食品摩擦学的难点。从理论研究的角度出发，建立合理的数值模型研究能够较好地弥补试验研究的局限。在与1.3.4同等参数条件下，考虑粗糙度的影响(粗糙度幅值为2.6 μm)，在μη为0.01～0.20 Pa·m选取了一些不同的uη进行了计算，与图5(b)对比，分析结果见图7。由图7可见，随着uη的增加，流体的平均摩擦系数呈现逐渐增加的趋势(0.01～0.20 Pa·m)，符合流体润滑区域摩擦系数的变化特性；数值计算结果和对应的试验结果差别较小，证实了口腔软接触滑移模型的有效性，也验证了部分试验结果，说明试验和模型的有机结合帮助了流体食品润滑状态的判别。在本研究建立的口腔软接触的润滑模型中，采用确定性的粗糙表面，提供了牛顿流体在流体润滑区域中压力和膜厚的真实信息，加之其在流体动力润滑区域的数值结果和试验结果的一致性，表明该模型具有较好的潜在应用价值。

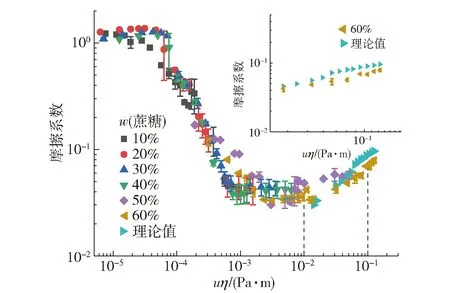
图7 数值计算结果与试验数据对比Fig.7 Comparison between numerical and experimental data

3 结 论

本研究表明，6组质量分数不同的蔗糖溶液近似为牛顿流体，黏度基本上不随剪切速率而变化，且随着蔗糖质量分数的增加，溶液黏度也逐渐升高；在PDMS软球和软盘构建的口腔软接触摩擦副中，蔗糖溶液的润滑性能与速黏积(uη)高度相关，随着uη的增加，蔗糖溶液的摩擦系数经历了先稳定后减小再增加的变化过程，表明其润滑状态从边界润滑向混合润滑过渡，最后转移到流体润滑区域；当uη处于0.001～0.010 Pa·m时，蔗糖溶液的润滑状态在混合润滑和流体润滑状态的交界附近，摩擦系数较低；口腔软接触滑移模型能够提供光滑和粗糙表面条件下蔗糖溶液在流体润滑状态下的压力和膜厚分布以及摩擦系数，并验证同等工况参数下部分试验结果的有效性。