直驱风机机网侧变流器统一建模及其弱电网下稳定性研究
2022-10-11汪春江孙建军宫金武查晓明
汪春江,孙建军,宫金武,查晓明
(武汉大学 电气及自动化学院,武汉 430072)
0 引 言
可再生能源发电并网是缓解能源危机,降耗去霾的有效途径[1],风电作为可再生能源发电的一种主要形式,近年来在国内得到快速发展,电网中风电占比不断攀升。然而,风速固有的随机性、波动性、间歇性等特性,势必对电力系统的安全稳定运行带来不可忽略的影响,尤其是并入弱电网时影响尤为恶劣。国内外已出现多起这类稳定性问题,振荡频率跨越10 Hz-1 000 Hz[2-5]。这种由风电变流器控制引起的振荡频率和衰减率由控制参数和交流电网参数决定,且比次同步谐振发散得更快,应引起足够的重视[6-7]。因而,研究弱电网下风电的稳定性问题势在必行[8]。
针对弱电网下风电并网的稳定性问题,目前国内外在这方面已经有一部分研究进展。由于风电变流器普遍采用的背靠背拓扑形式,使得机侧和网侧变流器动态在一定程度上解耦,在研究变流器控制的稳定性时常常将机侧和网侧变流器其一进行简化。文献[9]研究了影响双馈风机轴系振荡的因素,考虑轴系、发电机及机侧变流器控制动态,认为机侧控制参数和控制策略的不当会引发不稳定现象;文献[10]则研究了直驱风机发生次同步振荡的机理,将风力机、永磁同步发电机和机侧变流器及其控制系统简化建模为受控电流源模型,认为风机台数的增多和电网强度的变弱引发系统阻尼变弱导致不稳定;以上研究都忽略了网侧控制的动态,将其等效为恒压源。文献[11-12]研究弱电网下直驱风机的稳定性问题,认为网侧变流器的控制参数与控制策略对稳定性有关键性影响,而锁相环控制涉及到与电网电压的同步,也对稳定性至关重要。以上研究都忽略了机侧控制的动态,将其等效为恒功率源。
以上研究并没有同时考虑机侧及网侧控制,从系统多时间尺度控制的角度,机侧与网侧控制的时间尺度是存在重叠的[13],即同一时间尺度内,同时存在机侧和网侧变流器控制的影响。因此,需要同时考虑机侧及网侧变流器控制动态的影响。
传统的变流器并网稳定性分析方法主要有状态方程法[11]和阻抗法[14]。阻抗法目前多用于网侧变流器并网稳定性分析中,在这类分析中,机侧变流器动态被忽略,因此无法利用阻抗法分析考虑机网侧变流器控制的并网稳定性。
综上,文章针对弱电网下直驱风机的稳定性问题,首先建立含直驱风机机网侧变流器控制的统一模型;在此基础上,提出了包含机网侧变流器控制的稳定性分析方法,对比传统的阻抗分析方法,并进行了相应的实例分析;最后通过simulink仿真对分析的结论进行了验证。
1 直驱风机变流器控制
1.1 机侧变流器控制
文章研究的直驱风机机网侧变流器控制框图如图1所示。
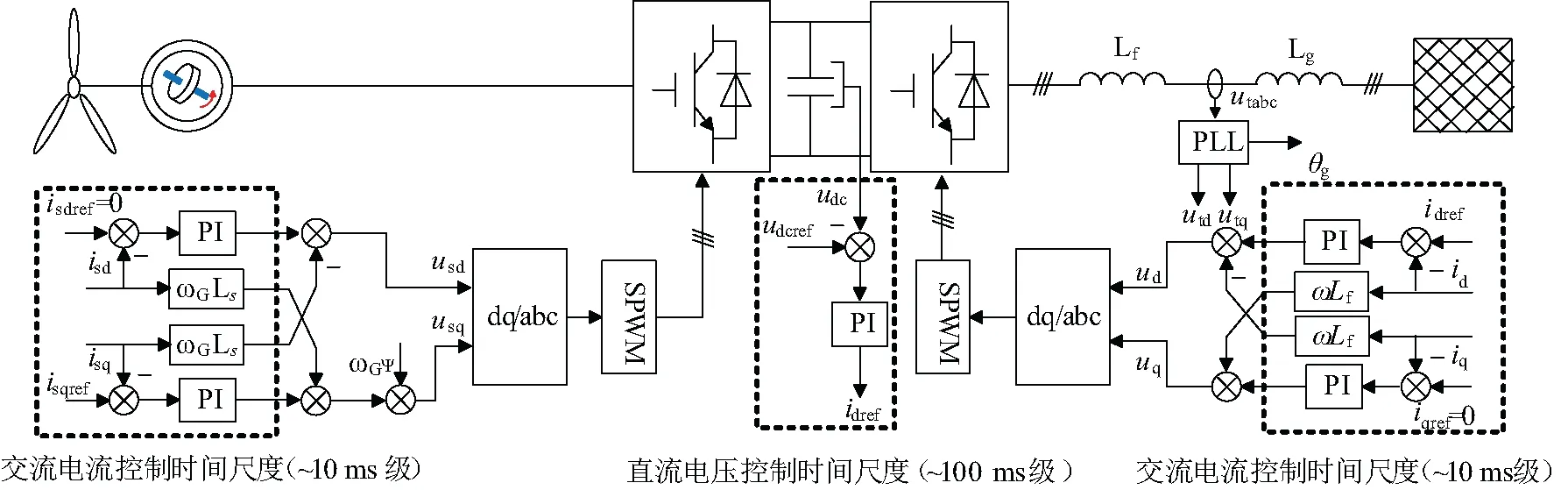
图1 直驱风机机网侧变流器控制框图
如图1所示,机网侧控制分两个时间尺度,直流电压控制时间尺度与交流电流控制时间尺度,在交流电流控制时间尺度内,机网侧实际存在耦合的。因此,考虑含交流电流时间尺度动态时,机网侧动态应同时考虑。
机侧采取转子磁场定向的矢量控制,d轴定位于转子永磁体的磁链方向上。该永磁同步发电机的电压方程及转矩方程为:
(1)
式中Rs、Ls分别为发电机的定子电阻、电感;us、is分别为定子电压电流;下标d、q代表d轴、q轴分量;ωG为发电机转速;Ψ为转子永磁体磁链;p为电机极对数。发电机转矩直接由定子电流q轴分量控制。
控制器外环控制转速,内环控制定子d、q轴电流,均采用PI控制,控制关系如下:
(2)
式中kp、ki分别为PI控制的比例及积分系数;下标ref为该项变量的指令值。
1.2 网侧变流器控制
如图1所示,网侧变流器控制采取电网电压定向的矢量控制。其电压方程为:
(3)
式中Lf为滤波电感;u、i分别为变流器输出电压电流;ut为滤波后电压;ω为电网侧电压角速度;下标0代表稳态值。
控制器外环控制直流侧电压,内环控制电网d、q轴电流,均采用PI控制,控制关系如下:
(4)
1.3 弱电网特性
考虑弱电网情形,即电网存在较大的阻抗(用电网电感模拟),其电压方程为:
(5)
式中Lg为电网电感;ug为电网电压。
2 小信号模型
2.1 机侧变流器控制建模
对式(1)、式(2)进行小信号化处理,认为转速不变,有:
(6)
(7)
联解上述公式:
(8)
在变流器并网的稳定性分析中,常常将机侧变流器等效为一个恒功率源,即ΔPG=0,这样实际上是忽略了机侧变流器的控制动态对稳定性的影响,而考虑到如上的机侧变流器控制动态,机侧变流器的输出功率为:
ΔPG=ωG0ΔTG=T1(s)·Δisqref
(9)
其中:
2.2 网侧变流器控制建模
对式(3)~式(5)进行小信号化处理,有:
(10)
(11)
(12)
对于网侧变流器,其交流侧输出功率如下:
(13)
小信号化:
(14)
联解上述公式,有:
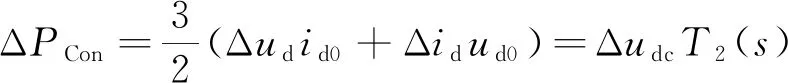
(15)
其中:
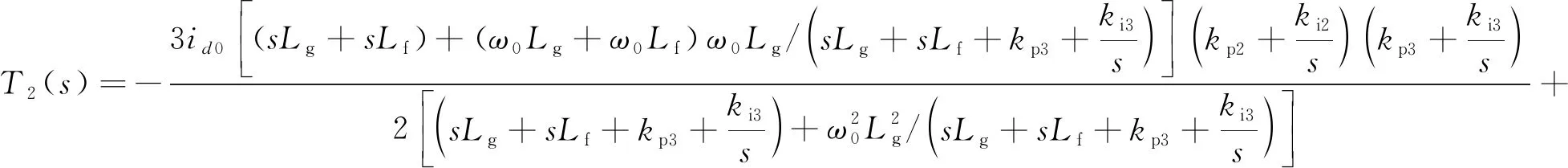
(16)
3 稳定性分析
3.1 阻抗分析方法
使用阻抗分析法,则忽略机侧变流器控制动态,机侧变流器输出功率认为是恒功率,即ΔPG=0。并网系统可以化为如图2所示等效电路。
Zi、Zo分别为电网阻抗矩阵,变流器输出阻抗矩阵,Δis、Δug、ΔuPCC、Δi分别为变流器受扰动后空载电流变化量、交流电网受扰动后空载电压变化量、并网点电压受扰动后变化量、并网电流受扰动后变化量。由叠加原理,该系统满足关系式:

图2 并网系统等效电路
ΔuPCC=[E+YoZi]-1(Δug-ZiΔis)
(17)
文中所有加粗量均为矩阵或向量,E为单位矩阵,Yo为矩阵Zo的逆。对于图2所示的三相逆变器并网系统,(E+YoZi)-1是一个2维矩阵,记为矩阵G:
(18)
式(17)可以写作:
(19)
式中y为输出;u为输入:
y=ΔuPCC,u=Δug-ZiΔis
(20)
在实际系统中,由于逆变器和电网在独立运行时一般是稳定的,即u是稳定的,因此并网系统的稳定性由G的零极点分布决定。对于2输入2输出系统,闭环系统稳定等效为Gdd、Gdq、Gqd、Gqq均没有右半平面的极点,文中以分析Gdd为例。变流器输出阻抗如下,依据为式(10)~式(11):
(21)
交流电网的输入阻抗如下,依据为式(12):
(22)
3.2 统一建模稳定性分析方法
系统的动态特性反应到电气量上是交直流电压电流的变化,而不稳定是输入输出功率不平衡的表现。分析系统的交直流侧瞬时功率关系如下。
有小信号关系式:
(23)
结合之前建立的小信号模型,可以得到如图3、图4所示的稳定性模型。
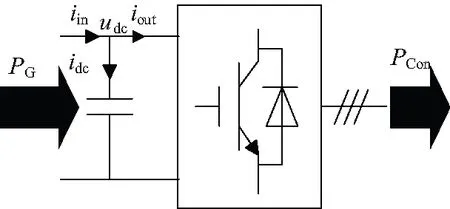
图3 交直流侧瞬时功率平衡关系
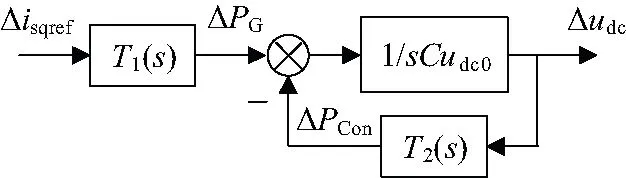
图4 稳定性分析模型
如上述模型所示,系统的稳定性用直流电压的稳定性来表征。Δisqref是风机定子电流指令值扰动量,该值由风机最大功率跟踪控制决定。即直驱风机并网系统的稳定性受控制参数、电网电感及最大功率跟踪控制动态影响。
3.3 实例分析
分析及仿真采用的直驱风机并网系统参数如表1所示。
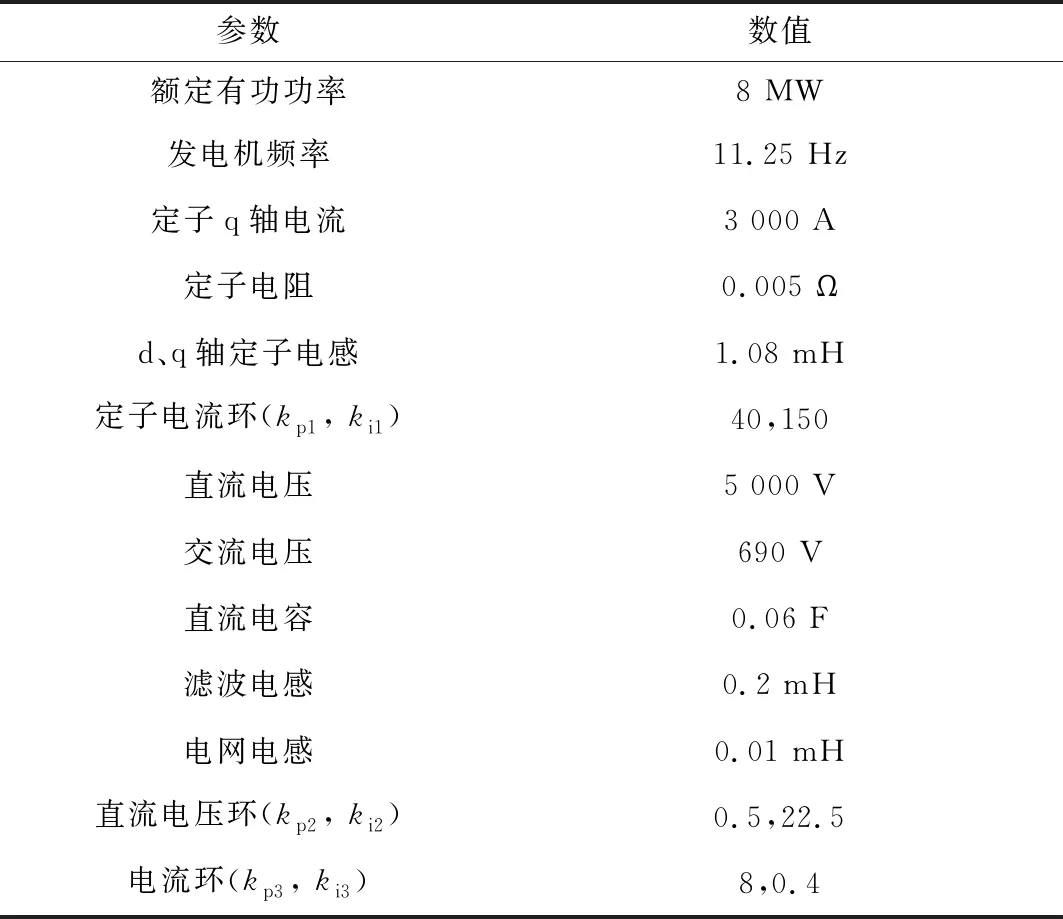
表1 直驱风机并网系统参数
根据上文所述的阻抗分析法及统一建模稳定性分析方法,得到闭环系统的极点分布如图5所示。 此时,系统稳定性分析存在两种结果,统一建模分析法的结果是系统仍旧稳定,而传统的阻抗分析法得到结果系统已经失稳,二者存在差异性。很明显,对于阻抗分析法而言,0.01 mH已经是分析得出的系统失稳时的电网电感边界。增大电网电感,利用统一建模分析继续计算极点。

图5 闭环极点分布对比图
对于文中采用的统一建模分析法而言,0.03 mH才是系统失稳时的电网电感边界。明显,阻抗分析法在分析电网电感边界时拥有更强的保守性,如图6所示。

图6 电网电感增大时闭环极点分布
4 仿真验证
依据表1的参数及图1的拓扑及控制框图,搭建Simulink仿真模型以验证上述分析。如图7所示为仿真得到的直流电压波形。
直驱风机在初始的并网动作之后,直流电压迅速回复到5 000 V的额定值,此时系统是稳定的,与统一建模分析法的结果相符。增大电网电感,探寻仿真情况下电网电感失稳边界,如图8所示。
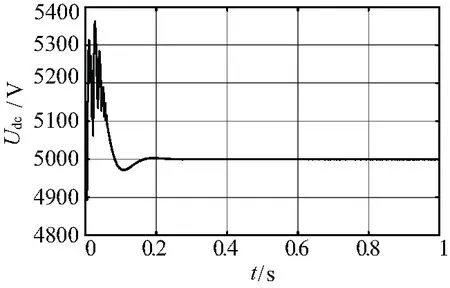
图7 仿真直流电压波形
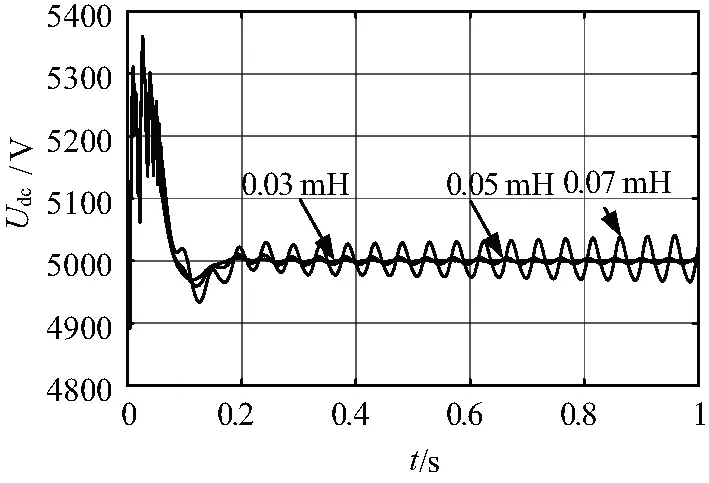
图8 电网电感增大时直流电压波形
陆续增大电网电感至0.07 mH,在初始的并网动作之后,直流电压没有回复至5 000 V,而是在5 000 V附近出现了20 Hz频率的增幅振荡,此时,系统开始失稳。比较阻抗分析法的0.01 mH与考虑机网侧变流器控制的统一建模分析法的0.03 mH,文中提出的分析方法具有更弱的保守性,对于预测直驱风机并入弱电网的电网电感边界有更高的精确性。
5 结束语
文中研究了弱电网下直驱风机并网的稳定性问题,建立了考虑机侧和网侧变流器控制耦合的统一分析模型,并给出了考虑机侧和网侧变流器控制的稳定性分析方法,并利用Simulink仿真对分析结果进行了验证,得到以下结论:
(1)直驱风机机网侧变流器控制之间存在时间尺度上的耦合,在分析并网稳定性时只考虑网侧将造成分析误差;
(2)直驱风机并网系统的稳定性不仅受机网侧控制参数及电网电感决定,还受最大功率跟踪控制动态影响;
(3)考虑机网侧变流器控制的统一建模分析方法,比较传统的阻抗分析法,具有更弱的保守性,对于预测直驱风机并入弱电网的电网电感边界有更高的精确性。
