基于GOOSE通信的地铁多变流器智能优化控制方法研究
2022-06-28杜贵府郑子璇
何 斌,杜贵府,郑子璇
(1. 中铁第四勘察设计院集团有限公司,武汉 430063;2. 苏州大学轨道交通学院,江苏苏州 215031)
采用全控型器件的双向变流器由于在稳定直流侧电压、提升系统安全性能等诸多方面具有优势,在国内外地铁牵引供电系统中有着广泛的应用前景[1]。然而,在双向变流器向列车供电以及向交流侧反馈再生制动能量的过程中,线路阻抗和装置特性难以避免地导致了网络损耗的产生,大大降低了系统的能量利用率[2]。此外,牵引电流自走行轨、回流线向变流器回流的过程中,走行轨纵向电阻的存在导致了钢轨电位的产生,同时由于走行轨对地绝缘不理想等原因,部分回流电流泄漏至周围土壤、管道,形成了杂散电流,造成周边设备的腐蚀,甚至威胁到乘客及工作人员的生命安全[3-5]。由于各变流器的工作特性对线路网络损耗、钢轨电位等有着较大的影响,如何实现地铁多变流器的优化控制成为目前研究的重点之一。
目前针对多变流装置控制策略的研究多集中于微网发电系统。经典的主从控制策略对主电源的依赖性强,且电流平衡控制器会对电压调节回路产生影响[6]。而对等控制策略能够调节并维持多变流器的输出电压,但无法有效应对系统故障或大扰动[7]。与主从控制模式、对等控制模式相比,分层控制模式能够实现全系统的协调控制,且模式简单、易于实现,因此在直流微网等多变流器并联系统中应用十分广泛[8-9]。然而,目前地铁牵引供电系统内的各变流器均以各牵引所处的单台设备为工作单元,独立实现其预设的功能,无法相互配合或根据系统级的实时需要进行快速调整。各变流器之间、各变流器与系统级之间缺乏信息交互,导致各设备无法实现阈值的动态调整,难以降低系统损耗或避免环流等。而GOOSE通信机制能够满足多变流器间快速报文的需求,实现数据的快速、可靠传输,具有较强的互操作性和实时性,适用于建立多变流器通信网络,从而实现多变流器协调控制[10]。
在多变流器协调控制研究中,如何在不同的系统运行状态及约束下,调整变流器参数从而寻找预定目标最优解并达到系统稳定状态是相关研究的重点之一。诸多学者将电力系统中类似的大规模非线性优化问题统称为最优潮流问题并深入研究[11-12]。传统的优化算法如梯度下降法、牛顿法等由于容易陷入局部最优解或存在奇异矩阵等缺点,逐渐被粒子群算法、模拟退火算法、遗传算法等智能优化算法所替代[13-15]。刘先正等[16]提出了一种基于模糊控制理论的自适应粒子群算法,从而在降低系统网损的同时保证了线路电压质量。黄俊辉等[17]基于模拟退火遗传算法进行了交直流系统的无功优化及电压控制,从而降低系统网损并降低无功经济成本。
因此,本文提出了一种基于GOOSE通信的地铁多变流器智能优化控制方法。首先,根据地铁直流牵引供电系统结构及双向变流器的工作特性,基于GOOSE通信机制建立了全线变流器通信网络。其次,基于 GOOSE通信网络建立了多变流器分层控制策略,并以系统网络损耗最小和钢轨电位最小为目标,提出了多变流器双目标优化控制算法作为全局优化算法。以NSGA-II算法为例求解该双目标优化控制算法的帕累托解集并选取最终解,并基于 MATLAB平台针对国内某实际线路进行潮流仿真。仿真结果表明,与无优化或无通信优化时相比,本文所提出的基于GOOSE通信的多变流器智能优化控制方法能够实时、准确地调节全线变流器的参数,从而降低系统能耗、提升系统安全性能。
1 系统介绍
如图1所示,在地铁牵引供电系统中,双向变流器将35 kV交流电整流为1 500 V直流电,并通过上行、下行接触网向处于牵引工况的列车提供牵引电流。同时,处于制动工况的列车通过双向变流器将再生制动能量反馈至交流侧。牵引电流普遍通过走行轨、回流线向变流器回流。此外,为抑制钢轨电位和杂散电流,地铁线路多安装有杂散电流收集网(stray current collection systems,SCCS)以及过电压保护等接地装置。然而,钢轨电位和杂散电流异常升高现象仍频繁发生。
为实现多变流器协调控制,本文建立了基于GOOSE通信机制的多变流器通信控制系统,如图1所示。假设全线共N个变流器,各变流器均通过GOOSE网络与控制器相连,同时N个变流器之间也可通过该网络实现快速通信。通过设置控制器的控制策略,可以实现不同功能的多变流器动态管理和实时控制,从而优化变流器性能、准确控制变流器的输出特性、提升系统效能及安全性。

图1 地铁牵引供电系统结构示意Figure 1 Structure of traction power supply system of subway
各变流器工作特性如图2所示,分为整流工况、退出工况、逆变工况 3个工作区。当牵引网电压Udc低于整流工况启动阈值Uz时,变流器进入整流工况,将35 kV交流电整流为1 500 kV直流电,此时牵引网电压Udc与牵引电流Idc的关系如式(1)所示。

图2 变流器工作特性Figure 2 Working characteristics of converter

其中,Rz为变流器在整流工况下的等效内阻,此时Idc>0。在各变流器输出特性的调节过程中,Uz、Rz均可调整,其调节范围可分别记为Uzmin~Uzmax、Rzmin~Rzmax,且Uzmin应不低于变流器空载电压。
当牵引网压Udc高于Uz但低于逆变工况启动阈值Un时,变流器处于退出工况,此时变流器无输出电流,Idc=0。当牵引网电压Udc高于Un时,变流器进入逆变工况,将制动列车产生的多余的再生制动能量反馈至交流网侧,此时Udc与Idc的关系如式(2)所示。

其中,Rn为变流器在逆变工况下的等效内阻,此时Idc<0。在各变流器输出特性的调节过程中,Un、Rn同样均可调整,其调节范围可分别记为Unmin~Unmax、Rnmin~Rnmax,且Unmax应不高于接触网最大允许电压。
2 多变流器分层控制策略
2.1 多变流器分层控制结构
基于GOOSE通信网络,本文提出如图3所示的多变流器分层控制策略。其中,各变流器的本地控制器为第1层控制。在多变流器并联系统中,为稳定电压幅值和系统频率,第1层控制多采用下垂控制。各本地控制器通过 GOOSE通信网络进行实时信息交互,并将各变流器电压、频率、功率等信息反馈至第2层控制的中央控制器。中央控制器设置有全局优化算法,根据该时刻全线各变流器的工作特性进行协调控制,并将控制信号通过GOOSE通信网络发送至各本地控制器,进行变流器控制信号的二次修正,从而实现降低全线网络损耗、提升系统安全性能等目标。其中,第2层控制所采用的全局优化算法可根据不同的优化目标及其数量,选取合适的智能优化算法来求解该优化问题,如采用非支配解排序遗传算法(NSGA-II)求解非线性规划问题等。图3所示的多变流器分层控制结构的模式简单、易于实现,且能够基于全线各变流器状态进行实时的、系统的调整,在系统性能优化方面具有较大的优势。

图3 多变流器分层控制策略Figure 3 Hierarchical control strategy of multi-converter
2.2 多变流器双目标优化控制算法
考虑到地铁线路运行工况复杂,能量损耗大且回流安全问题日益突出等因素,选取系统网络损耗最小和钢轨电位最小为目标,提出了多变流器双目标优化控制算法作为全局优化算法,应用于多变流器分层控制策略。该优化模型如式(3)~式(5)所示。

式中,t为当前的优化时刻;f1(X,t)、f2(X,t)为目标函数;X为各变流器优化参数向量;Pw(X,t)为t时刻全线网损;Urmax(X,t)为t时刻全线钢轨电位最大值。假设全线共N个牵引变电所,M辆列车,在第i个牵引变电所处,Uqi(X,t)为接触网压,V;Uri(X,t)为钢轨电位,V;Iqi(X,t)为该牵引所处变流器输入或输出的电流,A。在第j个列车处,Ulj(X,t)为接触网压,V;Urj(X,t)为钢轨电位,V;Ilj(X,t)为列车吸收或反馈的电流,A。
为避免传统的多目标优化算法将各目标加权处理的主观性,本文采用NSGA-II算法进行多变流器双目标优化控制,该算法的控制流程如图4所示。
如图4所示,在NSGA-II的优化过程中,对每一代解集进行非支配排序,从而得到多层子解集,并对每一层解集分配对应的个体等级、计算拥挤距离。在第k次进化迭代时,通过对解集Pk进行锦标赛选择,得到规模为S/2的父代,并通过交叉变异得到子代Qk,合并种群Pk、Qk后重新进行非支配排序、等级分配和拥挤距离计算。通过精英策略的选择与进化,解集中的优秀个体被有效地保留,最终得到帕累托解集PK。

图4 NSGA-II控制流程Figure 4 Flow chart of NSGA-II
根据NSGA-II所生成的帕累托解集,中央控制器可综合各优化目标,使用不同的判据来选取最终解,如隶属度函数、核密度估计等方法。为便于快速选取变流器参数,本文采用归一化欧式距离作为指标进行最终解的选取。在时刻t所得的帕累托解集PK中,第l个非支配解Xl所对应的归一化欧式距离dl(t)如式(6)所示。

式中,f1l(Xl,t)、f2l(Xl,t)为该时刻Xl所对应的目标函数值;Pw(t)、Urmax(t)分别为优化前该时刻全线网损和钢轨电位最大值。通过计算任意时刻下各非支配解所对应的归一化欧式距离,可以通过寻找距离最小值实现最终解的快速搜索。
3 仿真分析
3.1 仿真平台介绍
为对多变流器智能优化控制方法进行仿真分析,本文基于 MATLAB软件搭建了国内某地铁线路的仿真平台,该线路总长 13 697 m,共设有 5个牵引所(T1~T5)、13个车站(S1~S13),各车站及牵引所分布如图5所示。

图5 地铁线路示意图Figure 5 Diagram of subway line
本文设置仿真步长为1 s,线路上行、下行各列车发车间隔均为180 s,各列车在13个车站的停站时间均为30 s。首先,该仿真平台通过列车牵引计算得到各列车的位置及功率动态变化情况,且线路运行图以180 s为周期循环重复。结合牵引所参数、供电系统及回流系统阻抗等线路参数,仿真平台列写任意时刻的节点电压方程组,从而进行潮流计算迭代求解得到全线供电参数动态分布情况。
本文设置各变流器仿真参数如表1所示,优化前各变流器取值均相同且不随时间变化,采用基于GOOSE通信的多变流器智能优化控制方法时,各变流器参数将根据双目标优化控制算法实时调整。

表1 变流器仿真参数Table 1 Simulation parameters of converters
3.2 仿真结果分析
本文基于仿真平台模拟了全线变流器采用GOOSE通信时,多变流器智能优化控制方法下全线供电参数动态分布。图6以1 333 s为例,给出了该时刻下双目标优化控制算法所得到的帕累托解集。

图6 1 333 s双目标优化控制算法帕累托解集Figure 6 Pareto solution set of dual-objective optimization control algorithm at 1333 s
如图6所示,本文所提出的多变流器智能优化控制方法可将1 333 s时的全线网损控制在660 kW内,将该时刻钢轨电位控制在50 V内。而优化前,1 333 s时刻全线网损高达885.8 kW,全线钢轨电位幅值最大值为84.7 V。因此,本文所提出的多变流器智能优化控制方法能够大大降低全线能量损耗,并有效提升系统运行的安全性。图7给出了根据归一化欧式距离选取最终解进行优化时,对比优化前1 333 s全线钢轨电位的分布情况。

图7 1 333 s优化前后全线钢轨电位对比Figure 7 Comparison of rail potential at 1333 s before and after optimization
如图7所示,优化后1 333 s全线的钢轨电位与优化前相比,均呈现出不同程度的降低。此外,优化后1 333 s全线总网损为659.0 kW,比优化前降低了226.8 kW。因此,本文所提出的多变流器优化控制方法能够针对任意时刻线路状态进行变流器参数优化,从而有效抑制全线钢轨电位,大大提升系统安全性能。
基于该仿真平台,图8给出了采用多变流器智能优化控制方法时,1 300~1 480 s内双目标优化控制算法所得到的各时刻最终解集。图9给出了与优化前对比,采用该优化方法时全线网损及钢轨电位动态分布。为便于对比分析优化控制方法的效果,图9同时给出了优化前1 300~1 480 s内全线网损及钢轨电位最大值的动态分布。
如图8、9所示,本文所提出的基于GOOSE通信的多变流器优化控制方法能够综合抑制全线的网络损耗以及钢轨电位。如图9(a)所示,变流器参数优化前,1 300~1 480 s内全线网损最大值为1 307.0 kW,平均损耗为613.8 kW/s。而采用多变流器优化控制方法时,全线网损最大值为1 253.0 kW,与优化前相比降低了54.0 kW;平均网损为504.6 kW/s,与优化前相比降低了109.2 kW。

图8 1 300~1 480 s双目标优化控制算法最终解集Figure 8 The final solution set of the dual-objective optimization control algorithm from 1300 s to 1480 s

图9 变流器参数优化后全线网损及钢轨电位动态分布Figure 9 Dynamic distribution of the power loss and rail potential after the optimization of the converter parameters
如图9(b)所示,优化前该时段内全线钢轨电位幅值最大值为94.9 V。对照国家标准GB 50490-2016中所规定的“正线回流轨与地之间的电压不应超过 DC 90 V”,优化前线路钢轨电位超过限值,威胁着设备和人员的安全。而优化后全线钢轨电位幅值最大值仅为47.6 V,比优化前降低了47.3 V,且远低于标准所规定的限值90 V。
因此,使用本文所提出的多变流器智能优化控制方法,能够通过GOOSE通信网损对各变流器参数进行实时调控,并基于双目标优化算法准确调控各变流器参数,从而有效降低系统损耗和钢轨电位,实现线路节能、安全运行。
此外,图10给出了传统的地铁牵引供电系统中,即各变流器间无通信网络时,以1 300~1 480 s内各时刻网损最大值以及钢轨电位幅值最大值为优化目标,同样采用基于NSGA-II的双目标优化控制算法时,针对各变流器参数进行无通信优化所得的帕累托解集。

图10 1 300~1 480 s无通信优化算法帕累托解集Figure 10 Pareto solution set of no communication optimization algorithm from 1300 s to 1480 s
根据图10所给出的无通信优化的帕累托解集,本文同样通过比较归一化欧式距离选取了最终解,得到在1 300~1 480 s内采用无通信优化算法时,全线网损和钢轨电位动态分布如图11所示。
如图11(a)所示,采用无通信优化时全线网损最大值为1 060 kW,与采用GOOSE通信优化时相比略有降低。如图11(b)所示,采用无通信优化时全线钢轨电位幅值最大值为50.4 V,且各时刻下钢轨电位最大值均高于采用GOOSE通信优化时的幅值。然而,尽管无通信优化同样能够达到降低系统网损和钢轨电位的目的,这一优化方法却要求线路运行图保持一致,当列车停站时间、限制速度等运行状况发生改变时,无通信优化无法实现动态调整。而本文所提出的基于GOOSE通信的多变流器智能优化控制方法则很好地解决了以上问题,能够针对当前时刻运行状态实时调整各变流器参数,具有较好的适应性。
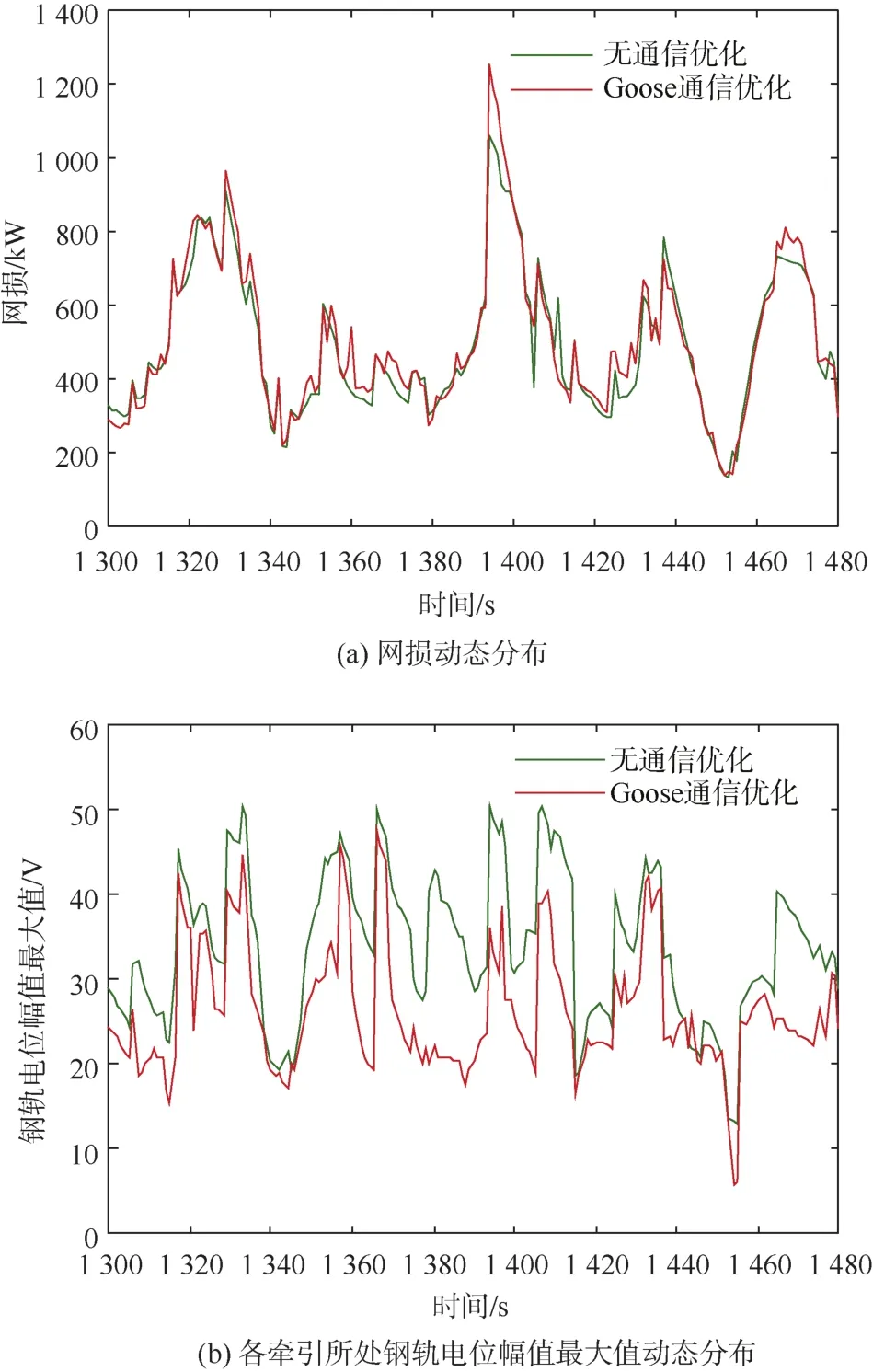
图11 变流器参数无通信优化时全线网损及钢轨电位动态分布Figure 11 Dynamic distribution of the power loss and rail potential after the no communication optimization
4 结语
针对地铁各变流器独立运行、缺乏信息互通、无法协调控制等问题,本文提出了一种基于GOOSE通信的地铁多变流器智能优化控制方法。为实现多变流器分层控制策略,本文以系统网络损耗最小和钢轨电位最小为目标,提出了基于NSGA-II算法的多变流器双目标优化控制算法。基于国内某实际线路的数据搭建了动态仿真平台,分析结果表明,本文所提出的地铁多变流器智能优化控制方法可通过各变流器输出特性的动态优化,降低全线的网络损耗以及钢轨电位。与传统的各变流器独立运行、变流器无通信优化控制相比,该智能优化控制方法能够实现变流器参数的实时、准确调控,有利于地铁线路的节能、安全运行。
